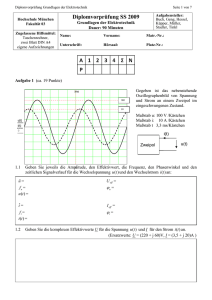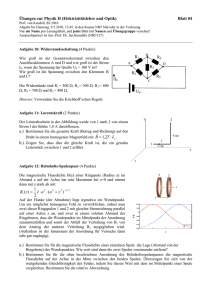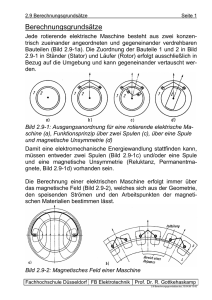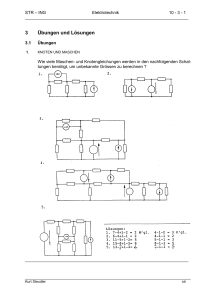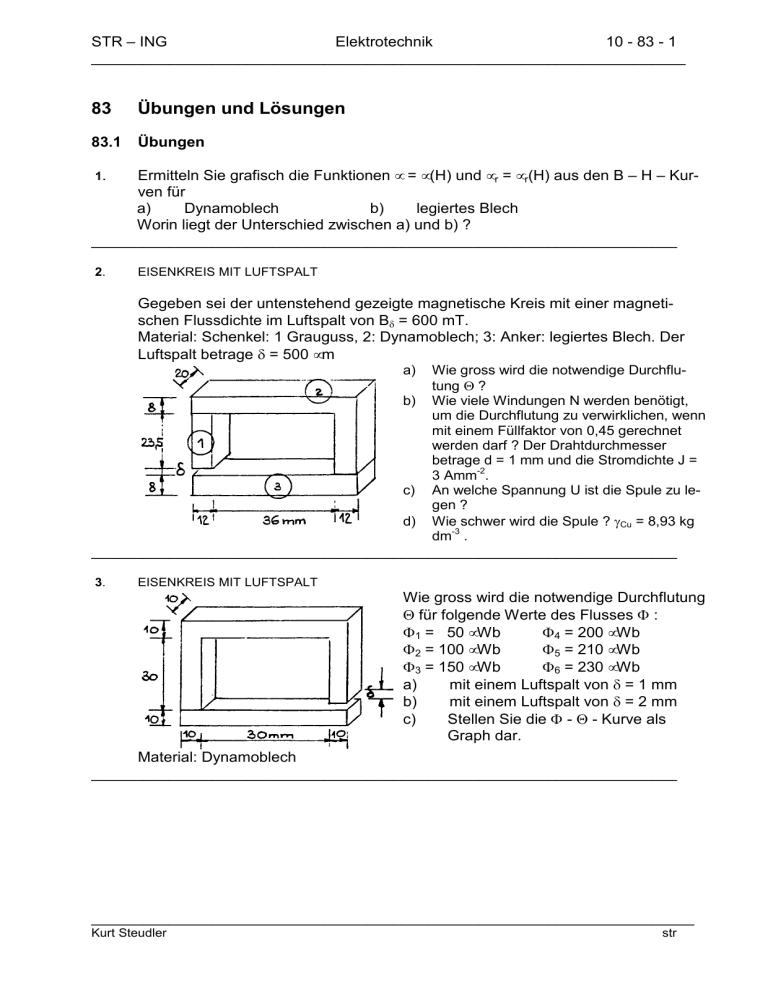
STR – ING Elektrotechnik 10 - 83 - 1 _____________________________________________________________________ 83 Übungen und Lösungen 83.1 Übungen Ermitteln Sie grafisch die Funktionen µ = µ(H) und µr = µr(H) aus den B – H – Kurven für a) Dynamoblech b) legiertes Blech Worin liegt der Unterschied zwischen a) und b) ? ____________________________________________________________________ 1. 2. EISENKREIS MIT LUFTSPALT Gegeben sei der untenstehend gezeigte magnetische Kreis mit einer magnetischen Flussdichte im Luftspalt von Bδ = 600 mT. Material: Schenkel: 1 Grauguss, 2: Dynamoblech; 3: Anker: legiertes Blech. Der Luftspalt betrage δ = 500 µm a) b) c) d) Wie gross wird die notwendige Durchflutung Θ ? Wie viele Windungen N werden benötigt, um die Durchflutung zu verwirklichen, wenn mit einem Füllfaktor von 0,45 gerechnet werden darf ? Der Drahtdurchmesser betrage d = 1 mm und die Stromdichte J = 3 Amm-2. An welche Spannung U ist die Spule zu legen ? Wie schwer wird die Spule ? γCu = 8,93 kg dm-3 . ____________________________________________________________________ 3. EISENKREIS MIT LUFTSPALT Wie gross wird die notwendige Durchflutung Θ für folgende Werte des Flusses Φ : Φ1 = 50 µWb Φ4 = 200 µWb Φ2 = 100 µWb Φ5 = 210 µWb Φ3 = 150 µWb Φ6 = 230 µWb a) mit einem Luftspalt von δ = 1 mm b) mit einem Luftspalt von δ = 2 mm c) Stellen Sie die Φ - Θ - Kurve als Graph dar. Material: Dynamoblech ____________________________________________________________________ ______________________________________________________________________ Kurt Steudler str STR – ING Elektrotechnik 10 - 83 - 2 _____________________________________________________________________ 4. EISENKREIS MIT LUFTSPALT Für die Ablenkung eines Elektronenstrahls im Luftspalt δ = 5 mm sei die nebenstehende Anordnung gegeben. Material: Weicheisen (Dynamoblech). Gefordert wird im Luftspalt eine magnetische Flussdichte von Bδ = 1,5 T. a) Wie gross wird die magnetische Durchflutung Θ ? b) Lässt sich die Spule verwirklichen mit J < 4 Amm-2 und einem Füllfaktor von k = 0,35 ? ____________________________________________________________________ 5. KREISRING MIT EISENKERN Ein Kreisring aus legiertem Blech sei eng gewickelt mit Draht vom Radius ρ = 300 µm. Die Stromdichte betrage J = 3 Amm-2. Der Durchmesser des Rings betrage D = 50 mm und jener einer einzelnen Windung d = 15 mm. a) Wie gross werden die magn. Flussdichte BFe und der Fluss ΦFe im geschlossenen Kreis ? b) Im Ring werde ein Luftspalt von δ = 1 mm vorgesehen. Welchen Wert nimmt Bδ an ? (Lösung durch Näherung). c) Im Luftspalt herrsche eine Flussdichte von Bδ = 300 mT. Wie gross wird die Durchflutung Θ ? ____________________________________________________________________ 6. EISENKREIS MIT DAUERMAGNET Im Luftspalt δ herrsche eine magnetische Flussdichte von Bδ = 1 T. Die notwendige Durchflutung Θ soll aus einem Dauermagneten erzeugt werden. Welches permanentmagnetische Material ist zu wählen ? Material: 1: Dynamoblech, 2: Dauermagnet, 3: legiertes Blech. ____________________________________________________________________ ______________________________________________________________________ Kurt Steudler str STR – ING Elektrotechnik 10 - 83 - 3 _____________________________________________________________________ 7. EISENKREIS MIT LUFTSPALT Im Luftspalt = 500 m wird eine magn. Flussdichte von B = 1,2 T gefordert. Material: Joch und Schenkel: Dynamoblech, Anker: legiertes Blech. Welche Durchflutung Θ muss um den Mittelschenkel erzeugt werden ? Verwirklichen Sie die optimale Wicklung (Wickelraum möglichst voll nutzen). ____________________________________________________________________ 8. EISENKREIS MIT LUFTSPALT Im Luftspalt δ soll eine magnetische Flussdichte von Bδ = 900 mT herrschen. Wie gross wird die notwendige Durchflutung Θ? Material: Weg li Ai Bi 2 [A]=mm [B] = T li Hi -1 [H]=kAm [l]= mm 1: Dynamoblech 2: legiertes Blech Θ Bemerkungen (Material) [Θ] = A ____________________________________________________________________ ______________________________________________________________________ Kurt Steudler str STR – ING Elektrotechnik 10 - 83 - 4 _____________________________________________________________________ Weg li Weg li Ai Bi 2 [A]=mm Ai [B] = T Bi 2 [A]=mm [B] = T li Hi [H]=kAm-1 [l]= mm li Hi -1 [H]=kAm [l]= mm Θ Bemerkungen (Material) [Θ] = A Θ Bemerkungen (Material) [Θ] = A ______________________________________________________________________ Kurt Steudler str STR – ING Elektrotechnik 10 - 83 - 5 _____________________________________________________________________ Weg li Weg li Ai Bi 2 [A]=mm Ai [B] = T Bi 2 [A]=mm [B] = T li Hi [H]=kAm-1 [l]= mm li Hi -1 [H]=kAm [l]= mm Θ Bemerkungen (Material) [Θ] = A Θ Bemerkungen (Material) [Θ] = A ______________________________________________________________________ Kurt Steudler str STR – ING Elektrotechnik 10 - 83 - 6 _____________________________________________________________________ 83.2 Lösungen 6. ______________________________________________________________________ Kurt Steudler str STR – ING Elektrotechnik 10 - 83 - 7 _____________________________________________________________________ 7. ______________________________________________________________________ Kurt Steudler str