Übersicht Begriffe und Aufgabentypen

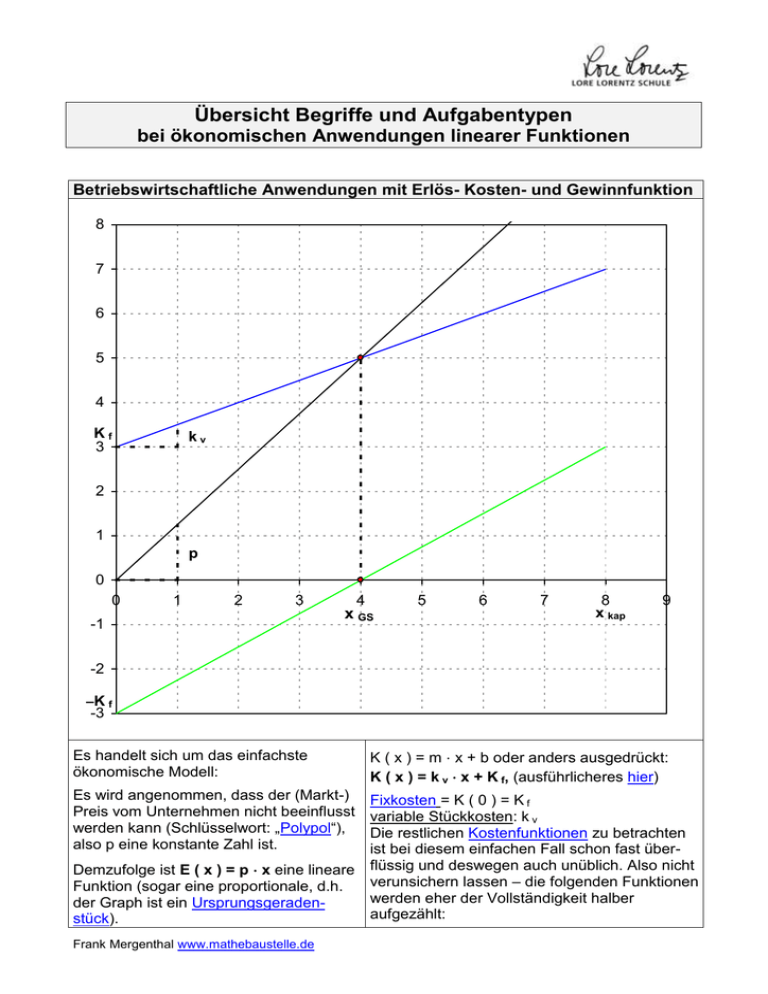
Übersicht Begriffe und Aufgabentypen
bei ökonomischen Anwendungen linearer Funktionen
Betriebswirtschaftliche Anwendungen mit Erlös- Kosten- und Gewinnfunktion
8
7
6
5
4
Kf
3
kv
2
1
p
0
0
1
2
3
-1
4
x GS
5
6
7
8
x kap
9
-2
–K f
-3
Es handelt sich um das einfachste
ökonomische Modell:
Es wird angenommen, dass der (Markt-)
Preis vom Unternehmen nicht beeinflusst
werden kann (Schlüsselwort: „Polypol“),
also p eine konstante Zahl ist.
K ( x ) = m  x + b oder anders ausgedrückt:
K ( x ) = k v  x + K f, (ausführlicheres hier)
Fixkosten = K ( 0 ) = K f
variable Stückkosten: k v
Die restlichen Kostenfunktionen zu betrachten
ist bei diesem einfachen Fall schon fast überDemzufolge ist E ( x ) = p  x eine lineare flüssig und deswegen auch unüblich. Also nicht
verunsichern lassen – die folgenden Funktionen
Funktion (sogar eine proportionale, d.h.
werden eher der Vollständigkeit halber
der Graph ist ein Ursprungsgeradenaufgezählt:
stück).
Frank Mergenthal www.mathebaustelle.de
Wenn man das zum ersten Mal sieht,
variable (Gesamt-)Kostenfunktion:
Die Kosten setzen folgendermaßen
zusammen:
Kv( x ) = K ( x ) – Kf = kv  x
Stückkostenfunktion:
k( x ) =
K
K(x)
= kv + f
x
x
Die variable Stückkostenfunktion ist konstant
k v ( x ) = k v IR
Grenzkostenfunktion:
K ´( x ) = k v
(k v ist schließlich die Steigung von K)
ökonomischer Definitionsbereich ( D ök )
im Fall eines Polypols
Erlösfunktion aufstellen (p gegeben)
D ök = [ 0 ; x kap ], wobei x kap die
Kapazitätsgrenze ist
E(x)=px
Eigenschaften: geht durch den Ursprung, steigt
(also p>0)
Gewinnfunktion aufstellen
(wenn E und K gegeben)
G(x)=E(x)–K(x)
= ( p – kv )  x – Kf
Achtung: Klammern setzen!
Eigenschaften: schneidet die y-Achse , steigt (also
p>0)
Gewinnschwelle (x GS, Nullstelle von G
bzw. Schnittstelle von E und K)
G(x)=0
(oder: E ( x ) = K ( x ))
Lösung der linearen Gleichung
Gewinnzone
G ( x ) = 0 (s.o.);
Die Gewinnzone ist [ x GS ; x kap ]
gewinnmaximale Ausbringungsmenge
( x Gmax ) und maximalen Gewinn
berechnen
Ein möglichst großer Gewinn wird durch eine
möglichst große Ausbringungsmenge erzielt,
also gilt:
x Gmax = x kap.
maximaler Gewinn: G ( x kap )
Kosten berechnen (bzw. Erlös oder
Gewinn/Verlust) bei gegebener
Ausbringungsmenge von x 0 ME
Einsetzen von x 0 in die entsprechende
Funktion:
K ( x0 )
(bzw. E ( x 0 ) oder G ( x 0 ))
Ausbringungsmenge berechnen bei
gegebenen Kosten (bzw. Erlös oder
Gewinn/Verlust) Erlös oder
Gewinn/Verlust) von y 0 GE(/ME)
K ( x ) = y 0 lösen
(bzw. E ( x ) = y 0 oder G ( x ) = y 0 )
Lösung der linearen Gleichung
Übungen Erlös-, Kosten und Gewinnfunktionen
Frank Mergenthal www.mathebaustelle.de
Betriebswirtschaftliche Anwendungen mit zwei verschiedenen
Kostenfunktionen
kritische Produktionsmenge.
(Schnittstelle zweier Kostenfunktionen.
Ab dieser Produktionsmenge ist das eine
Produktionsverfahren kostengünstiger als
das andere.)
Gegeben: K 1 ( x ) = m 1x + b 1 und
K 2 ( x ) = m 2x + b 2
K1(x)=K2(x)
Lösung der linearen Gleichung
Lineare Abschreibung
Grundformel:
R ( n ) = Restbuchwert nach n Jahren
A = Anschaffungspreis
a = jährlicher Abschreibungsbetrag
R ( n ) = A – a  n.
n = seit Abschreibungsbeginn
vergangene Zeit in Jahren
Gesamtdauer der Abschreibung
R(n)=0
A–an=0
Auflösung der linearen Gleichung nach n
Restbuchwert nach n Jahren
Einsetzen:
R(n)=A–an
Dauer, bis der Restbuchwert y 0 erreicht
ist
R ( n ) = y0
 A – a  n = y0
Auflösung der linearen Gleichung nach n
Bestimmung des Abschreibungsbetrage
so, dass eine Anschaffung nach n 0
Jahren abgeschrieben ist.
R(n)=0
 A – a  n0 = 0
Auflösung der linearen Gleichung nach a.
Volkswirtschaftliche Anwendungen: Marktpreisbildung
p N: lineare Preisnachfragefunktion,
fällt immer.
Bedeutung: p N ( x 0 ) = y 0 bedeutet: Bei
einem Preis von y 0 GE/ME werden x 0
ME nachgefragt. (Wenn jeder Käufer nur
ein Produkt kauft und eine ME ein Stück
ist, heißt das: x 0 Interessenten sind
bereit, das Produkt zu diesem Preis
zukaufen.)
b N ist dabei der höchste erzielbare (also
maximale) Preis (der keinem etwas nützt,
weil zu ihm keine Mengeneinheit verkauft
werden kann).
Der Betrag von m N gibt an, um wie viel
der Preis fallen muss, damit eine ME
mehr nachgefragt wird.
Frank Mergenthal www.mathebaustelle.de
p N ( x ) = m Nx + b N , wobei m N < 0, b N > 0
p A: lineare Preisangebotsfunktion,
p A ( x ) = m Ax + b A , wobei m A > 0
steigt immer.
Bedeutung: p A ( x 0 ) = y 0 bedeutet: Bei
einem Preis von y 0 GE/ME werden x 0
ME angeboten.
Der Betrag von m A gibt an, um wie viel
der Preis steigen muss, damit eine ME
mehr angeboten wird.
Marktgleichgewicht,
Gleichgewichtsmenge,
Gleichgewichtspreis
pA ( x ) = pN ( x )
Lösen der linearen Gleichung.
Berechnung von Nachfrage- bzw.
Angebotsüberhang bei vorgegebenem
Preis p = c
pA ( x ) = p
Lösen der linearen Gleichung. Man erhält die
zu diesem Preis angebotene Menge.
Die Schnittstelle x S ist die
Gleichgewichtsmenge, der zugehörige
Funktionswert p A ( x S ) ist der
Gleichgewichtspreis, der zugehörige Punkt
( x S  p A ( x S ) ist das Marktgleichgewicht.
pN ( x ) = p
Lösen der linearen Gleichung. Man erhält die
zu diesem Preis nachgefragte Menge.
Eine der beiden Menge ist größer, wenn nicht
ausgerechnet eine Marktgleichgewicht vorliegt.
Die Differenz ist der entsprechende Überhang.
Links zu ökonomischen Funktionen: hier
Frank Mergenthal www.mathebaustelle.de