Y r - Semestra
Werbung

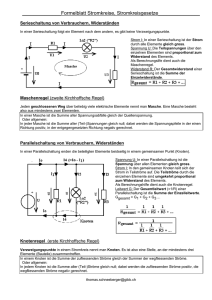
Weitere Files findest du auf www.semestra.ch/files DIE FILES DÜRFEN NUR FÜR DEN EIGENEN GEBRAUCH BENUTZT WERDEN. DAS COPYRIGHT LIEGT BEIM JEWEILIGEN AUTOR. Zusammenfassung Netzwerke und Schaltungen I Energie 1 Q r E= 4 0 r 2 r W 12=Q ∫ E ds = F Eq Michael Müri U 12=∫ E ds U 12=E 12 /Q Verbraucherzählpfeilsystem Spannungspfeil von + nach – hat einen positiven Zahlenwert. Verbraucher erhält Energie. (offizielle Konvention in der Elektrotechnik) Widerstand R/ Leitwert G / Stromdichte S R=l / A G=1/ R S= I / A (A=Kontrollfläche) =20 [1−20] (Tabelle siehe Skript S.34) =1/ (el. Leitfähigkeit) −8 −8 Al=2.7⋅10 Einige Werte: Cu =1.7⋅10 Rückleitung berücksichtigen! Bei einem Spannungsteiler (siehe Rechts) beträgt der Innenwiderstand bzgl. Ue :=0 des Ausgangs Ua Ri = R2∥R1 Spannung/Strom I =dQ /dt (Stromrichtung = Richtung der positiven Ionen) Spannungsquellen dürfen nicht parallel, (ideale) Stromquellen nicht in Serie geschaltet werden! Eine Stromquelle muss immer eine Mindestbelastung haben ( U ∞ ), Kurzschluss möglich (U=0) Quellenumwandlung I + paralleler Widerstand = U + serieller Widerstand Spannungsteiler Ui Ri = unbelastet: U tot R1R 2 belastet: I q=−U q / Ri U 2' R2 ' = U tot R1R 2 ' ( R2 ' =R 2∥R Last ) S.62 Leistung/Arbeit P=dW /dt=U I =R I 2 Reale Spannungsquelle: Wirkungsgrad: = P nutz P gesamt Max. Leistung an Last: Ri= R L Leistung der idealen Spannungsquelle= P 0=P i P L Linearisierung/Ersatzschaltung Ersatzschema eines linearisierten Kurvenabschnitts U I =U q I Ri (Ersatzwiderstand kann auch negativ sein) Diode Shockley-Modell: I D =I S e U De ' −1 kT (S=Sperr, D=Durchlass, k=1.3807*10-23VAs/K, e'=1.6022*10-19As, T=Temperatur) U D/ U T andere Darstellung: I D =I S e −1 ZENER-Diode (S.75): ab einer bestimmten Spannung UZ0 in Sperrrichtung wird die Diode leitend. (Ersatzschaltbild: siehe Linearisierung, R Z = [email protected] U Z I Z max−U z0 ) I Z max V 1.4 1/7 Zusammenfassung Netzwerke und Schaltungen I Michael Müri Bsp: Schutz vor falscher Polarität: Metalloxid-Ableiter (Varistor) spannungsabhäniger Widerstand (ähnlich ZENER-Diode, allerdings im 0-Punkt symmetrisch) Bipolartransistor I C =B I B I E = B1 I B Ersatzschaltbild & Beispiele siehe S.81-83 Ersatzschaltbild: RB Ist Uearly gross, so gilt GC E=0 uT Kondensator Strom: I C =C U˙ C B*IB 2 Energie: W C =1/ 2C U C U C = AB e−t / RC I C =D e −t / RC Ladung: Q=C U C t=0 ⇒U C =A B⇔ I C =D =R C t=∞ ⇒U C = A⇔ I C =0 I =I 1= I 2=...=I n , U =U 1U 2...U n , 1/C=1/C 1...1/C n I =I 1 I 2 ...I n , U =U 1=U 2=...=U n , C=C 1 C 2...C n Serieschaltung: Parallelschaltung: Bei Umladungen mit Q=CU=c rechnen! Beim CRC-Kreis hängt die verlorene Energie nicht von R ab! U C =U C ∞U C 0−U C ∞e U C ∞−U C 0 −t / I C =C⋅ e −t / Zeitkonstante: R aus Sicht des Kondensators/Spule zusammenfassen! T=RC Spule Spannung: U L= L I˙L −t R/ L I L = AB e Serieschaltung: Parallelschaltung: 2 Energie: W L=1 /2 L I L −t R / L U L= D e t=0 ⇒ I L= AB ⇔U L =D =L / R t=∞ ⇒ I L = A⇔U L =0 I =I 1= I 2=...=I n , U =U 1U 2...U n , L=L1 L2...L n I =I 1 I 2 ...I n , U =U 1=U 2=...=U n , 1/ L=1/ L1...1/ Ln Ein Ladevorgang gilt als abgeschlossen, wenn der Fehler < 1% ist. 2 W L I L (t ist die Zeit, zu der der Vorgang als abgeschlossen gilt) Momentanleistung: p= = t 2t [email protected] V 1.4 2/7 Zusammenfassung Netzwerke und Schaltungen I Michael Müri RL-Kreis Uq-UL-UR=0 I L= → Uq −t / 1e (Lösung der inhomogenen Diff-Gl. siehe S.98ff) R Operationsverstärker (OpAmp) I e=0 v=∞ U e =0 UA R2 Invertierer: U =− R E 1 Ue UE UA Addierer: U A=−R2 ∑ Nichtinvertierender OpAmp Ui Ri Spannungsfolger: UA=UE (S.108) Differenzverstärker: U A= R2 U −U E1 R1 E2 Es muss gelten R1=R3 und R2=R4 UE1 UE2 Integrierer: U A=− 1 ∫ U E U A0 CR (UA0=Anfangsspannung des Kondensators) Differenzierer: U a=−C R U̇ e [email protected] V 1.4 3/7 Zusammenfassung Netzwerke und Schaltungen I Michael Müri Netzwerke Graph: Baum: (keine Maschen) Äste Sehnen z B=k −1 s=m= z−z B Netzwerkanalyse Maschenstromverfahren 1. Quellenumwandlung Alle Strom- in Spannungsquellen umwandeln 2. Baum festlegen Baum, Äste & Sehnen definieren Maschen = Sehnen = Zweige – Knoten + 1 Äste = Zweige - Sehnen 3. Zweige definieren Zweige nummerieren & Stromrichtung festlegen Umlaufrichtung einer Masche = Stromrichtung in der Sehne 4. Zweigimpedanzmatrix Zz Diagonalmatrix mit Widerständen aller Zweige 5. Zweig-Sehnen-Inzidenzmatrix A Ströme durch Maschenströme (Bsp: I1, I5) ausdrücken Bsp: [ ] [ ][ ] I1 1 0 I I2 −1 1 = ∗ 1 ... ... I5 ... ... ... In 6. Maschenimpedanzmatrix Zm Zm=AT*Zz*A 7. eingeprägte Maschenspannungen Uqm Uqm=-AT*Uqz Zweigspannungsquellen Uqz [ ][ ] U q1 U q1 0 0 = Bsp: U q z= U q3 −I 1∗R4 −U q2 −U q2 8. Maschenströme Im Zm*Im=Uqm Im=Zm-1*Uqm 9. Zweigströme Iz Iz=A*Im 10. Zweigspannungen UZ total UZ total=ZzIz+Uqz [email protected] V 1.4 [ U qm= U q1 U q2 I 1∗R4 ] 4/7 Zusammenfassung Netzwerke und Schaltungen I Michael Müri Knotenpotentialverfahren Netzwerk enthält nur spannungsgesteuerte Quellen 1. Quellenumwandlung Alle Spannungs- in Stromquellen umwandeln 2. gerichteter Graph 0-Knoten definieren, Quellen weglassen, Zweige nummerieren 3. Admittanzmatrix G Diagonalmatrix mit Leitwerten (Gn=1/Rn) der Zweige 4. Zweigknoteninzidenzmatrix A Zweige & zugehörige Knoten (ohne Referenz 0) [ 1 Bsp: A= −1 0 0 0 −1 0 1 0 0 1 −1 1 0 0 ] Zweig 1: Knoten 1-2 Zweig 2: Knoten 2-3 Zweig 3: Knoten 3-0 ... 5. Knotenadmittanzmatrix Y Y=A*G*AT [ G 1G 4 −G1 0 G1 G 2G 5 −G 2 Bsp: Y = −G 1 0 −G 2 G 2G 3 6. Knotenpotentiale V ] V=Knotenpotentiale, Ikq = Knotenströme von Quellen Bsp: positiv: in den Knoten I q4 hineingehend I kq= I q 3U q 2 / R2 Achtung: U / R =−I q2 2 q2 [ I kq=Y V ] ⇒ V =Y −1 I kq kommt eine ideale Stromquelle vor, kann ein paralleler Widerstand R eingeführt werden. Wenn Y aufgestellt wurde, lässt man R → ∞ (e.g. G → 0) und erhält so das Resultat. Kurzes Knotenpotentialverfahren Direktes Aufstellen der Knotenadmittanzmatrix Y: • • Die Hauptdiagonalelemente y i i sind die Summe der am Knoten i angeschlossenen Leitwerte Jedes Nicht-Diagonal-Element y i k ist der negative Leitwert zwischen den beiden Knoten i und k [email protected] V 1.4 5/7 Zusammenfassung Netzwerke und Schaltungen I Michael Müri Erweitertes Knotenpotentialverfahren Netzwerk enthält auch nicht-spannungsgesteuerte Quellen, BJT's, etc. Yr C B V I ⋅ = kq D Ie e T Y r =Ar G Ar Ar enthält nur resistive Zweige B enthält alle Ströme mit anderen Strom-Spannungsbeziehungen C enthält Beziehungen zwischen Knotenpotentialen V und Quellenspannungen e D enthält alle restlichen Beziehungen Ie enthält gesteuerte und unbestimmte Ströme Ikq ist der Stromquellenvektor e ist der Spannungsquellenvektor zwischen 2 Knoten befindet sich immer ein Netzwerkelement Bsp: Schaltung mit einem BJT-Transistor resistive Zweige: Zweig 5&6 enthalten ideale Spannungsquellen (Strom einführen), I 7=K⋅I 6 I 1 =G 1 V 1 I 3=G 3 V 3−G 3 V 2 Matrixschreibweise: I 2=G 2 V 2 I 4=G 4 V 3−G 4 V 4 G1 0 0 0 0 G 2G 3 −G 3 0 0 −G 3 G 3G 4 −G 4 0 0 −G 4 G4 Y r zusätzliche GL: V 3=U q5 V1 V2 0 −1 −1 0 V3 0 1 0 0 ⋅ V4 = 0 1 0 0 I5 0 0 0 1 I6 I7 B −V 1V 2=U q6 ⋅ V Ströme in Knoten 1 Ströme in Knoten 2 T I e = I kq K I 6−I 7=0 U q5 0 0 1 0 0 0 0 V = U q6 −1 1 0 0 0 0 0 ⋅ Ie 0 0 0 0 0 K −1 0 Gleichungssystem: [email protected] C D ⋅ V G1 0 0 0 0 G 2G 3 −G 3 0 0 −G 3 G3 G 4 −G 4 0 0 −G 4 G4 0 0 1 0 −1 1 0 0 0 0 0 0 V 1.4 T I e =e 0 −1 −1 0 1 0 1 0 0 0 0 1 ⋅ 0 0 0 0 0 0 0 K −1 V1 0 V2 0 V3 0 V4 = 0 U q5 I5 U q6 I6 0 I7 6/7 Zusammenfassung Netzwerke und Schaltungen I Michael Müri Schwingkreis U =U LU C U R → C u̇=LC ïRC i̇i die partikuläre Lösung ist abhängig von u(t) homogene Lösung: 1 , 2= det(chp(λ)) > 0 → det(chp(λ)) = 0 → det(chp(λ)) < 0 → −R R 2 1 ± − 2L 2L LC t t it =A e B e t it = AB t e − D t it = Acos t B sin t e 1 2 0 Allgemeines Vorgehen bei der Berechnung eines Schwingkreises 1. 2. 3. 4. Aufstellen der Elementgleichungen für jedes Element im Netzwerk Maschen- & Knotengleichungen aufstellen Aufstellen der Differentialgleichungen (Substitutionen durchführen) Lösen der Differentialgleichung (homogene Lösung, partikuläre Lösung, Anfangsbedingungen) [email protected] V 1.4 7/7