Mathematik_12_files/Darstellung Exp

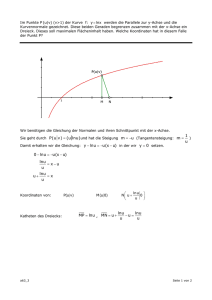
École Internationale Allemande
Einheitliche Darstellung von Exponentialfunktionen
Bei allen Funktionstypen haben wir uns auf eine Form verabredet, damit man besser
Vergleichen kann oder die Koeffizienten immer auf die gleiche Weise angeben kann.
Bei Polynomen (ganzrationale Funktionen) ordnen wir nach Potenzen:
Beispiel:
f (x) = 3x 4 −2x 3 + 0,5x 2 − x + 2
allgemein:
f (x) = an x n + an−1 x n−1 +…+ a1 x + a0 = ∑ ai x i
n
i=0
an heißen Koeffizienten
Spezialfälle waren die lineare Funktion, genormt auf:
Gerade:
g(x) = mx + c
m heißt Steigung, c verschiebt entlang y
und die quadratische Funktion schreiben wir einheitlich:
Parabel:
p(x) = ax 2 + bx + c
Exponentialfunktion
Alle Exponentialfunktionen lassen sich mit der Basis e und zwei Koeffizienten darstellen:
exponentiell
f (x) = aebx
a ist der Anfangswert, b bestimmt die Basis, a,b ∈ 
Satz
Jede Exponentialfunktion mit reeller positiver Basis lässt sich in der oben gezeigten Form
(ln z )⋅x
x
; b = ln z
darstellen. a ⋅ z = a ⋅e
Aufgaben
n
1. Wie lässt sich die Zahl 2 in der Form e darstellen. Bestimme n so, dass 2 herauskommt!
2. Wie lautet die Funktion f (x) = 2 x in genormter Darstellung? Wie lauten a und b?
3. Beweise oben stehenden Satz.
4. Schreibe in Normdarstellung: f4 (t) =120 ⋅0,1t (Ergebnis: f4 (x) =120 ⋅e−t ln10
5. Schreibe in Normsdarstellung und vereinfache den Logarithmus soweit wie möglich:
f5 (t) = 345⋅( 41 )
t
f6 (t) = 0,2 ⋅( 45 )
t
nur natürliche Zahlen im ln
Kleiner Tipp für die Aufgaben: ebx = (eb ) ; elnu = u ; ln(eu ) = u
x
Logarithmusgesetze
ln
uv ) = v ⋅lnu
(

Exponent vorziehen
ln
uv ) = lnu + lnv
(

Additionsgesetz
ln( uv ) = ln(uv −1 ) = lnu + lnv −1 = lnu −lnv

Subtraktionsgesetz (abgeleitet von den ersten beiden Gesetzen)
1/2
École Internationale Allemande
Lö
su
Einheitliche Darstellung von Exponentialfunktionen
ng
Satz
Jede Exponentialfunktion mit reeller positiver Basis lässt sich in der oben gezeigten Form
(ln z )⋅x
x
; b = ln z
darstellen. a ⋅ z = a ⋅e
Aufgaben
n
1. Wie lässt sich die Zahl 2 in der Form e darstellen. Bestimme n so, dass 2 herauskommt!
en = 2 | ln
lnen = ln2
n = ln2
2. Wie lautet die Funktion f (x) = 2 x in genormter Darstellung? Wie lauten a und b?
f (x) = 2 x = (eln2 ) =1⋅e ln2 ⋅x
a =1; b = ln2
x
(
)
3. Beweise oben stehenden Satz.
a ⋅ z x = a ⋅(eln z ) = a ⋅e ln z ⋅x
Da z > 0, ist b = ln z möglich.
x
(
)
4. Schreibe in Normdarstellung:
(
f4 (t) =120 ⋅0,1t =120 ⋅e(ln0,1)⋅x =120 ⋅e ln10
−1
)⋅x
(
)
=120 ⋅e− ln10 ⋅x =120e−x ln10
5. Schreibe in Normsdarstellung und vereinfache den Logarithmus soweit wie möglich:
f (t) = 345⋅( ) = 345⋅(e ) = 345⋅e
1
4
5
345⋅e
⎛ 1⎞
t ln⎜⎜⎜ ⎟⎟⎟
⎝4⎠
⎛⎜ 1 ⎞⎟ t
⎜⎜ln ⎟⎟
⎝ 4⎠
t
(
⎛ 1⎞
t ln⎜⎜⎜ ⎟⎟⎟
⎝4⎠
(
−1
)
= 345⋅et ln 4 = 345e−t ln4
)
= 345et ln1−ln4 = 345e−t ln4
f6 (t) = 0,2⋅(
5
4
)
t
= 0,2⋅e
⎛ 5⎞
t ln⎜⎜⎜ ⎟⎟⎟
⎝4⎠
(
−1
)
(
= 0,2et ln5⋅4 = 0,2et ln5−ln4
)
2/2