1 u 0 − lnu = −u(x − u) lnu u = x − u u + lnu u = x MP - SOS

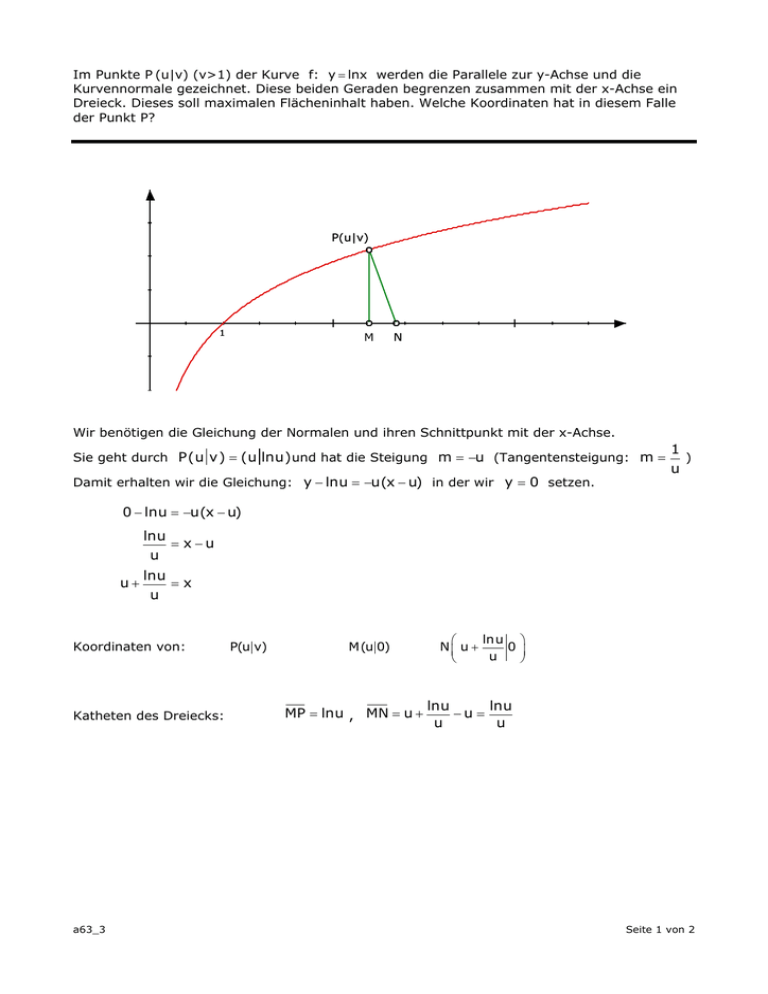
Im Punkte P (u|v) (v>1) der Kurve f: y = lnx werden die Parallele zur y-Achse und die
Kurvennormale gezeichnet. Diese beiden Geraden begrenzen zusammen mit der x-Achse ein
Dreieck. Dieses soll maximalen Flächeninhalt haben. Welche Koordinaten hat in diesem Falle
der Punkt P?
gsave currentpoint translate stroke 1 4 div setlinewidth
0 setgray 194.079
215.000 128.000 2.
P(u|v)
1
M
N
Wir benötigen die Gleichung der Normalen und ihren Schnittpunkt mit der x-Achse.
Sie geht durch P(u v) = (u lnu) und hat die Steigung m = −u (Tangentensteigung: m =
Damit erhalten wir die Gleichung: y − lnu = −u(x − u) in der wir y = 0 setzen.
1
)
u
0 − lnu = −u(x − u)
lnu
= x−u
u
u+
lnu
=x
u
Koordinaten von:
Katheten des Dreiecks:
a63_3
P(u v)
M(u 0)
MP = lnu , MN = u +
lnu ⎞
⎛
N⎜ u +
0⎟
u
⎝
⎠
lnu
lnu
−u =
u
u
Seite 1 von 2
Fläche des Dreiecks:
A=
(lnu)2
1 lnu
⋅
⋅ lnu =
2u
2 u
2lnu ⋅
A′ =
1
⋅ 2u − 2 ⋅ (lnu)2
u
=0
4u2
2lnu ⋅
1
⋅ 2u − 2 ⋅ (lnu)2 = 0
u
4lnu − 2(lnu)2 = 0
2lnu ⋅ (2 − lnu) = 0
lnu = 0
u=1
Minimum
lnu = 2
u = e2
v=2
(
Dreiecksfläche maximal für P e
a63_3
Maximum
2
2
)
Seite 2 von 2