Klausur 4 - Volker Bock

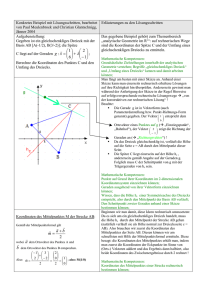
Klausur 4
Francisceum Zerbst
Arbeitszeit: 180 min
1.Leistungskurs Mathematik
Datum: 19.11.99
Name:.......................................
Hilfsmittel: Tafelwerk; MTC, Zeichengeräte, Millimeterpapier
HINWEIS: Der Lösungsweg muss deutlich erkennbar sein. Dazu gehören auch
Begründungen für Lösungsschritte, die nicht selbstverständlich sind.
1. Gegeben ist die Funktionenschar fa durch y = fa(x)= - x ln(a x2); a  R, a > 0, x 
D(fa).
1.1.
Geben Sie den größtmöglichen Definitionsbereich der Funktion fa an.
Zeigen Sie, dass die Funktion fa ungerade sind und bestimmen Sie die Nullstellen
sowie die Koordinaten der lokalen Extrempunkte. Weisen Sie die Art der Extrema
nach.
Ermitteln Sie eine Gleichung der Funktion g, auf deren Graphen alle lokalen
Extrempunkte der Funktion fa liegen.
Zeichnen Sie den Graphen der Funktionen f 0,1 , f0,2 und g in ein und dasselbe
Koordinatensystem.
Zeigen Sie, dass die Graphen der Funktionen f a keine gemeinsamen Punkte
besitzen.
2x
1.2. Weiterhin sind die Funktionen ht durch y = h r ( x ) = 2 2 mit t R, t0 , xR
x +t
gegeben.
Durch die Graphen der Funktionen h0,1 , h2 und die Geraden mit den
Gleichungen x = 1 und x = 2 wird eine Fläche vollständig begrenzt.
Ermitteln Sie mit dem MTC die Maßzahl dieser Fläche.
Für jede Funktion ht wird für jedes x ( x  R, x>0) durch die Punkte O( 0 / 0 ),
Q( x / 0 ) und P( x / ht(x) ) genau ein rechtwinkliges Dreieck bestimmt. Jedes
dieser Dreiecke erzeugt bei Rotation um die x-Achse einen geraden Kreiskegel.
Berechnen Sie die Stelle xt in Abhängigkeit von t, für die das Volumen des
zugehörigen Kreiskegels maximal ist.
Auf die Überprüfung einer hinreichenden Bedingung für die Existenz des lokalen
Maximums kann verzichtet werden.
2. Auf dem beigefügten Arbeitsblatt ist ein Quader dargestellt.
2.1. Bestimmen Sie die Koordinaten der Eckpunkte.
2.2.In den Quader wird ein Sechseck eingezeichnet.
Konstruktionsanweisung:
M1 sei der Mittelpunkt der Strecke AB.
M2 sei der Mittelpunkt der Strecke BC.
M3 sei der Mittelpunkt der Strecke CF.
M4 sei der Mittelpunkt der Strecke FG.
M5 sei der Mittelpunkt der Strecke GD.
M6 sei der Mittelpunkt der Strecke AD.
Ermitteln Sie die Koordinaten der einzelnen Streckenmitelpunkte.
Zeichen Sie das Sechseck in das Arbeitsblatt ein!
2.3. Die Gerade g verläuft durch die Punkte M1 und M4. Die Gerade h geht durch die
Punkte C und M6. Untersuchen Sie die gegenseitig Lage der Geraden g und h!
2.4. In diesem Koordinatensystem ist auch das Geradenbüschel k und die Gerade l
zu finden.
æ 1 ö æ 2k - 2 ö
æ 1 ö æ 1ö
ç ÷ ç
÷
ç ÷ ç ÷
k : x = ç - 1÷ + t ç 2 ÷ , k, t  R
l : x = ç 1 ÷ + sç 2 ÷ s  R
ç1÷ ç 0 ÷
ç13 ÷ ç 0 ÷
è ø è
ø
è ø è ø
Die Gerade l schneidet genau eine Gerade des Büschels k.
Ermitteln Sie den Schnittpunkt der beiden Geraden!
3. In einem kartesischen Koordinatensystem sind die Punkte A(-8; 1; 0),
B( 2; 1; 0) und C(-6; 5; 0) gegeben. Die Punkte A, B, C sind Eckpunkte eines
Dreiecks.
3.1.
Klassifizieren Sie dieses Dreieck hinsichtlich seiner Eigenschaften.
3.2.
Berechnen Sie die Koordinaten des Schnittpunktes der Mittelsenkrechten
dieses Dreiecks.
3.3.
Auf der positiven x3-Achse liegt der Punkt D, so daß gilt: Der Flächeninhalt des
Dreiecks ABD hat die Maßzahl 252 .
Berechnen Sie die Koordinaten von D.
( Ergebnis zur Kontrolle: D( 0; 0; 7) )
Berechnen Sie die Maßzahl des Volumens der Pyramide ABCD.
4. Beweisen Sie: Die Summe der von den Eckpunkten eines Dreiecks ABC zu
Mittelpunkten Ma, Mb und Mc der gegenüberliegenden Seiten führenden Vektoren
s a , s b bzw. s c ist der Nullvektor 0.
Arbeitsblatt : Kantenlänge des Quaders 6 LE
G
F
D
E
O
A
C
B
Arbeitsblatt : Kantenlänge des Quaders 6 LE
G
F
D
E
O
A
C
B