Übungsaufgaben

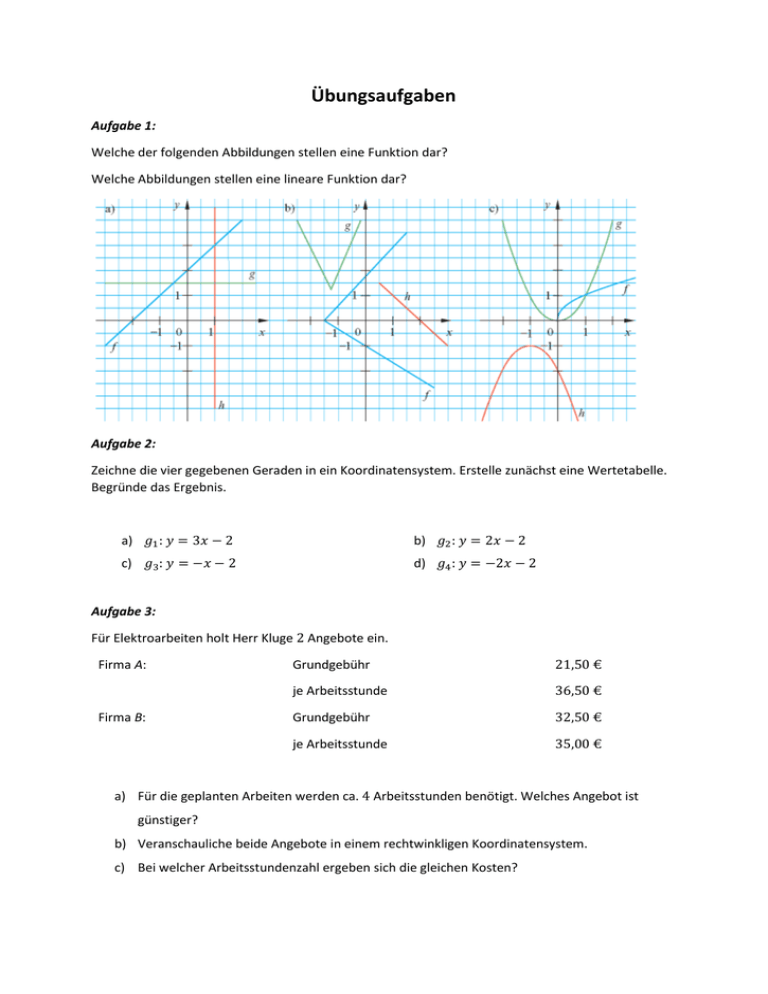
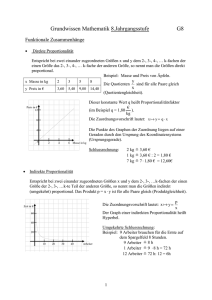
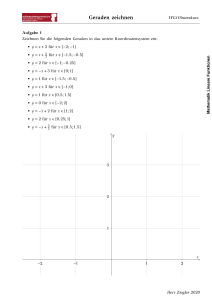
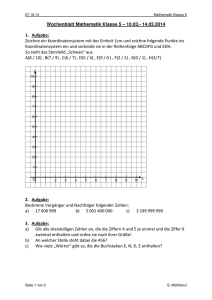
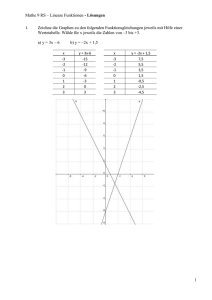
Übungsaufgaben
Aufgabe 1:
Welche der folgenden Abbildungen stellen eine Funktion dar?
Welche Abbildungen stellen eine lineare Funktion dar?
Aufgabe 2:
Zeichne die vier gegebenen Geraden in ein Koordinatensystem. Erstelle zunächst eine Wertetabelle.
Begründe das Ergebnis.
a) 𝑔1 : 𝑦 = 3𝑥 − 2
b) 𝑔2 : 𝑦 = 2𝑥 − 2
c) 𝑔3 : 𝑦 = −𝑥 − 2
d) 𝑔4 : 𝑦 = −2𝑥 − 2
Aufgabe 3:
Für Elektroarbeiten holt Herr Kluge 2 Angebote ein.
Firma A:
Firma B:
Grundgebühr
21,50 €
je Arbeitsstunde
36,50 €
Grundgebühr
32,50 €
je Arbeitsstunde
35,00 €
a) Für die geplanten Arbeiten werden ca. 4 Arbeitsstunden benötigt. Welches Angebot ist
günstiger?
b) Veranschauliche beide Angebote in einem rechtwinkligen Koordinatensystem.
c) Bei welcher Arbeitsstundenzahl ergeben sich die gleichen Kosten?
Aufgabe 4:
Setze nacheinander die Werte 0, 1, 2, 3, 4, 5 für 𝑥 in die Funktionsgleichungen ein und ermittle die 𝑦Werte. Trage diese in eine Wertetabelle ein. Zeichne den Graphen in ein Koordinatensystem. Achte
auf einen entsprechenden Maßstab.
Vergleiche den Verlauf der Graphen. Erkläre.
a) 𝑦 = 𝑥 + 3 und 𝑦 = 𝑥 − 3
b) 𝑦 = 2𝑥 + 4 und 𝑦 = 2𝑥 − 4
c) 𝑦 = 1,5𝑥 + 2 und 𝑦 = 1,5𝑥 − 2
1
2
3
4
1
2
d) 𝑦 = 𝑥 + und 𝑦 = 𝑥 −
3
4
Aufgabe 5:
Gegeben sind die Schnittpunkte der Graphen mit der 𝑦-Achse. Gib zu jedem Punkt zwei mögliche
Funktionsgleichungen linearer Funktionen an.
a) 𝑃 (0|4)
b) 𝑄 (0| − 2)
Stelle die gefundenen Geraden grafisch dar.
c) 𝑅 (0|3,5)
Lösung 1:
a)
f: lineare Funktion, 𝑦 = 𝑥 + 2 (−3 ≤ 𝑥 ≤ 2)
g: konstante Funktion (keine lineare Funktion)
h: keine Funktion
c)
f, g und h sind Funktionen, aber keine linearen
Funktionen.
b)
f: keine Funktion
g: Funktion, aber keine lineare Funktion
h: lineare Funktion, 𝑦 = −𝑥 + 2 (0,5 ≤ 𝑥 ≤ 3)
Lösung 2:
𝑥
−2
−1
0
1
2
1.
𝑦
−8
−5
−2
1
4
2.
𝑦
−6
−4
−2
0
2
3.
𝑦
0
−1
−2
−3
−4
4.
𝑦
2
0
−2
−4
−6
Da der Achsenabschnitt jeweils −2 ist, schneiden alle Geraden die
𝑦-Achse im Punkt (0| − 2).
Lösung 3:
a)
Das Angebot der Firma A ist günstiger.
Firma A:
21,50€ + 4 · 36,50€ = 167,50€
Firma B:
32,50€ + 4 · 35,00€ = 172,50€
b)
siehe Bild
c)
Bei einer Arbeitszeit von 7 h 20 min ergeben sich die gleichen Kosten
(289,17 €).
Lösung 4:
a)
𝑥
0
1
2
3
4
5
𝑦 =𝑥+3
3
4
5
6
7
8
𝑦 =𝑥−3
−3
−2
−1
0
1
2
Lösung 5:
a)
z. B. 𝑦 = 𝑥 + 4; 𝑦 = −2𝑥 + 4
b)
z. B. 𝑦 = 𝑥 − 2; 𝑦 = −3𝑥 − 2
c)
z. B. 𝑦 = 𝑥 + 3,5; 𝑦 = −𝑥 + 3,5