Hashing – Was bisher geschah: Hashfunktion h: U → {0,..., M − 1

Hashing – Was bisher geschah:
Hashfunktion h : U → {0, . . . , M − 1}, |U | ≫ M.
(Anforderungen: „streut gut“, (sehr) effizient berechenbar).
Will Schlüssel x ∈ U an Position h(x) speichern.
Geschlossenes Hashing:
• Kollisionen: Schlüssel x 6= x ′ mit h(x) = h(x ′ ).
Kommen vor (→ Geburtstagsparadoxon).
• Strategien für Kollisionsbehandlung:
– lineares Sondieren;
– multiplikatives Sondieren;
– quadratisches Sondieren; – doppelte Hashing.
• SEARCH, INSERT damit klar (evtl. Overflow bei INSERT).
• DELETE: Unterscheide Einträge „besetzt“,
„noch nie besetzt“, „wieder frei“.
Analyse geschlossenes Hashing:
Rechenzeiten für SEARCH, INSERT, DELETE?
Mit Analyse der Suche alles erledigt, zwei Fälle:
„Erfolgreiche Suche“, „Erfolglose Suche“.
• Worstcase ist schlecht: Zeit 2(n).
• Interessanter & typischerweise viel besser:
Durchschnittliche Zeit über zufällige Wahl der Schlüssel.
Analyse der vier Kollisionsstrategien ist schwierig.
Lineares Sondieren:
Betrachte 95% Auslastung bei großen Arrays.
• Erfolgreiche Suche:
durchschnittlich ungefähr 10, 5 Positionen.
• Erfolglose Suche:
durchschnittlich ungefähr 200, 5 Positionen.
Wir analysieren zum Vergleich ideales Hashing.
Modell des idealen Hashing:
M
Alle n Möglichkeiten, die n besetzten Plätze bei n Daten
auszuwählen, haben dieselbe Wahrscheinlichkeit.
Erfolgreiche Suche beim idealen Hashing
• Wieder n Daten bereits eingefügt.
• Gesuchtes Datum x sei als k-tes Datum eingefügt
worden, k ∈ {1, . . . , n}.
Erfolgreiche Suche nach x verläuft bis zum Finden von x
identisch zu der erfolglosen Suche nach x direkt vor dem
Einfügen von x.
Dann k − 1 besetzte Stellen, erwartete Suchzeit
Wenn nun jedes der n Daten mit Wskt.
1
n
M+1
M+1−(k−1) .
gesucht wird, be-
trägt die erwartete Suchzeit. . .
. – Seite 257/726
1 X
n
1≤k≤n
M +1
M +1
1
1
=
+ ··· +
.
M −k+2
n
M −n+2
M +1
|
{z
}
X 1
X
1
−
i
i
1≤i≤M+1
1+
1
2
+ ··· +
1
m
1≤i≤M−n+1
kommt oft vor, heißt harmonische Reihe,
ihr Wert wird mit H (m) bezeichnet.
Aber wie groß ist H (m) ungefähr?
. – Seite 258/726
ln(m + 1) ≤ H (m) ≤ ln m + 1, also H (m) ≈ ln m.
1
f (x) = 1x
H (m) =
1
2
1
3
1
4
m
X
i=1
1
2
3
4
1
≤1+
i
Zm
1
d x = ln m + 1
x
1
m
f (x) = 1x
1
H (m) =
1
2
1
3
1
4
m
X
1
i=1
1
2
3
4
i
≥
m+1
Z
1
d x = ln(m + 1)
x
1
m+1
. – Seite 259/726
Die erwartete Zeit einer erfolgreichen Suche beim
idealen Hashing beträgt
M +1
H (M + 1) − H (M − n + 1)
n
M +1
M +1
M +1
≈
ln(M +1)−ln(M −n +1) =
ln
.
n
n
M +1−n
Für n ≈ 0, 95 · (M + 1) ist dies
1
0,95
1
· ln 0,05
≈ 3, 15.
Ersparnisfaktor größer als 3 gegenüber linearem Sondieren.
. – Seite 260/726
Eine Variante des geschlossenen Hashing
An jeder Arrayposition Platz für c Daten.
Kollisionsbehandlung erst für c + 1 Daten an einem Platz.
Computed-Table bei OBDD-Synthese: c = 4 und keine
Kollisionsbehandlung, sondern Überschreiben der am
längsten nicht gelesenen Information.
. – Seite 261/726
Offenes Hashing
Vorteil: Auch DELETE wird unterstützt, kein Overflow.
Nachteil: mehr Speicherplatz durch Benutzung von Listen.
Datum x steht stets in der Liste L(h(x)).
SEARCH(x):
Berechne h(x) und
suche x in der Liste L(h(x)).
Zeit: ???
INSERT(x) nach erfolgloser Suche:
Füge x in L(h(x)) ein, z. B. stets vorne.
Zeit ohne Suche: O(1).
DELETE(x) nach erfolgreicher Suche:
Entferne x; nur effizient, wenn Zeiger auf x
bei der Suche gespeichert wird. Zeit ohne Suche: O(1).
. – Seite 262/726
Analyse der Suche bei offenem Hashing:
Zeit für Suche abhängig von Länge der Liste L(h(x)).
Aber wie lang wird die?
Zufällige Daten und „ideal streuende“ Hashfunktion.
Meint: Hashwerte gleichverteilt über {0, . . . , M − 1}.
Genauer: Definiere Zufallsvariablen
(
1, i-tes Datum kommt in j-te Liste;
X i j :=
0, sonst.
1
Dann: Prob(X i j = 1) = .
M
1
M −1
1
Also: E(X i j ) = 1 ·
+0·
= .
M
M
M
X j := X 1 j + · · · + X n j , zählt Daten in j-ter Liste.
E(X j ) = E(X 1 j
n
+ · · · + X n j ) = E(X 1 j ) + · · · + E(X n j ) = .
M
. – Seite 263/726
Erfolglose Suche in Liste j:
Inklusive nil-Zeiger durchschnittlich
n
Objekte betrachten.
1+ M
Falls n ≈ 0, 95 · M, ist dies ≈ 1, 95.
Erfolgreiche Suche in Liste j der Länge l:
Jede Position in der Liste hat Wskt. 1/l, also
1
l +1
(1 + 2 + · · · + l) =
.
l
2
Durchschnittliche Listenlänge hier: 1 + n−1
M ,
Liste enthält sicher das gesuchte Datum und die
anderen n − 1 Daten sind zufällig verteilt.
n−1
Also erwartete Suchdauer 12 (1 + n−1
+
1)
=
1
+
M
2M .
Falls n ≈ 0, 95 · M, ist dies ≈ 1, 475.
. – Seite 264/726
Offenes Hashing erlaubt n > M.
Falls n ≫ M, Rehashing wegen fallender Effizienz ratsam.
Universelles Hashing:
Alle Ergebnisse hier für zufällige Daten.
Problem: Absicherung gegen Worstcase?
Idee: Nicht Daten, sondern Hashfunktionen zufällig.
Wähle h zufällig aus Menge H von Hashfunktionen. Will:
• Alle Funktionen effizient auswertbar.
• Menge H nicht zu groß → kompakte Beschreibung
der Hashfunktionen.
• Gleiche Eigenschaften bez. Kollisionen wie bei
zufälligen Daten.
Das geht! Gutes erwartetes Verhalten bei allen Daten.
(→ Spezialvorlesung)
. – Seite 265/726
3.3 Binäre Suchbäume
In Kap. 3.3 – 3.7 Universum U vollständig geordnet.
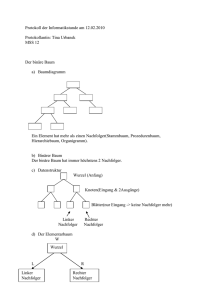
Definition: Binärer Suchbaum.
• Gewurzelter Baum mit Zeigern in Richtung Blätter.
• Innere Knoten dürfen nil-Zeiger und
Zeiger auf Knoten haben,
• Knoten enthalten ein Datum,
• Suchbaumeigenschaft: Knoten mit Datum x ⇒
– alle Daten im linken Teilbaum sind kleiner als x und
– alle Daten im rechten Teilbaum sind größer als x.
. – Seite 266/726
Espe
Kiefer
Erle
nil
Birke
Ahorn
nil
nil
Eiche
nil
Buche
nil
Fichte
nil
Tanne
Linde
nil
nil
nil
Ulme
nil
nil
nil
. – Seite 267/726
SEARCH(x):
– Starte an der Wurzel.
– Es wird Knoten mit Datum y erreicht.
– y = x, Suche erfolgreich.
– y > x, gehe zum linken Kind,
– y < x, gehe zum rechten Kind.
– Es wird ein nil-Zeiger erreicht.
– x ist nicht im Suchbaum enthalten.
INSERT(x) nach erfolgloser Suche:
– Der erreichte nil-Zeiger wird ersetzt durch einen Zeiger
auf
x
nil nil .
Zeit ohne Suche: O(1).
. – Seite 268/726
DELETE etwas später.
Die Suchzeit hängt von der Länge des Weges
Wurzel
Knoten mit Datum x bzw.
nil-Zeiger, wo x hingehört
ab.
Entstehen typischerweise gut balancierte Bäume?
Beispiel:
Füge eins, zwei, ..., zehn in einen leeren binären
Suchbaum ein. Im Bild keine nil-Zeiger.
. – Seite 269/726
eins
eins
eins
zwei
eins
drei
drei
eins
zwei
drei
vier
zwei
eins
zwei
drei
vier
zwei
vier
fünf
fünf
sechs
eins
eins
drei
drei
zwei
vier
acht
vier
zwei
fünf
fünf
sechs
sechs
sieben
sieben
eins
eins
drei
acht
drei
zwei
acht
vier
vier
zehn
fünf
fünf
sechs
sechs
neun
zwei
sieben
neun
sieben
. – Seite 270/726
Bilanz:
Nach Einfügen von „sieben“ schon ein Weg mit 6 Daten,
der dann aber nicht mehr verlängert wurde.
DELETE(x) nach erfolgreicher Suche, die den Zeiger auf
den Knoten v mit Datum x bereitstellt:
1. Fall: v ist Blatt.
Zeiger wird durch nil-Zeiger ersetzt.
(Knoten v wird freigegeben.)
2.Fall: v hat genau ein Kind.
Zeiger wird durch Zeiger auf Kind ersetzt.
(Knoten v wird freigegeben.)
. – Seite 271/726
3.Fall: v hat zwei Kinder.
Sei Tℓ Teilbaum unterhalb und inklusive linkem Kind.
• Suche in Tℓ größtes Datum y, das kleiner als x ist:
Gehe zum linken Kind von v und dann stets nach rechts
bis zu einem nil-Zeiger. Letztes Datum ist y.
• Vertausche x und y (kein Suchbaum mehr!).
• Entferne x im neuen Knoten (das ist Fall 1 oder Fall 2).
Korrektheit? Erst einmal Beispiele.
. – Seite 272/726
eins
drei
eins
zwei
drei
zwei
DELETE(sieben)
acht
vier
fünf
DELETE(zwei)
vier
acht
zehn
fünf
sechs
sechs
sieben
neun
zehn
neun
eins
eins
DELETE(vier)
vier
drei
acht
fünf
drei
zehn
sechs
acht
sechs
fünf
zehn
neun
neun
. – Seite 273/726
Korrektheit DELETE:
1. Fall: v hat gar kein Kind.
u
u
Korrektheit offensichtlich.
v
x
nil
nil nil
2. Fall: v hat genau ein Kind.
u
u
z
z
Vor DELETE Daten in v-Teilbaum alle < z
v
⇒ insbesondere für Teilbaum T .
x
Damit neuer Baum wieder Suchbaum.
nil
T
T
Analog für v mit linkem Kind.
. – Seite 274/726
Korrektheit DELETE (Forts.):
3. Fall: v hat zwei Kinder.
v
x
Gemäß Definition von y:
Tℓ
Tr
• y größtes Datum in Tℓ ⇒
Tℓ − {y} < y.
y
(Für alle Daten z in Tℓ außer y
nil
gilt z < y.)
v
Tℓ′
• y<x ⇒
y < Tr .
y
Tr
Damit neuer Baum nach Löschen von x
wieder Suchbaum.
x
nil
. – Seite 275/726
Analyse der erfolgreichen Suche
Annahme: Jedes der n Daten wird mit Wskt. 1/n gesucht.
Worstcase: „Lineare Liste“
durchschnittliche Suchzeit
1
n+1
· (1 + 2 + · · · + n) =
.
n
2
. – Seite 276/726