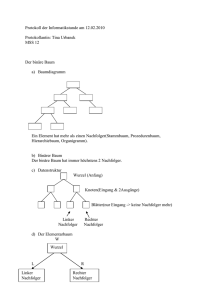
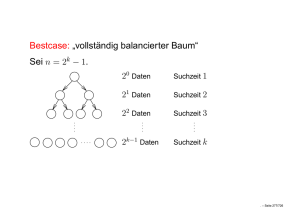
Graphen und Bäume
Werbung

Graphen und Bäume Graph Ein Graph besteht aus einer Menge von Knoten und Kanten. Die Knoten tragen Namen und sind durch die Kanten verbunden. Kann jede Kante eines Graphen in genau einer Richtung durchlaufen werden, so ist der Graph gerichtet. Ist jeder Kante eines Graphen ein Wert zugewiesen, so ist der Graph gewichtet. 2 Graph - Beispiele Aachen → Dortmund Dortmund → Aachen Client 2 → Client 1 Client 1 → Client 2 Strecke? Weg km Nein - - Ja Dortmund → Bochum → Aachen 210 Verbindung? Weg Bit/s Nein - - Ja Client 1→ Router 1 → Client 2 bei 20 Bits 3 s 3 Bäume Ein Baum ist ein spezieller Graph. Grundeigenschaften es gibt einen Knoten ohne Vater: die Wurzel jeder andere Knoten hat genau einen Vater Wurzel Beziehungen Innerer Knoten 62 6 ist Vater von 2 2 ist Sohn von 6 Blatt Weitere Eigenschaften Leere Elemente • keine Zyklen • von Wurzel zu einem Knoten genau ein Pfad 4 Bäume Pfad Unterbaum Pfad: alle Knoten von einem Knoten k1 zu einem Knoten k2 (z. B. 6 2 8) Pfadlänge: Anzahl der Knoten von einem Knoten k1 zu einem Knoten k2 Tiefe des Baumes: das Maximum aller Pfadlängen von der Wurzel zu einem Blatt Tiefe eines Knotens: Pfadlänge von der Wurzel zu diesem Knoten Unterbaum: beliebiger Knoten k mit allen Nachfolgern, k als Wurzel 5 Bäume Rekursive Definition Ein Baum ist leer oder er besteht aus einer Wurzel W und einer leeren oder nichtleeren Liste B1, B2, ..., Bn von Bäumen. Von W zur Wurzel Wi von Bi führt jeweils eine Kante. W W1 B1 ... ... ... W2 B2 ... ... 6 Bäume - Beispiele 7 Binärbäume Ein Binärbaum ist ein spezieller Baum. Rekursive Definition Ein Binärbaum ist leer oder er besteht aus einer Wurzel W und zwei Binärbäumen, dem linken und dem rechten Teilbaum. W W1 W2 B1 ... B2 ... ... ... 8 Binärbäume - Beispiele (1) 9 Binärbäume - Beispiele (2) 10 Binäre Suchbäume Ein Binärer Suchbaum ist ein spezieller Binärbaum Rekursive Definition Ein binärer Suchbaum ist leer oder besteht aus einer Wurzel und zwei binären Suchbäumen, dem linken und dem rechten Teilbaum. Der Inhalt des Wurzelknotens ist größer als alle Elemente im linken Suchbaum und kleiner als alle Elemente im rechten Suchbaum. • alle Knotenwerte von B1 sind echt kleiner als W • alle Knotenwerte von B2 sind echt größer als W • ... 11 Binäre Suchbäume - Beispiel Linker Teilbaum von 25: 3 < 25 10 < 25 11 < 25 Rechter Teilbaum von 25: 30 > 25 49 > 25 64 > 25 Linker Teilbaum von 10: 3 < 10 Rechter Teilbaum von 10 11 >10 ... 12 Binäre Suchbäume - Traversierung Preorder Durchlauf: Wurzel – Linker Knoten – Rechter Knoten (WLR) 25 10 3 11 49 30 64 13 Binäre Suchbäume - Traversierung Inorder Durchlauf: Linker Knoten – Wurzel – Rechter Knoten (LWR) 3 10 11 25 30 49 64 Sortiereigenschaft: Nach einem Inorder-Durchlauf ist die Zahlenfolge aufsteigend sortiert! 14 Binäre Suchbäume - Traversierung Postorder Durchlauf: Linker Knoten – Rechter Knoten – Wurzel (LRW) 3 11 10 30 64 49 25 15 Binäre Suchbäume - Traversierung Levelorder Durchlauf: Ebenenweise Zuerst Wurzel, dann Söhne der Wurzel, . . . 25 10 49 3 11 30 64 16 Binäre Suchbäume - Operationen Einfügen 25 Beispiel: 70 70 > 25 49 10 3 NIL 11 NIL NIL NIL NIL 70 > 64 64 30 NIL 70 > 49 NIL NIL NIL 70 NIL 17 Binäre Suchbäume - Operationen Löschen 25 1. Fall: Ein Blatt 49 10 3 NIL 11 NIL NIL NIL 64 30 NIL NIL Beispiel: 3 70 NIL NIL NIL 18 Binäre Suchbäume - Operationen Löschen 25 2. Fall: Ein innerer Knoten mit 1 Nachfolger 49 10 NIL 11 NIL NIL 64 30 NIL NIL Beispiel: 10 70 NIL NIL NIL 19 Binäre Suchbäume - Operationen Löschen 25 3. Fall: Einen inneren Knoten mit 2 Nachfolgern 49 11 NIL 30 NIL Vorgehen: Suche Knoten mit kleinstem Element im rechten Teilbaum und ersetze damit zu löschenden Knoten 64 Beispiel: 49 NIL NIL 70 NIL NIL 20