PDF

http://www.mpi-sb.mpg.de/~sschmitt/info5-ss01
IS
UN
R
S
SS 2001
E R SIT
S
Schmitt, Schömer
SA
IV
A
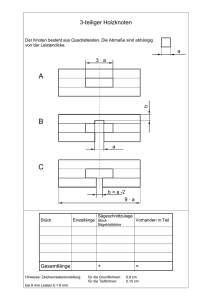
Grundlagen zu
Datenstrukturen und Algorithmen
A VIE N
Lösungsvorschläge für das 11. Übungsblatt
Letzte Änderung am 29. Juni 2001
Aufgabe 1 Definitionen aus der Vorlesung:
A0 (n) = 2n
(n)
Ak (n) = Ak−1 (1) k ≥ 1
I0 (n) = dn/2e
(i)
Ik (n) = min{i ∈ N | Ik−1 (n) = 1} k ≥ 1
α(n, n0 ) = min{k ∈ N0 | Ik (n) ≤ 2 + n0 }
a) Wir wählen z = AN (3 + n0 ). Es ist IN (AN (3 + n0 )) = 3 + n0 > 2 + n0 . Weiter folgt
Ik (AN (3 + n0 )) ≥ IN (AN (3 + n0 )) für alle 0 ≤ k < N wegen Lemma 8.7 aus dem Skript
(Ik+1 (n) ≤ Ik (n)). Damit gilt α(z, n0 ) > N .
b) Induktion nach k.
k = 0: ist klar.
k → k + 1: Nach Induktionsvoraussetzung ist Ik (n) monoton wachsend. Für m ≥ n gilt also:
Ik (m) ≥ Ik (n). Man kann sich jetzt wirklich leicht überlegen (Induktion nach i), daß damit
(i)
(i)
auch für alle i ∈ N gilt Ik (m) ≥ Ik (n). Damit folgt direkt Ik+1 (m) ≥ Ik+1 (n).
Die Funktionen sind nicht alle streng monoton wachsend, wie man an I0 sehen kann.
b) Sei N ∈ N beliebig. Dann existiert ein z ∈ N0 mit α(z, n0 ) > N , insbesondere Ik (z) > 2 + n0
für alle 0 ≤ k ≤ N . Da die Ik monoton wachsend sind, folgt
Ik (n) ≥ Ik (z) > 2 + n0
für alle n ∈ N0 , n ≥ z und für alle 0 ≤ k ≤ N . Für diese n ist dann auch α(n, n0 ) > N .
Wir haben gezeigt: Für alle N ∈ N existiert ein z ∈ N0 , so daß für alle n ≥ z gilt α(n, n0 ) >
N . Damit folgt die Behauptung.
Aufgabe 2
a) h = 0: Ein Knoten der Höhe 0 ist ein Blatt, der Unterbaum besteht also aus 1 = 20 Knoten.
h → h + 1: u hat die Höhe h + 1. Damit besitzt u also mindestens einen Kinderknoten v,
dessen Höhe h ist. Nach Induktionsvoraussetzung hat der Unterbaum mit Wurzel v dann
mindestens 2h Knoten.
v wurde irgendwann mit einem union als Kind von u eingefügt. Zu diesem Zeitpunkt hatte
der Unterbaum mit Wurzel u mindestens so viele Knoten wie der Unterbaum mit Wurzel
v, also auch mindestens 2h . Da keine Knoten gelöscht werden, sondern höchstens welche
dazugefügt werden, hat der Unterbaum mit Wurzel u also mindestens 2·2h = 2h+1 Elemente.
b) Jeder Knoten u der Höhe h steht also für einen Unterbaum mit mindestens 2h Elementen.
Sei k die Anzahl der Knoten mit Höhe h. In diesen k Unterbäumen sind dann mindestens
k · 2h Knoten. Insgesamt haben wir n Knoten im Baum, so daß damit k ≤ 2nh folgt. Es kann
also nur 2nh Knoten der Höhe h im Baum geben.
c) Im Skript wurde gezeigt, daß die Höhe jedes Knotens ≤ log n ist. Es folgt
log n
X
h(u) ≤
Knoten
X
h·
h=0
u
n−1
X
n
h
≤
n
,
h
2h
2
h=0
wenn n groß genug ist (so daß log n ≤ n − 1 ist). Mit dem ersten Übungsblatt folgt
n−1
X
h
=
h
2
h=0
Man kann zeigen, daß
1 n
2
1
n − n − 21
2
2
1
−
1
2
+
1
2
n
1
=2
(−n − 1) + 1 .
2
n
1
(−n − 1) + 1 = 2
lim 2
n→∞
2
ist (Anwendung von L’Hospital). Damit folgt
∞
X
h
=2
2h
h=0
und
X
Knoten
h(u) ≤ n
∞
X
h
= 2n.
2h
h=0
u
d) Satz: Führt man auf einer Partition einer Menge mit n Elementen n−1 union-Operationen
und m find-Operationen durch, so hat man bei Verwendung von Bäumen mit Pfadkomprimierung eine Laufzeit von O((n + m)α(n, 1)).
Beweis: Im Skript wurde gezeigt:

Gesamtzahl aller Umhängungen = O 
X
Knoten

u

h(u) + 3n + m α(n, 1) .
Dies ist auch gerade die Gesamtlänge der Pfade P1 , . . . , Pm , entlang derer die Komprimierung stattfindet.
P
Die Behauptung folgt dann direkt mit Knoten u h(u) = O(n).
Aufgabe 3
void top_sort(graph G)
{
/* Initialisierung */
/* Laufzeit: O(|V|+|E|) */
for(i=0; i<n; i++) indeg[i]=0; //
for(i=0; i<n; i++)
//
{
//
forall ((i,j) in E) indeg[j]++;
}
n = |V|,
indeg[i] = Eingangsgrad des
Knotens i
// Durchlauf durch die
// Adjazenzliste von i
/* Alle Knoten mit Eingangsgrad 0 in queue rein */
/* Laufzeit: O(|V|) */
queue S;
for(i=0; i<n; i++)
{
if(indeg[i]==0) S.enqueue(i);
}
/* Laufzeit fuer while-Schleife: O(|V|+|E|) */
/* Jede Kante und jeder Knoten werden hoechstens einmal betrachtet */
k=0;
while(!S.empty())
{
i = S.dequeue(); // liefert das 1. Element und entfernt es aus S
ord[i] = k;
// gebe dem Knoten eine kleine Nummer
k++;
/* loesche die Kanten, die von i ausgehen */
/* nicht wirklich loeschen... */
forall((i,j) in E) // Adjazenzliste durchlaufen
{
indeg[j]--;
// j verliert eine Kante.
if(indeg[j]==0) S.enqueue(j);
}
}
assert(k==n); // sonst enthaelt der Graph einen Zyklus
}
Aufgabe 4
a), b) Betrachte jede Wabe als einen Knoten. Jede Kante zwischen zwei Knoten entspricht zwei
benachbarten Waben. Die Matrix A ist dann die Adjazenzliste dieses Graphen: Aij = 1,
falls Kante von Knoten i zu Knoten j existiert, = 0 sonst. Da der Graph ungerichtet ist, ist
die Matrix symmetrisch (d.h. AT = A).

0 1 0
 1 0 1

 0 1 0

 1 0 0

 1 1 0
A=
 0 1 1

 0 0 1

 0 0 0

 0 0 0
0 0 0
1
0
0
0
1
0
0
1
0
0
1
1
0
1
0
1
0
1
1
0
0
1
1
0
1
0
1
0
1
1
0
0
1
0
0
1
0
0
0
1
0
0
0
1
1
0
0
0
1
0
0
0
0
0
1
1
0
1
0
1
0
0
0
0
0
1
1
0
1
0
















Im Vektor x ist die (unbekannte) Verteilung des Honig kodiert. Dabei entspricht 1 einer
gefüllten Wabe, 0 einer leeren Wabe.
 
1
 0 
 
 0 
 
 0 
 
 1 

x=
 1 
 
 1 
 
 0 
 
 0 
0
Der Vektor b entspricht den angegebenen Zahlen:
 
1
 3 
 
 2 
 
 2 
 
 2 

b=
 2 .
 
 1 
 
 1 
 
 2 
2
Das kann man sich folgendermaßen überlegen. Um die Zahl in der i-ten Wabe zu erhalten,
muß man die benachbarten Waben betrachten (also genau die, für die in der Adjazenzliste
eine 1 steht). Für jede benachbarte Wabe addiert man 1, falls diese gefüllt ist, und 0 sonst.
Damit erhält man das Gleichungssystem.
c) Man kann sich das Gleichungssystem wie oben erzeugen (37 × 37 Matrix) und zeigen, daß
dieses System eindeutig lösbar ist, indem man die Determinante dieser Matrix bestimmt. Ist
diese 6= 0, so ist das System eindeutlig lösbar. Die Lösung kann man auch einfach berechnen.
Grafische Darstellung der Lösung:
1
2
1
3
4
1
3
3
2
1
2
2
2
1
4
1
2
2
4
2
3
3
3
2
2
4
5
2
1
3
2
4
4
3
1
2
1