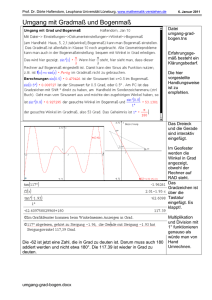
Geometrische Veranschaulichung des Rechnens in der Menge C

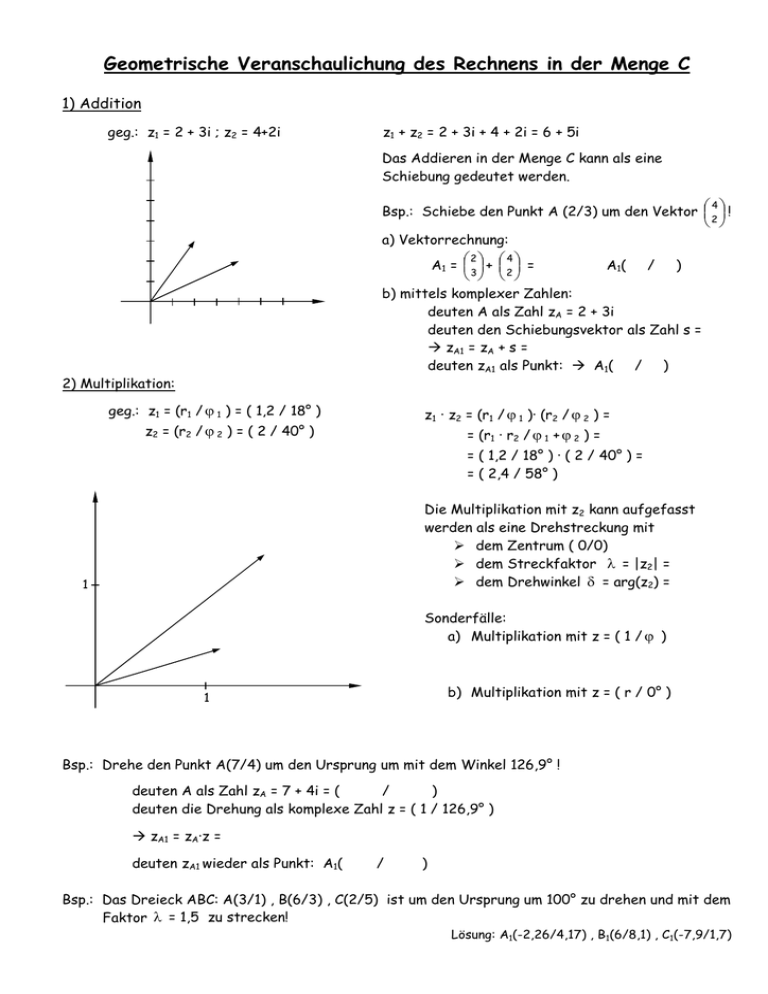
Geometrische Veranschaulichung des Rechnens in der Menge C
1) Addition
geg.: z1 = 2 + 3i ; z2 = 4+2i
z1 + z2 = 2 + 3i + 4 + 2i = 6 + 5i
Das Addieren in der Menge C kann als eine
Schiebung gedeutet werden.
4
Bsp.: Schiebe den Punkt A (2/3) um den Vektor  2  !
 
a) Vektorrechnung:
2
4
A1 =  3  +  2  =
   
A1(
/
)
b) mittels komplexer Zahlen:
deuten A als Zahl zA = 2 + 3i
deuten den Schiebungsvektor als Zahl s =
zA1 = zA + s =
deuten zA1 als Punkt: A1( / )
2) Multiplikation:
geg.: z1 = (r1 / ϕ 1 ) = ( 1,2 / 18° )
z1 · z2 = (r1 / ϕ 1 )· (r2 / ϕ 2 ) =
z2 = (r2 / ϕ 2 ) = ( 2 / 40° )
= (r1 · r2 / ϕ 1 + ϕ 2 ) =
= ( 1,2 / 18° ) · ( 2 / 40° ) =
= ( 2,4 / 58° )
Die Multiplikation mit z2 kann aufgefasst
werden als eine Drehstreckung mit
dem Zentrum ( 0/0)
dem Streckfaktor λ = |z2| =
dem Drehwinkel δ = arg(z2) =
1
Sonderfälle:
a) Multiplikation mit z = ( 1 / ϕ )
b) Multiplikation mit z = ( r / 0° )
1
Bsp.: Drehe den Punkt A(7/4) um den Ursprung um mit dem Winkel 126,9° !
deuten A als Zahl zA = 7 + 4i = (
/
)
deuten die Drehung als komplexe Zahl z = ( 1 / 126,9° )
zA1 = zA·z =
deuten zA1 wieder als Punkt: A1(
/
)
Bsp.: Das Dreieck ABC: A(3/1) , B(6/3) , C(2/5) ist um den Ursprung um 100° zu drehen und mit dem
Faktor λ = 1,5 zu strecken!
Lösung: A1(-2,26/4,17) , B1(6/8,1) , C1(-7,9/1,7)