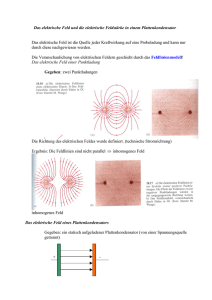
Kein Folientitel - Institut für Elektrische Energiewandlung
Werbung

Elektrische Maschinen und Antriebe Vorlesungsinhalt 1. Einleitung 2. Drehfelder in elektrischen Maschinen 3. Mathematische Analyse von Luftspaltfeldern 4. Spannungsinduktion in Drehstrommaschinen 5. Die Schleifringläufer-Asynchronmaschine 6. Die Kurzschlussläufer-Asynchronmaschine 7. Antriebstechnik mit der Asynchronmaschine 8. Die Synchronmaschine 9. Erregereinrichtungen und Kennlinien 10. Gleichstromantriebe TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/1 Institut für Elektrische Energiewandlung • FB 18 10. Gleichstromantriebe Quelle: Siemens AG TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/2 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe 10. Gleichstromantriebe 10.1 Die Funktionsweise der Gleichstrommaschine 10.2 Ankerwicklungen 10.3 Induzierte Spannung und elektromagnetisches Drehmoment 10.4 Ankerrückwirkung und Kompensationswicklung 10.5 Kommutierung des Ankerstroms und die Funktion der Wendepole & Dynamische Gleichungen von Gleichstrommaschinen 10.6 Generator- und Motorschaltungen der Gleichstrommaschine 10.7 Der drehzahlveränderbare Gleichstromantrieb 10.8 Leistungsgrenzen der Gleichstrommaschine TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/3 Institut für Elektrische Energiewandlung • FB 18 Einsatzgebiete von Gleichstrommaschinen mit Stromrichterspeisung Drehzahlveränderbare Antriebe z. B. mit geregelter Drehzahl: – in der Industrie z. B. in Walzwerken, Prüfständen, Kranen, für Drahtziehen, Stanzen, Kunststoffspritzguss, Folienrecken,... – in der Traktion als U-Bahn-, Straßenbahn- und Vollbahnmotoren, in E-Autos, – in Schiffen als U-Boot-Antriebe, Drehzahlveränderbare Kleinmotoren: – als permanentmagneterregter Kleinmotor in Automobilen (Fensterheber, Sitzversteller,..), als Tachogeneratoren,... (DC-Betrieb) – als ele. erregter Universalmotor in vielen Haushaltsgeräten (AC-Betrieb). TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/4 Institut für Elektrische Energiewandlung • FB 18 Kleine permanentmagneterregte Gleichstrommaschinen Quelle: Faulhaber, Germany Gleichstrom-Kleinstmotoren für Präzisionsantriebe TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/5 Institut für Elektrische Energiewandlung • FB 18 Vierpolige Gleichstrommaschine – Querschnitt Quelle: H. Kleinrath, Studientext Elektrische Felderregung / Bsp.: Vierpolige Maschine TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/6 Institut für Elektrische Energiewandlung • FB 18 Gleichstrommaschine – Längsschnitt le Quelle: H. Kleinrath, Studientext Elektrische Felderregung / Bsp.: Vierpolige Maschine TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/7 Institut für Elektrische Energiewandlung • FB 18 Zweipoliges Erregerfeld der Gleichstrommaschine f N f , Pol I f Beispiel für geschlossene Kurve C elektrisch erregt mit Polspule If: Erregerstrom (Feldstrom) DC Nf,Pol: Windungszahl je Polspule Durchflutungssatz für geschlossene Kurve C: H ds 2 f H Fe,s sFe,s H Fe,r sFe,r 2H sFe,r C Für Fe >> 0 ist HFe 0: H f sFe,s • B 0 f / B ,m Zwei Hauptpole (2p = 2, p: Polpaarzahl) erregen Luftspaltfeld B(x), eine Ankerspule rotiert mit Drehzahl n, zwei Kohlebürsten als Anschlüsse TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/8 Institut für Elektrische Energiewandlung • FB 18 Luftspaltfeldverteilung unter den Hauptpolen f N f , Pol I f Polkantenfeld streut in die Pollücken = „glockenförmige“ B-Feldkurve Fluss pro Pol: p l B ( x) dx e B ,m p l 0 p: Polteilung bp: Polbreite e: ideelle Polbedeckung TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/9 Institut für Elektrische Energiewandlung • FB 18 Elektrische Statorfelderregung Feldlinie = Kurve C Durchflutungssatz (Kurve C): H ds 2 N f ,Pol I f Nf,Pol Windungen je Statorpolspule C Eisenpermeabilität sehr groß (ungesättigt): Fe 0 : H Fe H 2 H ( x ) ( x ) 2 N f , Pol I f H ,m Ständerfeld im Luftspalt, elektrisch erregt durch Gleichstrom If TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/10 N f , Pol I f B ,m 0 N f , Pol I f Institut für Elektrische Energiewandlung • FB 18 Magnetischer Statorfluss pro Pol Radialkomponente der Flussdichte im Luftspalt p Polfluss: le B ( x)dx e ple B ,m 0 TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/11 Institut für Elektrische Energiewandlung • FB 18 Gleichstrommaschine – Felderregungsarten Beispiel: Vierpolige Maschinen Quelle: ABB, Schweden Quelle: Siemens AG Elektrische Felderregung Permanentmagneterregung 1: Feldspulen, 2: Kompensationswicklung 1, 2: Ferrit-Feldmagnete, 3: Polschuhblech, 3: Wendepolwicklung, 4: Ankerwicklung 4: Gehäuse als Jochrückschluss 5: Anker (Rotor) TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/12 Institut für Elektrische Energiewandlung • FB 18 Gleichstrommaschine – Prinzipielle Funktionsweise e ee Rotierende Läuferspule im Ständerfeld mit mechanischem Gleichrichter (Kommutator) Ständerfeld im Luftspalt, elektrisch erregt – In jede der bewegten Spulenseiten (Windungszahl Nc, Länge le, Drehzahl n) wird durch Bewegungsinduktion eine Wechselspannung ui,c induziert: Amplitude TECHNISCHE UNIVERSITÄT DARMSTADT Uˆ i ,c 2va B ,m N cle Prof. A. Binder : Elektrische Maschinen und Antriebe 10/13 Institut für Elektrische Energiewandlung • FB 18 Bewegungsinduktion in eine Ankerspule e e v a B E b v a B va B TECHNISCHE UNIVERSITÄT DARMSTADT le le 0 0 U ic 2 E b d s 2 v a B d s 2 va B le v a B d s Prof. A. Binder : Elektrische Maschinen und Antriebe 10/14 Institut für Elektrische Energiewandlung • FB 18 Spannungsinduktion in bewegten Leiter Rotoreisen va Eb Fe >> 0: B-Feldlinien treten (nahezu) senkrecht aus dem Eisen in den Luftspalt = radiale Feldrichtung. Dadurch sind va und B senkrecht zueinander gerichtet Eb va B Eb va B ez Luftspalt B Statoreisen Die bewegungsinduzierte Feldstärke Eb ist in axiale Richtung (z-Achse) gerichtet! Induzierte Spannung je Spulenseite (Länge le): l e ui,c / 2 Eb ds va B ez ez ds va B le le 0 0 ui,c (ui,c / 2) (ui,c / 2) 2va B le TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/15 Institut für Elektrische Energiewandlung • FB 18 Induzierte Anker-Spulenspannung Gleichgerichtete Spulen-Spannung ui e m 2 n Nc 1 : Spulen-Wechselspannung uic e e Gleichgerichtete Spulen-Spannung ui TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/16 Institut für Elektrische Energiewandlung • FB 18 Kurvenform der induzierten Ankerspulenspannung Nc 1 : U i,c,av 2 va B ,av le e • Uˆ i,c 2 va B ,m le Unter den Polen ist B(x) groß mit Maximalwert B,m, daher auch ui groß. In den Pollücken wechselt das Feld die Polarität: Nulldurchgang von Feld und Spannung. • Amplitude der gleichgerichteten Spulenspannung: Uˆ i,c 2 va B ,m le , Mittelwert entspricht einer Spannungsinduktion im mittleren Feld (ohne Pollücken): ui,av 2 va B ,av le • Einbrüche der Spannung im Abstand T/2 “unschön” (fa = 1/T „Ankerfrequenz“). TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/17 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe Zusammenfassung: Die Funktionsweise der Gleichstrommaschine (1) - Magnetisches Gleichfeld im Stator induziert Wechselspannung im Rotor (Anker) - Mechanischer Gleichrichter (Kommutator und Kohlegraphit-Bürsten) erzeugen Gleichspannung - Elektrische oder permanentmagnetische Ständerfelderregung TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/18 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe Zusammenfassung: Die Funktionsweise der Gleichstrommaschine (2) - Ruhendes magnetisches Erregerfeld (Statorfeld) als Gleichfeld - Rotierender geblechter Eisenkörper (Anker) mit Ankerspule(n) - Bewegungsinduzierte Wechselspannung in der Ankerspule - Über Kommutator und Bürsten gleichgerichtete Ankerspannung - Ankerspannung proportional zur Drehzahl - Läufer = Rotor = „Anker“, weil bei zweinutigem Läufer als „Doppel-T-Anker“ Ähnlichkeit mit Schiffsanker Nut Ankerspule Doppel-T-Anker TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/19 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe 10. Gleichstromantriebe 10.1 Die Funktionsweise der Gleichstrommaschine 10.2 Ankerwicklungen 10.3 Induzierte Spannung und elektromagnetisches Drehmoment 10.4 Ankerrückwirkung und Kompensationswicklung 10.5 Kommutierung des Ankerstroms und die Funktion der Wendepole 10.6 Generator- und Motorschaltungen der Gleichstrommaschine 10.7 Der drehzahlveränderbare Gleichstromantrieb 10.8 Leistungsgrenzen der Gleichstrommaschine TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/20 Institut für Elektrische Energiewandlung • FB 18 Induzierte gleichgerichtete Ankerspulenspannung 1 Ankerspule Abgewickelte Darstellung Kommutatorsegment Bürste Ui als „innere“ Spannung U i ~ v B (Quellenspannung Uq) Elektrisches Ersatzschaltbild im Generatorbetrieb im ErzeugerZählpfeilsystem (EZS) ic = ia ui 0, ic 0 ui ic TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/21 Institut für Elektrische Energiewandlung • FB 18 Induktion in eine Leiterschleife - Ersatzschaltbild Ersatzschaltbild: i i R ui i R u ui u ui i ui d / dt u ui R i u R i d / dt u R i uq R: Schleifen-Widerstand u: Klemmenspannung ui: induzierte Spannung uq = -ui: Quellen-Spannung uq ui d / dt R uq Verbraucher-Zählpfeilsystem für u, i Beispiel: a) Leerlaufende Schleife: i = 0 u = -ui = uq = d/dt b) Kurzgeschlossene Schleife: u = 0 i = ui/R = -uq/R = -(d/dt)/R NEGATIVER Strom! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/22 u Institut für Elektrische Energiewandlung • FB 18 Die LORENTZ-Kraft auf einen Ankerleiter Generatorbetrieb: EZS ui 0, I c 0 ui I c c Die LORENTZ-Kraft F wirkt gegen die Ankerumfangsgeschwindigkeit v = va und bremst! Bremsen Ui als „innere“ Spannung (Quellenspannung Uq) Motorbetrieb: VZS ui 0, I c 0 ui I c c Die LORENTZ-Kraft F wirkt in Richtung der Ankerumfangsgeschwindigkeit v und treibt an! Antreiben • • c Strom Ic im Leiter im Magnetfeld B Kraftwirkung F (LORENTZ-Kraft) maximal, wenn zwischen B- und Stromflussrichtung rechter Winkel. l l F I c (ds B) F I c ds B I c B l 0 TECHNISCHE UNIVERSITÄT DARMSTADT Nc Windungen je Ankerspule: F N c I c B l 0 Prof. A. Binder : Elektrische Maschinen und Antriebe 10/23 Institut für Elektrische Energiewandlung • FB 18 Zweischichtwicklung im Anker Einschichtwicklung Zweischichtwicklung: doppelte Spulenzahl = 2ic ic = ia 1 Spule K = 2, 2p = 2, K: Kommutatorstegzahl TECHNISCHE UNIVERSITÄT DARMSTADT c c 2 Spulen Spulenzahl je Parallelzweig: K/(2p) = 1 Prof. A. Binder : Elektrische Maschinen und Antriebe 10/24 Institut für Elektrische Energiewandlung • FB 18 Spannungskurvenform der Ankerspannung Nc 1 : U i,c,av 2 va B ,av le Vereinfachter Kurvenverlauf: 2 2 U i,c,av e Uˆ i,c TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/25 Institut für Elektrische Energiewandlung • FB 18 Erhöhung der Spulenzahl im Anker Beispiel: K = 4, 2p = 2: Spulenzahl K = 4, Spulenzahl je Parallelzweig: K/(2p) = 2 „Vergleichmäßigung“ der gleichgerichteten induzierten Spannung Spule 1 Spule 2 Spule Spule T TECHNISCHE UNIVERSITÄT DARMSTADT 1 1 n p fa Prof. A. Binder : Elektrische Maschinen und Antriebe 10/26 TC 1 n K Institut für Elektrische Energiewandlung • FB 18 Erzeugung einer glatten induzierten Spannung durch Serienschaltung von Ankerspulen idealisiert Uˆ i ,c 2 N cva B ,mle U Uˆ i ,c,av e i ,c Beispiel: 2p = 2, K = 6 K/2 = 3 um je eine Nutteilung räumlich versetzte Spulen mit Windungszahl Nc realer Verlauf TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/27 Institut für Elektrische Energiewandlung • FB 18 Abgewickelte Darstellung der Ankerwicklung K/2 Zweischichtwicklung: 2 parallele Ankerwicklungszweige 2 Pole 2. Parallelzweig Unterschicht Oberschicht 1. Parallelzweig Abgewickelt: Draufsicht auf Hauptpole 1 2 3 4 5 6 7 8 9 N 10 11 12 Beispiel: Spulenzahl je Parallelzweig: K/2 = 6 K = 12 Ankerspulen bzw. Kommutatorlamellen S Q = 12 Ankernuten 10 11 12 1 B 2 Ia 3 4 5 6 7 A K/2 8 Ia 9 10 Kommutatorsegmente Jede Spule beginnt/endet an einem Kommutatorsegment: Segmentzahl K TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/28 Institut für Elektrische Energiewandlung • FB 18 Wicklungsschritte bei der Schleifenwicklung Beispiel: K = 12, u = 1, Qr = 12, Nc = 1, z = 2.u.Nc.Qr = 24 Oberschicht Unterschicht 7 le 6 5 y1 4 3 2 Spulenschritte: 1 Von 1 Unterschicht nach 7 Oberschicht: y1 K/(2p) = 7 - 1 = 6 y2 Von 7 Oberschicht nach 2 Unterschicht: y2 = 7 - 2 = 5 Kommutatorschritt: y = y1 – y2 = 6 – 5 = 1 y 10 9 8 7 6 3 (=6) TECHNISCHE UNIVERSITÄT DARMSTADT 2 1 12 11 10 Von Kommutatorsegment 1 nach Segment 2: y = 2 - 1 = 1 Prof. A. Binder : Elektrische Maschinen und Antriebe 10/29 Institut für Elektrische Energiewandlung • FB 18 “Glättung” der induzierten Ankerspannung • • • • Mehrere Spulen werden in Serie geschaltet und an gegeneinander isolierte Kommutatorsegmente (“Lamellen”, „Stege“) gelötet (“Schleifenwicklung”). In den Spulen wird die Spannung nacheinander induziert. Die Serienschaltung (Spannungssumme) “verschmiert” die Einbrüche der gleichgerichteten Spannung. Zwischen Plus- und Minusbürste (Gleitkontakt) liegen K/2 Spulen in Serie (z.B.: K/2 = 6). Weitere K/2 Spulen lassen sich durch Fortsetzung des Schemas endlos anfügen. Allgemein: K/(2p) Spulen zwischen benachbarten Bürsten ! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/30 Institut für Elektrische Energiewandlung • FB 18 Wie wirkt sich das Liegen der Leiter in den Eisennuten bezüglich der Spannungsinduktion aus? - Wegen der hohen Eisenpermeabilität fließt das Magnetfeld an den Nutenleitern vorbei durch die Zähne - B-Feld am Nutenleiter BQ ist daher viel kleiner als B im Luftspalt - Die bewegungsinduzierte Spannung uic,Q ~ Eb,Q ist daher viel kleiner als die mit dem Luftspaltfeld B ersatzweise berechnete induzierte Spannung uic ~ Eb - Wieso stimmt TROTZDEM diese Ersatz-Berechnung mit der Wirklichkeit überein? ANTWORT 1: Eb,Q v BQ Eb Eb va B Umgehen dieses Paradoxons durch direkte Berechnung von uic = -dc/dt ANTWORT 2: Auflösung des Paradoxons durch genaue Betrachtung der Nutfeldänderung TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/31 Institut für Elektrische Energiewandlung • FB 18 ANTWORT 1: Spannungsinduktion uic = -dc/dt Quelle: ABB, Schweden Änderung der Flussverkettung c jeder Läuferspule: Von der Ankerspule umfasster Fluss c(t) + W va Ankerspule n Stator-Luftspaltfeld ist B 0 GLEICH-Feld: t TECHNISCHE UNIVERSITÄT DARMSTADT d c d c d uic Nc N c B dA dt dt dt A B Nc dA N c (va B ) ds Eb ds t A C N C c Wir können also mit Eb so rechnen, als ob die Spulenleiter an der Läuferoberfläche und NICHT in den Nuten liegen! Prof. A. Binder : Elektrische Maschinen und Antriebe 10/32 Institut für Elektrische Energiewandlung • FB 18 ANTWORT 2: Betrachtung der Spulenfeldänderung Bc Aus der Sicht eines ruhenden Beobachters im Stator erfährt die bewegte Ankerspule a) eine Bewegungsinduktion in dem kleinen Nutenfeld Bc = BQ E v B E b,Q Q b b) Die Bewegung des Läufers mit seiner Nut-Zahn-Struktur ändert auf der Spulenfläche Ac im Bereich der von der Spule umfassten Nuten und Zähne lokal die SpulenFlussdichte Bc: Wenn sich am Ort x1 ein Zahn befindet, ist dort die Flussdichte hoch, und am Ort x2, wo eine Nut ist, ist die Flussdichte niedrig. Wenig später ist bei x1 eine Nut und bei x2 ein Zahn: Die Flussdichte Bc schwankt daher an den Orten x1, x2 mit der HOHEN Nutfrequenz n.Qr. Bc / t a) + b): Resultierende induzierte Spannung: Bc Bc d uic N c dA Eb,Q ds N c dA (v BQ ) ds N c dt Ac t Ac t C C d c d c d N c Bc dA N c uic gemäß ANTWORT 1 dt A dt dt Bc dA Ac c Wir können wieder mit Eb aus dem Luftspaltfeld rechnen, so als ob die Spulenleiter an der Läuferoberfläche und NICHT in den Nuten liegen! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/33 Institut für Elektrische Energiewandlung • FB 18 Aufbau der Ankerspulen und des Kommutators Anker-Blechpaket beim Bewickeln u=3 Kommutator Quelle: H. Kleinrath, Studientext Ankerspulen Quelle: Fa. Brenner, Bürstadt - Zweischichtwicklung: pro Nut (Ober-/Unterschicht) = doppelt so viele Spulen unterbringbar - Mehrere (= u) Spulenseiten nebeneinander in eine Nut = gröbere Nutung möglich (billiger) - Durch Ober- und Unterschicht-Anordnung entsteht ein zweiter Parallelzweig je Polpaar in der Ankerwicklung, in dem auch ui,av induziert wird. TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/34 Institut für Elektrische Energiewandlung • FB 18 Zweischicht-Anker-Schleifenwicklung (= 5) p Oberschicht Unterschicht le u=3 Ankernut Oberschicht Unterschicht (= 4) Einlegen einer Ankerspule in zwei Ankernuten Ankerspule als Grundelement y = y1 – y2 = 5 – 4 = 1 y1 = K/(2p) = Spulenschritt = etwa Polteilung p Verbindung zur nächsten Ankerspule am Kommutator y = y1 – y2 = 1: „Kommutatorschritt“ TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/35 Institut für Elektrische Energiewandlung • FB 18 Begriffe der Zweischicht-Ankerwicklung Beispiel: 2p = 2, K = 12 Spulen in 12 Nuten: K : Kommutatorstegzahl ( = 12) u : Spulenseiten je Nut und Schicht ( = 1) 1. Spule: 1 OS – 7 US 2. Spule: 2 OS – 8 US… ……………….. 12. Spule: 12 OS – 6 US 1. Spule: 1 OS – 7 US usw. in sich geschlossen Qr : Ankernutzahl ( = 12) K = u . Qr ( = 1.12 = 12) Nc : Ankerspulenwindungszahl (z. B.: 7) z : Ankerleiterzahl z = 2 . u . Nc . Qr ( = 2.1.7.12 = 168) 2p : Polzahl ( = 2) OS US Jede Spule beginnt/endet an einem Kommutatorsegment: Segmentzahl K u Qr TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/36 Institut für Elektrische Energiewandlung • FB 18 Ankerspulen in Läufernuten S-Pol Beispiel: 2p = 2, K = 12 Spulen in 12 Nuten: OBER-Schicht (OS) 1. Spule: 1 OS – 7 US 2. Spule: 2 OS – 8 US 3. Spule: 3 OS – 9 US 4. Spule: 4 OS – 10 US +6 -5 +6 -5 1 OS 7 US 2 OS 2 OS 8 US 3 OS 5. Spule: 5 OS – 11 US 6. Spule: 6 OS – 12 US 7. Spule: 7 OS – 1 US 8. Spule: 8 OS – 2 US 9. Spule: 9 OS – 3 US 10. Spule: 10 OS – 4 US UNTER-Schicht (US) 11. Spule: 11 OS – 5 US 12. Spule: 12 OS – 6 US 1. Spule: 1 OS – 7 US usw. in sich geschlossen TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/37 N-Pol Institut für Elektrische Energiewandlung • FB 18 Fertigung der Ankerspulen und des Kommutators Ankerspule: Unten: ungeformt Oben: geformt Läuferpaket unbewickelt: Einlegen der Ankerspulen: Isolation in Läufernuten 4-pol. Zweischichtwicklung Kommutator links Unter- und Oberschicht, u = 3 Anlöten der Ankerspulenenden an die Kommutatorsegmente: Ober- und Unterschicht-Spulenenden werden in die Schlitze der Kommutatorsegmente eingelötet Quelle: Fa. Brenner/Bürstadt, Deutschland TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/38 Institut für Elektrische Energiewandlung • FB 18 Einlegen der Zweischicht-Ankerspulen in keillose Nuten Nuten ohne Keile: Die Wicklung wird nur mit Glasfaserbandagen („Umfangsnuten“ im Blechpaket) bandagiert Vorteil: Geringere Nuthöhe = geringere Ankerstreuinduktivität = geringere Reaktanzspannung Vierpoliger Wickelkopf u = 3 Spulenseiten je Nut und Schicht Nc = 2 Windungen je Spule Quelle: Fa. Brenner, Bürstadt TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/39 Institut für Elektrische Energiewandlung • FB 18 Induzierte Ankerspannung (1) Maximale Spannung pro Spule: Mittlere Spannung pro Spule: U i,c,av 2va e B ,m Ncle Uˆ i,c 2va B ,m Ncle Fluss pro Pol: e ple B ,m Ankerumfangsgeschwindigkeit: 2 p p d si va d si n va 2 p p n U i,c,av 2 2 p Nc n Mittlere Spannung bei K/(2p) Spulen: ui ,av 2Nc Gesamtzahl der Ankerleiter: z 2 K N c ui ,av K 2p Pole, 2a parallele Zweige: TECHNISCHE UNIVERSITÄT DARMSTADT Ui,c,av 2 2 p p n e B ,m Ncle K 2 2 p N c n 2p ( 2 K N c ) n ui,av U i z n p U i z n a Prof. A. Binder : Elektrische Maschinen und Antriebe 10/40 Institut für Elektrische Energiewandlung • FB 18 Induzierte Spannung in der Ankerwicklung 2a 2 p "SCHLEIFENWICKLUNG„: Aus 2-poliger entsteht 6-polige (allgemein 2p-polige) Maschine durch identische Fortsetzung der Ankerwicklung, der Ständerpolfolge und der Bürstenanordnung Induzierte Spannung: U i z TECHNISCHE UNIVERSITÄT DARMSTADT k1 p z p k k n k1 n U i k2 m 1 2 a 2 a Prof. A. Binder : Elektrische Maschinen und Antriebe 10/41 Institut für Elektrische Energiewandlung • FB 18 Anzahl paralleler Zweige der Schleifenwicklung 2a = Anzahl paralleler Ankerwicklungszweige 2a = 2: Minimale Anzahl paralleler Zweige (bei 2p = 2) 2a = 2p: Stets sind Polzahl und Anzahl paralleler Zweige gleich a = p : Anzahl der positiven Kohlebürsten A a = p : Anzahl der negativen Kohlebürsten B 2a = 2p: Anzahl der Bürsten A und B ACHTUNG: Bei Drehfeldmaschinen: a = Anzahl paralleler Zweige je Wicklungsstrang, weil auch a = 1 (Serienschaltung) möglich TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/42 Institut für Elektrische Energiewandlung • FB 18 Vollständige eingängige Anker-Schleifenwicklung Statorpol Süd Kommutator Bürste 50 A Statorpol Nord 50 A 50 A Ic = 25 A Ia/a = 50 A 100 A Quelle: Dr. Holzer, TU Wien Beispiel: Eingängige vierpolige Schleifenwicklung: Daten: Qr = 26, 2p = 4, u = 1, Nc = 1, a = p = 2, K = 26, y1 = 6, y2 = 5, y = 1 TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/43 Ia = 100 A Institut für Elektrische Energiewandlung • FB 18 Eingängige Anker-Schleifenwicklung: 2a = 2p Beispiel: Qr = 26, 2p = 4, u = 1, Nc = 1, a = p = 2, K = 26, y1 = 6, y2 = 5, y = 1 Spule Nc = 1 10 V Anzahl der Pole = Anzahl der parallelen Wicklungszweige: 2a = 2p = 4 OS US Ua = 60V (= 6 . 10 V) Ia/a = 50 A P U i I a 60 100 6 kW Ia = 100 A -30 V +30 V Ia = 100 A „ 1 Gang“ TECHNISCHE UNIVERSITÄT DARMSTADT Quelle: Dr. Holzer, TU Wien Ic = Ia/(2a) = 25 A Prof. A. Binder : Elektrische Maschinen und Antriebe 10/44 Institut für Elektrische Energiewandlung • FB 18 Bürstenkurzschluss NUR der spannungslosen Spulen 13 19 Kommutator Bürste Spulenkurzschluss durch Bürste Beispiel: Spule 13 (OS)-19(US) liegt in neutraler Zone = keine Spannung induziert = kann von Bürste B2 gefahrlos kurzgeschlossen werden! Quelle: Dr. Holzer, TU Wien K = Qr = 26, 2p = 4, y1 = 6, y2 = 5, y = 1 TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/45 Institut für Elektrische Energiewandlung • FB 18 Reale E-Maschinen sind (leicht) unsymmetrische Maschinen! - Realität: Keine Maschine ist ideal symmetrisch. - Induzierte Spannungen je Pol sind von Pol zu Pol nicht exakt gleich groß. - Spannungsdifferenzen bewirken unsymmetrische Aufteilung des Ankerstroms Ia auf die parallelen Zweige. TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/46 Institut für Elektrische Energiewandlung • FB 18 Wirkung paralleler, ungleich großer Spannungen I Kommutator Beispiel: 2p = 2: Parallele Spannungsquellen mit ungleicher Quellenspannung, aber gleichem Innenwiderstand Ri: Beispiel: 2p = 2a = 2 I U0 + U Ri Bürste B I0 + I Bürste A U0 - U Ri I0 - I Generator, Erzeuger-Zählpfeilsystem R TECHNISCHE UNIVERSITÄT DARMSTADT Ia = 2I0 U1 U0 U U2 U0 U Der außen fließende Nutzstrom Ia wird vom Mittelwert U0 der beiden Spannungen getrieben! I a 2 I 0 U0 /( R 0.5 Ri ) Zusätzlich fließt ein innerer Kreisstrom I als Ausgleichsstrom zwischen beiden Spannungsquellen (der von deren Spannungsdifferenz 2U getrieben wird) über den Kommutator und nur quer über die Bürsten A, B! I 2U /( 2 Ri ) U / Ri Prof. A. Binder : Elektrische Maschinen und Antriebe 10/47 Institut für Elektrische Energiewandlung • FB 18 Ausgleichsströme belasten Bürstenkontakt! U0+U Ri B1 U0-U I0-I U0 I0 B2 U0 I0 I0+I Beispiel: Vierpolige Schleifenwicklung = vier parallele Wicklungszweige, 2p = 2a = 4! A1 Z. B.: Zwei Spannungszweige mit unterschiedlicher induzierte Spannung Ri Ri 2I0-I Ri R Ia = 4I0 Generator, Erzeuger-Zählpfeilsystem TECHNISCHE UNIVERSITÄT DARMSTADT A2 2I0+I Ausgleichsstrom fließt über parallele Bürsten A1 und A2 Bürste A2 wird elektrisch überlastet! Beispiel: I / 2I0 = 0.2, 2p = 2a = 4: Bürste A2 trägt 120%, Bürste A1 80 % des Nenn-Bürstenstroms A2 elektrisch überlastet, Bürstenlänge nimmt rasch ab; Bürste muss getauscht werden = HOHER Wartungsaufwand! Prof. A. Binder : Elektrische Maschinen und Antriebe 10/48 Institut für Elektrische Energiewandlung • FB 18 Ausgleichsverbinder übernimmt den Ausgleichsstrom U0+U B1 Ausgleichsverbinder I0 I I0 A1 U0-U I0-I U0 I0 B2 2I0 U0 Abhilfe: Ausgleichsverbinder 1. Art: Kupferleitungen, die Kommutatorlamellen mit (theoretisch) gleichem elektrischen Potential A2 2I verbinden. 0 - Der Ausgleichsstrom fließt innerhalb der Ankerwicklung und durch den Ausgleichsverbinder, belastet aber NICHT den thermisch empfindlichen Bürstenkontakt! I0 R Ia = 4I0 Beispiel: I / 2I0 = 0.2, 2p = 2a = 4: Ausgleichsstrom im Ausgleichsverbinder 20 % des Nenn-Bürstenstroms, fließt aber NICHT über den empfindlichen Bürstenkontakt. Generator, Erzeuger-Zählpfeilsystem TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/49 Institut für Elektrische Energiewandlung • FB 18 Ausgleichsverbinder 1. Art für die Schleifenwicklung „Ausgleichsverbinder-Schritt“: yV = K / p 80% 120% Ausgleichsverbinder 1. Art („Ausgleicher“) Hier: Nur jede dritte Spule an Ausgleichern angeschlossen, also 4 Ausgleicher TECHNISCHE UNIVERSITÄT DARMSTADT Beispiel: 2p = 4, 2a = 4, u = 2, Qr = 12, K = 12.2 = 24, Ausgleichsverbinder-Schritt: yV = K/p = 24/2 = 12 Lamelle 1 und 13 durch Ausgleicher 1. Art verbunden usw. Am besten: Alle Spulen an Ausgleicher angeschlossen, aber teuer; daher meist nur eine Spule je Nut an Ausgleichern angeschlossen z. B. bei u = 2 Spulen je Nut: Jede zweite (allg. u-te Spule) an Ausgleichern Prof. A. Binder : Elektrische Maschinen und Antriebe 10/50 Institut für Elektrische Energiewandlung • FB 18 Montage der Ausgleichsverbinder 1. Art Ausgleichsverbinder 1. Art für vierpolige Wicklung: Verbinder-Schritt = 2 Polteilungen = halber Umfang 100% 100% Ausgleichsverbinder 1. Art Quelle: Fa. Brenner, Bürstadt Ausgleichsverbinder 1. Art unter der Bandage TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/51 Institut für Elektrische Energiewandlung • FB 18 Beispiel: K = 26, 2p = 4: Ausgleichsverbinder 1. Art Ausgleichsverbinder-Schritt: yV = K/p Beispiel: yV = K/p = 26/2 = 13 Es kann z. B. Kommuatorsegment 10 mit 23 verbunden werden, weil sie theoretisch auf gleichem Potential liegen! Quelle: Dr. Holzer, TU Wien K = Qr = 26, 2p = 4, y1 = 6, y2 = 5, y = 1 TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/52 Institut für Elektrische Energiewandlung • FB 18 Wirkung der Ausgleichsverbinder 1. Art Hier: jede 2. Spule an Ausgleicher angeschlossen! Ausgleichsstrom 2 mit Ausgleichsverbinder Ausgleichsstrom 1 ohne Ausgleichsverbinder fließt über Bürsten A1, A2 Beispiel: yV = K/p = 26/2 = 13 K = Qr = 26, 2p = 4, y1 = 6, y2 = 5, y = 1 Quelle: Dr. Holzer, TU Wien a) Wenn Spulenseite 10 (S) und 23 (OS) auf Grund von Unsymmetrien nicht identisches Potential haben, treibt deren Potentialdifferenz einen Ausgleichsstrom 1, der auch über den Bürstenkontakt fließt und diesen zusätzlich thermisch belastet! b) Werden Ausgleichsverbinder zwischen Spule 10 und 23, 8 und 21 usw. angeordnet, so fließt der Ausgleichsstrom 2 intern über diese Ausgleichsverbinder und belastet die Bürsten NICHT! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/53 Institut für Elektrische Energiewandlung • FB 18 Die Wellenwicklung – Alternative zur Schleifenwicklung Oberschicht Unterschicht N OS S US S N OS US Ein Ankerspule als Grundelement Beispiel: 2a = 2, u = 1, Qr = 25, 2p = 4, K = 25, y1 = 6, y2 = 6 Wicklungsschritt y = (K-1)/p = 12 = y1 + y2 = 6 + 6: 1 (Oberschicht) 7 (Unterschicht) 13 (OS) 19 (US) 25 (OS) 6 (US)..., usw. TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/54 Institut für Elektrische Energiewandlung • FB 18 Entstehung der Wellenwicklung a) OS US OS US a) In Serie geschaltete “wellenförmige” Ankerspulen: - Bilden nach einem Anker-Umlauf NACH RECHTS einen “Wellenzug” - Anfang und Ende des Wellenzugs um eine Segmentteilung auseinander - Nach (K-1)/(2p) Wellenzügen ist die Hälfte aller OS und US belegt. z. B.: Start bei 7, Ende bei 1 b) b) Derselbe Vorgang NACH LINKS (= gestrichelt) füllt die restlichen OS und US: Die eingängige Wellenwicklung hat stets zwei parallele Zweige: a = 1, 2a = 2, unabhängig von der Polzahl ! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/55 Institut für Elektrische Energiewandlung • FB 18 Die Wellenwicklung – 2 Bürsten reichen, ABER …. - Nur eine Plus- und eine Minus-Bürste ausreichend, da nur zwei parallele Zweige. ABER: Großer Bürsten-Querschnitt nötig (= große Bürstenmasse: UNGÜNSTG) - Die von den Bürsten kontaktierten Spulen liegen in der neutralen Zone: es wird in ihnen keine Spannung induziert wird Beispiel: Bei 19 dasselbe Potential wie bei 7! - Daher: Man kann im Abstand der doppelten Polteilung weitere A-Bürste setzen und mit der ersten parallel schalten. Es erfolgt nur ein Kurzschluss spannungsloser Spulen (z. B.: zwischen Kommutatorsegment 7-19, 8-20 usw.): SOMIT: p Plus- und p Minusbürsten mit kleinem Querschnitt 1/p möglich. N - 50V TECHNISCHE UNIVERSITÄT DARMSTADT S +50V - 50V N S +50V +50V - 50V Prof. A. Binder : Elektrische Maschinen und Antriebe 10/56 +50V - 50V Institut für Elektrische Energiewandlung • FB 18 Die Wellenwicklung – keine Ausgleicher erforderlich - Die spannungslosen Spulen wirken als Ausgleicher 1. Art ( = sie verbinden gleiche Potentiale A1 und A2 bei 2p = 4). (Analog bei B1 und B2). Fazit: Die Wellenwicklung ist selbstausgleichend. N N A1 TECHNISCHE UNIVERSITÄT DARMSTADT B2 S Auf demselben Potential +50V +50V - 50V - 50V B1 S A2 Prof. A. Binder : Elektrische Maschinen und Antriebe 10/57 Institut für Elektrische Energiewandlung • FB 18 Vollständige eingängige Wellenwicklung 25 A 25 A Ia/a = 25 A 25 A 50 A Wellenwicklung: Beispiel: Quelle: Dr. Holzer, TU Wien Ia = 50 A Qr = 25, 2p = 4, u = 1, Nc = 1, a = 1, K = 25, y1 = 6, y2 = 6, y = 12 TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/58 Institut für Elektrische Energiewandlung • FB 18 Eingängige Anker-Wellenwicklung: 2a = 2 Beispiel: Qr = 25, 2p = 4, u = 1, Nc = 1, a = 1, p = 2, K = 25, y1 = 6, y2 = 6, y = 12 10 V Anzahl der parallelen Wicklungszweige STETS 2: 2a = 2 Ic = Ia/(2a) = 25 A Ua = 100 V 100 50 5 kW (= 10 . 10 V) +50 V -50 V Ia = 50 A Ia = 50 A „ 1 Gang“ TECHNISCHE UNIVERSITÄT DARMSTADT P U i I a Ic = Ia/(2a) = 25 A Prof. A. Binder : Elektrische Maschinen und Antriebe 10/59 Quelle: Dr. Holzer, TU Wien Institut für Elektrische Energiewandlung • FB 18 Eingängige Wellenwicklung: Zwei parallele Zweige = kein Ausgleichsstrom über die Bürsten I Kommutator 2p 2, 2a = 2: 2a = 2: Zwei parallele Spannungsquellen mit i. A. etwas ungleicher Quellenspannung, aber z. B. gleichem Innenwiderstand Ri: I U0 + U Ri Bürsten B I0 + I Bürsten A U0 - U Ri I0 - I Generator, Erzeuger-Zählpfeilsystem R TECHNISCHE UNIVERSITÄT DARMSTADT Ia = 2I0 U1 U0 U U2 U0 U Nutzstrom Ia durch den Mittelwert U0 fließt über die Bürsten! I a 2 I 0 U0 /( R 0.5 Ri ) Ausgleichsstrom fließt als innerer Kreisstrom I zwischen beiden Parallelzweigen (von 2U getrieben) über den Kommutator, aber nicht über die Bürsten A, B! I 2U /( 2 Ri ) U / Ri Prof. A. Binder : Elektrische Maschinen und Antriebe 10/60 Institut für Elektrische Energiewandlung • FB 18 Schleifenwicklung Oberschicht Unterschicht Spule Nc = 1 Wellenwicklung Oberschicht Unterschicht symmetrisch Oberschicht Unterschicht TECHNISCHE UNIVERSITÄT DARMSTADT Spule Nc > 1 Oberschicht Unterschicht Prof. A. Binder : Elektrische Maschinen und Antriebe 10/61 Oberschicht Unterschicht unsymmetrisch Ein Ankerspule als Grundelement Institut für Elektrische Energiewandlung • FB 18 Segmentspannung - Überschlagsgefahr Mittlere Segmentspannung: U s,av Ua p 2 N c va le B ,av K /( 2 p) a Lokale Segmentspannung bei Ia = 0: U s,max U s,av B ,m B ,av U s,av e Zulässige Grenzwerte: Us,av < 20 V, Us,max < 35 V Beispiel: p/a = 1, K/(2p) = 6, Ua = 100 V Mittlere Segmentspannung: U s,av 100V/6 17V 20V Lokale Segmentspannung: Us,max = 17 V/ 0.6 = 28 V < 35 V ( 20 V/0.6) TECHNISCHE UNIVERSITÄT DARMSTADT Us,av = 17 V Ua = 100 V Prof. A. Binder : Elektrische Maschinen und Antriebe 10/62 Institut für Elektrische Energiewandlung • FB 18 Vergleich: Schleifen- und Wellenwicklung z p Ui n a Schleifenwicklung Wellenwicklung Anzahl parallele Zweige = Polzahl Anzahl parallele Zweige stets 2 2a = 2p 2a = 2 Ausgleicher 1. Art erforderlich selbstausgleichend Hohe Ströme möglich, weil viele parallele Strom begrenzt auf ca. 500 A, da max. Zweige ca. 250 A / Parallelzweig Spannung steigt proportional z Hohe Spannung, da diese proportional z.p steigt. Hohe Leistung möglich (bis ca. 12 MW) Leistung begrenzt (ca. 300 kW) Große Leistung: ausschließlich mit Schleifenwicklung Kleine Leistung: meist Wellenwicklung: billiger (keine Ausgleichsverbinder), viele Serienleiter: ausreichend hohe Spannung trotz des kleinen Flusses Beispiel: 6 MW-Walzwerksantriebe mit 18 Polen: Schleifenwicklung: 18 parallele Ankerwicklungszweige TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/63 Institut für Elektrische Energiewandlung • FB 18 Beispiel: Induzierte Ankerspannung • Induzierte Spannung: z p 1 zp Ui n 2n k2 m a 2 a Merkformel: U i k 2 m • Maschinenkonstante: k2 • Beispiel 1: 1 z p 2 a z = 900 Leiter, 2p = 4 Pole, 2a = 4 parallele Zweige: k2 • 1 900 2 143.2 2 2 Beispiel 2: n = 4500/min, = 0.008 Wb: Ui = 143.2.(2.4500/60).0.008 = 540 V TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/64 Institut für Elektrische Energiewandlung • FB 18 Grosse hochpolige fremderregte Gleichstrommaschine Schleifenwicklung 2.7m-WalzwerksGrobgerüst-TandemAntrieb 2 x 6 = 12 MW n = 50 … 100/min M = 1146 … 573 kNm 2p = 18 = 2a Ua = 1300 V Ia = 4870 A Ia/(2a) = 270 A K = 1638, dsi = 4.2 m le = 0.8 m, dC = 2.9 m Kommutator Us,av = 1300 V/91 = 14.3 V < 20 V K/(2p) = 91 Weltgrößter WalzwerksZwillingsumkehrmotor 2 x 12 785 kW 90 … 150/min 1357 …814 kNm 2p = 2a = 18 Zweite Gleichstrommaschine S N S Quelle: Siemens AG Quelle: ELIN-Union AG TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/65 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe Zusammenfassung: Ankerwicklungen - Läuferwicklung: Schleifen- oder Wellenwicklung (eingängig) - Mehrgängige Wicklungen veraltet (nicht mehr im Einsatz) - Schleifenwicklung: Polzahl = parallele Wicklungszweigzahl - Wellenwicklung: Nur zwei parallele Zweige - Schleifenwicklung: für große Ströme und Leistungen = große Maschinen - Wellenwicklung: für kleinere Maschinen bis ca. 300 kW TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/66 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe 10. Gleichstromantriebe 10.1 Die Funktionsweise der Gleichstrommaschine 10.2 Ankerwicklungen 10.3 Induzierte Spannung und elektromagnetisches Drehmoment 10.4 Ankerrückwirkung und Kompensationswicklung 10.5 Kommutierung des Ankerstroms und die Funktion der Wendepole 10.6 Generator- und Motorschaltungen der Gleichstrommaschine 10.7 Der drehzahlveränderbare Gleichstromantrieb 10.8 Leistungsgrenzen der Gleichstrommaschine TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/67 Institut für Elektrische Energiewandlung • FB 18 Induzierte Spannung = Leerlaufkennlinie (Generator) Ui-Veränderung über n und If Eisensättigung U a0 (n = konst.) Leerlaufkennlinie: Ua0 = Ui (n = konst.) Generatorisch gemessene Ankerspannung URem p U i z n ( I f ) k1 n a - Induzierte Spannung Ui steigt LINEAR mit Drehzahl n - Induzierte Spannung steigt LINEAR mit Fluss - Eisensättigung: Fluss steigt nichtlinear mit Feldstrom If Remanenzspannung - Feldstrom abgeschaltet: If = 0: Es verbleibt Remanenzflussdichte BRem im Statoreisen; induziert kleine Remanenzspannung URem - Von außen an den Bürsten externe Spannung U > Ui angelegt: U U i I a Ra U b Es fließt Gleichstrom (Ankerstrom) Ia - Ankerwicklungswiderstand Ra und Bürstenspannungsfall Ub (ca. 2V) sind klein ! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/68 Institut für Elektrische Energiewandlung • FB 18 Beispiel: Gleichstrommaschinenparameter • • • • • • • • • Rotor = Läufer = Anker, Stator = Ständer Windungszahl je Ankerspule: Nc (z. B.: 5), ideelle Polbedeckung: z.B.: e = 0.7 Fluss pro Pol: e p lB ,m z.B: B,m = 0.95 T, Polteilung p = 0.1 m, Länge l = 0.12 m, daher 0.7 0.1 0.12 0.95 0.008Wb Anzahl der Spulenseiten je Rotornut 2u (z. B. u = 3) Anzahl der Rotornuten Q (z. B. 30) Anzahl der Kommutatorlamellen und Ankerspulen: K = Q.u (z. B. 30.3 = 90) Anzahl der Leiter am Ankerumfang: z = K.Nc.2 (z.B.: 90.5.2 = 900) Anzahl der Pole 2p = Anzahl der parallelen Ankerzweige 2a (z. B. 4) Ankerumfang: 2 p p d si (z. B. 4.0.1 m = 0.4 m, dsi = 127.3 mm), Ankerumfangsgeschwindigkeit: va 2 p p n : va = 0.4.(4500/60) = 30 m/s = 108 km/h TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/69 Institut für Elektrische Energiewandlung • FB 18 Beispiel: Anker einer 200 kW-Gleichstrommaschine Angaben: Anker-Nennspannung 430 V, Nenndrehzahl n = 1470/min, Ankerdurchmesser dr = 400 mm, Polzahl 2p = 4, Ankerlänge le = 190 mm, Qr = 58 Nuten, Spulenseiten je Nut & Schicht u = 4, Windungszahl/Spule Nc = 1, äquivalente Polbedeckung e = 0.7, maximale Luftspaltflussdichte: B,m = 0.86 T, Schleifenwicklung 2a = 4 Berechnungen: - Anzahl der Kommutatorsegmente K = Qr . u = 58.4 = 232 - Gesamtleiterzahl z = 2 . K . Nc = 2 . 232 . 1 = 464 - Polteilung p = dsi . /4 = 400 /4 = 314.2 mm (dr dsi) - Hauptfluss pro Pol = e.p.le.B,m = 0.7 . 0.3142 . 0.19 . 0.86 = 35.9 mWb - Induzierte Spannung Ui = z . (p/a) . n . = 464 . (2/2) . (1470/60) . 0.0359 = 408.5 V • Mittlere Segmentspannung zwischen zwei Kommutatorsegmenten bei Nenndrehzahl 408.5/(232/4) = 7 V < 18 ... 20V (sonst Überschlag zwischen den Segmenten !) Zwischen den Segmenten 0.3 mm Glimmer als Isolation, aber Luftstrecke parallel ! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/70 Institut für Elektrische Energiewandlung • FB 18 Der Bürstenkontakt Graphit-Bürste 100% Quelle: Schunk Kohlenstofftechnik, Giessen 80% Bürstenübergangswiderstand (= in der Bürsten-Gleitzone) - Bürstenspannungsfall für A- und B-Bürste: Ub = UA + UB = ca. 2 V - Bürstenspannungsfall Ub: - steigt nichtlinear mit der Bürstenstromdichte Jb - sinkt mit steigender Temperatur. - Zul. Bürsten-Stromdichte Jb: ca. 1/100 der Spulen-Stromdichte (< 10 A/cm2) TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/71 Institut für Elektrische Energiewandlung • FB 18 Kommutator und Graphitbürsten Kommutator-Lamellen Isolation (Glimmer) Bürstenhalter (Messing) Stromseile 5 Graphitbürsten parallel je Bürstenhalter Federdruck Kommutatorstegteilung ca. 3 mm im Minimum Quelle: Fa. Brenner, Bürstadt TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/72 Glimmerisolierung ca. 0.3 mm Institut für Elektrische Energiewandlung • FB 18 Elektromagnetisches Drehmoment e e I Pro Pol existiert nur eine Stromrichtung. Strom teilt sich auf 2a parallelen Zweige: I c a 2a In der Ankerwicklung: Wechselstrom ic je Spule, außen: Gleichstrom Ia Gleichsinnige Kraft auf die Ankerleiter im Luftspaltfeld B : Fc I c B le Mittlere Kraft pro Leiter: Fc,av I c e B ,mle Hebelarm d r / 2 d si / 2 p p / p p I a z ( p / a) e B ,mle I a e ple B ,m Drehmoment bei z Leitern: M e z 2a 2 TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/73 Institut für Elektrische Energiewandlung • FB 18 Drehmomentformel p p I a z ( p / a) Me z e B ,mle I a e ple B ,m 2a 2 k2 Ia M e k 2 I a Nicht verwechseln mit Formel für induzierte Spannung ! U i k2 m TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/74 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe Zusammenfassung: Induzierte Spannung und elektromagnetisches Drehmoment - Induzierte Spannung prop. zu Drehzahl und Ständerfluss/Pol - El.-magn. Drehmoment prop. zu Ankerstrom und Ständerfluss/Pol - Bürstenkontakt: Elektrisch nichtlinear, etwa 2 V Spannungsfall TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/75 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe 10. Gleichstromantriebe 10.1 Die Funktionsweise der Gleichstrommaschine 10.2 Ankerwicklungen 10.3 Induzierte Spannung und elektromagnetisches Drehmoment 10.4 Ankerrückwirkung und Kompensationswicklung 10.5 Kommutierung des Ankerstroms und die Funktion der Wendepole 10.6 Generator- und Motorschaltungen der Gleichstrommaschine 10.7 Der drehzahlveränderbare Gleichstromantrieb 10.8 Leistungsgrenzen der Gleichstrommaschine TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/76 Institut für Elektrische Energiewandlung • FB 18 Kraftbildung aus dem Feldlinienbild erkennbar • • Überlagerung des Eigenfelds der Ankerleiter mit dem Erregerfeld der Hauptpole ergibt resultierendes Magnetfeld. Flussröhren zwischen den Feldlinien wirken wie “Gummischnüre” (MAXWELL´scher Magnetzug) und drehen den Läufer im Gegen-Uhrzeigersinn (MOTOR-Betrieb). TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/77 Institut für Elektrische Energiewandlung • FB 18 Feldverzerrung durch das Ankerfeld Ia = 0 : Luftspaltfeld B0 bei Leerlauf (Ankerstrom = 0) unter dem Pol annähernd konstant, da konstanter Luftspalt . Vf B ( x ) 0 für Fe ( x) Ia > 0 : Bei Last (Ankerstromfluss) entsteht zusätzlich das Ankerfeld Ba. Es überlagert sich "quer" zum Hauptfeld und verzerrt es (Ankerrückwirkung). B ( x) 0 V f Va ( x) ( x) für Fe - Linke Polhälfte: B = B0 – Ba - Rechte Polhälfte: B = B0 + Ba TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/78 Institut für Elektrische Energiewandlung • FB 18 Flussverringerung durch die Ankerrückwirkung - Die Feldzunahme in der rechten Polhälfte treibt das Eisen in Sättigung. Fe - Daher gilt rechts nicht B = B0 + Ba, sondern: B < B0 + Ba. - Wegen der Eisensättigung rechts ist die Flusszunahme rechts geringer als die Abnahme links, so dass insgesamt pro Pol ein Flussverlust auftritt. ( I a 0) ( I a 0) ( I a 0) Zusätzliche Sättigung TECHNISCHE UNIVERSITÄT DARMSTADT Fazit: Mit steigendem Ankerstrom Ia sinkt der Fluss pro Pol (TROTZ konstanten Erregerstroms If). Prof. A. Binder : Elektrische Maschinen und Antriebe 10/79 Institut für Elektrische Energiewandlung • FB 18 Abhilfe gegen Ankerrückwirkung: Kompensationswicklung Anker Kompens H d s a Anker Kompens 0 C Schaltung der Wendepol- und der Kompensationswicklung in Serie zur Ankerwicklung Von Ia durchflossene Kompensationswicklung in den Ständerpolen Wickelsinn entgegengesetzt zur Ankerwicklung: Durchflutungen von Anker- und Kompensationswicklung heben sich auf: Ba = 0Ha = 0 TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/80 Institut für Elektrische Energiewandlung • FB 18 Kompensierte vierpolige Gleichstrommaschine Feldspule Kompensationswicklung Wendepolwicklung Ankerwicklung Quelle: ABB, Schweden Feldliniendichte links und rechts gleichmäßig = KEINE Feldverzerrung ! Kompensationswicklung erforderlich ab ca. 200 … 300 kW ! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/81 Institut für Elektrische Energiewandlung • FB 18 Gleichstrommaschine – Ständerpole unbewickelt Hauptpol mit Nuten für Kompensationswicklung Wendepol Quelle: Fa. Brenner, Bürstadt TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/82 Institut für Elektrische Energiewandlung • FB 18 Bewickelte Ständerpole – vierpolig Erregerwicklung Kompensationswicklung N K ,Pol 3 (2 4) 24 Wendepolwicklung Quelle: Fa. Brenner, Bürstadt TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/83 Institut für Elektrische Energiewandlung • FB 18 Unkompensierte Maschine: Maximale Segmentspannung bei Nennstrom Nennpunkt Feldschwächung N, IaN, nN, vN U s (x ) Anker-Spulenseite vN U s U i,c 2 Nc v le B ( x) B,max = 1.2 T Leer Last v* = 2vN U s,av ~ vN B ,av , U s,av 20V U s,max ~ vN B ,max , U s,max (1.2 / 0.8) 20 30V 35V B*,max = 0.9 T KEINE Sättigung durch ARW B* = 0.5 T B*,av = 0.4 T B,min = 0.6 T p TECHNISCHE UNIVERSITÄT DARMSTADT U s* ( x ) Sättigung durch ARW B = 1.0 T B,av = 0.8 T Luftspaltfeld N/2, IaN, 2nN, 2vN (p/a = 1) x B*,min = 0.1 T U s,av ~ 2vN B*,av , U s*,av 20V U s*,max (0.9 / 0.4) 20 45V 35V Kompensationswicklung erforderlich ! Prof. A. Binder : Elektrische Maschinen und Antriebe 10/84 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe Zusammenfassung: Ankerrückwirkung und Kompensationswicklung - Eigen-Magnetfeld des Läufers überlagert sich dem Ständerfeld - Resultierendes Feld im Luftspalt „verzerrt“ mit Feldüberhöhung - Kompensationswicklung in Ständerpolen hebt das Läuferfeld auf = = KEINE Feldverzerrung TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/85 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe 10. Gleichstromantriebe 10.1 Die Funktionsweise der Gleichstrommaschine 10.2 Ankerwicklungen 10.3 Induzierte Spannung und elektromagnetisches Drehmoment 10.4 Ankerrückwirkung und Kompensationswicklung 10.5 Kommutierung des Ankerstroms und die Funktion der Wendepole 10.6 Generator- und Motorschaltungen der Gleichstrommaschine 10.7 Der drehzahlveränderbare Gleichstromantrieb 10.8 Leistungsgrenzen der Gleichstrommaschine TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/86 Institut für Elektrische Energiewandlung • FB 18 Kommutierung (Stromwendung) des Ankerstroms Ankerspulenstrom ic ist Wechselstrom. ic wechselt zwischen positiven Wert Ia/(2a) und negativen Wert -Ia/(2a), wenn die Bürste die beiden Spulenanschlüsse ( = benachbarte Kommutatorsegmente) kurz schließt. Dabei befinden sich die beiden Spulenseiten in der „neutralen Zone“ (B = 0). Es wird keine Spannung in sie induziert (Ui,c = 0). Ankerdrehrichtung TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/87 Institut für Elektrische Energiewandlung • FB 18 Kommutierung (Stromwendung) des Ankerstroms vC d C n Ankerspule hat Induktivität Lc (Nut- und Stirnstreufeld). Stromänderung bewirkt Selbstinduktionsspannung (“Reaktanzspannung”) uR. Näherung: "lineare Kommutierung": k R Lc d C /(a bb ) dic Ia u R Lc Lc k R nI a dt aTcom TECHNISCHE UNIVERSITÄT DARMSTADT Tcom bb / vC ~ 1 / n Prof. A. Binder : Elektrische Maschinen und Antriebe 10/88 uR k R n I a Institut für Elektrische Energiewandlung • FB 18 Einlegen der Zweischicht-Ankerspulen in keillose Nuten Nuten ohne Keile: Die Wicklung wird nur mit Glasfaserbandagen („Umfangsnuten“ im Blechpaket) bandagiert Vorteil: Geringere Nuthöhe = geringere Ankerstreuinduktivität = geringere Reaktanzspannung uR Vierpoliger Wickelkopf u = 3 Spulenseiten je Nut und Schicht Nc = 2 Windungen je Spule Quelle: Fa. Brenner, Bürstadt TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/89 Institut für Elektrische Energiewandlung • FB 18 Schädliche Reaktanzspannung uR uR k R n I a uR steigt a) mit Belastung der Maschine (prop. M bzw. Ia) b) mit Drehzahl n. uR "zündet" Abschaltfunken (Funkenenergie Lc ic2 / 2) zw. Bürste und Kommutatorlamelle („Bürstenfeuer“) rasche Erosion der Bürsten Bürstenlänge nimmt ab Bürstentausch nötig ! vC uR TECHNISCHE UNIVERSITÄT DARMSTADT Bürstenfeuer an der ablaufenden Bürstenkante Prof. A. Binder : Elektrische Maschinen und Antriebe 10/90 Institut für Elektrische Energiewandlung • FB 18 Wendepole zur Aufhebung der Reaktanzspannung uR Wendepole in Pollücken mit Wendepolwicklung (Windungszahl NW,Pol, Ankerstrom Ia) Wendepolfeld BW induziert (Bewegungsinduktion) in kommutierende Ankerspule Wendefeldspannung uW uW ist zur Reaktanzspannung uR entgegengesetzt und hebt sie auf: uW = -uR ! 2 N c (va BW ) ds 2 N c va le BW le uW 0 und va d r n, BW ~ I a uW kW n I a Ziel: uR uW 0 Schaltung der Wendepolwicklung B1-B2 in Serie zum Anker A1-A2 mit entgegengesetztem Wicklungssinn TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/91 Institut für Elektrische Energiewandlung • FB 18 Dimensionierung der Wendepolwicklung uR und uW hängen von n und Ia ab: für JEDEN Betriebspunkt (n, Ia) erfüllbar: kW = kR. uR uW (k R kW ) n I a 0 Wendepolerregerdurchflutung W: Wendepol-Eisenkreis muss ungesättigt sein ! H ds 2H ,W W 2W 2a f f 2(W a ) C BW NW , Pol I a N a, Pol I a W a 0 0 ~ Ia W W uW kW n I a kW 2 N c 0 le dr W ( NW , Pol N a , Pol ) Wendepoldurchflutung: NW ,PolI a Ankerdurchflutung: N a,PolI a BW 0 TECHNISCHE UNIVERSITÄT DARMSTADT I z z a Ia 2 2 p 2a 8ap W a W 1 0 a (0.1...0.12) 0 a W W W a Prof. A. Binder : Elektrische Maschinen und Antriebe 10/92 Institut für Elektrische Energiewandlung • FB 18 Schaltung der Wendepolwicklung - Wendefeld muss Ankerfeld entgegen wirken - Daher: Entgegengesetzter Wicklungssinn 110% 10% 100% Wendefeld Ankerfeld Resultierendes Wendefeld NW , Pol W 1.1...1.12 a N a, Pol Für kW = kR müssen W und NW,Pol/Na,Pol richtig gewählt werden. Optische Überprüfung, ob die Bürsten “feuern” Falls Bürsten feuern: Wendefeld zu stark/zu schwach = "Über-/Unterkommutierung" Entfernen/Einbringen von Unterlegblechen am Wendepol vergrößert/verkleinert den Wendepolluftspalt W und verringert/erhöht daher das Wendefeld TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/93 Institut für Elektrische Energiewandlung • FB 18 Wendepole in einer vierpoligen Gleichstrommaschine Anbringen von Unterlegblechen Feldspule Kompensationswicklung Wendepolwicklung Ankerwicklung Quelle: ABB, Schweden Wendepole erforderlich ab ca. 1 kW ! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/94 Institut für Elektrische Energiewandlung • FB 18 Wendepole in einer vierpoligen Gleichstrommaschine Quelle: ABB, Schweden TECHNISCHE UNIVERSITÄT DARMSTADT Schaltung der Wendepol- und der Kompensationswicklung in Serie zur Ankerwicklung Prof. A. Binder : Elektrische Maschinen und Antriebe 10/95 Institut für Elektrische Energiewandlung • FB 18 Beispiel: Fremderregte Gleichstrommaschine Vierpolige Gleichstrommaschine - mit Wendepolen - ohne Kompensationswicklung Fremdlüfter mit 2poligem Asynchronantrieb 400 V, 260 A, 100 kW, 2000/min Achshöhe 160 mm a 100000 96.15% *) 400 260 Wellenende Klemmenkasten 160 mm Quelle: Siemens AG, Bad Neustadt/Saale, Deutschland Kühlluftaustritt TECHNISCHE UNIVERSITÄT DARMSTADT *) ohne Erregerverluste 700 W,res 95.51% Prof. A. Binder : Elektrische Maschinen und Antriebe 10/96 Institut für Elektrische Energiewandlung • FB 18 Ersatzschaltbild der fremderregten Gleichstrommaschine Ankerleiter, Wendepol- u. Kompensationswicklung = gesamter Ankerwiderstand Ra. Fremderregung: Erregerstrom If unabhängig von Ia einstellbar. U Ra I a U b Ui , Ui k2 m ( I f ) VerbraucherZählpfeilsystem Ub: Bürstenspannungsfall ca. 2 V, Ub oft vernachlässigt, wenn Ub/U << 1, z. B. bei U = UN 100V Bremsende Läuferverluste: Ummagnetisierungsverluste, Reibungsverluste, Zusatzverluste (Wechselstrom-Skineffekt) werden VERNACHLÄSSIGT! Innere Leistung P: Die Luftspaltleistung P wird über die LORENTZ-Kräfte in mechan. Leistung Pm (elektromagnetisches Drehmoment Me) umgesetzt. P Ui I a m M e Pm M e Ui I a / m (k2 m / m ) I a k2 I a TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/97 Institut für Elektrische Energiewandlung • FB 18 Beispiel: Leistungsbilanz eines Gleichstrommotors 200 kW-Motor, U = 430 V, n = 1470/min, a = 92% (Anker-Wirkungsgrad), Ui = 408.5 V - Zugeführte elektrische Leistung: Pe,in Pm,out / a 200 / 0.92 217.4kW U I a - Ankerstrom: I a Pe,in / U 217400/ 430 506A - Innere Leistung: P U i I a 408.5 506 206.7kW Pm ! Bremsende Läuferverluste bewirken: Pδ > Pm - Elektromagnetisches Drehmoment: Me = 206.7/(2 . 1470/60) = 1343 Nm - Drehmoment an der Welle: MM = Pm,out/m = 200/(2 . 1470/60) = 1299 Nm TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/98 Institut für Elektrische Energiewandlung • FB 18 Beispiel: Verlustbilanz der Gleichstrommaschine 200 kW-Gleichstrommotor fremderregt, Ia = 506 A, Ra = 37.9 m, PCu ,a Ra I a2 9.7kW A: Gesamte Läuferverluste 17.4 kW 1. Ankerkreisverluste 217.4 - 206.7 = 10.7 kW: 1.1 Bürsten: 2V . 506A = 1.0 kW 1.0 kW 1.2 Ankerwiderstand: PCu,a Pd ,a Pb 10.7 1.0 9.7kW 9.7 kW 2. Sonstige Läuferverluste durch mechanisch bremsendes Verlustmoment Md (= Differenz zwischen elektromagnetischem und Wellen-Moment): Md = Me – MM = 1.343 -1.299 = 0.044 kNm, PFe PR PZ 2nM d P Pm,out 206.7 200 6.7kW 2.1 Ummagnetisierungsverluste PFe: Wirbelstrom- und Hystereseverluste im geblechten Eisenkern des Läufers 2.2 Zusatzverluste PZ: Wirbelströme in den Nutenleitern durch Stromverdrängung, da im Leiter Wechselstrom fließt 10.7 kW 6.7 kW 2.3 Reibungs- und Ventilationsverluste PR (Lager, Bürsten, Kühlluftstrom) B: Erregerverluste Pf = Uf.If = 1.5 kW C: Gesamtverluste: 17.4 + 1.5 = 18.9 kW TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/99 1.5 kW 18.9 kW Institut für Elektrische Energiewandlung • FB 18 Stationäre Grundgleichungen der fremderregten Gleichstrommaschine Verbraucher-Zählpfeilsystem U I a Ra U i Erzeuger-Zählpfeilsystem U i I a Ra U Im Verbraucher-Zählpfeilsystem: U U a I a Ra U i (U b ) U i k 2 m ( I f ) U f Rf I f M e k 2 I a ( I f ) Me MM • Vernachlässigung der Reibungs-, Ummagnetisierungs-, Zusatzverluste im Läufer: Md = 0 • Wellenmoment MM inneres Moment Me TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/100 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe Zusammenfassung: Kommutierung des Ankerstroms und die Funktion der Wendepole - Läuferstrom = Wechselstrom. Sein Eigenfeld induziert „Reaktanzspannung“ in Läuferspule bei Stromwendung - Reaktanzspannung ergibt Schaltfunken an den Bürsten = „Bürstenfeuer“ - Wendepolwicklung in den Hauptpollücken induziert Gegenspannung („Wendefeldspannung“ hebt Reaktanzspannung auf = KEIN Bürstenfeuer) - Ersatzschaltbild der Gleichstrommaschine erfasst i. A. nur Verluste im Ankerkreis TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/101 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe 10. Gleichstromantriebe 10.1 Die Funktionsweise der Gleichstrommaschine 10.2 Ankerwicklungen 10.3 Induzierte Spannung und elektromagnetisches Drehmoment 10.4 Ankerrückwirkung und Kompensationswicklung 10.5 Kommutierung des Ankerstroms und die Funktion der Wendepole 10.6 Generator- und Motorschaltungen der Gleichstrommaschine 10.7 Der drehzahlveränderbare Gleichstromantrieb 10.8 Leistungsgrenzen der Gleichstrommaschine TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/102 Institut für Elektrische Energiewandlung • FB 18 Fremderregter Gleichstromgenerator - Kennlinien Leerlaufkennlinie Innere Kennlinie ErzeugerZählpfeilsystem ! Belastungskennlinie n = konst. - Maschine mit n = konst. angetrieben - Erregerwicklung F1-F2 aus fremder Gleichspannungsquelle Uf gespeist - If über Feldstell-Widerstand verändert 0 0 Remanenzspannung URem vernachlässigt Leerlaufkennlinie: Leerlaufspannung U0(If) U 0 k1 n ( I f ) Innere Kennlinie: bei unkompensierter Maschine sinkt der Polfluss infolge Sättigung durch Ankerrückwirkung mit steigendem Ankerstrom um den Wert : U i ( I f , I a ) k1 n ( I f , I a ) U 0 Belastungskennlinie: Ankerspannung U(If) in Abhängigkeit von If bei Ia = konst. U ( I f , I a ) U i ( I f , I a ) I a Ra U b TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/103 Institut für Elektrische Energiewandlung • FB 18 Ankerrückwirkung bei unterschiedlichem Erregerstrom Unkompensierte GSM Flussverlust pro Pol: 0 n = konst. 0 B B -ep/2 0 + ep/2 x 0 + = - - + - B x + x 0 Sättigung Sättigung If klein, keine Eisensättigung - = +: = 0 If Nennwert, mittlere Eisensättigung - > +: > 0 If groß, hohe Eisensättigung - = +: = 0 KEIN Flussverlust: Ui = U0 Flussverlust tritt auf: Ui < U0 KEIN Flussverlust: Ui = U0 TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/104 Institut für Elektrische Energiewandlung • FB 18 Fremderr. GS-Generator: Belastungskennlinie Innere Kennlinie Leerlaufkennlinie Belastungskennlinie 0 0 Kompensierte Maschine: Leerlaufkennlinie = Innere Kennlinie Unkompensierte Maschine: Leerlaufkennlinie Innere Kennlinie TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/105 Institut für Elektrische Energiewandlung • FB 18 Fremderr. GS-Generator: Äußere Kennlinie Erzeuger-Zählpfeilsystem ! Kompensierte Maschine 0 n = konst. 0 Äußere Kennlinie: Ankerspannung in Abhängigkeit von Ia bei If = konst. U ( I f , I a ) U i ( I f , I a ) I a Ra U b TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/106 Institut für Elektrische Energiewandlung • FB 18 Nebenschluss-/Fremderregter Gleichstrommotor (1) VerbraucherZählpfeilsystem ! n n0 U = konst. 0 M e Ra k1k2 2 0 Motorkennlinie n(M): kompensierter Motor Maschine mit U = konst. gespeist Erregerstrom If frei einstellbar U U i I a Ra (U b ), U i k1n Nebenschluss: Klemmen: E1-E2, an U Fremderregt: Klemmen: F1-F2: Fremde Uf-Quelle n U i U I a Ra M R k1 k1 Leerlauf: Motor nur durch eigenes kleines Verlustmoment Md (Reibung, Ummagnetisierungsverluste) gebremst: Me = Md 0. Leerlaufdrehzahl: TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/107 n n0 e a k1k 2 2 n0 U /( k1 ( I f )) Institut für Elektrische Energiewandlung • FB 18 Nebenschluss-/Fremderregter Gleichstrommotor (2) Fremderregter und Nebenschlussmotor haben - eine fallende Drehzahl-Drehmoment-Kennlinie - mit flacher Neigung, da der Ankerspannungsfall im Verhältnis zur Klemmenspannung klein ist („steife“ Kennlinie = Nebenschlussverhalten!) STABIL INSTABIL unkompensierte Maschine kompensierte Maschine (stets STABIL) 0 0 TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/108 Institut für Elektrische Energiewandlung • FB 18 Instabilität beim Nebenschluss-/fremderregten GS-Motor Unkompensierte Maschine: Hauptfluss sinkt etwa ab Nennstrom Ia = IN auf ´ = - (wegen zusätzlicher Sättigung durch Ankerrückwirkung) Bei großem Ia ist groß: Drehzahl steigt wieder an INSTABILITÄT (1. Term in der Gleichung stärker steigt als der 2. Term) m Ra M e U 2 k 2 ( ( I a )) k 2 ( ( I a ))2 STABIL INSTABIL Stabilitätsbedingung (Herleitung bei ASM): dM e dM s 0 stabil d m d m Stabilitätsgrenze Beispiel: INSTABIL: Drehzahlzunahme bei steigender Belastung: Maschine “geht durch”, sie beschleunigt ungebremst auf hohe Drehzahlen bis zur Selbstzerstörung. Abhilfe: Kompensationswicklung TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/109 Institut für Elektrische Energiewandlung • FB 18 Instabilität bei überkommutierendem Motor (Kurve 3) Überkommutierung: Stromwendung zu rasch INSTABIL 0 0 0 Kommutierende Spule hat durch Überkommutierung bereits die umgekehrte Spulendurchflutung und erregt Spulenfluss ~ Ia, der dem Hauptfluss entgegenwirkt ( - ) und diesen daher schwächt INSTABILITÄT Da ~ Ia schon bei kleinsten Strömen schwächend auftritt, kann die Drehzahlkennlinie schon ab dem Leerlauf ansteigen (Kurve 3) m Abhilfe: Wendefeld schwächen TECHNISCHE UNIVERSITÄT DARMSTADT Ra M e U 2 k 2 ( ( I a )) k 2 ( ( I a ))2 Prof. A. Binder : Elektrische Maschinen und Antriebe 10/110 Institut für Elektrische Energiewandlung • FB 18 Anlasswiderstand im Ankerkreis zum Anfahren (1) Motorstillstand: n = 0: Induzierte Spannung ist Null: Ui = 0 U U i I a Ra 0 I a Ra I a U / Ra Ankerwiderstand ist (außer bei Kleinmotoren) sehr klein: Ankerstrom im Stillstand SEHR GROSS: Motorwicklung würde verbrennen ! Abhilfe: Strombegrenzender Anlass-Widerstand im Ankerkreis: Dient zum Anfahren des Motors mit Nennstrom. ( RAnlasser Ra ) I N U RAnlasser U Ra IN Nach dem Anfahren begrenzt die induzierte Spannung den Strom; der Anlasser wird kurz geschlossen, um nicht unnötig Stromwärme-Verluste zu verursachen. TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/111 Institut für Elektrische Energiewandlung • FB 18 Anlasswiderstand im Ankerkreis zum Anfahren (2) Beispiel: Gleichstrommotor: UN = 430 V, PN = 200 kW, a = 92% (ohne Erregerverluste), Ra = 37.9 m Nennstrom: I N PN / a U N 506 A Anfahren ohne Anlasser: I a U N / Ra 430/ 0.0379 11350A 22.4 I N Strom ist viel zu hoch! Erforderlicher Anlass-Widerstand: Für Anfahren mit Nennstrom RAnlasser U N / I N Ra 430/ 506 0.0379 0.8 TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/112 Institut für Elektrische Energiewandlung • FB 18 Anlasswiderstand im Ankerkreis zum Anfahren (3) U I a Ra I a Ra Ra RAnlasser U n n n0 Ia k1 ( I f ) k1 k1 k1 Leerlaufdrehzahl n0 konstant Neigung von n(Ia) wird größer mit steigendem RAnlasser, (= Anfahren mit "Anlasser„) n n0 U = konst., = konst. Ra Ra + RAnlasser > Ra: Ia1 >> Ia2 bei n = 0 Ra + RAnlasser 0 0 Ia2 = U/(Ra + RAnlasser) TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/113 Ia1 = U/Ra Ia Institut für Elektrische Energiewandlung • FB 18 Gleichstrommotor am Batterienetz n n0 U = konst., = konst. Ra nL Me = Ms 0 0 • Auf welche Drehzahl läuft Motor hoch ? Ms Me1 ~ Ia1 Me Stationär gilt: Belastungsmoment Ms = Motormoment Me: dn/dt = 0 J d m M e M s 0 d m / dt 0 m konst. dt e d J : polares Trägheitsmoment von E-Maschine und Lastmaschine m Beispiel: Last heben: d Lastmoment ist UNabhängig von der Drehzahl: M s m g 2 Die Drehzahl steigt von n = 0 auf nL, wo Me = Ms ist. F m g Die Lastdrehzahl nL ist kleiner als die Leerlaufdrehzahl n0! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/114 Institut für Elektrische Energiewandlung • FB 18 Gleichstrommotor versus Asynchronmotor n n0 U = konst., = konst. nL Ia = Ms/(k2.) 0 0 Ms Me = Ms Me ~ Ia Me = Ms Fremderregter Gleichstrommotor Is Beispiel: Last heben d Ms F d / 2 Lastmoment unabhängig von der Drehzahl Asynchronmotor nL m F m g TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/115 Institut für Elektrische Energiewandlung • FB 18 Nebenschlussgenerator U f (I ) I I a I f ErzeugerZählpfeilsystem ! URem n = konst. Erregerwicklung E1-E2 parallel (= Nebenschluss) zum Anker A1-B2 geschaltet. U Rem k1 n Rem Arbeitspunkt A: entspricht der durch Selbsterregung eingestellten Ankerspannung bei Ia = 0 Wenn Stator-Eisenremanenz vorhanden: Angetriebener Generator liefert ohne jede Fremdspannungsquelle selbst Spannung. TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/116 Institut für Elektrische Energiewandlung • FB 18 Selbsterregung des Nebenschlussgenerators n = konst. URem U Rem k1 n Rem Stator-Eisenremanenzfluss Rem induziert im Leerlauf (Ia = 0) in der rotierenden Ankerwicklung die kleine “Remanenzspannung” URem URem treibt Feldstrom If = URem/(Ra + Rf + Rv), dessen Hauptfluss (If) den Remanenzfluss verstärkt Daher: Induzierte Spannung steigt an und treibt größeren Erregerstrom If = “Aufschaukeln” bis zum Spannungsgleichgewicht (Arbeitspunkt A) Erstpublikation: Werner von SIEMENS 1866 als Dynamoelektrisches Prinzip TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/117 Institut für Elektrische Energiewandlung • FB 18 Nebenschlussgenerator: „Selbstmordschaltung“ B: Falsche Selbsterregung: U < URem Erregerwicklung verkehrt angeschlossen = „Selbstmordschaltung“ A: Richtige Selbsterregung: U > URem em 0 em Hysterese-Schleife des Stator-Eisens Selbstmordschaltung: Bei vertauschten Klemmen E1, E2 erzeugt der Erregerstrom einen zum Remanenzfluss entgegen gesetzten Fluss und schwächt ihn: KEINE Auferregung ! Abhilfe: E1, E2 tauschen! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/118 Institut für Elektrische Energiewandlung • FB 18 Reihenschlussgenerator (Hauptschlussgenerator) Leerlaufspannung: bei Fremderregung messbar. Erzeuger-Zählpfeilsystem ! U 0 U i ( I f , I a 0) Innere Kennlinie: unkompensiert U i ( I f , I a 0) Serien(= Reihen)Schaltung von Anker und Erregung: Ia = If Belastungskennlinie: URem 0 0 n = konst. U U i I a Ra U b Remanenzspannung URem ist “Initialspannung”. Erst bei Belastung (= Stromentnahme Ia) steigen U und Hauptfeld an, weil der Belastungsstrom gleichzeitig Erregerstrom ist. Steigender Ia: Ankerspannungsfall IaRa steigt linear, induzierte Spannung Ui wegen Eisensättigung weniger als linear: Klemmenspannung U sinkt nach Maximum wieder ab. Bedeutung: Generatorische Bremse des RS-Motors (z. B. elektrische Bahn, Elektroauto). TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/119 Institut für Elektrische Energiewandlung • FB 18 Beispiel: Reihenschlussgenerator lädt Batterie Generator: Erzeuger-Zählpfeilsystem n = konst. Batterie: Verbraucher-Zählpfeilsystem U U i I a Ra U b U Batt U Batt ,0 I a RBatt ,i U b U i : U U i I a Ra Arbeitspunkt: stationär u( I a* ) U i I a* Ra U Batt ,0 I a* RBatt ,i u Batt ( I a* ) dynamisch: Generator di di udyn (t ) U i ia Ra La a u (ia ) La a u Batt (ia ) dt dt Dynamische Änderung des Ankerstroms ia auf Grund einer Störung ia0 des Arbeitspunkts Ia*: ia (t ) I a* ia (t ) u ( I a* ia ) u ( I a* ) La du ia dia u Batt ( I a* ia ) u Batt ( I a* ) dia dia du duBatt u (ia ) u Batt (ia ) La dt dt dia dia U Batt ( I a ) U (I a ) 1: INSTABILER 2: STABILER Arbeitspunkt 0 0 duBatt ia dia dia k ia k ia ia 0 ia (t 0) ia 0 dt La Arbeitspunkt 1: INSTABIL k du / dia duBatt / dia 0 Arbeitspunkt 2: STABIL k du / dia duBatt / dia 0 TECHNISCHE UNIVERSITÄT DARMSTADT U Batt ,0 Prof. A. Binder : Elektrische Maschinen und Antriebe 10/120 ia (t ) ia0 e( k / La )t Institut für Elektrische Energiewandlung • FB 18 Reihenschlussmotor (Hauptschlussmotor) Verbraucher-Zählpfeilsystem ! Erregerstrom = Ankerstrom: If = Ia Drehmoment: M e k2 ( I a ) I a Näherung: Sättigung = konstant: L´ = konst.: L I a Drehmoment steigt quadratisch mit Ankerstrom: U = konst. M e k2 L´I a2 Bei kleinen Ankerströmen (= kleiner Fluss ) gilt L´ = konst. exakt, da Eisensättigung erst bei größerem Fluss einsetzt! U U I a Ra Ra 1 U 1 Ra n(M)-Kennlinie: n 2k 2 2k 2 L I a 2 k 2 L M e 2k2 L Die Drehzahl des Reihenschlussmotors sinkt hyperbolisch mit der Belastung Me auf den Wert Null beim Anfahren. TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/121 Institut für Elektrische Energiewandlung • FB 18 Flusskennlinie und ihre Linearisierung L I a L I a I aN TECHNISCHE UNIVERSITÄT DARMSTADT I f Ia Prof. A. Binder : Elektrische Maschinen und Antriebe 10/122 Institut für Elektrische Energiewandlung • FB 18 Bedeutung des Reihenschlussmotors Reihenschluss-Motor darf nicht vollständig entlastet werden, da bei Ms = 0 der Motor auf sehr hohe Drehzahl beschleunigt (“Durchgehen”) und zerstört wird. Starke Drehzahlabnahme mit steigender Belastung = “weiche Kennlinie” Einsatzgebiete: Traktion (Eisenbahn: z. B. Italien 3 kV, DC-Netz), ältere Elektroautos a) Niedrige Drehzahlen (“Anfahren”): hohes Drehmoment = gute Beschleunigung b) Rad-Fahrweg-Kontakt (Rollwiderstand) und Luftwiderstand belasten den Antrieb stets. Beim Durchdrehen der Räder (“Schleudern”) bei nassem Fahrweg: Überdrehzahlschutz nötig! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/123 Institut für Elektrische Energiewandlung • FB 18 Drehzahlverstellung beim Reihenschlussmotor 1) Anfahren am Batterienetz: Anlasser! 2) Drehzahlverstellung durch Feldschwächung mit Shunt-Widerstand: Parallelwiderstand Rsh zur Feldwicklung (Shuntwiderstand): Verringerung des Stroms If durch die Feldwicklung = Flussverringerung = = Drehzahlanstieg I f R f I sh Rsh ( I a I f ) Rsh If Rsh 1 I a Rsh R f Ra 0 : „Scherung“: 0A 1 SA Verbraucher-Zählpfeilsystem ! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/124 Institut für Elektrische Energiewandlung • FB 18 Tandembetrieb auf einer Achse: Gleiche Drehzahl n Nebenschluss ungeregelt n Gleiches n Reihenschluss ungeregelt n Motor B Motor B Motor A Motor A Motor A und B leicht unterschiedlich angenommen! 0 0 M M M A B 0 0 M M M A B • Nebenschluss: Bei kleinen Unterschieden in der n(M)-Kurve große Unterschiede in der Motorbelastung: Motor B überbelastet! Schlechte Lastaufteilung ! Regelung nötig ! • Reihenschluss: Bei kleinen Unterschieden in der n(M)-Kurve kleine Unterschiede in der Motorbelastung: Motor B nicht überlastet! Gute Lastaufteilung ! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/125 Institut für Elektrische Energiewandlung • FB 18 Traktionsantrieb Drehgestell Radsatz A v B nRad,A nRad,B v d Rad , AnRad , A d Rad ,BnRad ,B v d RadnRad nRad , A nRad ,B d Rad ,B d Rad , A Drehzahl unterschiedlich auf unterschiedlichen Achsen A und B bei unterschiedlicher Radabnutzung ( = unterschiedliche Raddurchmesser)! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/126 Institut für Elektrische Energiewandlung • FB 18 Traktionsantrieb: Lastaufteilung bei gleicher Geschwindigkeit v Nebenschluss ungeregelt n Reihenschluss ungeregelt n nA nB nA nB Motor A Motor B 0 0 Motor A Motor B M M M A B 0 0 M M M A B • Motoren A, B seien identisch, aber auf unterschiedlichen Achsen. Unterschiedliche Radabnutzung: Bei gleicher Geschwindigkeit unterschiedliche Drehzahl nA und nB! • Nebenschluss: Motor B überbelastet! Schlechte Lastaufteilung ! Reihenschluss: Motor B nicht überlastet! Gute Lastaufteilung ! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/127 Institut für Elektrische Energiewandlung • FB 18 Prinzip der Wechselstrom-Kommutatormaschine • Erregerwicklung und Ankerwicklung in REIHE geschaltet (Reihenschluss-Motor) am Einphasen-Wechselstromnetz (Einphasen-Reihenschlussmotor). • Erregerstrom = Ankerstrom ia = Wechselstrom mit Frequenz f. Ankerstrom erregt Hauptfluss , daher pulsiert im Takt mit ia: und ia polen sich gleichzeitig um. • Drehmoment hat daher wegen M e ~ ia ( ) (ia ) stets dieselbe Richtung, pulsiert aber mit doppelter Frequenz 2f. TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/128 Institut für Elektrische Energiewandlung • FB 18 Pulsierendes Moment der Wechselstrom-Kommutatormaschine • Betrieb am Einphasen-Netz: Ankerstrom ist Wechselstrom mit Netzfrequenz. ia (t ) Iˆa sin( 2 f t ) • (t ) ˆ sin(2 f t ) Ankerwicklung und Feldwicklung in Serie geschaltet (Reihenschluss). Ankerstrom ist auch Erregerstrom für Fluss ~ ia. Beide wechseln gleichzeitig ihre Polarität mit f und erzeugen ein positives, aber mit 2f PULSIERENDES Moment (z. B.: f = 50 Hz, 2f = 100 Hz!). M e (t ) k2 (t )ia (t ) k2ˆ sin(2ft ) Iˆa sin(2ft ) M e (t ) k ˆ Iˆa (1 cos(2 2 f t )) / 2 M e (t ) k2 ˆ 2 I a,eff (1 cos(2 2 f t )) I a,eff Iˆa / 2 • NUR der Moment-Mittelwert Mav kann genutzt werden • Thermisch zulässige AC-Leistung ist nur 70% = 1/2 der DC-Leistung. M av k2ˆI a,eff / 2 - Gleiche Stromwärme: I a, DC I a,eff - Gleiche Eisensättigung: DC ˆ M DC / M av ( I a,DC ) /(ˆ I a,eff / 2 ) 2 TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/129 Institut für Elektrische Energiewandlung • FB 18 Transformatorische Funkenspannung kommutierende kommutierende vC „Funken“ Hauptfluss ist Wechselfluss (t ) ˆ sin(2 f t ) Wechselfluss induziert in kommutierende Spule transformatorische Funkenspannung: u (t ) N d (t ) / dt N 2 f ˆ cos(2 f t ) Tr c c Diese zündet zusätzliche „Funken“ an der ablaufenden Bürstenkante! Fazit: Wechselstrom-Kommutatormaschine hat mehr Bürstenfeuer als Gleichstrommaschine! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/130 Institut für Elektrische Energiewandlung • FB 18 Wechselstrom-Kommutatormotor-Kennlinie Einsatz mit Einphasen-Wechselstrom: DC-Betrieb: - Traktion bei 16.7 Hz: z. B. Deutsche Bahn: Statt 50 Hz ist f = 16.7 Hz zur Verringerung der transformatorischen Funkenspannung - Haushaltsgeräte bei 50 Hz: Universalmotor: Föhn, Bohrmaschine, Staubsauger: nmax = ca. 40000/min, ... n U I a Ra 1 U Ra 2k 2 2k 2 L I a AC-Betrieb: zusätzlich I a Ra I a ( Ra jLa f ) Drehzahlverstellung: DC: Verstellung der Ankerwechselspannung U a) Bahn: Stelltransformator mit Anzapfungen b) Haushaltsgeräte: Phasenanschnitt über TriacSchaltung! TECHNISCHE UNIVERSITÄT DARMSTADT AC: I a ,max Ua Ra2 (La f ) 2 Kleinmotor: Anfahren ohne Anlasser möglich! Prof. A. Binder : Elektrische Maschinen und Antriebe 10/131 Institut für Elektrische Energiewandlung • FB 18 Triac-Schaltung zur Ansteuerung kleiner Wechselstrom-Kommutatormaschinen 2 f Netz a) Zwei antiparallele Thyristoren (Steuerwinkel ) b) Alternativ: Ein Triac (= bidirektionaler Halbleiter-Schalter) versorgen mit der Ausgangsspannung u2 als Wechselspannung mit Phasenanschnitt. Durch die fehlende „Spannungs-Zeit-Fläche“ erhält der Motor im Mittel weniger Spannung: Deshalb sinkt seine Drehzahl. Nachteil: Wechselstrom ist nicht mehr sinusförmig, aber infolge der Glättung durch die Motorinduktivität „sinusförmiger“ als die Spannung u2. TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/132 Institut für Elektrische Energiewandlung • FB 18 Universalmotor • Kleiner, zweipoliger Motor für hohe Drehzahlen (typisch bis 40 000 /min), • Billigausführung für Massenproduktion • Keine Wendepole, daher Bürstenfeuer ABER: nur geringe Betriebsstundenzahl in Haushaltsgeräten • Betrieb am Haushalts-Einphasen-Netz 230V Ankerstrom ist Wechselstrom mit Netzfrequenz (z. B. f = 50 Hz). Quelle: R. Fischer, hanser-Verlag • Ankerwicklung und Feldwicklung in Serie geschaltet (Reihenschluss). • Ankerstrom ist auch Erregerstrom für den Fluss ~ ia. • Ankerstrom und Hauptfluss wechseln gleichzeitig ihre Polarität mit f (z. B. 50Hz) erzeugen positives, aber mit 2f (z. B. 2x50 = 100 Hz) PULSIERENDES Drehmoment TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/133 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe Zusammenfassung: Generator- und Motorschaltungen der Gleichstrommaschine - Gleichstrommaschine erlaubt Generator- und Motorbetrieb - Fremderregte Schaltung; Nebenschluss-Schaltung; Reihenschluss-Schaltung - Verbundschaltung (Kompoundschaltung) = Nebenschluss und Hilfs-Reihenschluss: Generatorbetrieb: Hilfs-RS kompensiert Spannungsabnahme –IaRa, so dass U(Ia) konst. für 0 Ia IN (siehe Skript) - Reihenschluss-Schaltung auch bei Wechselstrom einsetzbar (z. B. Universalmotor) TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/134 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe 10. Gleichstromantriebe 10.1 Die Funktionsweise der Gleichstrommaschine 10.2 Ankerwicklungen 10.3 Induzierte Spannung und elektromagnetisches Drehmoment 10.4 Ankerrückwirkung und Kompensationswicklung 10.5 Kommutierung des Ankerstroms und die Funktion der Wendepole 10.6 Generator- und Motorschaltungen der Gleichstrommaschine 10.7 Der drehzahlveränderbare Gleichstromantrieb 10.8 Leistungsgrenzen der Gleichstrommaschine TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/135 Institut für Elektrische Energiewandlung • FB 18 Drehzahlveränderbarer fremderregter Gleichstromantrieb U I a Ra I a Ra Ra U n n0 Ia k1 ( I f ) k1 k1 k1 Fremderregter Gleichstrommotor: Drehzahlveränderung durch a) Spannungsänderung U (U = Ua: Ankerspannung) b) Feldschwächung (über Uf: verminderte Erregerspannung) c) Widerstandserhöhung R + Ra (über Vorwiderstand R) TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/136 Institut für Elektrische Energiewandlung • FB 18 Fremderregter Gleichstrommotor: Drehzahlveränderung durch Spannungsänderung U n U I a Ra I R R U a a n0 a I a k1 ( I f ) k1 k1 k1 Leerlaufdrehzahl n0 geändert, n(Ia)-Kennlinie parallel verschoben n n01 n02 0 "Ankerstellbereich": 0 < n < nN entspricht 0 < U < Umax = UN bei = max = konst. U1 U2 < U1 Ia2= U2/Ra 0 n03 U3 < U2 TECHNISCHE UNIVERSITÄT DARMSTADT Ia1= U1/Ra Ia Negative Spannung U3: Drehzahlumkehr Prof. A. Binder : Elektrische Maschinen und Antriebe 10/137 Institut für Elektrische Energiewandlung • FB 18 Fremderregter Gleichstrommotor: Drehzahlveränderung durch Feldschwächung U I a Ra I a Ra Ra U n n0 Ia k1 ( I f ) k1 k1 k1 Leerlaufdrehzahl n0 geändert, Neigung von n(Ia) wird größer, wenn sinkt. n n02 n 2 < 1 1 U1 01 0 "Feldschwächbereich": nN < n < nmax entspricht max > > min bei U = Umax = UN = konst. Ia1= U1/Ra Ia 0 -1 U1 -n01 U1 TECHNISCHE UNIVERSITÄT DARMSTADT Negativer Fluss -1: Drehzahlumkehr Prof. A. Binder : Elektrische Maschinen und Antriebe 10/138 Institut für Elektrische Energiewandlung • FB 18 Fremderregter Gleichstrommotor: Drehzahlveränderung durch Widerstandserhöhung R + Ra n U I a Ra I R R R U a a n n0 a Ia k1 ( I f ) k1 k1 k1 Leerlaufdrehzahl n0 konstant, Neigung von n(Ia) wird größer mit steigendem R, z. B. Anfahren mit "Anlasser" (sonst nicht verwendet, da Verluste im Widerstand R) Ra1 = Ra + R1 n n0 Ra1 U 0 0 TECHNISCHE UNIVERSITÄT DARMSTADT U Ra2 = Ra + R2 R2 > R1 Ra2 > Ra1 Ia2= U/Ra2 Prof. A. Binder : Elektrische Maschinen und Antriebe 10/139 Ia1= U/Ra1 Ia Institut für Elektrische Energiewandlung • FB 18 Thyristor-Stromrichtergespeister Gleichstromantrieb Erzeugung einer variablen Ankerspannung aus dem Drehstromnetz L1, L2, L3 durch Gleichrichtung als Gleichspannung Ud für den Gleichstromantrieb Gesteuerter Drehstrom-Brücken-Gleichrichter B6C: Anker-Spannungsverlauf Schaltung für eine Stromrichtung Ia > 0 fNetz Für Stromumkehr Ia < Stromrichter nötig. 0 ist zweiter antiparalleler / t Ia 0 0 Veränderung der Ankerspannung über den Zündzeitpunkt (Zündwinkel ): "Zündwinkel" t , 2f Netz U d U d ,max cos , U d ,max U Netz 400V 2U Netz (3 / ) U d ,max 560V 0 : max. Spannung, 90 : Spannung ist Null, 180 : max. negative Spannung TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/140 Institut für Elektrische Energiewandlung • FB 18 (B6C)A(B6C)- Zwei antiparallele Thyristorbrücken Für Stromumkehr ist ein zweiter antiparalleler Stromrichter nötig. U d U 0, 0 Ia 0 U 0 Ia 0 U d U 0, 0 Ia 0 0 U 0 Ia 0 Ia 0 antiparalleler Stromrichter - Nachteil des Thyristor-Stromrichters B6C: Gleichspannung und -Strom haben Welligkeit mit 6-facher Netzfrequenz: z.B.: bei 50 Hz: 6 50 300Hz TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/141 Institut für Elektrische Energiewandlung • FB 18 Einquadranten-Transistor-Gleichstromsteller Gleichstromsteller (Chopper): Aus konstanter Gleichspannung (Batterie, Diodengleichrichter, ua U Batt ) wird durch Pulsweitenmodulation (PWM) eine gepulste Spannung ua mit veränderbarem Mittelwert Ud erzeugt Gepulste Ankerspannung ua ia,ss UBatt Welliger Ankerstrom ia UBatt Mittlere Gleichspannung Ud 0 0 Freilaufdiode erforderlich, da auf Grund der Zeitkonstanten Ta = La/Ra nach dem Abschalten des Transistors der Ankerstrom weiter fließen will. TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/142 Institut für Elektrische Energiewandlung • FB 18 Stromwelligkeit beim Transistor-Gleichstromsteller Mittlere Gleichspannung Ud ~ k: k Ud / U Batt Ton / T Hohe Transistorschaltfrequenz (z. B. fP = 2 kHz) kleine Stromwelligkeit ia,ss ! Stromwelligkeit maximal bei Aussteuergrad k = 0.5 Ra 0 : ia, ss U Batt (1 k ) k /( f P La ) ia , ss ia , ss,max UBatt Ud U Batt U Batt 4 f P La Ud 1.0 0 0 0 TECHNISCHE UNIVERSITÄT DARMSTADT 0.5 1.0 k 0 0.5 Prof. A. Binder : Elektrische Maschinen und Antriebe 10/143 1.0 k Institut für Elektrische Energiewandlung • FB 18 ia Vier-Quadranten-Transistor-Gleichstromsteller UBatt If > 0 UBatt 1 T2 ia > 0 ua > 0 ia < 0 ua < 0 Einquadranten-Steller: ia > 0, ua > 0 M > 0, n > 0 T3 T4 U d ua k1 n Vierquadranten-Steller: 2. Quadrant 1. Quadrant T1-T4: ia > 0, M k2 ia 3. Quadrant TECHNISCHE UNIVERSITÄT DARMSTADT 4. Quadrant T2-T3: ia < 0 ia > 0, ia < 0 ua > 0, ua < 0 M > 0, M < 0 n>0n<0 Prof. A. Binder : Elektrische Maschinen und Antriebe 10/144 Institut für Elektrische Energiewandlung • FB 18 WARD-LEONARD-Maschinensatz (-Umformer) Vorteile: keine Netzverzerrung keine Steuerblindleistung Tf = Lf/Rf n ~ U ~ I fG nASM Drehstrom-Asynchronmotor am Drehstromnetz (Drehzahl nASM) treibt Steuergenerator Steuergenerator fremderregt: Erregerstrom IfG z. B. aus Batterie Steuergenerator erzeugt über IfG variabel einstellbare Ankerspannung U U-gespeister GS-Motor kann drehzahlveränderbar betrieben werden: n ~ U ~ IfG Nachteile: a) drei Mal die Nenn-Maschinenleistung installiert (teuer!) b) drei Mal Verluste, z. B. Wirkungsgrad je Maschine 90 %: gesamt 0.93 = 0.73 = 73 %. c) geringe Dynamik: U-Änderung langsam, da Feldzeitkonstante Tf = Lf /Rf groß TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/145 Institut für Elektrische Energiewandlung • FB 18 Vierquadranten-Gleichstromantrieb Drehzahlumkehr durch (A) Umpolen der Ankerspannung von +U auf –U oder (B) Umpolen des Flusses auf -. (A) schneller als (B), da Anker-Zeitkonstante Ta = La/Ra deutlich kleiner als Feld-Zeitkonstante Tf = Lf/Rf . nmax 2 1 3 4 Betriebsgrenzen: maximale Drehzahl nmax, maximaler Ankerstrom Ia,max Ia,max -Ia,max -nmax Vierquadrantenbetrieb: (Verbraucher-Zählpfeilsystem) 2. Quadrant: n > 0, M < 0: U > 0, Ia < 0 GENERATOR 3. Quadrant: n < 0, M < 0: U < 0, Ia < 0 MOTOR TECHNISCHE UNIVERSITÄT DARMSTADT 1. Quadrant: n > 0, M > 0: U > 0, Ia > 0 MOTOR 4. Quadrant: n < 0, M > 0: U < 0, Ia > 0 GENERATOR Prof. A. Binder : Elektrische Maschinen und Antriebe 10/146 Institut für Elektrische Energiewandlung • FB 18 Vierquadranten-GS-Antrieb mit Feldschwächung 2 1. Quadrant 1 1 Ia,max = konst. 0 Mmax 0 Ia,max = konst. -Ia,max= konst. 3 Ia,max = konst. Vier Quadranten 4 Ankerstellbereich: Verändern der Ankerspannung Ua n(Ia)-Kennlinien parallel verschoben = Drehzahlveränderung (Fluss ist konstant). TECHNISCHE UNIVERSITÄT DARMSTADT Feldschwächbereich: Bei maximaler Ankerspannung UaN: weitere Drehzahlerhöhung durch Feldschwächung. Bei konstantem Ankerstrom sinkt das Drehmoment. Prof. A. Binder : Elektrische Maschinen und Antriebe 10/147 Institut für Elektrische Energiewandlung • FB 18 Vierquadranten-Gleichstrom-Betrieb Ankerstellbereich: Verändern der Ankerspannung U, Fluss = N = konst. U Ui I a Ra , Ui k1n0 N M e k2 N I a ~ I a n0 U /( k1 N ) n : n ~ U M max ~ I a,max (z.B. I a,max 2 I N ) Feldschwächbereich: Ankerspannung U = Umax = UaN = konst., Fluss verringert U U max konst.(z.B. : UaN ) n0 N UaN /( k1 N ) n0 / n0 N N / ~ 1 / n0 1 / n M max ( I a,max ) k2 I a,max ~ 1 / n TECHNISCHE UNIVERSITÄT DARMSTADT ~ 1/ n M max ~ 1 / n Prof. A. Binder : Elektrische Maschinen und Antriebe 10/148 Institut für Elektrische Energiewandlung • FB 18 Vier-Quadrantenbetrieb am Stromrichter ax • n(M)-Kennlinie: U M e Ra n k1 k1k2 2 • Weil über Stromrichter U = Ud variabel ist, wird Drehzahl über variables Ud verändert zwischen +Ud,max und -Ud,max. • Bei -Ud kehrt sich die Drehzahl um (Drehrichtungswechsel). • Drehzahl n0 = Ud,max/(k1) kann erhöht werden, wenn verringert wird (Feldschwächung). Es nimmt aber Mmax ab. M max k2 I a,max wenn ax TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/149 Institut für Elektrische Energiewandlung • FB 18 Stromrichtergespeiste FE Gleichstrommaschine vs. Umrichtergespeiste Asynchronmaschine Asynchronmaschine Gleichstrommaschine ax 0 0 • Ähnliche Kennlinienscharen bei Asynchron- und FE-Gleichstrommaschine. • Asynchronmaschine kann dynamischer als Gleichstrommaschine geregelt werden (ASM mit „feldorientierter Regelung“, ASM hat geringeres Trägheitsmoment) • Asynchronmaschine ist robuster, erlaubt: höhere Drehzahlen, höheren Wirkungsgrad, geringere Massen TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/150 Institut für Elektrische Energiewandlung • FB 18 Fremderregter Gleichstromantrieb: Grenzkennlinien (1) IN N PN UN MN Reaktanzspannungsgrenze Ankerstellbereich uR,max= 10 V Feldschwächbereich n < nN : n über Ankerspannung Ua ~ n erhöhen n > nN : Für n-Erhöhung muss Fluss ~ 1/n geschwächt werden. n > nR : Reaktanzspannung uR ~ Ia,max.n zu hoch = zu starkes „Bürstenfeuer" trotz Wendepole uR = 10 V begrenzt durch Ankerstromverringerung Ia,max ~ 1/n TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/151 Institut für Elektrische Energiewandlung • FB 18 Fremderregter Gleichstromantrieb: Grenzkennlinien (2) - Grenzkennlinien = Maximalwerte der Betriebsparameter z. B.: Mmax(n)-Grenzkennlinie = Einhüllende der M(n)-Kennlinienschar 1 : P U I a 2 n M Ankerstellbereich: max N M max k2 N I a,max ~ I a,max Pmax U I a,max ~ n I a,max ~ n Pmax 2 n M max ~ n Feldschwächbereich: ~ 1/ n Pmax M max ~ I a,max / n U max I a,max konst. Pmax 2 n M max ~ n (1 / n) konst. Reaktanzspannungsgrenze: I a ,max ~ 1 / n M max k2 I a,max ~ (1 / n) (1 / n) 1 / n2 TECHNISCHE UNIVERSITÄT DARMSTADT Pmax U max I a,max ~ 1 / n Pmax 2 n M max ~ n (1 / n2 ) ~ 1 / n Prof. A. Binder : Elektrische Maschinen und Antriebe 10/152 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe Zusammenfassung: Der drehzahlveränderbare Gleichstromantrieb - Fremderregter und Nebenschluss-erregter Gleichstrommotor - Drehzahlveränderung über Ankerspannung (Grunddrehzahlbereich) oder Hauptflussänderung (Feldschwächbereich) - Fluss-Schwächung für hohe Drehzahlen - Ankerspannung über Thyristor-Stromrichter oder Transistor-Chopper verändert - Ein- oder Vierquadrantenbetrieb - Prüffeld: WARD-LEONARD-Umformer fallweise im Einsatz TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/153 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe 10. Gleichstromantriebe 10.1 Die Funktionsweise der Gleichstrommaschine 10.2 Ankerwicklungen 10.3 Induzierte Spannung und elektromagnetisches Drehmoment 10.4 Ankerrückwirkung und Kompensationswicklung 10.5 Kommutierung des Ankerstroms und die Funktion der Wendepole 10.6 Generator- und Motorschaltungen der Gleichstrommaschine 10.7 Der drehzahlveränderbare Gleichstromantrieb 10.8 Leistungsgrenzen der Gleichstrommaschine TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/154 Institut für Elektrische Energiewandlung • FB 18 Kleinmotoren Einsatzbereiche der Kleinmotoren: Automobil 35,1% Haushalt Industrie 12,3% 11,5% Pumpen/Kompressoren 9,8% Heiz/Klimatechnik 9,7% Bürogeräte 5,9% Tragbare Werkzeuge 5,1% Medizintechnik 5,1% Sonstige 5,5% Quelle: Frost & Sullivan Gleichstrommaschinen dominieren im KleinmotorSektor (z. B. Automobilanwendung) oder als Universalmotor TECHNISCHE UNIVERSITÄT DARMSTADT Quelle: Faulhaber Permanenterregte zweipolige Gleichstrom-Kleinmotoren für Präzisionsantriebe der Feinwerktechnik Prof. A. Binder : Elektrische Maschinen und Antriebe 10/155 Institut für Elektrische Energiewandlung • FB 18 Leistungsgrenzen großer Gleichstrommaschine Die je Maschineneinheit baubare Leistung (“Einheitsleistung”) ist durch den Kommutator auf ca. 10 … 12 MW begrenzt. Quelle: Fa. Brenner, Bürstadt Grenzen: - Fliehkraftbegrenzung, sonst Deformation des Kommutators, Bürsten “hüpfen” starke Abnützung - Kommutierung: Reaktanzspannung uR < 10 V dauernd, < 20 V stoßweise, sonst starkes Bürstenfeuer trotz Wendepole, - Bürstenstromdichte: dauernd Jb < 12 A/cm2, < 20 A/cm2 stoßweise, sonst Ausglühen der Bürsten, - Segmentspannungsgrenze: im Mittel Us,av < 20 V, lokale Segmentspannung ohne Kompensationswicklung < 35 V, sonst Überschlag („Rundfeuer“)! Bei ungeregeltem Betrieb: Stabilitätsgrenze: fremderregter GS-Motor darf i. A. nur im Bereich der n(M)-Kennlinie mit negativer Steigung betrieben werden TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/156 Institut für Elektrische Energiewandlung • FB 18 Walzwerksantrieb: Stromrichtergespeister FE-Gleichstrommotor vs. Umrichtergespeister Vollpol-Synchronmotor Synchronmaschine Gleichstrommaschine Quelle: Siemens AG, Deutschland Nennleistung: 10.9 MW, 58.5 … 112.5/min Nennleistung: 12 MW • Synchronmaschine kann dynamischer als Gleichstrommaschine geregelt werden („feldorientierte Regelung“, geringeres Trägheitsmoment). • Synchronmaschine ist robuster: höhere Drehzahlen &Wirkungsgrad, geringere Massen, wartungsärmer. • Keine Tandembauweise bei Synchronmaschinen nötig, um hohes MN zu erreichen ! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/157 Institut für Elektrische Energiewandlung • FB 18 Gleichstrommaschinen - Ausblick Große Gleichstrommotoren werden durch a) stromrichtergespeiste Synchronmotoren (z. Zt. bis 100 MW) und b) Asynchronmotoren (z. Zt. bis ca. 40 MW) abgelöst. Auch im unteren Leistungsbereich Ablöse des stromrichtergespeisten Gleichstromantriebs durch den wartungsärmeren Käfigläuferasynchronmotor mit Umrichterspeisung und ggf. feldorientierter Regelung. Im Kleinmotorenbereich (Automobilanwendung) aber hohe Stückzahlen bei DC-Motoren 12 V / 24 V. TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/158 Institut für Elektrische Energiewandlung • FB 18 Elektrische Maschinen und Antriebe Zusammenfassung: Leistungsgrenzen der Gleichstrommaschine - Kommutator begrenzt Leistung pro Maschine wegen Spannung und Strom - Drehzahlbegrenzung durch Kommutator (Fliehkraft, Bürstenkontakt) - Leistungen je Maschine meist < 10 MW - Große Einsatzbereich der Gleichstrommaschine als Kleinmotor TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/159 Institut für Elektrische Energiewandlung • FB 18 Industrielle E-Antriebe – Überblick Festdrehzahlantrieb Drehzahlveränderbarer Antrieb Drehstrom Gleichstrom Netzspeisung Stromrichter Umrichter Umrichter KäfigläuferAsynchronmotor fremderregter Gleichstrom-M. KäfigläuferAsynchronm. PermanentmagnetSynchronmotor Ungeregelt einfache Kaskadenregel. feldorientierte Regelung feldorientierte Regelung Wirkungsgrad: gut mittel gut sehr gut Sehr robust Wartung robust robust Genormte Größen Motor: billig kein Umrichter TECHNISCHE UNIVERSITÄT DARMSTADT Drehstrom herstellerspezifische Ausführungen sehr teuer Umrichter: billig billig…teuer teurer teuer teurer groß kompakt sehr kompakt Prof. A. Binder : Elektrische Maschinen und Antriebe 10/160 Institut für Elektrische Energiewandlung • FB 18 That´s all, folks ! TECHNISCHE UNIVERSITÄT DARMSTADT Prof. A. Binder : Elektrische Maschinen und Antriebe 10/161 Institut für Elektrische Energiewandlung • FB 18