strecke α

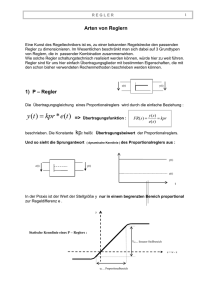
Steuer- und Regelungstechnik II, Übung PI-Regelkreis für eine P − T 1 -Strecke
KPR , T n
w
KPS , T 1
z
yR
e
1
y
x
−
GR (s)
GS (s)
a) Stellen Sie die Übertragungsfunktion des Regelstrecke auf.
b) Stellen Sie die Übertragungsfunktion des Reglers auf.
c) Stellen Sie die Übertragungsfunktion des Regelkreises für das Führungsgrößenverhalten
auf. Welche Ordnung hat das System?
d) Vereinfachen Sie die Übertragungsfunktion für den Sonderfall T n = T 1 . Welche Ordnung hat das System in diesem Fall?
e) Wie groß ist die Dämpfung D für T n , T 1 . Ansatz:
s2
1
α
mit D =
2
+ 2α · s + β
β
f) Bestimmen Sie für das Führungsgrößenverhalten die Regelabweichung für x(t → ∞)
für einen Eingangssprung. Wie groß ist die bleibende Regelabweichung?
Fortsetzung zur eigenen Übung.
g) Stellen Sie die Übertragungsfunktion des Regelkreises für das Störgrößenverhalten auf.
h) Wie groß ist die Dämpfung D für T n , T 1 . Ansatz:
1
α
mit
D
=
s2 + 2α · s + β2
β
i) Bestimmen Sie für das Störgrößenverhalten die Regelabweichung für x(t → ∞) für
einen Eingangsprung. Wie groß ist die bleibende Regelabweichung?
Steuer- und Regelungstechnik II, Übung PI-Regelkreis für eine P − T 1 -Strecke
a) Verhalten Regelstrecke: PT 1
GS (s) =
KPS
x(s)
=
y(s) 1 + sT 1
b) Verhalten Regler: PI
GR (s) =
yR (s)
1 + sT n
= KPR
e(s)
sT n
c) Führungsgrößenverhalten:
GR (s)GS (s)
x(s)
=
w(s) 1 + GR (s)GS (s)
KPR KPS (1 + sT n )
!
=
KPR KPS (1 + sT n )
(1 + sT 1 )(sT n ) 1 +
(1 + sT 1 )(sT n )
Gw (s) =
Gw (s) =
KPR KPS (1 + sT n )
(1 + sT 1 )(sT n ) + KPR KPS (1 + sT n )
Das System ist 2ter Ordnung.
d) Für T n = T 1
KPR KPS (1 + sT 1 )
(1 + sT 1 )(sT 1 + KPR KPS )
KPR KPS
Gw (s) =
sT 1 + KPR KPS
Gw (s) =
Das System ist nun 1. Ordnung.
e) D für T n , T 1
Gw (s) =
KPR KPS (1 + sT n )
(1 + sT 1 )(sT n ) + KPR KPS (1 + sT n )
Sortieren nach Potenzen von s:
=
KPR KPS (1 + sT n )
s2 T 1 T n + s(1 + KPR KPS )T n + KPR KPS
Isolieren der höchsten Potenz:
=
T1Tn
KPR KPS (1 + sT n )
!
(1 + KPR KPS ) KPR KPS
2
s +s
+
T1
T1Tn
2
Steuer- und Regelungstechnik II, Übung PI-Regelkreis für eine P − T 1 -Strecke
Bestimmen von α und β aus dem Ansatz:
(1 + KPR KPS )
mit α =
und β =
2T 1
r
KPR KPS
T1Tn
(1 + KPR KPS )
2T
D= r 1
KPR KPS
T1Tn
r
(1 + KPR KPS )
T1Tn
D=
2T 1
KPR KPS
r
(1 + KPR KPS )
Tn
D=
2
KPR KPS T 1
f) Sollwertsprung mit
w(t) = w0 · σ(t) w(s) =
w0
s
und
x(s) = w(s) · Gw (s)
Grenzwertbetrachtung (statischer Fall für t → ∞)
lim x(t) = lim s = ·x(s)
t→∞
s→0
daraus folgt:
x(∞) = lim s ·
s→0
w(0)
KPR KPS
Gw (s) = w0 ·
= w0
s
KPR KPS
Reglerabweichung:
e(∞) = w0 − x(∞) = 0
g) Störgrößenverhalten:
Gz (s) =
x(s)
KPS sT n
= 2
z(s) s T 1 T n + s(1 + KPR KPS )T n + KPR KPS
3
Steuer- und Regelungstechnik II, Übung PI-Regelkreis für eine P − T 1 -Strecke
Isolieren der höchsten Potenz:
Gz (s) =
T1
KPS s
!
(1
+
K
K
)
K
K
PR
PS
PR
PS
s2 + s
+
T1
T1Tn
h)
Bestimmen von α und β aus dem Ansatz:
Bestimmung von D =
α
β
(1 + KPR KPS )
mit α =
und β =
2T 1
(1 + KPR KPS )
D=
2
r
r
KPR KPS
T1Tn
Tn
KPR KPS T 1
i)
z(t) = z0 · σ(t) z(s) =
z0
s
und
x(s) = z(s) · Gz (s)
Grenzwertbetrachtung (statischer Fall für t → ∞)
lim x(t) = lim s · x(s)
t→∞
s→0
daraus folgt:
x(∞) = lim s ·
s→0
z(0)
Gz (s) = z0 ·
s
T1
KPS s
! =0
(1 + KPR KPS ) KPR KPS
2
s +s
+
T1
T1Tn
Ein s im Zähler verbleibt daher geht die die Auswirkung der Störung gegen 0.
4