gH g gH gA 125°

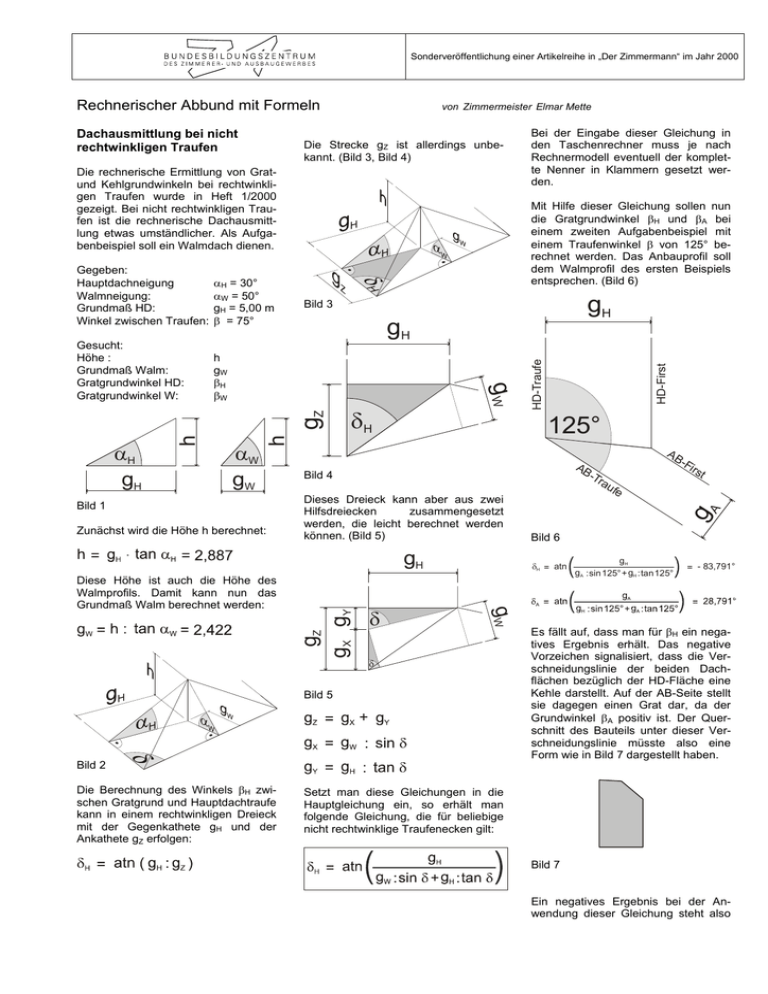
Sonderveröffentlichung einer Artikelreihe in „Der Zimmermann“ im Jahr 2000
Rechnerischer Abbund mit Formeln
Die Strecke gZ ist allerdings unbekannt. (Bild 3, Bild 4)
Die rechnerische Ermittlung von Gratund Kehlgrundwinkeln bei rechtwinkligen Traufen wurde in Heft 1/2000
gezeigt. Bei nicht rechtwinkligen Traufen ist die rechnerische Dachausmittlung etwas umständlicher. Als Aufgabenbeispiel soll ein Walmdach dienen.
h
gW
βH
βW
gH
Bild 1
Zunächst wird die Höhe h berechnet:
AB
-T
ra
u
Bild 4
Dieses Dreieck kann aber aus zwei
Hilfsdreiecken
zusammengesetzt
werden, die leicht berechnet werden
können. (Bild 5)
δ
δ
Bild 5
fe
Bild 6
δH
gW
Diese Höhe ist auch die Höhe des
Walmprofils. Damit kann nun das
Grundmaß Walm berechnet werden:
gZ
gX gY
gH
AB
-F
irs
t
gA
αW
gW
125°
h
h
αH
gH
δH
HD-First
Gesucht:
Höhe :
Grundmaß Walm:
Gratgrundwinkel HD:
Gratgrundwinkel W:
gH
Bild 3
gZ
αH = 30°
αW = 50°
gH = 5,00 m
β = 75°
Mit Hilfe dieser Gleichung sollen nun
die Gratgrundwinkel βH und βA bei
einem zweiten Aufgabenbeispiel mit
einem Traufenwinkel β von 125° berechnet werden. Das Anbauprofil soll
dem Walmprofil des ersten Beispiels
entsprechen. (Bild 6)
gW
Gegeben:
Hauptdachneigung
Walmneigung:
Grundmaß HD:
Winkel zwischen Traufen:
Bei der Eingabe dieser Gleichung in
den Taschenrechner muss je nach
Rechnermodell eventuell der komplette Nenner in Klammern gesetzt werden.
HD-Traufe
Dachausmittlung bei nicht
rechtwinkligen Traufen
von Zimmermeister Elmar Mette
atn
gH
gA : sin 125° + gH : tan 125°
- 83,791°
Es fällt auf, dass man für βH ein negatives Ergebnis erhält. Das negative
Vorzeichen signalisiert, dass die Verschneidungslinie der beiden Dachflächen bezüglich der HD-Fläche eine
Kehle darstellt. Auf der AB-Seite stellt
sie dagegen einen Grat dar, da der
Grundwinkel βA positiv ist. Der Querschnitt des Bauteils unter dieser Verschneidungslinie müsste also eine
Form wie in Bild 7 dargestellt haben.
Bild 2
Die Berechnung des Winkels βH zwischen Gratgrund und Hauptdachtraufe
kann in einem rechtwinkligen Dreieck
mit der Gegenkathete gH und der
Ankathete gZ erfolgen:
Setzt man diese Gleichungen in die
Hauptgleichung ein, so erhält man
folgende Gleichung, die für beliebige
nicht rechtwinklige Traufenecken gilt:
Bild 7
Ein negatives Ergebnis bei der Anwendung dieser Gleichung steht also
HD-First
HD-Traufe
gH
δH
δ
AB
-F
irs
t
fe
gA
AB A
-T
ra
u
Bild 8
δL
δR
140°
10
12
Die Gleichung lässt sich auch in anderen Bereichen einsetzen. So können
mit ihr beispielsweise die Gehrungswinkel von zwei ungleich hohen Treppenhandläufen oder zwei ungleich
hohen Stirnblenden, die nicht rechtwinklig zusammen treffen, berechnet
werden. (Bild 9)
Bild 9
In Bild 10 erhält man für den Winkel βL
ein negatives Ergebnis, d. h. er muss
auf der anderen Seite angetragen
werden.
δL δR
140°
Bild 10
8
immer für einen Kehlgrundwinkel.
Macht man sich klar, dass alle Kehlschifter vom First zur Kehle laufen, so
kann man sich leicht merken, dass der
Kehlgrundwinkel zwischen waagerechtem First und der Kehlgrundlinie
liegt. (Bild 8) Für weitergehende Berechnungen mit dem abgespeicherten
Kehlgrundwinkel muss dieser aber als
positiver Wert abgespeichert werden,
da es sonst zu Rechenfehlern kommen kann.
12
Sonderveröffentlichung einer Artikelreihe in „Der Zimmermann“ im Jahr 2000