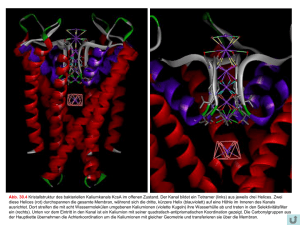
Das elektrochemische Ungleichgewicht der lebenden
Werbung

1 2 3 4 5 6 7 Einführung, Organisatorisches, Wurzeln der Biophysik Gimsa 9 10 4.4. 11.4. 16.4. 18.4. 23.4. 25.4. Datum 7.5. 9.5. 11 14.5. 12 16.5. Gimsa Gimsa Wachner Mol. Struktur biol. Syst. (MSBS): Elektrostatik, Atommodelle, Orbitale, Bindungen, chem. & elektr. Potentiale MSBS: molekulare & ionale Wechselwirkung, Wasserstruktur, Entropie, Molekülbewegung VL Grundlagen der Biophysik MSBS: Aktivierungsenergie, Debye-Hückel, Inter- & intramolekulare Wechselwirkungen Thermodynamik (TD): Grundlagen (Rekapitulation Physik &Chemie) Wachner TD: Elektrodeneigenschaften, Wasser- und Ionengleichgewicht, Osmotischer Druck Wachner TD: Donnan-Gleichgewicht, Nernst-Gleichung, Goldmann-Gleichung, Name Thema Gimsa Passive elektrische Eigenschaften (PEE): elektrische Zellstruktur, Oberflächenpotential, Elektrokinetik Baumann Membran als Grenzfläche: Grenzflächenspannung, Rastermikroskopietechniken Baumann Aktive elektrische Eigenschaften: Transmembranpotential, Nervenerregung, Patch-Clamp G8 Alternativveranstaltungen Seminar/Fragestunde und TESTAT 13 21.5. Gimsa 14 23.5. Gimsa 30.5. PEE: Feldverlauf um Zellen, Impedanz, induziertes Transmembranpotential PEE: elektrisch induzierte Kräfte, Elektrodeformation, Dielektrophorese, Elektrorotation Reserve (Pfingstwoche=Projektwoche) 15 4.6. Baumann 16 17 6.6. 11.6. Baumann Baumann BM: Skelett, Rheologie, Blutkreislauf BM: Strömungen, Schwimmen und Fliegen 18 13.6. Kuznetsov BM: Zytomechanik 19 18.6. Wachner Physikal. Umweltfaktoren: ionisierende Strahlung, Einführung in die Radioökologie 20 20.6. Haberland Physikal. Umweltfaktoren: nichtionisierende Strahlen 21 25.6. Sakowski Grundlagen der Systemtheorie: Kinetik, Stoffwechsel- und Austauschsysteme 22 27.6. Sakowski Grundlagen der Systemtheorie: Modelle zur Vermehrung, Populationskinetik 23 2.7. Biomechanik (BM): Ähnlichkeitsanalyse, Allometrie, Elastizität Pufferzeit bzw. Molekülstrukturaufklärung, Moleküldynamik (NMR/ESR) Baumann 24 4.7. 25 9.7. Seminar/Fragestunde 26 11.7. KLAUSUR Moderne Entwicklungen: biologische Anwendungen der Mikrosystemtechnik 1 Aktive elektrische 30.5.07, 20Uhr, Uni Rostock, 2 Ulmenstr. 69; Attac Diskussion http://www.g8-alternative-summit.org/de/ Transmembranpotential Eigenschaften Transmembranpotential Auftretende Potentiale Nervenerregung Wiederholung Diffusion/Flux/.. Patch Clamp Goldmann-Gleichung Nernst-Potential Diffusionspotential 3 Messung des Membranpotentials 4 Messung des Membranpotentials intrazelluläre Messung optisch (voltage sens. dyes) • Messung durch Einstechen einer Glasmikroelektrode dif Mo • Messung gegen Referenzelektrode über ein Voltmeter rom ft f dra ied I NM © Adam, Läuger, Stark: "Physikalische Chemie und Biophysik" 5 6 Nernst-Potential I Auftretende Potentiale (Membran nur für eine Ionensorte durchlässig) VMes sin tr . = (ϕ E1 − ϕ i ) + (ϕ i − ϕ a ) + (ϕ a − ϕ E 2 ) Diffusionspotential Elektrode 1 Membran -potential Diffusionspotential Elektrode 2 µ iel (1) = µ i0 + k BT ⋅ ln ci (1) + zi eψ (1) µ iel (2) = µ i0 + k BT ⋅ ln ci (2) + zi eψ ( 2) Bezeichnung Eigenschaften/Verwendung Nernstpotential Gleichgewichtspotential, wenn Membran nur für eine Ionensorte permeabel Goldmann-Gleichung Membran für mehrere Ionensorten permeabel Diffusionspotential Unterschiedliche Diffusionskoeffizienten der durch die Membran der Glasmesselektrode tretenden Ionen Donnanpotential Membran für einfache Ionen permeabel und für eine geladene Proteinsorte nicht permeabel Wiederholung für Fluxberechnung Membran Thermodynamische Berechnung c i (1) c i (2) ψ(1) ψ(2) µeli (2) = µiel (1) µ i0 + k BT ⋅ ln ci (1) + zi eψ (1) = µ i0 + k BT ⋅ ln ci (2) + zi eψ (2) zi e(ψ (2 ) −ψ (1)) = −k BT (ln ci (2 ) − ln ci (1)) k BT ci (2 ) ln zi e ci (1) RT ci (2 ) VM = ∆ψ = ψ (2 ) − ψ (1) = − ln zi F ci (1) kB = R / N L ∆ψ = ψ (2 ) −ψ (1) = − 7 F = e NL 8 Wiederholung für Fluxberechnung Was ist Diffusion? Brownsche Molekularbewegung unregelmäßige Teilchenverschiebung Materietransport Zufallsbewegung Konzentrationsunterschiede mit der Temperatur zunehmend Brownsche Molekularbewegung ungeordnete Wärmebewegung durch thermisch bedingte Zusammenstöße vom Botaniker Brown an Sporen entdeckt © Adam, Läuger, Stark: "Physikalische Chemie und Biophysik" 9 Wiederholung für Fluxberechnung 10 Wiederholung für Fluxberechnung 1. Ficksches Gesetz Elektrolytflux I Flux eines geladenen Teilchens (i) : r cw cw J i = − i i gradµ~i = − i i grad ( µi0 + RT ln ci + zi Fψ ) NL NL ⇒ Flux als Funktion des Konzentrationsgradienten ⇒ ungeladene Teilchen ⇒ stationäre Bedingungen, d.h. der Konzentrationsgradient ist räumlich und zeitlich konstant mit Diffusionskoeffizienten Di: r J i = − wi kTgradci = − Di gradci wi = Beweglichkeit [Di ] = m ci = Konzentration s Ji = − [J i ] = mol2 sm Di = Beweglichkeit kT ci wi d ( µ i0 + RT ln ci + zi Fψ ) N L dx bei isobarer sowie isothermen Bedingungen: Flux nur in Raumrichtung x: dc J i = − Di i dx wi = bei Flux nur in x-Richtung: 2 Ji = − 11 ci wi dµ~i cw =− i i N dx N RT dci dψ + zi F dx ci dx 12 Wiederholung für Fluxberechnung Nernst-Potential II Elektrolytflux II Bedingungen: als Spezialfall der Nernst-Planck-Gleichung c w dµ~i c w RT dci dψ Ji = − i i = − i i + zi F N dx N ci dx dx cI = konstant bis xI cII = konstant ab xII dc z Fc dψ J i = − Di i + i i RT dx dx ∆c/ ∆ x = konstant zwischen xI und xII mit Di = wi kT erhält man : Gleichgewicht => dc z Fc dψ J i = − Di i + i i RT dx dx z Fc dc z Fc dψ J i = 0 = − Di i + i i = dci + i i dψ RT dx RT dx Nernst-Planck-Gleichung ∆ψ = ψ I −ψ II = − Integration => RT ciI ln zi F c iII NernstPotential 13 14 Φ Goldman-Gleichung Herleitung innen ci z Fc dψ dc jυ = − Dυ υ + υ υ RT dx dx => Membran nur für eine Ionensorte (z.B. K) permeabel Nernst-PlankGleichung Vm Vm< 0 Analytische Lösung der Differentialgleichung mit folgenden Randbedingungen möglich: I K II K RT c ln F c Die elektrische Feldstärke in der Membran ist konstant z Fc dψ dc jυ = − Dυ υ + υ υ RT dx dx In der Realität: => Membran für mehrere Ionensorten permeabel c aK c aNa cCli ≠ ≠ c iK c iNa cCla GoldmanGleichung III Φ Herleitung innen ci Menbran aussen ca I = ∑ zυ jυ = 0 aussen ca Vm jK + jNa − jCl = 0 Vm ) ⋅ Dυ zυ eVm zυ e⋅Vm k B ⋅T ) Vm< 0 PK ⋅ x d ci ca mit : gυ = υ = υ cυ (0) cυ (d ) (Verteilungskoeffizient) zυ e⋅Vm z eV (ca − ci ⋅e k B ⋅T ) jυ = Pυ υ m υ υ zυ e⋅Vm kB T (1 − e k B ⋅T ) Vm< 0 0 0 k BTd ⋅ (1 − e Menbran 0 υ e ⋅V m k B ⋅T e⋅Vm k B ⋅T d e⋅Vm k B ⋅T eVm (c aK − c iK ⋅ e ) eV (c a − c iNa ⋅ e ) eV (c a − ciCl ⋅ e ) + PNa ⋅ m Na − PCl ⋅ m Cl =0 e ⋅V m e⋅Vm e ⋅Vm k BT kB T k BT k B ⋅T k B ⋅T (1 − e ) (1 − e ) (1 − e k B ⋅T ) Lösung der Differentialgleichung mit obigen Randbedingungen: gυ ⋅ (cυ − cυ ⋅ e innen ci ! ! ∂c z e ⋅V jυ = − Dυ υ − cυ ⋅ υ m ∂x k B ⋅T ⋅d jυ = 16 ortsunabhängigen Diffusionskoeffizienten und sie wandern unabhängig durch die Membran 0 zυ e⋅Vm k B ⋅T dψ V =E= m dx d • Membran wird als homogene Phase aufgefasst, d.h. jede Ionensorte hat einen 15 Differentialgleichung: i e = F / NL kB = R / NL ist die Innenkonzentration ebenfalls konstant Φ Goldman-Gleichung II a mit : ∂c z e ⋅Vm = − Dυ υ − cυ ⋅ υ k B ⋅ T ⋅ d ∂x • Membran ist in stationärem Zustand, d.h. bei konstanter Außenkonzentration => Goldman-Gleichung als Lösung der Nernst-Plank-Gleichung erforderlich Herleitung x d 0 (gute Näherung bei kleiner Ionenkonzentration in der Membran) => kein echtes Gleichgewicht mehr möglich weil aussen ca Menbran 0 Einfacher Fall beim Nernstpotential (Gleichgewichtszustand): ∆ψ = ψ I − ψ II = − Goldman-Gleichung I a i PK (cK − cK ⋅ e e⋅Vm k B ⋅T a a i ) + PNa (c Na − c Na ⋅ e a a e ⋅Vm k B ⋅T a i ) − PCl (cCl − cCl ⋅ e i i i e ⋅Vm k B ⋅T PK cK + PNa c Na − PCl cCl = (PK cK + PNa cNa − PClcCl ) ⋅ e )=0 e ⋅V m k B ⋅T Goldmann-Gleichung g ⋅D mit : Pυ ≡ υ υ d (Permeabilitätskoeffizient) 17 a a R ⋅ T PK cKa + PNa c Na + PCl cCli k B ⋅ T PK cKa + PNa c Na − PCl cCla = Vm = ln ln i i i i i a F e PK cK + PNa c Na + PCl cCl PK cK + PNa c Na − PCl cCl 18 x Ruhemembranpotential & Goldmann-Gleichung Vm = Vm = ∑ Pυ cυa + ∑ Pµ cµi R ⋅ T Kationen Anionen ln F i a ∑ Pυ cυ + ∑ Pµ cµ Anionen Kationen Auftretende Potentiale Verallgemeinerte Goldmann-Gleichung VMes sin tr . = (ϕ E1 − ϕ i ) + (ϕ i − ϕ a ) + (ϕ a − ϕ E 2 ) Diffusionspotential Elektrode 1 a R ⋅ T PK cKa + PNa cNa + PCl cCli ln i i a F PK cK + PNa cNa + PCl cCl Einfluss einer bestimmten Ionenart um so stärker, je a) größer das Konzentrationsgefälle b) höher die Permeabilität Membranpotential Membran -potential Vm = Diffusionspotential Elektrode 2 a R ⋅ T PK cKa + PNa cNa + PCl cCli ln i i a F P c P c + Na Na + PCl cCl K K Ruhezustand: PK : PNa : PCl = 1 : 0,04 : 0,45 19 Einleitung zum Diffusionspotential I mit : c+ ( x ) ≈ c− (x ) = c(x ) Flüsse beider Ionen schließlich gleich groß sowie : z+ = 1 und z− = −1 Auftreten in flüssiger Phase und Phasen, die von einer Membran getrennt sind Aus Grundbedingungen der Elektroneutralität zu berechnen dψ D − D− RT 1 dc =− + dx D+ + D− F c dx Integration über Membrandicke bzw. Kapillarlänge d VDiff = ψ (0) −ψ (d ) = D+ − D− RT c(d ) ln D+ + D− F c(0) 21 22 Welches Ion bestimmt das Membranpotenzial? Auftretende Potenziale Ion VMes sin tr . = (ϕ E1 − ϕ i ) + (ϕ i − ϕ a ) + (ϕ a − ϕ E 2 ) Membranpotenzial z Fc dψ z Fc dψ dc dc D+ + + + + = D− − + − − RT dx RT dx dx dx Einsetzen der Nernst-PlankFluxgleichungen Elektrisches Feld behindert Diffusion des „schnelleren“ Ions und beschleunigt das Gegenion © Adam, Läuger, Stark: "Physikalische Chemie und Biophysik" j + = j− Positiver und negativer Fluß ist gleich Aufgebaute Spannung = Diffusionspotential Diffusionspotenzial Elektrode 1 Diffusionspotentials II Berechnung des Elektrische Potentialdifferenz durch unterschiedliche Beweglichkeit der Ionen eines Salzes in einem Konzentrationsgradienten D+ > D− 20 Membran -potenzial Vm = Diffusionspotenzial VDiff = Diffusionspotenzial Elektrode 2 Konzen tration im Bl ut ca (m Mo l/l ) Ne rns t-P oten tial (m V ) V0 K+ 400 20 -75 Na + Cl - 50 440 +102 40 ....150 Vm = a R ⋅ T PK cKa + PNa cNa + PCl cCli ln i i a F P c P c + Na Na + PCl cCl K K D+ − D− RT cElektr. ln D+ + D− F cMedium Konzen tration im Axon ci (m Mo l/l ) 560 -68. ...-33 R ⋅T P c + P c + P c ln F P c +P c +P c a K K i K K a Na Na i Na Na i Cl Cl a Cl Cl Ruhezustand: PK : PNa : PCl = 1 : 0,04 : 0,45 Bei KCL ist D+ ≈ D− Bei Gliazellen entspricht Ruhepotenzial dem Kaliumpotential Bei Neuronen meist geringer (-55 bis – 65 mV) => geöffnete Natriumkanäle Für Gesamtbetrachtung zusätzlich Elektrodenpotenziale beachten! 23 24 Nervenerregung Neuronen auf Sensorchip Funktion Ionenkanal Verlauf Aktionspotenzial Auslösung des Aktionspotenzials Neuronen auf Elektroden DAB gefärbte Zellen auf Neurochip (nach 3 Tagen auf dem Chip) (nach 4 Wochen auf dem Chip) 25 26 (REM Bild vom EM Zentrum Universität Rostock) (DAB Bild von Simone Stüwe) Substanzspezifische Antwort Messung Aktionspotenziale Native Aktivität Blockade des GABAA Receptors Nur NMDA-Rezeptor modulierte Aktivität Parallele Messung an verschiedenen Elektroden auf dem Neurosensorchip. 27 28 Grundlage der Erregbarkeit Gewebespez. Dosis-Wirkungs-Kurve Lipiddoppelschicht undurchlässig für geladene Teilchen Ungleiche Verteilung von Ionen: Kalium, Natrium, Chlorid 100 Verteilung durch Transporter aufrechterhalten Rückenmark Auditory Cortex 90 80 Mit ATPase pro ATP 3 Na+ nach außen und 2 K+ nach innen 70 Aufbau von Konzentrationsgradienten 60 50 40 30 Ion 20 10 0 0.1 1 10 Konzen tration im Axon ci (m Mo l/l ) Konzen tration im Bl ut ca (m Mo l/l ) Ne rns t-P oten tial V0 (m V ) 100 TMTC Konzentration [µM] 29 K+ 400 20 -75 Na + Cl - 50 440 +102 40 ....150 560 -68. ...-33 30 Die Natrium-Kalium ATPase Funktionsweise eines Ionenkanals pro ATP 3 Na+ nach außen und 2 K+ nach innen Membranintegrale Proteine als hydrophile Pore: o selektiv für Ionen o i. d. R. regulierbar Bindungsstellen und Energiemaxima für spezifisches Ion o Bindungsstellen erleichtern den Durchtritt o Energiemaxima oszillieren beim Durchtritt des Ions In Nervenzellen muss Na+ von einer Konzentration von 143mM auf 14mM (im Zytosol) und K+ von 4 auf 157mM gebracht werden. © Dudel, Menzel, Schmidt: "Neurowissenschaften" 31 Aufbau Ionenkanal 32 Modell eines Natriumkanals Spannungsabhängige Kanäle mit ähnlicher Struktur o gleicher genetischer Ursprung Ionenkanäle aus mehreren Domänen: o 4 hydrophobe Domänen verankern den Kanal in der Membran o 4 hydrophile Sequenzen bilden hydrophile Pore (H5) o Sequenz A4 in der hydrophoben Domäne besitzt ATP-Bindungsstelle o Intrazelluläre Domänen Kaliumkanal aus vier identischen Untereinheiten © Dudel, Menzel, Schmidt: "Neurowissenschaften" 33 34 Wie kommt die Ionenselektivität zustande? Struktur der K-Kanals Chloridionen durch Ladung selektiert: o Pore mit positiven Bindungsstellen Kalium im hydratisierten Zustand klein o Durchtritt nur mit Hydrathülle Natrium im unhydratisierten Zustand klein o Trennung von der Hydrathülle beim Durchgang © Kandel, Jessell, Schwartz. "Principles of neuroscience" 35 36 Was ist ein Aktionspotenzial? Verlauf des Aktionspotenzials Informationsvermittelndes Signal Zusammenbruch des Ruhepotenzials bis zu positiven Werten von ca. +40 mV => Depolarisierung; in ca. 500 µs Depolarisierung bis zum Schwellenpotenzial Beim Schwellenpotenzial Öffnung spannungsabhängiger Na+-Kanäle Natriumeinstrom => Depolarisierung Rückkehr zum Ruhepotenzial mit Hyperpolarisierung => Repolarisierung, in ca. 500 µs Deaktivierung der Natriumkanäle beendet Einstrom Alles-oder-Nichts-Vorgang Depolarisierung verstärkt Kaliumausstrom => Repolarisierung absolute Refraktärzeit von 2 ms (keine Erregbarkeit) Inaktivierung des Natriumkanals => Refraktärzeit 37 38 Aktionspotenzial Auslösung Ströme beim Aktionspotenzial Aktionspotenzial von spannungsabhängigen Natriumkanälen getragen Aktionspotenzial mit verschiedenen Stromkomponenten Natriumeinstrom und Kaliumausstrom Anstieg zum Schwellenpotenzial aus verschiedenen Gründen: o Potenzialänderung durch präsynaptische Zelle bei elektrischen Synapsen Isolierung der Ströme durch selektive Blockade o Rezeptorpotenziale bei Sinneszellen o Natrium => Tetrodoxin, TTX o Neurotransmitterbindung an ligandengesteuerten Ionenkanälen o Kalium => Triethylamin, TEA Nachweis der Spannungsabhängigkeit o Second-messenger-Bindung z. B. Ca2+, cAMP, DAG Beschreibung mit Kanalleitfähigkeiten (Hogdgin-Huxley) © Kandel, Jessell, Schwartz. "Principles of neuroscience" Depolarisierung zum Schwellenpotenzial immer durch Natrium- oder Calciumeinstrom 39 Kanäle können unterschiedlich getriggert werden 40 Aktionspotenzial Ausbreitung Ausbreitung der Aktionpotenziale über lange Strecken an Axonen Passive Ausbreitung läßt Signal an Widerständen versiegen Aktionspotenzial treibt benachbarte Membran über das Schwellenpotenzial Aktive Fortleitung durch fortgesetzte Auslösung => „Zündschnureffekt“ Inaktivierung der Natriumkanäle verhindert Zurücklaufen des Aktionspotenzials © Dudel, Menzel, Schmidt: "Neurowissenschaften" 41 42 Nervenzellen Signalleitung Signal direction Ausbreitung des Aktionspotentials Dendrites AP-Ausbreitungsgeschwindigkeiten in Nervenfasern (aus C.L.Schauf et al.) Cell body Cell body Nerv Durchmesser Myelin v Riesenaxon 500µm nein 25m/s großer motorischer Nerv, Beinmuskel 20µm ja 120m/s Nerven von Druckrezeptoren der Haut 10µm ja 50m/s Nerven von Schmerzrezeptoren 1µm nein 2m/s Node of Ranvier Myelin sheath Signal pathway Axon Schwann cell Nucleus Nucleus Nodes of Ranvier Myelin sheath Schwann cell Synaptic knobs Copyright © 2003 Pearson Education, Inc. publishing as Benjamin Cummings 43 44 Prinzip der Patch-Clamp-Technik von Neher und Sakmann Ende der 70er erfunden (Nobelpreis 1991) Zelle wird mit Glaselektrode angesaugt => Gigaseal, d. h. mit > 1 GΩ PatchClampTechnik Danach entweder Herausreißen der Membran oder Öffnen der Membran unter der Elektrode Im Membranfleck optimal nur ein Ionenkanal von jeder Sorte => Einzelkanalaufnahmen Prinzip der Patch-Clamp-Technik Bei Öffnen der Membran: Whole-Cell-Aufnahmen Patch-Clamp Mess-Modi Beispiele Patch-on-Chip Systeme © Kandel, Jessell, Schwartz. "Principles of neuroscience" 45 Messapparatur von Neher/Sakmann 46 Messung I Deutsches Museum Bonn 47 Universität Karlsruhe 48 Mess-Schaltung Messaufbau Operationsverstärker 49 Patch-Clamp Mess-Modi Charite, Berlin 50 Einzelkanal-Aufnahmen Whole-Cell: Im inside-out oder outside-out Modus Membrandurchbruch in Pipettenöffnung; Summe vieler Ionenkanäle Einzelne Kanalöffnungen messbar Gequantelter Charakter der Kanalöffnungen sichtbar On-Cell: Ströme zeigen immer die volle Amplitude Einsaugen Zellmembranfleck ohne die Zelle zu zerstören; Einzelkanalmessungen Kanäle können nur ganz geöffnet oder geschlossen sein o z. B. Kaliumstrom im Inside-out-Modus o kleine Amplitude ≈ 2 pA Excised (inside-out): Zellmembraninnenseite weist nach außen; komplizierte Herstellung, Einzelkanalmessungen © Numberger, Darguhn: "Patch-Clamp-Technik" 51 Whole-Cell-Aufnahmen 52 Ersatzschaltbild der Zelle im Patch-Clamp Summe aller Öffnungen eines Kanaltypen können gemessen werden Zellwiderstand R ≈ 1 GΩ Gesamtstrom über der Zellmembran Zellkapazität C ≈ 1-10 pF große Amplituden ≈ 800 pA Pipettenwiderstand RS ≈ 10 MΩ („rohe“ Elektroden mit 2 - 5 MΩ => Zellkomponenten erhöhen Widerstand) ER: Haltepotential VP: Pipettenpotential (VP wird vom Verstärker angelegt bzw. gemessen, dabei muss RS überwunden werden) © Numberger, Darguhn: "Patch-Clamp-Technik" © Numberger, Darguhn: "Patch-Clamp-Technik" 53 © Neher, Sakmann: "Single-channel-recording" 54 Funktion Spannungsklemme (Voltage-Clamp) Current-Clamp-Technik Umkehrung der Spannungsklemme von Cole und Curtis in den 30er Jahren entwickelt Strom wird vorgegeben und resultierende Spannung gemessen. Prinzip: Spannung konstant => Messung des Kompensationsstroms Gleicher Schaltkreis wie bei Voltage-Clamp mit zusätzlicher Rückkopplung Es wird ein Kompensationsstrom erzeugt, der genauso groß ist wie der Strom der durch die Membran fließt 55 Patch-on-Chip Systeme 56 Realisierungsbeispiel AVIVA 57 Realisierungsbeispiel Cytocentrics 58 Patch-on-Chip Gesamtsystem © Taylor & Francis 59 Cytocentrics AG, Rostock 60 Literatur Einsatzgebiete Adam – Läuger – Stark (2003), Physikalische Chemie und Biophysik , Springer Verlag Erwin Neher und Bert Sakmann, Die Erforschung von Zellsignalen mit der Patch-Clamp Technik, Spektrum der Wissenschaft (Mai 1992) Vorteile Patch-on-Chip Systeme: geringer apparativer Aufwand (Platz, Kosten, ..) NMI Natural and Medical Sciences Institute at University of Tuebingen, Germany Bedienung auch durch ungeübtes Personal www.uni.kiel.de/zbm/forschung/patch.html leichte Parallelisierbarkeit => hoher Durchsatz an Messungen www.charite.de/gastroenterologie/Forschung/patbeisp.de www.biologie.de/biowiki/Patch-Clamp-Technik Einsatzgebiete: Biomedizinische Forschung www. www. Itb.uni Itb.uni--karlsruhe.de karlsruhe.de Medikamentenentwicklung 61 62