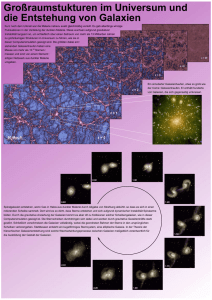
3. Optische Durchmusterungen
Werbung

3. Optische Durchmusterungen Bereich: ~ 0.3 - 2 m = 300 – 20000 Å = 1 • 1016 - 1.5 • 10 14 Hz 0.3-1 m : Optischer Bereich, < 0.3 m Atmosphäre undurchlässig, > 1 m limitierung CCDs; 1-2 m nah-Infrarot Bereich, NIR-Kameras Filtersysteme Filter central (Å) FWHM (Å) Fluss (0 mag) Fluss (20 mag) Jy mJy Johnson U 3650 525 1880 0.0188 Johnson B 4450 1010 4440 0.0444 Johnson V 5500 830 3810 0.0381 Johnson R 6930 2100 3010 0.0301 Johnson I 8790 1705 2430 0.0243 Cousins R 6590 1570 3080 0.0308 Cousins I 8060 1540 2550 0.0255 J 12000 1500 1770 0.0177 H 16000 1500 1110 0.0111 K 22000 2000 630 0.0063 Die Hubble-Sequenz Morphologische Klasssifikation der normalen Galaxien Elliptische Galaxien Galaxien mit elliptischen Isophoten, nahezu strukturlos. Einteilung nach Elliptizität: e = 1 – b/a , a,b = große, kleine Halbachse Notation: En, n = 10e, 0 < e < 0.7, E4 hat b/a = 0.6, E0 = kreisförm. 1. Normale Ellipsen: MR = - 23 bis –15 2. cD-Galaxien: extrem helle (MR bis – 25) und große Ellipsen (M87) 3. Kleine Ellipsen: dwarf ellipticals (dE), kleinere Flächenhelligkeit, niedrigere Metallizität (Metalle: Elemente schwerer als Helium) + dwarf Spheroidals (dSph), sehr leuchtschwach (MR bis - 8), nur in lokaler Gruppe zu finden 4. Blaue kompakte Zwerggalaxien: Blue compact dwarfs (BCD), enthalten im Gegensatz zu anderen Ellipsen viel Gas und Staub, zeigen teilweise starke Sternentstehung Morphologie Die Isophoten (Linien gleicher Helligkeit) von elliptischen Galaxien zeigen Abweichungen von reinen Ellipsen. Kann in Fourier-Reihe zerlegt werden: R( ) = a0+ a2• cos(2 ) + a4 • cos(4 ) + ... a4 > 0: Isophote erscheint scheiben/zitronenförmig a4 < 0: Isophote erscheint kastenförmig disky boxy Disky E‘s sind schwache Radio- und Röntgenstrahler Boxy E‘s haben breite Verteilung von Radio-/Röntgenstrahlung (sehr oft von aktiven Kernen) • ca. 90% aller Ellipsen sind disky • Boxy E‘s zeigen oft Anzeichen von Verschmelzung (merger) in Vergangenheit ‘alte (UL)IRGS?‘ . Boxy E‘s: Massereichste Ellipsen (bis 1013 M ), bis 100 kpc Radien Sterne zeigen (fast) keine geordnete Bewegung: Linienverbreiterung aus statistischer Bewegung der Sterne im Potential Geschwindigkeitsdispersion: einige 100 km/s Disky E‘s: weniger massereich, weniger groß, enthalten oft stellare Scheibe Sterne zeigen z.T. geordnete Bewegung (rotationsabgeplattet) in der Größenordnung ihrer statistischen Bewegung Elliptische Galaxien werden als dynamisch heiße Systeme bezeichnet Erweiterung - S0-Galaxien (lenticulars): Übergang zu den Spiralgalaxien. Enthalten zusätzlich ausgeprägte Scheibe, aber keine Spiralarme! Elliptische Galaxien und S0-Galaxien werden rein historisch auch als Frühtyp-Galaxien (early-type) bezeichnet: . Spiralgalaxien Kombination aus Scheibe mit Spiralarmen und zentraler Verdickung (Bulge). Die Bulges sind dynamisch denen von disky E‘s sehr ähnlich. Unterteilung in normale Spiralen (S) und Balkenspiralen (SB). Sequenz a – c (Sa, Sb bzw. SBa, SBb etc.) entprechend dem Verhältnis Bulge zu Scheibe. WICHTIG: keine Aussage über Entwicklungszustand!!! Lbulge/Ldisk ~ 0.3 für Sa, ~ 0.05 für Sc Öffnungswinkel der Spiralarme: ~ 6o für Sa, ~ 18o für Sc Helligkeitsverteilung in den Spiralarmen nimmt von Sa zu Sc zu. In Sa nahezu glatt, in Sc helle Klumpen von HII-Regionen (Sternentstehung) Kleinerer Helligkeits- und Massenbereich als elliptische Galaxien MR = -16 bis –22, 109 – 1012 M Sterne und Gas in Scheibe zeigen im Gegensatz zum Bulge geordnete Rotation (dynamisch kalt). Rotation steigt zum sichtbaren Außenbereich hin stärker an als aufgrund des Keplergesetzes erwartet Dunkler Halo (Dark Matter) Natur unklar!!! Form der Rotationskurve ist nahezu unabhängig von Hubble-Typ 90% der Masse liegt in Form der Dunklen Materie vor Tully-Fisher Relation (Tully & Fisher 1977): Rotationsgeschwindigkeit streng korreliert mit Leuchtkraft −4 L ∝ ν max D.h. Leuchtkraft kann genau bestimmt werden. Da Korrelation sehr streng, dann die Tully-Fisher Relation auch direkt zur Entfernungsbestimmung verwendet werden !!! Helligkeitsprofil Die radiale Helligkeitsverteilung von Galaxien kann durch ein verallgemeinertes Helligkeitsprofil beschrieben werden: I (r ) = I (re ) ⋅ dex − bβ : Formparameter r re β −1 = 1/n, n = 1..10 re: Halblichtradius (Radius, der 50% des Lichtes umfasst) b : -abhängiger Parameter N = 1: Exponentielles Profil Scheibe N = 4: de Vaucouleurs Profil; I ∝ r-1/4 elliptische Galaxien/Bulges Oberflächenhelligkeit einer elliptischen Galaxie aufgetragen gegen r1/4 Oberflächenhelligkeit von Spiralgalaxien. Bei NGC 4459 ist Kombination von Bulge und Scheibe gut zu sehen Irreguläre Galaxien Galaxien mit wenig oder keiner Struktur (Irr I, Irr II). Spiralsequenz später erweitert um Klassen Sdm, Sm, Im und Ir m = Magellansch, Große Magellansche Wolke (LMC) ist SBm Charakteristisch: sehr starke Sternentstehung, meiste Galaxien bei hohen Rotverschiebungen sind irregulär Spektrale Eigenschaften Allgemein: Je später der Galaxientyp, desto blauer die Farbe, d.h. E‘s sind relativ rot (U-B = 1) + dominiert durch alte, kühle Sterne, Sc‘s und später sind sehr blau (U-B < 0), starke Sternenstehung. Galaxienspektren: Summe der Einzelspektren aller Sterne, bestehend aus dem Kontinuum (genereller Verlauf der Flussabgabe) überlagert von Absorptions- bzw. Emissionslinien. Die Linien können entweder aus den Sternen selbst stammen oder interstellaren Ursprungs sein. Erlaubte Linien Rekombinationsstrahlung, freies Elektron wird von Ion eingefangen und kaskadiert in den Grundzustand: z.B. H , H Verbotene Linien Stoßanregung in Gebieten geringer Dichte. Thermische Elektronen regen Zustände geringer Übergangswahrscheinlichkeit an. Da Dichte jedoch sehr gering erfolgt keine Stoßabregung, sondern Emission von Photonen: z.B. [O II], [O III] Galaxienspektrum Ellipse Na D Mg-Band G-band 4000 Å Charakteristische Absorptions-Features in elliptischen Galaxien von kühlen Sternen (i.w. K-Riesen mit 3500-4000 K Oberflächentemperatur. Speziell 4000 Å Break ist wichtiges Kriterium für photometr. Rotversch. Galaxienspektrum Sb Galaxie G-band Mg-Band Na D H [S II] 4000 Å 4000 Å Break + andere Absorptionsfeatures vom Bulge nicht so stark ausgeprägt. Emissionslinien aus Nebelgebieten mit Sternentstehung Galaxienspektrum Irreguläre Galaxie [O II] 4000 Å H [O III] H [S II] 4000 Å Break sehr schwach. Spektrum dominiert durch Emissionslinien aus Sternentstehungsgebieten. Deutlich ist auch das blauere Spektrum im Vergleich zur elliptischen Galaxie zu erkennen. Spektrale Verteilung - Überblick Wichtigste Linien in Galaxienspektren Ly-Lim 912 Si IV 1394 C III] 1909 [Ne III] 3869 [O III] 5007 [N II] 6584 Ly 973 Si IV 1403 C II] 2326 Ca K 3933 Mg b 5174 [Si II] 6717 Ly 1026 Si II 1527 Fe II 2344 Ca H 3969 [N I] 5199 [Si II] 6731 C III 1175 C IV 1548 Fe II 2374 4000 Å 4000 E-Band 5269 Ca II 8498 Ly 1216 C IV 1551 Fe II 2587 H 4101 He I 5876 Ca II 8542 NV 1239 Fe II 1608 Fe II 2600 Ca I 4226 Na D 5893 Ca II 8662 NV 1243 Fe II 1640 Mg II 2795 g-Band 4304 [O I] 6300 Si II 1263 Al II 1670 Mg II 2803 H 4340 Ba I 6497 O I/Si II 1303 AL III 1855 H-Lim 3648 H 4861 [N II] 6548 C II 1335 Al III 1863 [O II] 3727 [O III] 4959 H 6563 • Wichtigste Emissionslinien; • Wichtigste Absorptionslinien Abs./Emissionslinien im optischen nur bis z ~ 1.3 hilfreich (danach im nah-Infraroten), für z > 2 ist vor allem Ly wichtig Der Nachthimmel Warum optische Durchmusterungen? a) Morphologie der Galaxien ändert sich stark als Funktion von z ! b) Sternbildungsrate nimmt von z = 1 bis heute um einen Faktor 10 ab, ist zwischen z = 1-3 in etwa konstant + bei größerem z ? c) Modelle der hierarchischen Strukturbildung sagen Bildung von kleinen Fragmenten voraus, die später zu großen Galaxien anwachsen (größtenteils innerhalb Haufen d) Wie funktioniert chem. Anreicherung (Metalle), bei großem z nur heiße, kurzlebige Sterne? Verständnis dieser Prozesse/Fragestellungen nur möglich über Durchmusterungen Charakterisierung der Galaxienpopulation als Fkt. von z generell Follow-up Untersuchungen von Einzelfällen . Warum optische Durchmusterungen? a) Morphologie der Galaxien ändert sich stark als Funktion von z ! b) Sternbildungsrate nimmt von z = 1 bis heute um einen Faktor 10 ab, ist zwischen z = 1-3 in etwa konstant + bei größerem z ? c) Modelle der hierarchischen Strukturbildung sagen Bildung von kleinen Fragmenten voraus, die später zu großen Galaxien anwachsen (größtenteils innerhalb Haufen d) Wie funktioniert chem. Anreicherung (Metalle), bei großem z nur heiße, kurzlebige Sterne? Verständnis dieser Prozesse/Fragestellungen nur möglich über Durchmusterungen Charakterisierung der Galaxienpopulation als Fkt. von z generell Follow-up Untersuchungen von Einzelfällen Butcher – Oemler Effekt (1984): Anzahl der blauen Galaxien in Galaxienhaufen steigt mit z stark an! Sternbildungsrate als Funktion von z Hippelein, 2003 Warum optische Durchmusterungen? a) Morphologie der Galaxien ändert sich stark als Funktion von z ! b) Sternbildungsrate nimmt von z = 1 bis heute um einen Faktor 10 ab, ist zwischen z = 1-3 in etwa konstant + bei größerem z ? c) Modelle der hierarchischen Strukturbildung sagen Bildung von kleinen Fragmenten voraus, die später zu großen Galaxien anwachsen (größtenteils innerhalb Haufen) d) Wie funktioniert chem. Anreicherung (Metalle), bei großem z nur heiße, kurzlebige Sterne? Verständnis dieser Prozesse/Fragestellungen nur möglich über Durchmusterungen Charakterisierung der Galaxienpopulation als Fkt. von z generell Follow-up Untersuchungen von Einzelfällen Technische Einschränkungen z = 0: Meiste diagnostische Linien im optischen Wellenlängenbereich Detektoren (CCDs) im optischen am empfindlichsten + größten Problem: Für höhere Rotverschiebungen wandern optische Linien ins nah-Infrarot: z= λ ( Beobachtet ) − λ ( Labor ) λ ( Labor ) Beispiel: z = 1.5 λ ( Beobachtet ) = λ ( Labor ) • (1 + z ) [O III] (3727 Å) 9318 Å !!! d.h. ab z ~ 1.5 wandern alle optischen Linien in das nah-Infrarot! Problem hier: nah-Infrarot Detektoren weniger empfindlich und klein Erst ab z = 2 Ly (1215 Å) 3645 Å d.h. erst für z > 2 wieder eine starke Linie im optischen Bereich Bereich z = 1.5-2 sehr schwierig, Kontinuumsverlauf muss gemessen werden Weiteres Problem hier: Objekte bei diesem z schwach (23-25 mag), Spektroskopie nur mit 8-10m Teleskopen möglich Zeitintensiv: ca. 10h Belichtungszeit Multiobjektspektroskopie: nur einige 10 Objekte pro Feld beobachtbar sehr zeitaufwendig Lösung: Schätzung von z und Galaxientyp aus photometrischen z Vorteil: Viele Objekte gleichzeitig !!! Beispiel: QSOs aus dem Sloan Digital Sky Survey Konzept der photometrischen Rotverschiebungen Prinzip: Kombination von mehreren Filtern, ‘‘Spektrum‘‘ einer Galaxie mit sehr niedriger Auflösung (100-500 Å gegenüber 10 Å mit klassischen Spektrographen) 1) Farben von Galaxien (wenige Filter); Extremfall: ‘‘Dropouts‘‘ 2) Template Matching: Modellspektren/Spektren aus Archiven werden an Flussmessungen in Filtern angefittet 3) Empirische Methode: Spektren aus beobachteten Feld werden an Flussmessungen angefittet 1. Farben von Galaxien - Dropouts Klassische Methode: Suche nach elliptischen Galaxien. Flussdifferenzen zwischen 2 Filtern als Maß für den 4000 Å Break Hohes z: Suche nach Galaxien, die in einem oder mehreren Filtern keinen Fluss mehr zeigen Ly-limit RH = Rydbergkonstante 1 1 • = 1.097 • 107 m-1 Wasserstoffatom: λemitiert = RH 1 1 − 2 2 n = 1 - ∞, n2 > n1 n1 n2 n1 = 2 Balmerserie: n2 = 3 n2 = 4 = 6563 Å (H ) = 4861 Å (H ) n1 = 1 Lymanserie: n2 = 2 n2 = ∞ = 1215 Å (Ly ) = 912 Å (Ly-limit) Alle Photonen mit < 912 Å ionisieren Wasserstoff und werden sofort absorbiert!!! Dropout-Technik für Lyman-break Galaxien (Steidel, 1993) Theoretisch: U: z > 3 B: z > 4.4, V: z > 5.6 R: z > 6.7, I: z > 8.5 Problem: Ly -Wald, Absorption von Photonen speziell zwischen 912 Å und 1215 Å durch Wasserstoffwolken entlang Sichtlinie . U-Dropout aus dem FORS Deep Field U B (25.6mag) V (24.9mag) R (24.1mag) I (23.7mag) 2. Template Matching Anfitten von Galaxienspektren an Flussmessungen in 5+ Filtern, oft Kombination aus Breitband (UBVRI) + Mittel/Schmalbandfiltern z.B. COMBO-17 mittels Methode der kleinsten Quadraten ( 2) oder wahrscheinlichstes Spektrum (Maximum Likelihood). Wichtigste Charakteristika: Ly-limit und 4000 Å break, Kontinuumsverlauf generell (blau/rot), ev. Linien Entweder: beobachtete Spektren (z.B. Coleman 1980) oder Modellspektren von Synthesemodellen (Bruzual, 1983). Nachteil: Beobachtete Spektren lokal (kleines z), keine Entwicklung berücksichtigt, Modellspektren berücksichtigen Entwicklung variieren aber als Funktion der Inputparameter (z.b. Initial Mass Function IMF = Massenfunktion zu Beginn der Entwicklung) Trotzdem: Funktioniert erstaunlich gut!!! Photometrische Rotverschiebung - Ellipse Photometrische Rotverschiebung – Irreguläre Galaxie Rotverschiebungen: Vergleich spektroskopisch vs. photometrisch im FORS Deep Field 3. Empirische Methode Erweiterung der Template Matching Methode: Beobachtete Spektren im Feld werden als Template herangezogen, d.h. auch bei hohem z!!! Im Prinzip Idealfall, selten erfüllt Nachteil: Naturgemäß nur für hellere Objekt möglich (bei hohem z in der Regel > L∗), u.U.nicht repräsentativ Sloan Digital Sky Survey Generell gilt: Photometrische Rotverschiebungen sind nie so genau wie spektroskopisch ermittelte. Typischerweise: z (spektroskopisch): 0.001 z (photometrisch): 0.01-0.1 Vollständigkeit Kann ermittelt werden durch: a) Simulationen (siehe Radiodurchmusterungen) b) Konservativer Ansatz: ‘‘helles Limit‘‘ Nachteil: ev. nicht genügend Objekte für Leuchtkraftfunktion bzw. interessante schwache Objekte fallen weg c) Objektzählungen Annahme: Homogene Verteilung der Objekte im Raum (nicht immer erfüllt) M = B – 5 • log d - 25 ; d = Leuchtkraftentfernung (aus L = f • 4 d2) B - M = 5 • log d + 25; falls M fest B ~ 5 • log d d ~ 10 B/5 bemerkbar über: Änderung der Helligkeit macht sich im Volumen d ≈ (10 3 ∆B / 5 3 ) = 10 0.6• ∆B D.h. Vollständigkeit bis obige Beziehung nicht mehr erfüllt ist Galaxienzählung als Funktion von I = 0.5mag. Die Stichprobe ist vollständig bis ca. 22mag (aus Fried, 2001) d) V/ Vmax – Test: Traditioneller Test, Annahme wieder: gleichmäßige und homogene Verteilung der Objekte Prinzip: In einer vollständigen Stichprobe, welche Volumen Vmax umfasst, sind 50% der Objekte innerhalb Vmax/2 und 50% der Objekte innerhalb Vmax/2 - Vmax Jedes Objekt i wird innerhalb eines Volumen 4 / 3π • d i3 gefunden, 3 oder kann bis zu einem maximalen Volumen 4 / 3π • d max gefunden werden In einer vollständigen Stichprobe haben 50% der Objekte Vi/ Vmax < 0.5, und 50% Vi/ Vmax > 0.5 Vollständigkeit wird ermittelt durch tunen der scheinbaren Helligkeit B so, dass das mittlere Vi/ Vmax = 0.5 !!! Falls B zu hell: V/ Vmax < 0.5, d.h. hellere Galaxien sind leichter zu detektieren Falls B zu schwach: V/ Vmax ≤ 0.5!!!!! Falls Objekte homogen verteilt Anwendung: Bestimme für eine Stichprobe B so, dass V/ Vmax = 0.5. Selektiere dann eine Set aus der Stichprobe (z.B. QSOs) und führe den V/ Vmax – Test wieder durch. Beispiel: V/ Vmax > 0.5 Anzeichen für Entwicklung, d.h. QSOs sind häufiger bei großen z (Entfernungen) zu finden. Immer problematisch: Korrekturen die zur Bestimmung von B angebracht werden müssen, z.B. interstellare Extinktion, sind unsicher Es ist quasi unmöglich eine absolut vollständige Stichprobe aus einer Anzahl von Objekten herauszupicken!!!!! V/Vmax-Test für eine Stichprobe von Quasaren aus einem vollständigen Sample. Mittleres V/Vmax = 0.66 Anzeichen für Entwicklung Raumdichte und Leuchtkraftfunktion Annahme: Raumvolumen mit bestimmter Anzahl von Objekten, Volumen muss in Abhängigkeit von Epoche (z) betrachtet werden. Mitbewegte Raumdichte (co-moving density) entsprechend adjustiert Raumdichte von Objekten mit M*: Anzahl der Objekte pro Einheitsvolumen mit M* + 0.5 < M* < M* - 0.5 Tabuliert für verschiedene Werte M* Raumdichtefunktion Differentielle Funktion: (log L*) oder (M*) Integrierte Funktion: Aufsummierung aller Objekte > M* pro Einheitsvolumen Leuchtkraftfunktion Problem: Da Durchmusterungen immer flusslimitiert, muss das durchmusterte Volumen für jedes Objekt einzeln bestimmt werden, d.h. maximal durchmustertes Volumen muss über V/Vmax – Test bestimmt werden Die Leuchtkraftfunktion kann zur Untersuchung der Entwicklung von Objektklassen (z.B. als Funktion von z) herangezogen werden. Falls das Universum sich in einem ‘‘steady state‘‘ befinden würde, sollte sich die Leuchtkraftfunktion nicht ändern Die Leuchtkraftfunktion kann sich nur auf zwei Arten entwickeln, da zur Bestimmung der Leuchtkraftfunktion nur 2 Parameter eingehen: a) Leuchtkraftentwicklung b) Dichteentwicklung (oder auch Kombination von beidem). Leuchtkraftentwicklung: Helligkeit der Objekte ändert sich als Funktion von z Dichteentwicklung: Anzahl der Objekte ändert sich als Funktion von z Dichteentwicklung Leuchtkraftentwicklung Referenzen Butcher-Oemler Effekt: H. Butcher & A. Oemler, Astrophysical Journal, 1984, Vol. 285, S. 426 Lyman-break Galaxien: C. Steidel & D. Hamilton, Astronomical Journal, 1993, Vol. 105, S. 2017 Synthetische Spektren: A. G. Bruzual & S. Charlot, Astrophysical Journal, 1993, Vol. 405, S. 538 Beob. Spektren: G.D. Coleman et al., Astrophysical Journal Supplement, 1980, Vol. 43, S. 393 Sternbildungsrate: H. Hippelein et al., Astronomy & Astrophysics, 2003, Vol. 402, S.65 Galaxienzählungen/Leuchtkraftfunktion: J. Fried, Astronomy & Astrophysics, 2001, Vol. 367, S. 788 Photometrische Rotverschiebungen: I. Csabai et al., Astronomical Journal, 2003, Vol. 125, S. 580 V/Vmax-Test: D. Weedman, Quasar Astronomy, Kapitel 5/6 SDSS: www.sdss.org Galaxientyp-Spiel: www.usm.uni-muenchen.de/people/saglia/dm/galaxien/spiel/spiel/node4.html Photometrische Rotverschiebungen im HDF zum anklicken: bat.phys.unsw.edu.au/~fsoto/hdf/hdf_fs.html