Spezielle Themen der Mathematik: Reelle Zahlen, Folgen, Reihen

Westfälische Wilhelms-Universität Münster
Institut für Didaktik der Mathematik und der Informatik
Dr. Astrid Brinkmann
Spezielle Themen der Mathematik:
Reelle Zahlen, Folgen, Reihen, Funktionen
Warm-up Übungen 0
(Keine Abgabe dieser Übungen)
Mein teurer Freund, ich rat Euch drum
Zuerst Collegium Logicum.
Da wird der Geist Euch wohl dressiert,
In spanische Stiefeln eingeschnuert,
Dass er bedaechtiger so fortan
Hinschleiche die Gedankenbahn,
Und nicht etwa, die Kreuz und Quer,
Irrlichteliere hin und her.
(Goethe, „Faust“)
Aufgabe 1
In der Mathematik haben wir es mit Aussagen zu tun. Eine mathematische Aussage ist ein
sprachliches Gebilde, von dem prinzipiell feststeht, ob es wahr (w) oder falsch (f) ist (Aristoteles).
a)
Geben Sie an, welche der folgenden sprachlichen Gebilde Aussagen sind, und entscheiden Sie ggf., ob es sich um eine wahre oder eine falsche Aussage handelt.
(i) Jede Primzahl ist ungerade.
(ii) Jede Quadratzahl ist durch 2 teilbar.
(iii) Für alle m   1 existiert ein n   , so dass n  m .
(iv) Das Produkt dreier aufeinander folgender natürlicher Zahlen ist stets durch 6 teilbar.
(v) Es gibt eine rationale Zahl, die nicht reell ist.
(vi) 0, 9 ist gleich 1.
(vii) Die Gleichung x 2  5 x  6  0 hat zwei Lösungen in der Menge der ganzen Zahlen
.
(viii) Die Gleichung x 3  1  0 hat keine Lösung in der Menge der reellen Zahlen  .
1
m   steht für: m ist eine natürliche Zahl.
b) Formulieren Sie folgende Aussagen mit Hilfe von „Es gibt ...“ und „(Für) alle ...“.
1
Beispiel: Aus „Ist x eine reelle Zahl und x  0 , so ist  0 “ wird „Für alle x mit x  
x
1
und x  0 gilt  0 “.
x
(i) Politiker sind bestechlich.
(ii) Manche Politiker sind bestechlich.
(iii) Die Gleichung 3x  2 hat keine Lösung in  .
(iv) Ist  eine reelle Zahl  0 , so ist  2  0.
c)
Bilden Sie die Negation (d. h. die Verneinung) folgender Aussagen.
(i) Für alle reellen Zahlen   0   gilt (   ) 2  0 .
(ii)
Es gibt eine natürliche Zahl m, so dass n  m für alle natürlichen Zahlen n gilt.
Aufgabe 2
Es seien die folgenden Teilmengen von  gegeben:
M1 = {-4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9},
M2 = { z   z ist gerade und 0  z  7 },
M3 = { z   z  10 },
M4 = { z   es gibt ein y   mit z = y2},
M5 = { z   z = z2}.
Untersuchen Sie die gegebenen Mengen paarweise auf Inklusion und geben Sie Ihre Antwort
in Form einer Tabelle nach folgendem Muster:

M1
M2
M3
M4
M5
M1
1.1
1.2
1.3
1.4
1.5
M2
2.1
2.2
2.3
2.4
2.5
M3
3.1
3.2
3.3
3.4
3.5
M4
4.1
4.2
4.3
4.4
4.5
M5
5.1
5.2
5.3
5.4
5.5
Kreuzen Sie das Feld i.k an, wenn Mi  Mk gilt.
Aufgabe 3
Beweisen Sie durch vollständige Induktion über n.
a)
Für alle n   gilt: 20  21  2 2  ...  2n 1  2 n  1 .
b) Für alle n   gilt: 12  22  32  ...  n 2 
1
n( n  1)(2n  1) .
6
c)
Für alle n   gilt:
1
1
1
1
n


 ... 

.
1 2 2  3 3  4
n  (n  1) n  1
Aufgabe 4
Wir beweisen durch vollständige Induktion, dass alle Katzen die gleiche Augenfarbe haben:
Für n  1 ist die Behauptung offensichtlich.
Wir nehmen jetzt an, dass je n Katzen die gleiche Augenfarbe haben, und beweisen, dass das
auch für je n  1 Katzen gilt.
n Katzen

...
1. Katze
2. Katze
n 1
n
n 1

n Katzen
Bild 1
Wir nehmen n  1 willkürlich ausgewählte Katzen und nummerieren sie (Bild 1). Nach der
Induktionsvoraussetzung haben die Katzen mit den Nummern 1 bis n die gleiche Augenfarbe
und auch die n Katzen mit den Nummern 2 bis n  1 . Zu beiden Mengen gehört z. B. die Katze Nr. 2, also haben alle n  1 Katzen die gleiche Augenfarbe.
Wo steckt der Fehler?
Aufgabe 5
Betrachten Sie folgenden Textauszug aus
Maaß, Jürgen & Wildt, Michael. 2012. „Vernetzen lohnt sich: Nachhaltig Lernen hilft
Zeit sparen!“ In: Astrid Brinkmann (Reihenhrsg.). Astrid Brinkmann, Jürgen Maaß,
Hans-Stefan Siller, Matthias Brandl (Bandhrsg.). Mathe vernetzt – Anregungen und Materialien für einen vernetzenden Mathematikunterricht. Band 2. Aulis Verlag, S. 9–22.
ISBN 978-3-7614-2859-7.
zur Entdeckung der Irrationalität in Klasse 5/6 anhand von Zahlenrätseln und nehmen Sie dies
zum Anlass, Folgendes zu wiederholen:
 Unterschied zwischen rationalen und irrationalen Zahlen (auf Schulniveau),
 Quadratische Ergänzung bilden,
 Lösen quadratischer Gleichungen,
 Satz von Viëta,
 Faktorisieren quadratischer Terme.
Textauszug:
Jürgen: Irrationalität in Klasse 6? Das musst
du genauer erklären!
Michael: Ich gestalte in meinem Unterricht
in Klasse 5 eine Unterrichtseinheit zum
Thema ‚Zahlenrätsel’. Das Rätselformat ist
einfach: „Ich denke mir zwei Zahlen, die
addiert 7 und multipliziert 10 ergeben.
Kennst du die beiden Zahlen?“ Man kann
das, wie gesagt, schon in der Grundschule
beginnen, sobald die Rechenoperationen so
weit von den Lernenden beherrscht werden,
dass der Rechenwiderstand nicht zu groß ist.
Das Schöne daran ist: Solche Rätsel kann
sich jeder ausdenken – auch jemand, der sein
eigenes Rätsel nicht lösen könnte, wenn er es
gestellt bekommt. Man muss ja nur zwei
Zahlen als Lösungen nehmen und daraus das
Rätsel herleiten. Solche Rätsel zu erfinden
und zu lösen macht vielen unserer Gesamtschüler großen Spaß, denn damit kann
man absolut autonom arbeiten, in Partneroder Gruppenarbeit. Dabei werden jede
Menge Fehler gemacht. Und von selbst stellt
sich dabei heraus, dass sich nicht alle Rätsel
lösen lassen. Also gibt es in der ganzen Klasse Diskussionsbedarf, bei der eine formale
Notation absolut sinnvoll ist und sofort von
allen Beteiligten übernommen wird:
Suche a und b mit: a  b  7 und a  b  10 .
Wie man durch Versuch und Irrtum a und b
bestimmt, ist ein Thema, an dem sich Schüler/innen sehr verschieden lang abarbeiten
können, bis sie eine Strategie haben. Spannend wird es, wenn ein pfiffiges Mitglied der
Lerngruppe oder ich als Lehrkraft die Sache
vorantreibe:
- Suche a und b mit: a  b  7 und a  b  10
-
Suche a und b mit: a  b  7 und a  b  11
-
Suche a und b mit: a  b  7 und a  b  12
-
Suche a und b mit: a  b  7 und a  b  13
-
Suche a und b mit: a  b  7 und a  b  14
usw.
Das erste und das dritte Rätsel gehen. Die
anderen nicht. Aber es gibt Unterschiede:
Beim ersten Rätsel sind die beiden Zahlen 2
und 5. Beim dritten Rätsel sind die Zahlen 3
und 4. Also muss es doch für das zweite Rätsel zwei Zahlen geben, die zwischen 2 und 3
bzw. zwischen 4 und 5 liegen! Aber beim
Rätsel Nr. 5 ist es anders: Wenn ich für a
und für b 3,5 wähle und 3,5  3,5 ausrechne,
so komme ich nicht auf 14! 14 lässt sich also
nicht erreichen. Inzwischen hat nämlich sicher schon ein schnell denkendes Mitglied
der Gruppe herausgefunden, dass man
a  b  8 und a  b  100 niemals lösen kann,
denn auf mehr als auf die Hälfte von 8, mit
sich selbst malgenommen, kommt man nicht;
die Grenze, die man für den Multiplikationsteil des Rätsels erreicht, ist 16. Das ‚größte
lösbare Rätsel’ mit a  b  8 ist a  b  16 !
Es gibt also zwei Klassen von ‚nichtlösbaren
Rätseln’: die, die sich wohl lösen lassen
müssten, wenn man eine gebrochene Zahl
nimmt, und die, die man trotzdem nicht lösen
kann. Das ist ein schönes Ergebnis für starke
Schüler/innen in Klasse 5, und ein wunderbares Motiv für Lernende, sich Dezimalzahlen anzueignen, die ja in der Umwelt der
Fünftklässler sowieso ständig herumschwirren. Wie wäre es, wenn ich mal für das dritte
Rätsel a = 2,4 und b = 4,6 ausprobiere? Dann
ist ja a  b  7 , und a  b ist .... na, da brauchen wir in Klasse 5 eine Rechenregel für
das Multiplizieren von Dezimalzahlen, aber
die kann man ja bei einem Experten abfragen. Also wird mit viel Mühe herausgefunden, dass a  b  11, 04 ist. Das ist ja schon
haarscharf daneben, schon fast 11! Also
muss man weiter probieren, und mit etwas
Glück schafft man schon eine Lösung, die
die 11 auf vier Nachkommastellen erreicht.
Jürgen: Das alles in Klasse 5?
Michael: Ich habe immer Schüler/innen in
meinen fünften Klassen, die bei dem Thema
nicht nur anbeißen, sondern Funken sprühen.
Manche verbeißen sich in große Zahlen, wie
a  b  100 und a  b  2400 . Andere begeben sich eher in analytische Gefilde. Auf
jeden Fall wird Rechnen-Können zur gefragten Kompetenz, und das reicht – gemäß
Kernlehrplänen – für die Klasse 5. Die Irrationalität kommt dann in Klasse 6: Für den
Bruch 3/7 gibt es eine periodische Dezimalzahl. Die Lösungen von a  b  7 und
a  b  11 führen aber nicht auf eine Periode.
Zwar brechen beide Zahlen nach dem Komma nicht ab. Aber Periode und Rätsellösungszahlen verhalten sich verschieden. Bei
den Rätselzahlen muss man ewig und immer
weiter mittels ‚Versuch und Irrtum’ nach der
nächsten Ziffer suchen, und niemals kommt
man an eine Stelle, bei der man im Vorhinein
sicher sein kann, wie sie heißen wird. Das
gilt – so was können talentierte Sechstklässler selbst herausfinden und begründen: Das
Produkt zweier verschiedener Endziffern, die
sich auf eine Zahl mit der Endziffer 0 aufaddieren, ergibt keinesfalls eine Zahl mit der
Endziffer 0! Auf die gleiche Überlegung
stößt man übrigens auch, wenn man beim
Rätsellösen die Bruchzahlperspektive einnimmt. a und b können also keine Brüche
sein. Als Lehrer sage ich dann: Genau deshalb, weil man bei diesen Zahlen niemals auf
eine Regelmäßigkeit (wie beim Umwandeln
eines Bruchs in eine periodische Dezimalzahl) stößt, haben die Griechen diese Zahlen
‚unvernünftig’ genannt – wir sagen ‚irrational’. Wenn sich die Schüler/innen in Klasse
6 untereinander erklären, was der Unterschied zwischen einer periodischen Dezimalzahl und einer irrationalen Dezimalzahl
ist, dann ist das hundertmal so lernwirksam,
wie wenn ich früher im Mathe-E-Kurs Klasse 9 versucht habe, den Schüler/innen diesen
Unterschied zu erklären.
Und gleichzeitig lernen die Schüler/innen
dabei alles, was sie zum Faktorisieren von
quadratischen Gleichungen benötigen: Die
Zahlenrätsel sind ja nichts anderes als die
Bestimmung der Faktorisierungen zu
x 2  7 x  10 ,
x 2  7 x  11 ,
x 2  7 x  12 ,
x 2  7 x  13 und x 2  7 x  14 , liefern also
indirekt die Lösung von quadratischen Gleichungen. Wer das gelernt hat, der schafft
damit, unter Zuhilfenahme eines Taschenrechners, alle Analysis-GrundkursaufgabenRechnungen im Zentralabitur innerhalb von
2 Minuten mit hinreichender Genauigkeit,
einschließlich der nicht faktorisierbaren Fälle. Und die schneller lernenden Schüler/innen sind hochmotiviert, ein Verfahren
zu erarbeiten, um im Falle quadratischer
Gleichungen
den
Versuch-und-IrrtumAufwand des Probierens zu umgehen: Vor
diesem Hintergrund erscheint das Verfahren
des Faktorisierens durch quadratische Erweiterung als eine geniale Erfindung! Das ist
dann ‚Vernetzung’ beim Lernen!
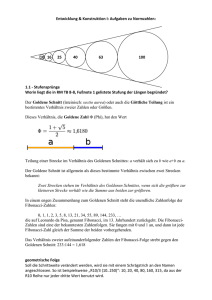
Aufgabe 6: Goldene-Schnitt-Zahl2
Was haben der Parthenon in Athen, eine Geige und das Rathaus in Leipzig gemeinsam?
An ihnen kann man ein besonderes Teilverhältnis entdecken, das als ästhetisch besonders ansprechend empfunden wird: den goldenen Schnitt oder das goldene Verhältnis. Es wurde in
der Antike und in der Renaissance häufig benutzt.
Was ist der goldene Schnitt?
Wenn eine Strecke so geteilt wird, dass die größere Teilstrecke zur kleineren im gleichen Verhältnis steht wie die Gesamtstrecke zur größeren Teilstrecke, dann sagt man: Die Strecke ist
nach dem goldenen Schnitt oder im goldenen Verhältnis geteilt.
a
2
b
Beim goldenen Schnitt gilt:
ab a

a
b
Diese Aufgabe ist zum Teil folgendem Buch entnommen:
Brinkmann, Astrid (2013): Die 111 schönsten Mathematikaufgaben für den Unterricht in der Sekundarstufe I mit
Lösungen. Aulis Verlag. ISBN 978-3-7614-2890-0.
a) Bestätigen Sie, dass der Turm des Leipziger Rathauses dieses (in etwa) nach dem
goldenen Schnitt teilt (s. Abbildung). Für
die Teilstrecken a und b gilt:
a = 55,62 m und b = 34,38 m.
Das Verhältnis von etwa 1,62, das sich in der
obigen Rechnung ergeben hat, ist für das goldene Verhältnis charakteristisch.
Wo findet man den goldenen Schnitt bei den anderen Beispielen?
Beim Parthenon teilt die Unterkante der Säulenauflage die Höhe des Tempels im goldenen
Schnitt.
Die Länge der Geige setzt sich aus der Länge des Resonanzkörpers und der Länge des Halses
zusammen. Der Teilpunkt zerlegt die Länge der Geige nach dem goldenen Schnitt.
b) Prüfen Sie das goldene Verhältnis beim Parthenon und bei der Geige, indem Sie die entsprechenden Strecken in den Abbildungen ausmessen. Weshalb kann man so vorgehen?
c) Berechnen Sie die Goldene-Schnitt-Zahl
a
(Bezeichnungen aus obigem Kasten), indem
b
ab a
 nach a auflösen und damit a in Abhängigkeit (als Vielfaa
b
ches) von b darstellen.
Sie die Gleichung
d)
Rechts sieht man das Emblem am Eingang
des Osnabrücker Zoos im Original, unten
eine Abbildung des Elefanten ohne Auge
und ohne Zwischenräume. Der Elefant ist
aus sechs immer kleiner werdenden Viertelkreisen zusammensetzt. Der Verkleinerungsfaktor von einem Radius zum nächsten ist immer gleich.
Bestimmen Sie den Verkleinerungsfaktor.
e) Das Freiburger Münster: der goldene Schnitt und noch mehr irrationale Zahlen in der Architektur3
Bei dem Freiburger Münster ist
zum einen die Länge des Münsters gleich der Höhe des Münsterturms ist (210 Ellen  116 m),
zum anderen sind beide Längen
im Verhältnis des goldenen
Schnitts geteilt, der Turm in
Turmschaft und Turmhelm, d. h.
die Strecke FS durch T2, und die
Münsterlänge durch Langhaus
und Chor, d. h. die Strecke AC
durch T1.
Interessant ist nun, dass die Baumeister der damaligen Zeit nicht die übliche Konstruktion,
die in allen Schulbüchern dazu gezeigt wird, verwendet haben, sondern der folgenden
Konstruktionsidee gefolgt sind:
„Zeichne ein Einheitsquadrat, trage von B aus über A bis G dessen Diagonale ab. Diese Länge
entspricht dem Langhaus. Zeichne über BD ein gleichseitiges Dreieck. Dessen Höhe entspricht dem Chor.“
Bestimmen Sie die Länge der roten Strecke EB und die der blauen Strecke FC und zeigen Sie:
Das Verhältnis Chor : Langhaus ist dabei fast genau gleich dem Kehrwert der Goldenen Zahl,
nämlich etwa 0,612! Ein merkwürdiger Zufall!(?)
3
Quelle: Brinkmann, Astrid; Bürker, Michael (2011): Bericht des Arbeitskreises „Vernetzungen im Mathematikunterricht“. http://www.mathematik.tu-dortmund.de/ieem/bzmu2011/_BzMU11_3_Arbeitskreise/BzMU11_AKVernetzung-BRINKMANN.pdf
Wissenswertes über den goldenen Schnitt
Bei antiken Statuen teilt der Bauchnabel die Körperlänge ungefähr
nach dem goldenen Schnitt. Der Amerikaner Frank A. Lonc will bei
65 Frauen nachgemessen haben, dass dies heute noch zutrifft. Auch bei anderen Körperverhältnissen soll der goldene Schnitt auftauchen,
nämlich am Kopf (Teilpunkt sind die Augenbrauen) und am Arm
(Teilpunkt ist der Ellenbogen), vgl. die Abbildungen.
Leonardo da Vinci skizzierte „Der Mensch nach Vitruv”, ein Proportionsschema der menschlichen Gestalt, in dem ebenfalls der goldene Schnitt auftaucht. (Vitruv war ein römischer Architekt, der den menschlichen Körper mit Kreis und Quadrat in Zusammenhang brachte.)
Noch ein paar goldige Verhältnisse: Legt man ein Rechteck um ein Hühnerei, entsteht oft ein
goldenes Rechteck (unten ist erklärt, was man darunter versteht). Auch die Front des UNOGebäudes in New York und (wieder einmal) des Parthenons in Athen bilden ein goldenes
Rechteck.
Was sind goldene Rechtecke?
Bei goldenen Rechtecken stehen die Seitenlängen a und b im goldenen Verhältnis. Viele Menschen empfinden diese Rechtecke als besonders harmonisch und schön.
Übrigens: Psychologen wollen herausgefunden haben, dass Kunden unbewusst Produkte bevorzugen, deren Verpackung an ein goldenes Rechteck erinnert.