Optik 05 - Martin Brennscheidt

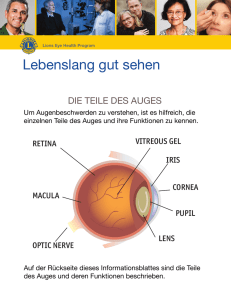
7.7 Auflösungsvermögen optischer Geräte und des Auges
Beim morgendlichen Zeitung lesen kann ein gesundes menschliche Auge die Buchstaben des Textes
einer Zeitung in 50cm Entfernung klar und deutlich wahrnehmen und den Text lesen. Erhöht man die
Entfernung zur Zeitung, so wird das Lesen des Textes bereits schwieriger und nur die Überschriften
sind noch gut lesbar. Entfernt man sich noch weiter so wird der Text zu einer verschwommenen
grauen Fläche
[34] Zeitungsartikel
Ursache hierfür ist das begrenzte Auflösungsvermögen des Auges. So kann das Auge ab einer
bestimmten Entfernung bzw. genauer ab einem bestimmten Sehwinkel zwei Gegenstände nicht
mehr getrennt voneinander wahrnehmen bzw. auflösen. Unter dem Sehwinkel versteht man den
Winkel zwischen den Lichtstrahlen die von den beiden Gegenständen ins Auge treffen.
Entfernt man sich von den Gegenständen (z.B. den Buchstaben der Zeitung), so wird der Winkel
zwischen ihnen kleiner und umgekehrt. In einem einfachen Experiment kann das maximale Auflösungsvermögen des Auges gemessen werden. Hierzu betrachtet man auf einem Blatt Papier
aufgedruckte senkrechte schwarze Streifen die jeweils eine Dicke und einen Abstand von
besitzen.
Nun entfernt man sich so weit vom Blatt Papier, bis man die einzelnen Striche gerade nicht mehr
getrennt wahrnehmen kann. Misst man diese Entfernung , so kann mit Hilfe des Tanges der
Sehwinkel berechnet werden unter dem zwei Gegenstände gerade noch vom Auge aufgelöst werden
können.
© M.Brennscheidt
Beispiel:
,
In diesem Kapitel soll die Ursache für das begrenzte Auflösungsvermögen des Auges und anderer
optischer Geräte untersucht werden. Hierzu soll zunächst der Aufbau des Auges näher betrachtet
werden: Das menschliche Auge ist vereinfacht dargestellt nichts anderes als eine Abbildungslinse die
gemäß den Linsengleichungen Gegenstände stark verkleinert auf der Netzhaut abbildet. Über den
Sehnerv werden die empfangenen Bildsignale an das Gehirn weitergeleitet.
[35] Auge
Um Gegenstände in unterschiedlichen Entfernungen scharf abbilden zu können, ist die Linse des
Auges flexibel gestaltet und kann durch einen Ringmuskel verändert werden. Der Ringmuskel kann
die Krümmung der Linse so verändern, dass sich die Brennweite der Linse der jeweiligen Entfernung
eines Gegenstandes anpassen kann. Vor der Linse befindet sich die Pupille bzw. die Eintrittsöffnung
des Auges, die durch eine Irisblende verkleinert bzw. vergrößert werden kann. Die Irisblende dient
dabei der Regulierung der Helligkeit. So ist die Pupille am Tag bei Sonnenschein sehr klein und in der
Nacht bei Dunkelheit sehr weit geöffnet.
Das begrenzte Auflösungsvermögen des Auges kann auf die Größe der Pupille zurückgeführt werden.
So kann man mit einem Fernrohr, das ein im Vergleich zur Pupille sehr großes Okular besitzt, auch
noch sehr weit entfernte Gegenstände auflösen, die mit dem Auge nicht mehr getrennt voneinander
wahrgenommen werden können.
© M.Brennscheidt
Schlussfolgerung: Es gibt einen direkten Zusammenhang zwischen dem Auflösungsvermögen und der
Größe der Eintrittsöffnung bei optischen Geräten. Allgemein gilt: „Je größer die Eintrittsöffnung,
desto besser ist das Auflösungsvermögen“.
Dieser Zusammenhang zwischen Auflösungsvermögen und Eintrittsöffnung kann mit Hilfe der
Wellenoptik erklärt werden. Da die Eintrittsöffnungen von optischen Geräten in der Regel rund sind,
soll nun im Folgenden die Beugung und Interferenz an einer kreisförmigen Öffnung untersucht
werden.
7.7.1 Beugung und Interferenz an einer kreisförmigen Öffnung
Experiment: Mit einem Laser wird eine kreisförmige Lochblende beleuchtet. Auf einem Schirm hinter
der Lochblende ist ein typisches Interferenzmuster mit einem hellen Zentrum und nach außen hin
abwechselnd dunklen und hellen Ringen zu erkennen.
Betrachtet man vom Interferenzmuster nur einen schmalen Streifen, so ähnelt das Interferenzmuster
der kreisförmigen Öffnung dem eines Einzelspalts.
Die Entstehung der Maxima und Minima an einer kreisrunden Öffnung kann deshalb analog zum
Einzelspalt durch die Interferenz von Huygenschen Elementarwellen hinter der Öffnung erklärt
werden. Im Gegensatz zum Spalt ergibt sich aus Symmetriegründen an einer kreisförmigen Öffnung
jedoch ein kreisförmiges und kein streifenförmiges Interferenzmuster.
Für die Auslöschung, also für Beugungsminima gilt beim Einzelspalt die Bedingung:
© M.Brennscheidt
Der Spaltbreite entspricht an der kreisförmigen Öffnung der Durchmesser der Lochblende . Für
Beugungsminima an der kreisförmigen Öffnung müsste demnach die Bedingung
gelten. Bestimmt man jedoch in einem Experiment mit einem Laser bekannter Wellenlänge den
Radius der Beugungsscheibchen und den Beugungswinkel, so ergeben sich für die Beugungsordnung
n keine ganzen Zahlen. Stattdessen gilt für die Minima:
Folgerung: Eine kreisförmige Öffnung verhält sich nur in grober Näherung wie ein beugender Spalt.
7.7.2 Das Auflösungsvermögen
Betrachtet man mit dem Auge einen näherungsweise punktförmigen Gegenstand, wie zum Beispiel
einen weit entfernten Stern, so gelangt das Licht des Sterns durch die kreisförmige Pupille auf die
Netzhaut.
[36] Sternbild Orion
Aufgrund von Beugung und Interferenz an kreisförmigen Öffnungen entsteht auf der Netzhaut ein
mikroskopisch kleines kreisförmiges Interferenzmuster, das vom menschlichen Gehirn als punktförmige Lichtquelle interpretiert wird.
© M.Brennscheidt
Betrachtet man einen zweiten Stern in einiger Entfernung vom ersten Stern, so entsteht an einer
anderen Stelle auf der Netzhaut ebenfalls ein kleines kreisförmiges Interferenzmuster. Das
menschliche Gehirn registriert zwei getrennte Lichtquellen.
Problematisch wird es, wenn die zwei Sterne sehr nah beieinander liegen. Ist dies der Fall, so kann
das Interferenzmuster des einen Sterns in den Bereich des Musters des anderen Sterns gelangen und
die beiden Muster überlagern sich.
© M.Brennscheidt
Liegen die Sterne so eng beieinander, dass die beiden Maxima ineinander übergehen, so kann das
Gehirn die beiden Sterne nicht mehr getrennt voneinander wahrnehmen und geht nur noch von
einer einzelnen Lichtquelle aus.
Ergebnis: Zwei Gegenstände bzw. Lichtquellen können dann gerade noch aufgelöst werden, wenn
sich die Intensitätskurven der zentralen Beugungsmaxima unterhalb der Hälfte ihrer Maximalintensität schneiden.
In diesem Grenzfall liegt das Hauptmaximum von beiden Interferenzmustern jeweils auf dem ersten
Beugungsminimum des anderen. Für die maximale Auflösung des Auges gilt somit die Formel:
Dabei ist
der minimale gerade noch auflösbare Sehwinkel und der Durchmesser der Pupille.
Vergrößert man den Durchmesser der Pupille, so verkleinert sich der kritische Sehwinkel und das
Auflösungsvermögen wird besser. Aus diesem Grund können weit entfernte Objekte mit einem
Fernrohr mit einem großen Objektivdurchmesser viel besser aufgelöst werden als mit einem Auge
mit einer kleinen Pupille.
Abschließende Bemerkung:
In vielen Büchern ist für das Auflösungsvermögen die Formel
angegeben. Dies ist zulässig, da für kleine Winkel der Sinus eines Winkels dem Winkel selbst
entspricht:
Diese Beziehung kann sehr einfach mit dem Taschenrechner durch Einsetzen kleiner Winkel
überprüft werden. Die Winkel müssen hierzu im Bogenmaß eingegeben werden (Taschenrechner von
DEG auf RAD umstellen!!!).
© M.Brennscheidt