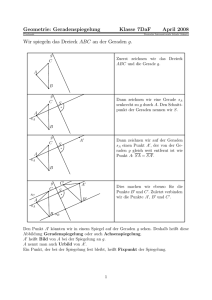
Winkel, Abstände, Spiegelung

Abiturkurs
Einheit 6: Winkel, Abstände, Spiegelung und
Projektion
Michael Göthel
15. April 2017
1 Winkel
1.1 Zwischen zwei Vektoren
Der Winkel zwischen zwei Vektoren folgt direkt aus der Definition des Skalarprodukts (siehe auch im Tafelwerk!):
u
v
#»
#»
a◦ b
cos γ = #» #»
|a| · | b |
Die Winkel aller anderen geometrischen Objekte folgt direkt aus dieser Definition, es muss lediglich überlegt werden welche Vektoren für die Berechnung
verwendet werden.
Achtung: bei der Verwendung der Formel kommt immer der kleine Winkel heraus!
1.2 Zwischen zwei Geraden
Verwenden der Richtungsvektoren
der beiden Geraden für die Berechnung
des Winkels:
#» #» mg ◦ mh cos γ = # » # » |mg | · |mh |
1.3 Zwischen zwei Ebenen
Verwenden der Normalenvektoren
der beiden Ebenen für die Berechnung
des Winkels:
#» #» n1 ◦ n2 cos γ = # » # » |n1 | · | n2 |
1.4 Zwischen Geraden und Ebenen
Verwenden des Normalenvektors der
Ebene und des Richtungsvektors der
Gerade für die Berechnung des Winkels
(Sinus verwenden!):
#» # » n ◦ mg sin γ = #» # » | n | · |mg |
Welcher Winkel?
Bei den Formeln für den Winkel zwischen Geraden und Ebenen sorgt der
Betrag dafür, dass immer der kleine Winkel berechnet wird. (γ ≤ 90◦ !)
u
v
2 Abstände
Für alle Abstände sind die Vorgehensweisen für die Fälle Punkt-Gerade und Punkt-Ebene wichtig!
Die Berechnung der Abstände für alle anderen Fälle kann auf diese beiden zurück geführt
werden!
2.1 Abstand Punkt-Gerade
Der Abstand eines Punktes zu einer Geraden kann über eine Formel berechnet werden:
# »
# » × AP
# » = Richtungsvektor der Geraden, A = Aufpunkt der Geraden,
|m
|
m
g
g
d=
# »|
P = Punkt zu dem der Abstand zu berechnen ist
|m
g
2.2 Die Hessesche Normalform der Ebene
Wenn die Ebene in der Koordinatenform gegeben ist, so kann die Ebene als Hessesche Normalform
geschrieben werden:
E:
Ax + By + Cz − D
=0
| #»
n|
Alternativ kann auch die Form in der Vektorschreibweise verwendet werden:

  
x − Ax
nx
 y − Ay  ◦  n y 
z − Az
nz
E:
=0
#»
|n|
2.3 Abstand Punkt-Ebene
Der Abstand eines Punktes zu einer Ebene kann durch Einsetzen des Punktes in die Hessesche
Normalform errechnet werden. Der dabei ausgerechnete Wert ist der Abstand zur Ebene:
Ax + By + Cz − D =d
| #»
n|
Beispiel: E : 3x + 2y − 5z = 9, P = (1,2,3)
3·1+2·2−5·3−9
√
√
HNF: 3x+2y−5z−9
=
0
⇒
d
=
38
38
−17
= |√
| = 2,75LE
38
2.4 Alle anderen Abstände
Alle anderen Abstände können auf die Fälle Punkt-Ebene und Punkt-Gerade zurück geführt werden:
1. Abstand windschiefer Geraden:
Reduktion auf den Fall Punkt-Ebene! Die Ebene wird durch eine Gerade mit dem angehängtem
Richtungsvektor der zweiten Gerade gebildet. Der Punkt ist der Aufpunkt der zweiten Gerade.
2. Abstand paralleler Geraden:
Reduktion auf den Fall Punkt-Gerade! Der Abstand des Aufpunktes der einen Geraden ist die
Entfernung der ganzen Geraden.
3. Abstand Gerade-Ebene: Reduktion auf den Fall Punkt-Ebene! Der Punkt ist der Aufpunkt
der Geraden. Das funktioniert natürlich nur, wenn Gerade und Ebene parallel sind, sonst
ist der Abstand 0.
4. Abstand paralleler Ebenen:
Reduktion auf den Fall Punkt-Ebene! Der Punkt ist der Aufpunkt der anderen Ebene.
3 Projektion und Spiegelung
3.1 An Koordinatenebenen
Projektion
Spiegelung
Punkt
Entsprechende Koordinate null setzen!
Bei entsprechender Koordinate Vorzeichen wechseln!
Gerade
Im Aufpunkt und im Richtungsvektor die entsprechende Koordinate null
setzen!
Im Aufpunkt und im Richtungsvektor bei der entsprechenden Koordinate
das Vorzeichen wechseln!
3.2 An beliebigen Ebenen
1. Punkte:
• Aufstellen einer Geraden mit dem Punkt und dem Normalenvektor der Ebene
• Durchstoßpunkt mit der Ebene berechnen (man erhält den Parameter r der Geraden)
⇒ Projektion des Punktes!
• Den bei der Berechnung des Durchstoßpunktes erhaltenen Parameter r verdoppeln und
in die Gerade einsetzen ⇒ Spiegelung des Punktes!
P
P
P*
2. Geraden:
• Projektion und/oder Spiegelung des Aufpunktes der Geraden berechnen (siehe 1.)
Hinweis: Wenn der Aufpunkt der Durchstoßpunkt mit der Ebene sein sollte, dann einen
beliebigen Punkt auf der Gerade bestimmen und dessen Projektion und/oder Spiegelung
ermitteln.
• Durchstoßpunkt der Geraden mit der Ebene ermitteln
• Projektion: Gerade zwischen Durchstoßpunkt und der Projektion.
Spiegelung: Gerade zwischen dem Durchstoßpunkt und der Spiegelung.
• Hinweis: bei einer parallelen Geraden 2 beliebige Punkte Projizieren/Spiegeln für die
entsprechende Gerade
A
g
D
A
g*
A*
g