Sinus-Oszillator mit 3 RC-Gliedern, Simulation mit Tephys und mit

Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsytemtechnik,
A:\sinus\sinosz2.doc,
Seite 1/7
Sinus-Oszillator mit 3 RC-Gliedern,
Simulation mit Tephys und mit Simulink.
Wahlweise Fremderregung oder Selbsterregung
Umax
R1
R3
R2
C1
C2
u1
R4
C3
u2
u3
Op1
R5
uA
u3
Op2
Umin
Spannungsfolger
invert. Verstärker,
V= - R5/R4
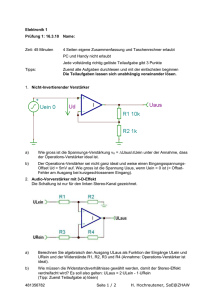
Diese Schaltung stellt einen Sinus-Oszillator dar. Da die Schaltung außer den Verstärkern nur Widerstände
(R ) und Kondensatoren (C) enthält, spricht man auch von einem RC-Sinus-Oszillator (oder RC-SinusGenerator oder einfach RC-Generator).
Man mag sich wundern, wieso damit Sinus-Schwingungen entstehen. Denken wir an eine mechanische
Wanduhr (Pendeluhr) aus Opas Zeiten: da drin ist ein mechanischer Schwinger, ein „Schwerependel“, oder
bei einer Taschenuhr ein „Drehschwinger“ . Damit ein solcher mechanischer Schwinger Dauerschwingungen
ausführt, braucht man „nur“ das bisschen Energieverlust, das infolge Reibung entsteht, zu ersetzen. Diese
vergleichsweise winzige Zusatz-Energie wird aus einem Energievorrat abgerufen. Bei der Pendeluhr ist der
Energievorrat ein gehobenes Gewicht, bei der Drehschwinger-Uhr eine gespannte Feder.
Die Kunst der Uhrmacher besteht darin, im richtigen Moment dem schwingenden System aus diesem
Energievorrat etwas Energie zu zuführen. Dieser Mechanismus ist alles andere als trivial!! -- Auch ohne diese
Energiezufuhr schwingt ein Pendel nach einmaligem Auslenken und dann Loslassen viele Perioden lang
sinusförmig weiter. Allerdings wird die Amplitude allmählich kleiner.
Bei obiger RC-Schaltung ist das total anders: Ein RC-Glied „denkt“ nicht daran, von alleine zu
schwingen. Auch drei hintereinander geschaltete RC-Glieder schwingen nicht die Spur sinusähnlich, wenn man
keinen geeigneten Verstärker nimmt. Im Gegensatz zu den erwähnten mechanischen Uhren ist also bei einem
RC-Oszillator der Verstärker dringend nötig. Das soll durch nachfolgende Überlegung vertieft werden:
1
2
Umax
uEin
R1
R3
R2
R4
u0
C1
u1
C2
u2
C3
u3
R5
uA
u3
Op1
Spannungsfolger
Op2
Umin
invert. Verstärker,
V= - R5/R4
Dazu haben wir die ursprüngliche Schaltung etwas verändert: Die „Rück-Kopplungs-Leitung“ vom Ausgang
des OP2 zum Widerstand R1 ist unterbrochen worden. Stattdessen ist ein Schalter eingefügt worden. In der
Schalterstellung 2 haben wir die ursprüngliche Schaltung (mit „Rück-Kopplung“, also „Selbsterregung“), in
Schalterstellung 1 wirkt hingegen die Spannung u0 einer externen Spannungsquelle. Statt Selbsterregung
haben wir bei Schalterstellung 1 „Fremderregung“.
Denken wir uns Experimente mit dieser Fremderregung durchgeführt. u0 sei Sinus. Das 1. RC-Glied (R1,
C1) ist ein Tiefpass, ebenfalls sind die anderen RC-Glieder (R2,C2, R3, C3) Tiefpässe. Wie wir wissen, ist der
Ausgang eines Tiefpasses nacheilend im Phasenwinkel (verglichen mit dem Phasenwinkel des Eingangs u0).
Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsytemtechnik,
A:\sinus\sinosz2.doc,
Seite 2/7
Ein Tiefpass 1. Ordnung (also aus nur einem RC-Glied) macht maximal Phasen-Nacheilung von 90 Grad,
folglich machen 3 hintereinandergeschaltete Tiefpässe maximal 3 * 90 Grad = 270 Grad Phasen-Nacheilung.
Ein elektronischer Verstärker hat (im einfachsten Fall) entweder keine Phasenverschiebung (dann ist er ein
„nicht-invertierender“ Verstärker) oder er macht 180 Grad Phasenverschiebung. Dann ist er ein
„invertierender“ Verstärker.
Wollen wir aus obigen 3 hintereinander geschalteten Tiefpässen einen Sinus-Oszillator bauen, so müssen
wir einen invertierenden Verstärker nehmen (also 180 Grad Phasenverschiebung). Verändern wir, von kleinen
Frequenzen anfangend, die Frequenz der Sinus-Spannung u0 und beobachten wir zunächst die Spannungen
u0 und u3. Wie erwartet, wird mit wachsender Frequenz die Amplitude der Spannung u3 kleiner (weil es ja ein
Tiefpass ist) und um so mehr phasen-nacheilend (gegenüber u0), je größer die Frequenz ist. Aber mehr als
3*90 Grad kann u3 nicht nacheilen, s.o. Interessant zum Aufbau eines Sinus-Oszillators ist nur die PhasenNacheilung von 180 Grad. Nennen wir die zugehörige Frequenz f180 und die zugehörige „Abschwächung“
A180, soll heißen A180 = Amplitude von u0 dividiert durch die Amplitude von u3 (bei 180 Grad).
Betrachten wir jetzt die Ausgangs-Spannung uA. Zunächst überzeugen wir uns, dass uA (wie verlangt)
„invertiert“ ist gegenüber u3 ist, also 180 Grad phasenverschoben. Jetzt spätestens ahnt man, worauf wir
hinauswollen: Bei der oben festgestellten Frequenz f180 ist zwar u3 um 180 Grad nacheilend, aber uA ist bei
genau dieser Frequenz gleichphasig mit u0. Stellen wir jetzt den Verstärkungsfaktor des Op2 so ein, dass
die Abschwächung infolge der 3 Tiefpässe gerade aufgehoben wird, so ist die Ausgangs-Spannung uA
nicht nur phasengleich mit der externen Sinusspannung u0 sondern hat auch die gleiche Amplitude. Der
fragliche Verstärkungsfaktor muss A180 betragen(s.o). Legen wir jetzt den Schalter in Stellung 2, so wird die
Sinus-Schwingung „selbsterregt“ weiter schwi ngen. Mit welcher Frequenz? Mit genau derjenigen Frequenz,
bei der die Phasenverschiebung von u3 genau 180 Grad ist, also mit unsrer obigen Frequenz f180.
Für gleiche Werte R1=R2=R3=R und C1=C2=C3 =C ergibt sich nach nicht ganz leichter Rechnerei
die Frequenz bei 180 Grad Phasen-Nacheilung f180 = sqrt(6) / (2*pi*R*C) und die zugehörige
Abschwächung um den Faktor A180 = 29.
Der Verstärker muss also bei Selbsterregung den Verstärkungsfaktor V = - 29 haben.
Dies aufregende Experiment mit der externen Sinus-Schwingung u0 und Beobachten von u3 bzw. uA und
Umschalten auf Selbsterregung wollen wir zunächst mit Tephys simulieren und anschließend mit Simulink:
Simulation mit Tephys:
Aufstellen der DGLn und Tephys-Algorithmus:
Strom durch R1 = Strom durch Kondensator C1 + Strom durch R2 -->
(uEin- u1)/R1 =
C1 * du1/dt
+ (u1- u2)/R2 -->
Algorithmus nach dem einfachen Prinzip neuer Wert u1 = alter Wert u1 plus die Änderung von u1,
--> u1 =u1 + ((uEin – u1)/R1 - (u1 – u2)/R2 ) *dt/C1 (Zeile 6)
Strom durch R2 = Strom durch C2 + Strom durch R3 -->
(u1-u2)/R2 = C2*du2/dt
+ (u2-u3)/R3 --> u2 = u2 + ((u1-u2)/R2 – (u2-u3)/R3 ) *dt/C2 (Zeile 7)
Strom durch R3 = Strom durch C3 -->
(u2 – u3 )/R3 =
C3 * du3/dt --> u3 =u3 + ((u2-u3)/R3 )* dt/C3 (Zeile 8)
----------------------- D:\KUELLMAR\MATLAB\SI3RCS1.TXT ---1¦ ext = ja(tex-t) { ext ist 1 bis t=text, ab dann ext=0 }
2¦ w = wSt+(wE-wSt)*t/Tmax { w = Kreisfrequenz (gelesen omega).
w startet mit dem Wert wSt und geht in der Zeit Tmax auf den Endwert wE}
3¦ wink = wink+w*dt { wink= “Winkel” = Zeitintegral der Kreisfrequenz w}
4¦ u0 = sin(wink) { u0 = Sinus mit der MomentanKreisFrequenz w}
5¦ uEin = ja(ext)*u0+nein(ext)*uA { uEin ist die Spannung am Widerstand R1, s. Figur}
6¦ u1 = u1+((uEin-u1)/R1-(u1-u2)/R2)*dt/C1 { u1 = Spannung am Kondensator C1}
7¦ u2 = u2+((u1-u2)/R2-(u2-u3)/R3)*dt/C2 { u3 = Spannung am Kondensator C2 }
8¦ u3 = u3+((u2-u3)/R3)*dt/C3 { u3 = Spannung am Kondensator C3 }
9¦ uA = begr(V*u3,max,min) { uA = Spannung am Ausgang von OP2. Verstärkung V ist negativ! }
10¦ t = t+dt { Wichtig: der Parameter Tmax muss eingegeben werden, er ist NICHT identisch mit tmax}
Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsytemtechnik,
A:\sinus\sinosz2.doc,
Seite 3/7
Fig. 1 Fremderregung mit u0 (bis t = tex=35). Man erkennt, dass bei w ca. 2.448 uA phasengleich ist mit
u0. Da V= - 29 „richtig“ gewählt wurde, hat uA gleiche Amplitude wie u0. Ab t=tex=35 Selbsterregung.
Man erkennt, dass Amplitude uA (und u3) ab dann konstant bleiben
Fig. 2. V= - 32, also zu groß, drum ansteigende Amplitude bei Selbsterregung
Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsytemtechnik,
A:\sinus\sinosz2.doc,
Seite 4/7
Fig. 3. V= -26, also zu klein, drum Abnahme von uA (und u3) bei Selbsterregung.
Fig. 4. V= -100 also VIEL zu groß. Drum geht bei Selbsterregung uA in Begrenzung. Dennoch bleibt u3
(nahezu) sinusförmig. Das liegt daran, dass die „Oberschwingungen“ in uA durch die Tiefpasswirkung
der RC-Glieder stark geschwächt werden.
Simulation mit Simulink (Matlab 5.3):
Sinus-Oszillator mit 3 RC-Gliedern und invertierendem
Datei sinosz10.mdl
Verstärker V. Wahlweise extern oder rückgekoppelt
Aufruf mit
wSt + (wE-wSt) * u/ tmax
t
sinosz10parx, x=1,2
1/s
sin ( u )
u0
w
Fcn
uEin
tex > u
1/R1
Switch
1/C1
1/s
ext
Tephys: Si3RCS1.txt
ext = ja(tex-t)
u1
w = wSt+(wE-wSt)*t/Tmax
wink = wink+w*dt
u0 = sin(wink)
1/R2
uEin = ja(ext)*u0+nein(ext)*uA
1/C2
1/s
u1 = u1+((uEin-u1)/R1-(u1-u2)/R2)*dt/C1
u2 = u2+((u1-u2)/R2-(u2-u3)/R3)*dt/C2
u2
u3 = u3+((u2-u3)/R3)*dt/C3
uA = begr(V*u3,max,min)
1/R3
t = t+dt
V
1/C3
uA
1/s
max, min
u3
Der Tephys-Programm-Text ist mit in die Simulink-Schaltung „eingefügt“ worden. Dadurch kann man die
Konstruktion der Simulink-Schaltung verstehen: Sie ist „wörtlich“ übersetzt aus dem Tephys-Programm:
Betrachten wir die Kreisfrequenz w: In Tephys: w=wSt+(wE-wSt)*t/Tmax. Im „Funktionsblock“ Fcn steht
wSt + (wE-wSt) * u/tmax. Bekanntlich muss die Eingangsvariable innerhalb des Blockes die Bezeichnung u
haben. Also bedeutet hier u = t (wie bei Tephys) . Der Ausgang aus dem Block ist die Kreisfrequenz w. w
wird zeitlich integriert. Der Block 1/s ist ein Integrator.
Anschließend wird in einem weiteren Fcn-Block u0= sin(u) gebildet. In Tephys ist das nahezu wörtlich das
Gleiche: wink = wink + w*dt (also das Zeitintegral der Kreisfrequenz w), anschließend u0 = sin (wink).
Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsytemtechnik,
A:\sinus\sinosz2.doc,
Seite 5/7
Ähnlich wie in Tephys wird die Variable ext bebildet: in Tephys: ext = ja (tex –t), also ist ext = 1 für tex > t,
anschließend text =0. In Simulink: Die Zeit t geht aus der Uhr in einen weiteren Fcn-Block. Darin steht tex > u.
Dieser „Vergleich“ liefert den Wert „wahr“ =1 (also = 1 für tex > t ) bzw. den Wert „falsch“ = 0 wenn tex < t).
Der Schalter „switch“ hat 3 Eingänge, der mittlere ist der „Steuereingang“, hier also ext. Wenn ext >
Schwelle (hier Schwelle auf 0.5 gesetzt), dann wird der obere Eingang durchgeschaltet (hier also u0). Wenn
ext < Schwelle, dann wird der untere Eingang (hier also uA) durchgeschaltet.
In Tephys klingt das so: uEin = ja(ext)*u0 + nein(ext) * uA.
Jetzt u1: in Tephys u1 = u1+( (uEin - u1)/R1 - (u1-u2) / R2 )* dt/C1. ( vgl. auch die Herleitungen der DGLn,
s.o.)
Betrachten wir Simulink: Es wird die Differenz uEin- u1 gebildet. Diese Differenz wird mit dem konstanten
Faktor 1/R1 multipliziert (das Symbol Dreieck= „gain“). Ausgang aus dem gain ist also (uEin- u1)/R1.
Weiterhin wird die Differenz u1 - u2 gebildet, diese geht in den gain 1/R2, es entsteht also (u1 - u2 )/ R2.
Diese beiden gain-Ausgänge gehen in einen Subtrahierer, dessen Ausgang mit 1/C1 multipliziert wird.
Der Ausgang aus diesem gain 1/C1 hat also den Wert ( (uEin-u1)/R1 - (u1-u2)/R2 )* 1/C1. Dieser Wert wird
zeitintegriert und liefert die Variable u1. Das ist also „wörtlich“ wie in Tephys.
In entsprechender Weise werden die Variablen u2 und u3 gewonnen.
In Tephys:
u2 = u2+ ( (u1-u2)/R2 - (u2-u3)/R3 )* dt/C2
u3 = u3+ ( (u2-u3)/R3 )* dt/C3
Der Ausgang u3 wird multipliziert mit dem Verstärkungsfaktor V, dann kommt ein Begrenzer („saturation“)
mit oberem Wert max und unterem Wert min. Dessen Ausgang ist uA
in Tephys: uA = begr(V*u3,max,min)
Damit haben wir erkannt, dass die Simulink-Schaltung die „wörtliche“ Übersetzung aus Tephys ist.
Jetzt die Bilder 1 bis 4, die mit der weiter unten beschriebenen Methode
aus der Simulink-Schaltung entstanden sind.
Die Parameter dieser Bilder 1 bis 4 sind identisch mit den Parametern der
obigen Tephys-Figuren Fig. 1 bis Fig. 4
4
Bild=1,R1=1, C1=1, R2=1, C2=1, dt=0.01, R3=1, C3=1, V=-29, text=35
3
uA
u3*5
w
uA
u0
2
u0
w
ext/2
ext/2
u3*5
1
0
-1
hier uA und u0 gleichphasig
und gleiche Amplitude
-2
0
5
10
15
20
25
30
35
40
45
50
Bild 1: V= -29, also „richtig“. Man erkennt den Bereich, wo u0 und uA gleichphasig sind (s. Text im Bild)
Da V = -29 richtig ist, bleibt bei Selbsterregung (ab t =35) die Amplitude uA (und u3) konstant
Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsytemtechnik,
A:\sinus\sinosz2.doc,
Seite 6/7
4
uA
Bild=2,R1=1, C1=1, R2=1, C2=1, dt=0.01, R3=1, C3=1, V=-32, text=35
u3*5
u0
w
3
ext/2
2
1
0
-1
hier uA und u0 gleichphasig, aber uA
größer als u0. weil V = -32 (statt -29 )
-2
0
5
10
15
20
25
30
35
40
45
50
Bild 2: V= - 32, also zu groß, drum haben bei Selbsterregung (ab t = 35) uA und u0 ansteigende Amplitude
4
Bild=3,R1=1, C1=1, R2=1, C2=1, dt=0.01, R3=1, C3=1, V=-26, text=35
uA
u3*5
3
u0
w
uA
2
ext/2
u0
1
0
-1
hier uA und u0 gleichphasig, da aber v = -26 zu klein,
bei Selbsterregung abnehmende Amplituden uA und u3
-2
0
10
20
30
40
50
60
70
Bild 3: V= - 26, also zu klein, drum abnehmende Amplituden bei Selbsterregung ( ab t = 35)
4
Bild=4,R1=1, C1=1, R2=1, C2=1, dt=0.01, R3=1, C3=1, V=-100, text=35
uA
u3*5
3
u3 (trotz Begrenzung von uA
uA
u0
fast sinusförmig!)
w
ext/2
2
u0
1
0
-1
V = -100, also viel zu groß. Drum steigt uA bis in die Begrenzung, wird also
fast rechteckig! Trotzdem ist u3 noch nahezu sinusförmig!
-2
0
10
20
30
40
50
60
70
Bild 4: V = - 100, also viel zu groß ( V = -29 wäre richtig, s.o.) Drum geht uA bis in die Begrenzung (in
der Figur nicht sichtbar, weil Achsen in Y-Richtung begrenzt sind auf –2 bis 4 ). Trotz der Begrenzung
von uA ist die Spannung u3 nahezu sinusförmig. Das liegt daran, dass die Oberschwingungen von uA
(die infolge der Begrenzung entstehen) durch die Tiefpasswirkung der 3 RC-Glieder stark abgeschwächt
werden.
Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsytemtechnik,
A:\sinus\sinosz2.doc,
Seite 7/7
Anschließend die Matlab-Dateien,
mit denen das Simulink-Modell aufgerufen wird:
Es sind 4 „Parameter-Dateien“ SinOz10Parx.m mit Endziffer x = 1, 2, 3, 4. Diese Endziffer ist auch
gleichzeitig die Nummer des Bildes. Die Parameter-Datei ruft die (immer gleiche) „Stringdatei“
sinosz10str.m auf, die seinerseits die Simulink-Datei sinosz10.mdl aufruft und die Bilder zeichnet
und (mittels „Fadenkreuz“ ) die Parameterwerte in die Bilder schreibt.
So wird die Parameterdatei gestartet:
In Kommandoebene eintippen sinosz10parx ( mit x = 1,2,3,4, ohne Endung .m),
dann „Return“
Hier eine der Parameter-Dateien SinOz10Parx.m eingefügt,
anschließend die Stringdatei sinosz10str.m:
% Datei sinosz10par1.m Parameter-Datei für Sinosz10.MDL
clear;
format compact;
Bild=1;
R1=1;R2=1; R3=1; C1=1; C2=1; C3=1; max =10; min=-10;
V=-29;
dt=0.01;tmax=50;
wSt=1; wE=4; tex=35;
sinosz10str; % Aufruf Stringdatei sinosz110.m
%-------
% Datei Sinosz10Str.m; Stringdatei für Simulink sinosz10.MDL
if Bild ==1 sinosz10; end;%Aufruf der Schaltung sinosz10.MDL auf Bildschirm
S0=['Bild=', num2str(Bild)];
S1=[',R1=', num2str(R1)]; S2=[', C1=', num2str(C1)];
S3=[', R2=', num2str(R2)]; S4=[', C2=', num2str(C2)];S5=[', dt=',
num2str(dt)];
S6=[', R3=', num2str(R3)]; S7=[', C3=', num2str(C3)];
S8=[', V=', num2str(V)]; S9=[', text=', num2str(tex)];
[nix]=sim('sinosz10',[0,tmax]);% Starten von sinosz1.MDL
set(0,'DefaultLineLinewidth',1); % Linienstärke 1
figure(Bild); clf;
plot(t, uA, t, u3*5, t,u0, t,w, t,ext/2);
hold on;
%set(0,'DefaultLineLinewidth',1);
%plot(t,u1,t,u2);
grid;
axis([0,tmax,-2,4]);% Begrenzung x-Achse auf 0,tmax, y-Achse auf –2,4
gtext([S0,S1,S2,S3,S4,S5,S6,S7,S8,S9]); % Ausgabe Text-String auf Bild
legend('uA','u3*5','u0','w','ext/2');
hold off;