b : a = Steigung β = Neigung β

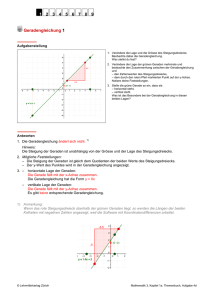
MathBuch 8+
Theorie
aufwärts — abwärts
LU 25
Bezirksschule Brugg
Steigung und Neigung
A
b : a = Steigung
c
b
= Neigung
B
C
a
Steigung:
Unter der Steigung versteht man den Quotienten von b : a.
Diesen Quotienten kann man als Bruch, als Dezimalbruch oder in % angeben.
Neigung:
Die Neigung wird mit Winkelgraden angegeben: gemeint ist der Winkel .
Beispiele:
In der obigen Zeichnung beträgt die Steigung:
In der obigen Zeichnung beträgt die Neigung:
Frage:
3 cm
8 cm
3
8
0,375 37,5%
21°
Welcher Neigungswinkel ergibt sich bei 100% Steigung?
Antwort: 45°
Es handelt sich um ein gleichschenklig-rechtwinkliges Dreieck:
100% = 1,0 = b : a
45°
b
b=a
b=a
b : a = 1,0 = 100%
90°
45°
a
Zusatz: für gewiefte Rechner
Steigung und Neigung können mit dem TR mit Hilfe der TAN-Funktion ineinander verwandelt
werden:
ARCTAN 0,375
20,56°
ARCTAN 1,0 = 45°
TAN 20,56°
0,375 = 37,5%
TAN 45° = 1 = 100%
ARCTAN und TAN:
ARCTAN (Arcustangens) ist die Umkehrfunktion von TAN (Tangens).
Auf einigen TR benützt man dazu entweder die 2nd-Taste und danach die TAN-Taste
oder die INV-Taste und danach die TAN-Taste.
1-2
MathBuch 8+
Theorie
aufwärts — abwärts
LU 25
Bezirksschule Brugg
Steigung und Neigung bei Geraden im Koordinatennetz
y = m•x
wobei m = Steigung der Geraden
y
3
x
5
Geraden durch den Nullpunkt nennt man Ursprungsgeraden.
Die Geradengleichung lautet: y = m•x
y = 0,6•x
m ist die Steigung der Geraden.
Geraden, die nicht durch den Nullpunkt gehen:
y = m•x + a
wobei m = Steigung der Geraden
a = Abschnitt auf der y-Achse
Steigung m:
m
3 1,5
4 1
1,5
3
1
2
Die Geradengleichung lautet: y = m•x + a
0,5
y = 0,5•x + 1
m ist die Steigung der Geraden, a ist der Abschnitt auf der y-Achse
2-2