mathematik-test 2007 - Bildungsplattform Bremerhaven
Werbung

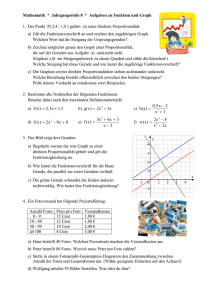
GYMNASIALE OBERSTUFEN UND FACHOBERSCHULEN DER STADT BREMERHAVEN 11. JAHRGANGSSTUFE MATHEMATIK-TEST 2007 Liebe Schülerinnen und Schüler, dieser Mathematik-Test dient der Selbsteinschätzung Ihrer mathematischen Kenntnisse und der Dokumentation Ihres Lernfortschritts. Ihren Lehrerinnen und Lehrern soll das Ergebnis dieses Tests wichtige Hinweise für die weitere Gestaltung des Unterrichts liefern. Schreiben Sie die Lösungen in die dazu vorbereitete Spalte oder kreuzen Sie die zutreffenden Antworten an. Für die Rechnungen und Nebenrechnungen verwenden Sie bitte den freien Platz. Machen Sie bitte folgende Angaben: Name: ................................................................ Vorname: ................................................................ Geschlecht: Name des jetzigen MAT-Lehrers: ................................................................ Jetzige Schule: ................................................................ Vorherige Schule: männlich weiblich / ...................................................... (Nummer siehe Rückseite) Vorherige Klasse: ..................................................... (genaue Bezeichnung) Vorherige Schulart: Gesamtschule Gymnasium Realschule sonstige Schule wie im Vorjahr Edith-Stein-Schule Gaußschule II Fachoberschule 222 851 174 Bearbeitungszeit: 80 Minuten Hilfsmittel: Lineal, kein Taschenrechner! Seite 2 von 6 Georg-Büchner-Schule II 456 Heinrich-Heine-Schule 551 Humboldtschule Immanuel-Kant-Schule 451 172 Johann-Gutenberg-Schule Körnerschule Lessingschule 458 455 454 Paula-Modersohn-Schule 457 Pestalozzischule II 453 Schule am Leher Markt 176 Wilhelm-Raabe-Schule 452 Schulen im Landkreis Wesermünde Sonstige Schule 111 999 Seite 1 von 6 1. Berechnen Sie: a) 2 1 5 5 3 7 b) 3 1 2 5 10 15 c) 3: Lösungen 1 2 2. Schreiben Sie die kleinere der beiden Zahlen in die Lösungsspalte: a) 7 ; 2 b) 8 17 ; 9 18 c) 7 ; 0, 07 10 3. Ersetzen Sie die drei Punkte durch das richtige Zeichen ( , ) und schreiben Sie dieses auch in die Lösungsspalte. 18 0,02 b) 0,3% Lösung 27 4. Schreiben Sie als Bruch: a) Lösungen 5. Lösungen Lösungen a) 100g einer Quarkspeise haben 300 Kalorien. Wie viele Kalorien haben dann 30g der selben Speise? b) Nach einer Preiserhöhung von 8% kostet ein Laptop 972,00 €. Wie viel € hat er vor der Preiserhöhung gekostet? c) Gib folgende Aussage in Prozent an: Jeder 5. europäische Straßentunnel fällt beim Sicherheitstest des ADAC durch. 6. Schreiben Sie den Term als Potenz von a mit der Form a n : Lösungen Seite 2 von 6 a) a 3 a 3 b) a3 a3 c) (a 3 ) 2 7. Schreiben Sie als Zehnerpotenz ( 10 x ): Lösungen zweihunderttausend 8. Schreiben Sie folgende Taschenrechneranzeige als Dezimalzahl: Lösung 6, 25 E 04 bzw. 6, 254 9. Vereinfachen Sie so weit wie möglich: a) a2 2abb2 a2 b2 b) 2( x22x1 ) (x1 )(x1 ) Lösungen 10. Lösen Sie die Gleichungen nach x auf: a) 4x 8 z b) x2 6 x 7 0 Lösungen 11. Telefoniert man mit einem Handy, so gibt es auch Tarife, bei denen man eine Grundgebühr zahlt und zusätzlich den Preis je telefonierter Minute. Der monatliche Gesamtpreis für die Handynutzung kann im mathematischen Sinn als lineare Funktion mit der allgemeinen Form f x mx b und einer Geraden als Graph aufgefasst werden. Welche der unteren Aussagen ist richtig/falsch? Kreuzen Sie an Richtig Falsch Die Grundgebühr liest man auf der x Achse ab. Die Grundgebühr stellt den Schnittpunkt mit der y Achse dar. Der Minutenpreis findet sich als Steigung wieder. Für b setzt man den Minutenpreis ein. f ( x ) ist die Grundgebühr. Der Faktor m gibt die Anzahl der telefonierten Minuten wieder. 12. Gegeben sind der Punkt P(2 /1) und die Steigung m bestimmen Sie die Gleichung der Geraden. 1 . Zeichnen Sie die Gerade und 4 Lösung Seite 3 von 6 13. Bestimmen Sie die Funktionsgleichungen der gezeichneten Graphen. g1 g2 14. Gegeben ist der Graph der Funktion 1 f(x) x21. 4 Allerdings fehlt die Beschriftung des Koordinatensystems. Beschriften Sie dieses. Lösungen Seite 4 von 6 y 15. Das Bild zeigt den Graphen einer Funktion: x Lösungen a) Welchen Wert hat die Funktion an der Stelle x 1 ? b) Bestimmen Sie den kleinsten dargestellten Funktionswert. c) Bestimmen Sie die Stelle(n), an der/denen die Funktion den Funktionswert 2 hat. 16. In welchem Punkt schneidet die Gerade mit der Funktionsgleichung g ( x) 2 x 5 die Gerade mit der Funktionsgleichung h( x) 2 x 3 Lösungen 17. Gegeben sind die Funktionsgleichungen zweier Geraden: g1 x 1 x 1 4 und g2 x 1 x 1 4 Welche der unteren Aussagen ist / sind korrekt? Kreuzen Sie an Richtig Falsch Die Geraden schneiden sich nie. Die Geraden besitzen denselben Schnittpunkt mit der y-Achse. Seite 5 von 6 Die Geraden sind orthogonal (senkrecht) zueinander. Die Geraden schneiden sich auf der x-Achse. Die Geraden haben dieselbe Steigung. 18. Bestimmen Sie a und b aus dem folgenden linearen Gleichungssystem: () a3b6 ()2ab2. Lösungen 19. Die allgemeine Form einer quadratischen Funktion kann f x ax2 b lauten. Als Beispiel ist hier der Graph von f x 3x2 4 gegeben. Kreuzen Sie an, welcher Koeffizient / welche Koeffizienten zu ändern ist/sind, um Lösungen a b a) die Parabel in y Richtung zu verschieben b) die Öffnung nach oben zu erreichen c) die Parabel breiter zu öffnen 20. Unter www.upi-institut.de/benzinpreise.htm ließ sich am 3. Mai 2007, 18:27 Uhr das folgende Diagramm für die Rohöl-Weltmarktpreise der Jahre 2004 bis 2006 herunterladen: Seite 6 von 6 Lösungen a) Wie viel Dollar kostete ein Barrel Rohöl Ende Mai 2006? b) Zu welchem Zeitpunkt war der Rohöl-Weltmarktpreis 2005 maximal? c) In welchen Monaten lag der Rohölpreis 2005 unterhalb der 50Dollar-Grenze? d) Um welchen Betrag ist der Rohölpreis von Ende Mai 2005 bis Ende März 2006 gestiegen?