Prüfungsaufgabe 2003

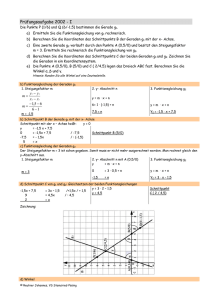
Prüfungsaufgabe 2003 - I
Gegeben sind drei Geraden:
Die Gerade g1 hat die Funktionsgleichung y1 = -
5
12
x + 4,5.
Die Gerade g2 verläuft durch die Punkte P (-3/-4) und Q (4,5/1).
Die Gerade g3 steht senkrecht zu g2 und schneidet die x- Achse im Punkt A (3/0).
g1 verläuft parallel zur x-Achse durch den Punkt A (-2|2),
a)
b)
c)
d)
e)
f)
Berechnen Sie die Funktionsgleichung der Geraden g2.
Geben Sie die Funktionsgleichung der Geraden g3 an.
Berechnen Sie den Schnittpunkt B der Geraden g1 und g2.
Zeichne Sie die drei Geraden in ein Koordinatensystem mit der Einheit 1 cm und beschriften Sie den
Schnittpunkt der Geraden g1 und g3 mit C.
Die Punkte A (3/0), B (6/2) und C (0/4,5) bestimmen das Dreieck ABC. Berechnen Sie den Umfang des
Dreiecks in cm.
Hinweis: Runden Sie die Seitenlängen auf eine Dezimalstelle.
Berechnen Sie die Winkel im Dreieck ABC
Hinweis: Runden Sie auf ganze Grad.
a) Funktionsgleichung der Geraden g2
1. Steigungsfaktor m
2. y- Abschnitt n
y2 − y2
m=
x 2 − x1
y=mwx+n
m=
-4=
m=
1 − (−4)
4,5 − (−3)
2
2
3
w (-3) + n
-2 = n
3
b) Funktionsgleichung der Geraden g3
Bei aufeinander senkrecht stehenden
Geraden gilt:
m1
w m2 = - 1
2
w m2 = - 1
3
m2 = -
3
2
y- Abschnitt
0=-
3
w3+n
2
n = 4,5
c) Schnittpunkt B von g1 und g2 : Gleichsetzen der beiden Funktionsgleichungen
2
5
2
x + 4,5
= w x -2
y = w 6 -2
12
3
3
13
y=2
x
= - 6,5
12
x
=6
d) Zeichnung
© Reutner Johannes, VS Stamsried-Pösing
3. Funktionsgleichung g2
y=m wx+n
Y2 =
2
3
w x -2
Funktionsgleichung g3
y3 = -
3
x + 4,5
2
Schnittpunkt
B ( 6/ 2)