Prüfungsaufgabe 1999 – I 3 2 1

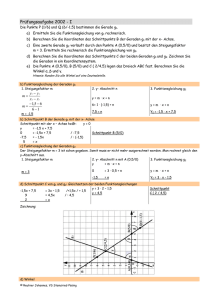
Prüfungsaufgabe 1999 – I
Die Punkte P1(-1,5/7,5) und P2(4,5/-2,5) bestimmen die Gerade g1. Eine weitere Gerade g2 mit der
Steigung m = 1 schneidet die x-Achse im Punkt A(-1/0).
a) Ermitteln Sie die Funktionsgleichungen beider Geraden rechnerisch und zeichnen Sie beide
Graphen in ein Koordinatensystem.
b) Berechnen Sie die Koordinaten des Schnittpunkts B der Geraden g1 mit der x-Achse.
c) Berechnen Sie die Koordinaten des Schnittpunkts C der beiden Geraden.
d) Durch eine zentrische Streckung mit Punkt C als Streckungszentrum wird das Dreieck ABC zum
Dreieck A'B'C vergrößert. Der Flächeninhalt des neuen Dreiecks soll neunmal so groß sein wie der
Flächeninhalt des Dreiecks ABC. Konstruieren Sie das Bilddreieck A'B'C.
a) Funktionsgleichung der Geraden g1
1. Steigungsfaktor m
y2 − y2
x 2 − x1
− 2,5 − 7,5
m=
4,5 − (−1,5)
2. y- Abschnitt n
3. Funktionsgleichung
m=
m=-
1
y=mwx+n
-2,5 = -
2
3
1
2
w 4,5 + n
3
5=n
a) Funktionsgleichung der Geraden g2
1. Steigungsfaktor m
m=1
2. y- Abschnitt n
y=mwx+n
0 = 1 w (-1) + n
1=n
y=m wx+n
Y=-
1
2
w x +5
3
3. Funktionsgleichung
y=m wx+n
Y = x +1
b) Schnittpunkt B von g1 mit der x- Achse
Lösungsschema: y = 0
0
-5
2
w x +5
3
2
=-1 wx
3
=-
1
/ : (5)
Antwort: der Schnittpunkt mit der x- Achse hat die
Koordinaten B ( 3 / 0 )
3
=x
b) Schnittpunkt C beider Geraden ( = Gleichsetzen der Funktionsgleichungen)
Einsetzen in eine Funktionsgleichung:
2
- 1 w x +5
= x +1
3
Y = 1,5 +1
x
= 1,5
Y = 2,5
Schnittpunkt C ( 1,5 / 2,5)
d) Zentrische Streckung
Streckungsfaktor bei Strecken ist k2; k2 = 9 , d.h. k = 3
© Reutner Johannes, VS Stamsried-Pösing