Übungsblatt 3

Computergrafik
Sommersemester 2004
Übungen
Peter Dannenmann
Blatt 3
Abgabe: 1.7.2004
Aufgabe 1: Szenenerstellung in VRML
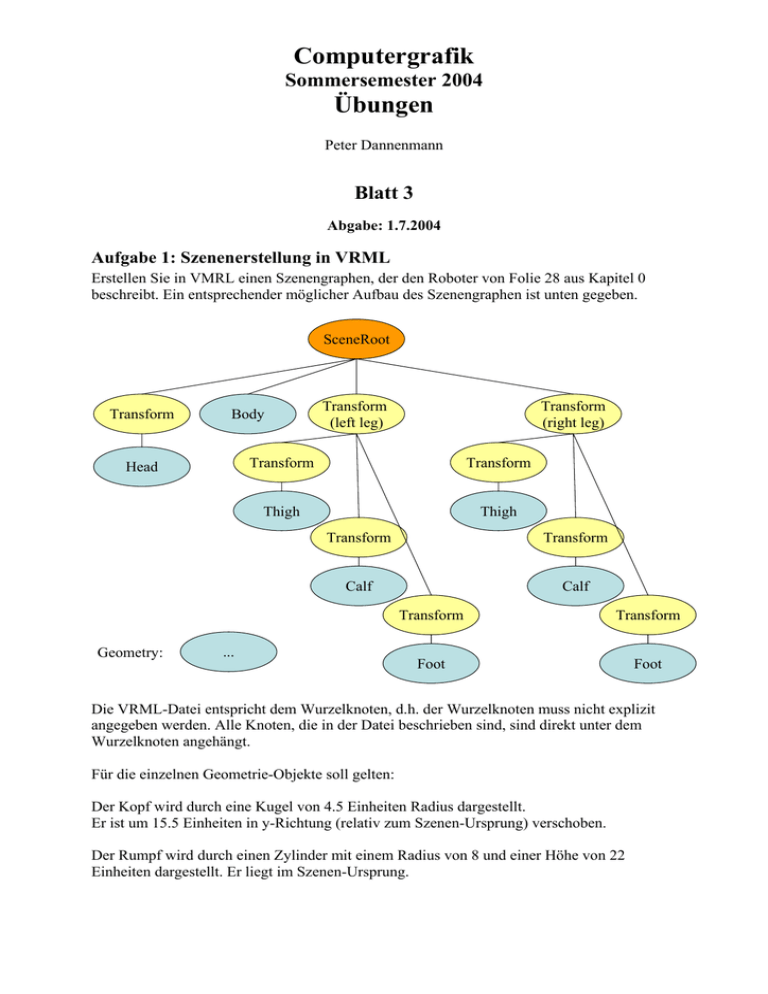
Erstellen Sie in VMRL einen Szenengraphen, der den Roboter von Folie 28 aus Kapitel 0
beschreibt. Ein entsprechender möglicher Aufbau des Szenengraphen ist unten gegeben.
SceneRoot
Transform
Body
Head
Geometry:
Transform
(left leg)
Transform
(right leg)
Transform
Transform
Thigh
Thigh
Transform
Transform
Calf
Calf
...
Transform
Transform
Foot
Foot
Die VRML-Datei entspricht dem Wurzelknoten, d.h. der Wurzelknoten muss nicht explizit
angegeben werden. Alle Knoten, die in der Datei beschrieben sind, sind direkt unter dem
Wurzelknoten angehängt.
Für die einzelnen Geometrie-Objekte soll gelten:
Der Kopf wird durch eine Kugel von 4.5 Einheiten Radius dargestellt.
Er ist um 15.5 Einheiten in y-Richtung (relativ zum Szenen-Ursprung) verschoben.
Der Rumpf wird durch einen Zylinder mit einem Radius von 8 und einer Höhe von 22
Einheiten dargestellt. Er liegt im Szenen-Ursprung.
Computergrafik
Sommersemester 2004
Übungen
Peter Dannenmann
Das linke Bein ist um (5; -11; 0) Einheiten relativ zum Szenen-Ursprung verschoben, das
rechte Bein um (-5; -11; 0) Einheiten.
In jedem Bein ist der Oberschenkel um -6 Einheiten in y-Richtung (relativ zum Ursprung des
Beines, der durch oben beschriebene Translation gegeben ist) verschoben. Zusätzlich ist das
lokale Koordinatensystem des Oberschenkels um -90 Grad um die z-Achse gedreht.
Der Oberschenkel wird durch einen Quader der Ausdehnung (12; 3.5; 3.5) dargestellt.
Analog ist der Unterschenkel um -18 Einheiten in y-Richtung verschoben und sein lokales
Koordinatensystem ist ebenso gedreht wie das des Oberschenkels. Der Unterschenkel wird
durch einen Quader der Ausdehnung (12; 3; 3) dargestellt.
Der Fuß schließlich ist um (0; -25.5; 1.5) relativ zum Ursprung des Beins verschoben und sein
lokales Koordinatensystem ist um 90 Grad um die y-Achse gedreht. Der Fuß wird durch einen
Quader der Ausdehnung (6; 3; 3) dargestellt.
Alle Transformationen der Geometrien beziehen sich auf deren Mittelpunkt, der gleichzeitig
Ursprung deren lokalen Koordinatensystems ist.
Die Gruppierung mehrerer Knoten unter einem Transform-Knoten kann in VRML
folgendermaßen realisiert werden:
#VRML V2.0 utf8
# Einzelner Knoten, der direkt unter der Wurzel hängt, ohne Transformation
Shape {
appearance Appearance {
material Material { }
}
geometry Cylinder { }
}
# Einzelner Knoten, der direkt unter der Wurzel hängt, mit Transformation
Transform {
translation 0 15.5 0
children [
Shape {
appearance Appearance {
material Material {
diffuseColor 0.3922 0.2431 0.1647
ambientIntensity 1.0
specularColor 0 0 0
shininess 0.145
transparency 0
}
}
geometry Sphere {
radius 4.5
}
}
]
}
Computergrafik
Sommersemester 2004
Übungen
Peter Dannenmann
# Mehrere Kinder unter einem Transformationsknoten
Transform {
translation 0 15.5 0
children [
Transform {
translation 0 -6 0
rotation 0.0 0 1.0 -1.571
children [
Shape {
appearance Appearance {
material Material {
...
}
}
geometry Sphere {
radius 4.5
}
}
]
}
Transform {
translation 0 6 7.7
rotation 0.0 0 1.0 -1.571
children [
Shape {
appearance Appearance {
material Material {
...
}
}
geometry Sphere {
radius 4.5
}
}
]
}
]
}
Aufgabe 2: Laden von VRML-Dateien in Java3D
Auf der Web-Seite finden Sie ein Beispielprogramm, das VRML-Dateien in Java3D lädt.
Compilieren Sie das Programm und laden Sie die Beispiel-Szenen, die Sie ebenfalls auf der
Web-Seite finden.
Adaptieren Sie anschließend das Programm so, dass das Navigationssystem (mittels
MouseBehaviors) nicht wie in dem gegebenen Beispiel die Szene sondern den Viewpoint
transformiert.