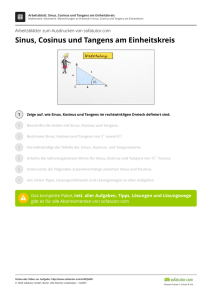
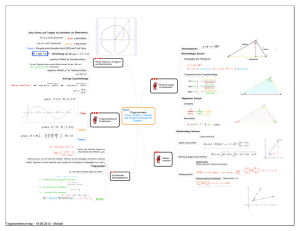
Konstruktion der Winkelfunktionen im 1. Quadranten des

GF MA
Trigonometrie
A2
Konstruktion der Winkelfunktionen im 1. Quadranten des Einheitskreises1
Wie der Name vermuten lässt, ist der Einheitskreis ein Kreis, dessen Radius genau „eine Einheit“ lang
ist, und diese Eigenschaft macht es möglich die Werte der trigonometrischen Funktionen von
beliebigen Werten grafisch darzustellen.
Folgend ein Einheitskreis. Der Kreis erstreckt sich über alle vier Abschnitte des Koordinatensystems,
genannt „Quadranten“.
Sinus und Cosinus
Wir zeichnen ein rechtwinkliges Dreieck, wie unten abgebildet, in den ersten Quadranten ein.
Da der Kreis den Radius 1 hat, ist die Hypotenuse des blauen Dreiecks ebenfalls nur eine Einheit lang
und es folgt:
sin (ϕ ) =
Gegenkathete Gegenkathete
=
= Gegenkathete
Hypotenuse
1
cos (ϕ ) =
Ankathete
Ankathete
=
= Ankathete
Hypotenuse
1
1
Dieses Arbeitsblatt basiert auf http://www.mathe-online.at/lernpfade/einheitskreis/?kapitel=2
1/4
GF MA
Trigonometrie
A2
Damit können wir die folgende Skizze erstellen:
Tangens
Nun ist ein Dreieck gesucht dessen Ankathete gleich 1 ist, damit, ähnlich wie bei Sinus und Cosinus,
wieder gilt:
tan (ϕ ) =
Gegenkathete Gegenkathete
=
= Gegenkathete
Ankathete
1
Der tan (ϕ ) entspricht demnach der Gegenkathete dieses Dreiecks und du kannst seinen Wert
bestimmen, indem du die Länge der Gegenkathete abmisst.
2/4
GF MA
Trigonometrie
Wir fassen zusammen:
•
Der Sinus wird auf der Katheten senkrecht zur x -Achse abgelesen, entspricht also der
y -Koordinate von P .
•
Der Cosinus wird auf der Katheten auf der x -Achse abgelesen, entspricht also der
x -Koordinate von P .
•
Der Tangens wird auf der Tangenten abgelesen, die im Punkt (1 / 0 ) den Einheitskreis
berührt.
Aufgabe 1:
Welche Werte können der Sinus, der Cosinus und Tangens im 1. Quadranten des
Einheitskreises annehmen?
Aufgabe 2:
Bewege nun den Punkt P auf dem Einheitskreis. Es soll weiterhin gelten, dass der
Sinus der y-Koordinaten und der Cosinus der x-Koordinaten des Punktes P
entspricht. Auch der Tangens wird weiterhin auf der Tangenten abgelesen, die im
Punkt (1 / 0 ) den Einheitskreis berührt.
a)
Welche Werte können der Sinus, der Cosinus und Tangens im 2. Quadranten
des Einheitskreises annehmen?
3/4
A2
GF MA
Trigonometrie
b)
A2
Welche Werte können der Sinus, der Cosinus und Tangens im 3. Quadranten
des Einheitskreises annehmen?
c)
Welche Werte können der Sinus, der Cosinus und Tangens im 4. Quadranten
des Einheitskreises annehmen?
Aufgabe 3:
Wir ergänzen gemeinsam die Tabelle zu den Quadrantenrelationen.
Winkel α
0°
Quadrant
x
90°
I
y
180°
II
x(-)
270°
III
360°
y(-)
IV
x
sin (α)
cos ( α )
tan ( α )
Aufgabe 4:
Aufgabe 5:
Zeige, dass für 0° ≤ α < 360° gilt
a)
(sin (α )) + ( cos (α ))
b)
tan (α ) =
2
2
=1
sin (α )
cos (α )
In den folgenden beiden Skizzen hat sich jeweils ein Fehler eingeschlichen. Kannst du
ihn finden?
4/4