Kreisbewegung
Werbung

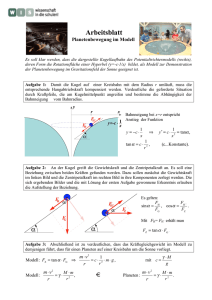
Die Kreisbewegung ================================================================== 1. Beschreibung der Kreisbewegung -----------------------------------------------------------------------------------------------------------------y v(t) ϕ(t) r(t) ϕ(t) x r Die Bewegung eines Körpers auf einer Kreisbahn vom Radius r kann beschrieben werden durch x(t) a) seinen Ortvektor r(t) = y(t) b) durch den Winkel ϕ(t) den der Ortvektor r(t) mit der positiven x-Achse bildet. Der Winkel ϕ(t) wird im Bogenmaß gemessen d. h. ist s der Bogen den der Winkel aus dem Kreis ausschneidet, dann ist ϕ = s r Eine Keisbewegung heißt gleichförmig, wenn vom Ortsvektor in der Zeit ∆t überstrichene Winkel ∆ϕ proportional zu ∆t ist. Der konstante Quotient ω = ∆ϕ ∆t gibt dann an, welcher Winkel pro Sekunde überstrichen wird und heißt deshalb Winkelgeschwindigkeit ω der Kreisbewegung. Ist T die Umlaufsdauer d.h die Zeit die der Körper für eine Umdrehung benötigt, dann gilt ω = 2π π T Befindet sich der Körper zur Zeit t = 0 auf der positiven x-Achse des Koordinatensystems d. h., ϕ(0s) = 0, dann schließt der Ortsvektor zur Zeit t den Winkel ϕ(t) = ω⋅t Ist ϕ(0s) = ϕ0, dann ist ϕ(t) = ω⋅t + ϕ0 Beachte : ω = 1(rad) = s−1 mit 1 rad = 1 ⋅180° s π Technisch beschreibt man gleichförmige Kreisbewegungen durch Angabe der Frequenz f. Sie gibt an, wie viele Umdrehungen der Körper pro Sekunde ausführt. Es ist daher 1 und ω = 2π π⋅f T -----------------------------------------------------------------------------------------------------------------Folgerungen : f = a) Für den Ortsvektor einer gleichförmigen Kreisbewegung mit ϕ(0s) = 0 gilt r⋅⋅cosϕ ϕ(t) r⋅⋅cos(ω ωt) r(t) = = r(t) = r⋅⋅sinϕ r⋅⋅sin(ω ϕ(t) ωt) b) In der Zeit T legt der Körper den Umfang U des Kreises zurück. Also gilt für die Bahnge schwindigkeit v v = 2π π⋅r = ω⋅r = const. T d.h., die gleichförmige Kreisbewegung ist eine Bewegung bei der sich Richtung der Geschwindigkeit, nicht jedoch ihr Betrag ändert. Für den Geschwindigkeitsvektor gilt dann − ωr⋅⋅sinϕ ϕ(t) − ωr⋅⋅sin(ω ωt) v(t) = = ωr⋅⋅cos(t) ωr⋅⋅cos(ω ωt) ___________________________________________________________________________ 2. Die Zentripetalkraft -----------------------------------------------------------------------------------------------------------------Damit sich ein Körper auf einer Kreisbahn bewegt, muss in jedem Punkt der Bahn eine konstante Kraft zum Kreismittelpunkt hin wirken. Diese Kraft heißt Zentripetalkraft Fr und die von ihr hervorgerufene Beschleunigung Zentripetalbeschleunigung ar . Ergebnis : Bewegt sich ein Körper mit der Bahngeschwindigkeit v bzw. der Winkelgeschwindigkeit ω auf einer Kreisbahn vom Radius r, dann muss er zum Mittelpunkt der Kreisbahn hin beschleunigt werden. Für den Betrag der Zentripetalbeschleunigung gilt ar = v2 = ω2r r Die diese Beschleunigung notwendige Zentripetalkraft ist ebenfalls zum Mittelpunkt hin gerichtet und hat den Betrag Fr = m v2 = mω ω2r r Anwendungen ================================================================== 1. Looping G FB FB G Ein 300 kg schwerer Wagen Wagen fährt mit v = 90 km in einen kreisförmigen Looping h vom Radius r = 10 m. a) Mit welcher Kraft drückt der Wagen im Punkt A gegen den Boden? a) Berechne die Geschwindigkeit des Wagens im höchsten Punkt A der Bahn. b) Wie groß ist die Kraft, mit der der Wagen in A gegen die Schienen gedrückT wird? a) FA − G = Fr ⇒ FA = Fr + G 2 FA = m⋅g + m⋅ b) 625 2 v v = m⋅(g + ) r r FA = 300 kg ⋅ (9,81 1 1 m⋅vA2 = m⋅vB2 + mg⋅2r ⇒ 2 2 vA = 625 c) FB + G = Fr ⇒ m + ) = 21,7 kN 10 m s2 ⋅vA2 − 4g⋅r vB = m2 m m − 4⋅9,81 2 ⋅ 10 m = 15,3 2 s s s ⇒ Fb = Fr − G v2 v2 FB = m⋅ − m⋅g = m⋅( − g) r r d) FB = 0 m2 s2 m⋅ m (15,3 s )2 m Fb = 300 kg ⋅ − 9,81 2 = 4,1 kN s 10 m vB2 = mg ⇒ vB = r g⋅r vB = 9,81 m m ⋅ 10 m = 9,9 2 s s m 2 m m km ) + 4 ⋅ 9,81 2 ⋅ 10 m = 22,1 = 80 s s h s -----------------------------------------------------------------------------------------------------------------2. Kugel in der rotierenden Halbkreisrinne vA = vB2 + 4g⋅r vA = (9,9 M α F α Fr m G Die auf die Kugel wirkende Gewichtskraft G und die von der Bahn stammende Kraft F ergeben die Zentripetalkraft. Fr m⋅ω2⋅r ω2⋅R⋅sinα Es gilt dann tanα = = = G g m⋅g ⇒ cosα = g g = 2 R⋅ω R⋅4π2⋅f2 R = 1m f (Hz) α 1 75° 2 86° 3 88° 5 89° 10 89,9° -----------------------------------------------------------------------------------------------------------------3. Das konische Pendel - Kettenkarussel Die auf die Kugel wirkende Gewichtskraft G und die vom Faden stammende Zugkraft F ergeben die Zentripetalkraft. Fr m⋅ω2⋅r ω2⋅L⋅sinα tanα = = = G g m⋅g ⇒ g g cosα = = 2 L⋅ω R⋅4π2⋅f2 α L α F m Fr G -----------------------------------------------------------------------------------------------------------------4. Rotierende Füssigkeitsoberfläche Für ein Teilchen im Abstand r von der Drehachse ergibt sich aus dem Kräftedreieck tanα = Fr m⋅ω2⋅r ω2⋅r = = G g m⋅g Ist die Oberflächenkurve der Graph der Funktion f : r → f(r) gegeben durch dann ist tanα = ω2⋅r = f '(r) g m⋅ω2 r2 ⋅ + C d.h. die Flüssigkeitsoberfläche ist ein Paraboloid. m⋅g 2 -----------------------------------------------------------------------------------------------------------------5. Kurvenfahrt eines Pkw ohne Straßenüberhöhung Damit gilt f(r) = Damit die Kurve sicher durchfahren eerden kann muss gelten Fr ≤ FR = µH⋅m⋅g mit dem Haftreibungskoeffizienten µH -----------------------------------------------------------------------------------------------------------------5. Neigung eines Zweirads in der Kurve α F Fr G α − Fr − F G Um ein Kippen zu vermeiden muss sich ein Zweiradfahrer in Kurve neigen. Die Gewichtskraft G und die vom Boden stammende Kraft F ergeben die Zentripetalkraft. Die Zentripetalkraft darf wieder nicht größer als die Haftreibungskraft sein. 2 m⋅ vr m⋅v2 = Es ist tanα = g g⋅r -----------------------------------------------------------------------------------------------------------------6. Kurvenfahrt eines PKW mit Straßenüberhöhung FB G Fr 2 m⋅ vr Fr v2 Es gilt tanα = = = G m⋅g g⋅r ___________________________________________________________________________ 4. Rotierende Füssigkeitsoberfläche Für ein Teilchen im Abstand r von der Drehachse ergibt sich aus dem Kräftedreieck tanα = Fr m⋅ω2⋅r ω2⋅r = = G g m⋅g Ist die Oberflächenkurve der Graph der Funktion f : r → f(r) gegeben durch dann ist tanα = ω2⋅r = f '(r) g m⋅ω2 r2 ⋅ + C d.h. die Flüssigkeitsoberfläche ist ein Paraboloid. m⋅g 2 ___________________________________________________________________________ Damit gilt f(r) =