Neuroinformatik II Theorie neuronaler Netze

Neuroinformatik II
Theorie neuronaler Netze
Günther Palm und Friedhelm Schwenker
Institut für Neuroinformatik
• Vorlesung (3h) Übungen (1h): Di 12.00-13.30 und Fr 10.15-11.45 Uhr H21 (1.Übung: 7.5.)
Schein: 50% der Punkte (6 übungsblätter) + aktive Übungsteilnahme; Bonusregel gilt!
• Kernfächer/-module: Mathematische und theoretische Methoden der Informatik, Praktische Informatik
• Vertiefungsfach/-module: Neuroinformatik, Mustererkennung
• Projektmodul: Neuroinformatik
Inhalt der Vorlesung
1. Modellierung neuronaler Netze
2. Stabilität in Neuronalen Netzen
3. Lernen in Einschichtnetzen: Perzeptron, Assoziativspeicher, Pseudoinverse, Supportvektor-Lernen, PCA
4. Lernen in Mehrschichtnetzen: MLP, RBF-Interpolation, nichtlineare SVM
5. Darstellung mit NN: Satz von Cover, Satz von Cybenko bzw. Hornik
6. Komplexität der Netze und des Lernens: neuronale Schaltungen, NPVollständigkeit
7. Robustheit, Generalisierung und Bias-Varianz-Zerlegung
1. Modellierung neuronaler Netze
1. Biologische Grundlagen
2. Allgemeines Kanalmodell
3. Vereinfachte Neuronenmodelle
4. Quasi-stationäre Lösungen
1.1 Biologische Grundlagen
Der Kortex des menschlichen Gehirns mit verschiedenen Arealen.
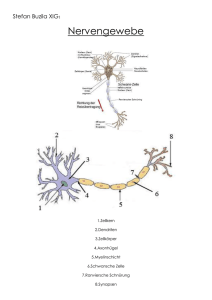
Die Hauptbestandteile eines typischen Neurons sind:
• Dendriten bzw. Dendritenbaum
• Zellkörper (Soma)
• Nervenfaser (Axon) mit dem axonalen Baum
Dendriten(baum)
Axonhügel
axonale
Endknöpfchen
mit Synapsen
Zellkörper mit
Zellkern
Axon
Synapse mit der prä- und postsynaptischen Membran.
Ausschüttung der Neurotransmittermoleküle in den synaptischen Spalt.
ankommendes
Aktionspotential
Axonendigung
Vesikel mit
Transmittermolekülen
Transmittermolekül
präsynaptische
Membran
postsynaptische Membran mit Rezeptoren für die Transmittermoleküle
Zellmembran - offene und verschließbare Ionenkanäle sind abgebildet.
offener Kanal
Ionen
geschlossener
Kanal
Außenseite der Zellmembran
Zellmembran
Innenseite der Zellmembran
Typische Ionenkonzentrationen (für (Tintenfisch-)Axon in Millimol/Liter)
Typ
innen
außen
K+
400
20
Cl−
30
590
N a+
60
436
Aktionspotential
mV
4
+40
t
0
5
3
-60
-70
1
1
Na+
außen
Membran
innen
K+
außen
Membran
innen
2
6
7
Schwelle
Ruhepotential
2
3
4
5
6
7
Räumlich/zeitliche Summation auf dem Dendritenbaum
3
hemmende Synapse
4
0
1
erregende Synapsen
2
räumliche Summation
mV
Schwelle
-60
EPSP
Ruhepotential
Zeit
IPSP
-70
1
0
0+1
2
3
4
1+2
1+2+3
(jeweils Nummern der Synapsen)
zeitliche Summation
mV
-60
-70
(nur eine Synapse z. B. Nr. 1 beteiligt)
Schwelle
Ruhepotential
Zeit
Zeitpunkte der Spikes
Dynamik der neuronalen Verarbeitung
• Summation am Zellkörper EPSP/IPSP von vorgeschalteten Neuronen
führen zu Potentialveränderungen am Dendritenbaum/Zellkörper ( räumlich/zeitliche Summation der EPSP/IPSP)
• Auslösung eines Aktionspotentials Ändert sich das Membranpotential
am Zellkörper nur schwach, wird kein Aktionspotential ausgelöst (unterschwelligen Erregung). Bei hinreichend starker Depolarisation der Membran wird im Bereich des Axonhügels ein Aktionspotential ausgelöst.
• Ausbreitung des Aktionspotentials Das Aktionspotential breitet über
das Axon bis in den axonalen Baum mit konstanter Amplitude aus
• Synaptische Übertragung Das Aktionspotential führt in den axonalen
Endknöpfchen zu einer Ausschüttung von Neurotransmittern, die auf der
postsynaptischen Membran zu einer Änderung des Membranpotentials
führen.
Computer
Neuronale Netze
kaum fehlertolerant
fehlertolerant, robust gegenüber
verrauschten oder widersprüchlichen Daten
Hardwarestörungen bzw. -ausfall
führen zum Totalausfall des Gesamtsystems
Störung an einzelnen Neuronen
oder der Ausfall von Neuronen bedeutet kein Totalausfall, das Gesamtsystem funktioniert mit eingeschränkter Funktionalität weiter
explizite Programmierung
Lernen durch Beispiele
wenige, aber komplexe Prozessoren (typischerweise 100)
sehr viele einfache Neuronen (im
menschlichen Gehirn ca. 1011)
niedriger Vernetzungsgrad (Verbindungen ∼ 102 am Prozessor)
hoher Vernetzungsgrad (bis zu 104
Synapsen pro Neuron)
Schaltzeiten der Prozessoren sind
kurz (heute im 108 Hz-Bereich)
Schalt– und Laufzeiten der Neuronen sind lang (im 102 Hz-Bereich)
1.2 Allgemeines Kanalmodell
Modellvoraussetzungen:
• I = {1, . . . , N } die Menge der Neuronen.
• Jedes Neuron j ist von einem bestimmten (Membran-)Typ l und einem
bestimmten (Übertragungs-)Kanaltyp k.
• τl > 0 Zeitkonstante und ϑl : R+ → R+ die Schwellenfunktion für den
Membrantyp l.
• rk : R+ → R+ die Responsefunktion und Uk Umkehrpotentiale für den
Übertragungskanaltyp k.
• C = (cij ) synaptische Kopplungsmatrix und D = (dij ) Matrix der Delays.
Neuronenmodelle
(1) Dendritisches Potential uj des Neurons j vom Membrantyp l
τl u̇j (t) = −uj (t) +
X
akj (t)(Uk − uj (t)) + xj (t)
k
(V) Variante: uj wird nach Spike von j auf Ruhepotential U0 gesetzt.
(2) Gesamtinputaktivität akj im Übertragungskanal k des Neurons j
akj (t)
=
X
aij (t)
Ik Neuronen vom Kanaltyp k
i∈Ik
Übertragene Aktivität aij vom Neuron i zum Neuron j im Kanal k
aij (t) =
X
s∈Tti
rk (t − (s + dij ))cij =
X
s<t
rk (t − (s + dij ))yi(s)cij
(3) Outputaktivität yj des Neurons j
yj (t) = 1[uj (t)≥θj (t)]
(4) Schwellenfunktion θj und Spikezeitpunkte Ttj von Neuron j (vom Membrantyp l)
Ttj = {s < t | yj (s) = 1}
θj (t) = max ϑl(t − s)
j
s∈Tt
(5) Diskretisierung von (1) mit ̺l :=
∆t
τl
und ̺l ∈ (0, 1]
uj (t + ∆t) = (1 − ̺l) · uj (t) + ̺l
X
k
akj (Uk − uj (t)) + ̺lxj (t)
Vereinfachungen
a) Response Funktion durch Gesamtwirkung wij beschreiben:
′
(2 )
akj (t)
=
X
wij yi (t − dij )
i∈Ik
b) Uk − u ersetzen durch Uk (unterhalb der Schwelle ist u klein):
′
(1 )
τlu̇j (t) = −uj (t) +
X
akj (t)Uk + xj (t)
k
Mit (2′) folgt:
′′
(1 )
τl u̇j (t) = −uj (t) +
X
wij yi(t − dij ) + xj (t)
i
c) Einfache zweiwertige Schwellenfunktion ϑ(t) ∈ {ϑref , ϑrest}.
d) Schwellenmechanismus (mit ϑl ) durch Ratenfunktion fl ersetzen:
(3′)
e) Alle Delays = 1; alle Delays = 0.
yj (t) = fl (uj (t))
1.3 Vereinfachte Neuronenmodelle
Kanalmodell: Gleichungen 1, 2, 3 und 4
Spike-Response-Modell: 1′, 2, 3 und 4
Dynamic-Threshold-Modell: 1, 2′, 3 und 4
Integrate-and-Fire-Modell: 1′′ mit Variante (V), 3, 4 und mit einfacher
Schwelle (d)
Ratenmodell: 1, 2 und 3′
Grundmodell: 1′′ und 3′
Lineares Modell: 1′, 3′ und mit linearer Ratenfunktion f
Einfaches lineares Modell: 1′′, 3′, Delays alle = 0 und mit linearer Ratenfunktion f
1.4 Quasi-stationäre Lösungen
1. Ratenfunktion fl(u) aus Schwellenfunktion ϑl(t) bestimmen.
yj = fl (uj ) =
2. Gesamtwirkung r̂k :=
R
1
ϑ−1
l (uj )
für j vom Membrantyp l
rk (t)dt aus der Responsefunktion rk (t).
Diese beiden Vereinfachungen ergeben das Grundmodell mit:
akj
=
X
r̂k yi cij =
i∈Ik
li Membrantyp des Neurons i.
X
i∈Ik
r̂k fli (ui) cij
3. Berechnung der Fixpunkte mit dem Ansatz 0 ≈ u̇j
0 ≈ τk u̇j = −uj +
X
akj (Uk − uj ) + xj
⇐⇒
uj ≈
xj +
k
P
1+
k
k aj Uk
P k
k aj
4. Linearisierung ergibt ein homogenes einfaches lineares Modell
DGL des dendritischen Potentials lautet mit den Vereinfachungen:
X
X
(Uk − uj )r̂k
τl u̇j = −uj +
fli (ui )cij + xj
(1)
i∈Ik
k
Betrachten nun DGL für uj = uj + ej :
X
X
τl (u̇j + ėj ) = −(uj + ej ) +
(Uk − (uj + ej ))r̂k
fli (ui + ei )cij + xj
(2)
i∈Ik
k
Nun setzen wir ein fli (ui + ei ) ≈ fli (ui ) + ei fl′ (ui )
i
X
X
τl (u̇j + ėj ) = −(uj + ej ) + xj +
(Uk − (uj + ej ))r̂k
(fli (ui ) + ei fl′ (ui ))cij
i
k
i∈Ik
τl (u̇j + ėj )
=
X
X
−(uj + ej ) + xj +
(Uk − uj )r̂k
fli (ui )cij
i∈Ik
k
+
X
(Uk − uj )r̂k
−
k
ei fl′ (ui )cij
i
i∈Ik
k
X
X
ej r̂k
X
fli (ui )cij −
i∈Ik
X
ej r̂k
X
ei fl′ (ui )cij
i
i∈Ik
k
P
P
Die Summanden k r̂k i∈I ej ei fl′ (ui )cij sind quadratisch in den Störungstermen ej
i
k
und können bei der Linearisierung vernachlässigt werden:
X
X X
X
′
r̂k
fli (ui )cij
τl ėj = −ej +
(Uk − uj )r̂k
ei fl (ui )cij − ej
i
k
i∈Ik
k
i∈Ik
Mit C̄ij = r̂k fli (ui )cij und Ĉij = (Uk − uj )r̂k fl′ (ui )cij folgt die lineare DGL:
i
τl ėj = −ej − ej
XX
k
i∈Ik
C̄ij +
XX
k
i∈Ik
Ĉij ei
Insgesamt erhält man ein homogenes lineares System von DGl 1. Ordnung der Form
ė = Ae
mit e = (e1, . . . en)T , ė = (ė1, . . . ėn)T und mit der reellen n × n Matrix
A = (aij ) definiert durch
ajj
XX
1
= − (1 +
C̄ij )
τl
k i∈Ik
und
1 XX
aji =
Ĉij ,
τl
k i∈Ik
Stabilität dieses Systems ist zu untersuchen.
Wir betrachten dafür einfache lineare neuronale Netze.
i 6= j