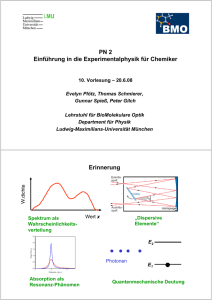
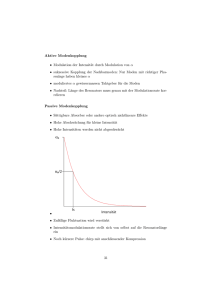
Physik PHB3/4 (Schwingungen, Wellen, Optik) Seite 2 Optische
Werbung

Physik PHB3/4 (Schwingungen, Wellen, Optik) Seite 04_GeomOptikAbbildung1_BA.doc - 1/5 2 Optische Abbildungen Abbildung im mathematischen Sinn: Von einem Gegenstandspunkt ausgehende Strahlen werden in einem Bildpunkt vereinigt. Ideale optische Abbildungen sollten noch weitere Forderungen erfüllen: Eine Gerade geht wieder in einen Gerade über (Kolineation) Die Abbildung ist maßstabsgetreu Reale Abbildungen sind nicht mehr streng punktförmige Abbildungen, sie sind nicht immer kolinear und maßstabsgetreu. Im obigen Sinn ist nur die Abbildung am ebenen Spiegel ideal. Die gebräuchlichsten Abbildungssysteme sind Spiegel und Linsen. Neuere Methoden: Diffraktive Optik, z.B. mit holographischen Linsen. 2.1 Vorzeichenkonvention in der Technischen Optik (DIN 1335) Bezeichnungen: Punkte: latein. Großbuchstaben (O, F, S ....) Strecken: latein. Kleinbuchstaben (a,s,f ....) Winkel: griech. Kleinbuchstaben (, , ...) Strecken und Winkel sind gerichtete Größen. konjugierte Größen1: ABBILDUNG Gegenstand (Objekt) Gegenstandsraum a, z (Objekt-) y n H s nicht konjugierte Größen2: F f (Objekt-) Bild Bildraum Strecken Größen Brechzahlen Hauptpunkte bzw. Hauptebenen Schnittweiten (Bild-) a', z' y' n' H' Brennpunkte Brennweite (Bild-) F' f' s' Achsensystem: Die Symmetrieachse ist die optische Achse (z-Achse von links nach rechts). Die y-Achse steht senkrecht auf der z-Achse und weist von unten nach oben. Strecken, die von einem Bezugspunkt nach rechts gemessen werden, sind positiv (in Lichtrichtung). Strecken, die nach links gemessen werden, sind negativ Strecken, die nach oben gemessen werden, sind positiv (pos. y-Richtung) Stecken, die nach unten gemessen werden, sind negativ. Winkel, dessen Fahrstrahlen durch Drehung in mathematisch positiven Sinn mit der optischen Achse zur Deckung gebracht werden, sind positiv. Lichtrichtung: Licht läuft in Richtung der pos. z-Richtung von links nach rechts. 1 Größen, die ineinander "abgebildet" werden. 2 Größen, die auch paarweise auftreten, aber nicht ineinander abgebildet werden. Physik PHB3/4 (Schwingungen, Wellen, Optik) Seite 04_GeomOptikAbbildung1_BA.doc - 2/5 Beispiel: Bezugspunkt des Koordinatensystems in H (Gegenstandsraum) bzw. H' (Bildraum) L i c h tri c h t u n g O b je k t ra u m B i ld ra u m (-)r 2 y y _ F S1 H _ (-)f (-) z F' S2 H' z' z O (+ )r 1 y' O' o p t. A c h s e y' (+ )f ' (-)a (+ ) z ' (+ )a ' a , a ' h a u p t p u n k tb e z o g e n z , z ' b r e n n p u n k tb e z o g e n S , S h e iß e n F l ä c h e n s c h e ite l 1 2 2.2 Bildentstehung bei Spiegeln 2.2.1 Ebener Spiegel Die Abbildungsgleichung des ebenen Spiegels ergibt sich aus der Konstruktion mit Hilfe des Reflexionsgesetzes. a a' keine Bildfehler P’ P seitenverkehrtes aber aufrechtes Bild virtuelles Bild P und P’ liegen auf der Normalen zur Spiegelfläche. Reelle und virtuelle Abbildungen Ein abbildendes optisches System lenkt die von einem Objektpunkt P ausgehenden Strahlen so ab, dass ein Beobachter hinter dem optischen System annimmt, das Licht kommt vom Bildpunkt P’. a) reelle Abbildung Im Bildpunkt vereinigen sich real existierende Lichtstrahlen (= Energie in P’ vorhanden). Ein Beobachter sieht die von diesem Punkt ausgehenden Lichtstrahlen. Ein reelles Bild kann mit einem Schirm aufgefangen werden. opt. System P b) virtuelle Abbildung Kein Schnittpunkt von realen Strahlen! Im Bildpunkt vereinigen sich die (rückwärtigen) Verlängerungen der Lichtstrahlen (= keine Energie in P’ vorhanden, nicht fotografierbar). Ein Beobachter hat den Eindruck, das Bild kommt von P’. Ein virtuelles Bild kann nicht mit einem Schirm aufgefangen werden. P P’ opt. System P’ Physik PHB3/4 (Schwingungen, Wellen, Optik) Seite 04_GeomOptikAbbildung1_BA.doc - 3/5 Beispiel: Durch die Wand schauen. Von welchen Stellen hinter der Wand sieht man das Bild ? 2.2.2 Sphärischer Spiegel (Kugelspiegel) Gaußscher Abbildungsbereich – Optik des Paraxialgebiets Alle Strahlen, die zur Abbildung beitragen, fallen unter einem geringen Neigungswinkel zur optischen Achse ein (= paraxiale Strahlen, achsennahe Strahlen). Wegen sin tan lautet das Brechungsgesetz in Paraxialnäherung: n n’ n n ' Aber: Darstellung des Strahlengangs meist durch nichtparaxiale Strahlen, wegen der besseren Übersicht. Konkavspiegel Achsenferne Strahlen am Konkavspiegel: Schnittpunkt mit der optischen Achse wandert für achsenferne und achsenparallele Strahlen in Richtung S kein punktförmiges Bild, sondern sog. Kaustik. Diesen Abbildungsfehler nennt man sphärische Aberration. Abhilfe: Ausblenden der achsenfernen Strahlen. Nichtsphärische Spiegeloberflächen für spezielle Abbildungen. ( Parabolspiegel, Rotationsellipsoid) Konvexspiegel Physik PHB3/4 (Schwingungen, Wellen, Optik) Seite 04_GeomOptikAbbildung1_BA.doc - 4/5 Abbildungsgleichung Die optische Achse wird durch den Objektpunkt O und den Kugelmittelpunkt M bestimmt. Der Scheitel S ist der Durchstoßpunkt der opt. Achse durch den Spiegel. Im paraxialen Fall fällt der Punkt A mit dem Lot auf den Scheitel zusammen. A h S O M O’ (-)a’ (-)r (-)a Berechnung mit Hilfe der Trigonometrie und dem Reflexionsgesetz. ' wegen ' tan h / a tan h / r oben eingesetzt ergibt: h h h h r a' a r tan h / a ' 1 1 2 a a' r Abbildungsgleichung für Kugelspiegel Die Abbildungsgleichung ordnet jedem Gegenstandspunkt O auf der optischen Achse einen Bildpunkt O’ zu. Definition Brennpunkt F und Brennweite f Der Brennpunkt F ist der Bildpunkt auf der optischen Achse, dessen Objektpunkt im Unendlichen liegt. Für a (-)) wird die Abbildungsgleichung zu 1/a’ = 2/r. Die Brennweite ist dann f = a’ = r/2. 1 1 1 a a' f mit f r 2 Aus der Definition des Brennpunktes und dem Reflexionsgesetz folgen die Regeln für die Bildkonstruktion: Parallelstrahl Brennstrahl Mittelpunktstrahl wird Brennstrahl wird Parallelstrahl wird Mittelpunktstrahl Physik PHB3/4 (Schwingungen, Wellen, Optik) Seite 04_GeomOptikAbbildung1_BA.doc - 5/5 y S M y’ F (-)a’ (-)a Abbildungsmaßstab3 ' y' a' y a 2.3 Bildentstehung bei Linsen Modellvorstellung zur Linsenwirkung: Strahlablenkung durch unterschiedliche Prismenstücke Im allgemeinen werden rotationssymmetrische (meist Kugelflächen) verwendet. Zerstreuungslinse Sammellinse Übersicht der wichtigsten Linsenarten. Zerstreuungslinsen Sammellinsen Bikonvex Plankonvex r1 > 0 r2 < 0 r1 r2 < 0 f'>0 f'>0 Positiver Meniskus r1 < 0 r2 < 0 Bikonkav Plankonkav Negativer Meniskus r1 < 0 r2 > 0 r1 < 0 r2 < 0 f'>0 f' <0 r1 r2 > 0 f' <0 f' <0 3 Der Abbildungsmaßstab ist ein Streckenverhältnis und darf nicht mit der Vergrößerung von opt. Instrumenten verwechselt werden.