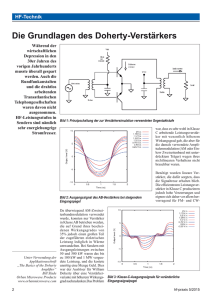
Aufbau und Charakterisierung eines

Wissenschaftliche Prüfungsarbeit im Fach
Physik
gemäß §12 der Landesverordung über die Erste Staatsprüfung für das Lehramt an
Gymnasien vom 07. Mai 1982, in der derzeit gültigen Fassung
Aufbau und Charakterisierung eines
rauscharmen kryogenen Verstärkers zur
Messung der Bewegungsfrequenz eines
einzelnen Ions in einer Penningfalle
Reinhard Heinke
vorgelegt am: 23. Oktober 2012
Institut für Physik der Johannes Gutenberg-Universität in Mainz
Erstgutachter:
Zweitgutachter:
Prof. Dr. J. Walz
PD Dr. F. Fiedler
Inhaltsverzeichnis
1 Einleitung
1
2 Die Penningfalle
5
2.1
Die ideale Penningfalle . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.2
Die reale Penningfalle . . . . . . . . . . . . . . . . . . . . . . . . . .
10
2.2.1
Fehler im elektrischen Feld
. . . . . . . . . . . . . . . . . . .
10
2.2.2
Fehler im magnetischen Feld . . . . . . . . . . . . . . . . . . .
12
2.3
Bestimmung des g-Faktors eines Teilchens in der Penningfalle . . . .
13
2.4
Die Mainzer Doppelfalle . . . . . . . . . . . . . . . . . . . . . . . . .
18
2.5
Die Phasenmethode
19
. . . . . . . . . . . . . . . . . . . . . . . . . . .
3 Die Detektionseinheit
3.1
23
Grundlegendes Prinzip . . . . . . . . . . . . . . . . . . . . . . . . . .
23
3.1.1
Der Parallelschwingkreis . . . . . . . . . . . . . . . . . . . . .
26
3.2
Das Teilchen als Reihenschwingkreis . . . . . . . . . . . . . . . . . .
28
3.3
Dip-Detektion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
30
3.4
Peak-Detektion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
34
3.5
Anforderungen an das Detektionssystem . . . . . . . . . . . . . . . .
36
4 Der kryogene Verstärker
4.1
39
Feldeffekt-Transistoren (FETs) . . . . . . . . . . . . . . . . . . . . .
39
4.1.1
FET-Grundschaltungen . . . . . . . . . . . . . . . . . . . . .
41
4.2
Rauschen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
43
4.3
Parasitäres Feedback . . . . . . . . . . . . . . . . . . . . . . . . . . .
48
4.4
Design . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
50
4.5
Experimentelle Ergebnisse . . . . . . . . . . . . . . . . . . . . . . . .
55
4.5.1
Der Pulsrohr-Kühler . . . . . . . . . . . . . . . . . . . . . . .
55
4.5.2
Verstärkung . . . . . . . . . . . . . . . . . . . . . . . . . . . .
56
4.5.3
Leistungsaufnahme . . . . . . . . . . . . . . . . . . . . . . . .
58
4.5.4
Spannungsrauschen . . . . . . . . . . . . . . . . . . . . . . . .
60
4.6
4.5.5
Der Resonator im Teststand . . . . . . . . . . . . . . . . . . .
64
4.5.6
Eingangskapazität . . . . . . . . . . . . . . . . . . . . . . . .
68
4.5.7
Eingangswiderstand . . . . . . . . . . . . . . . . . . . . . . .
71
4.5.8
Stromrauschen . . . . . . . . . . . . . . . . . . . . . . . . . .
73
Untersuchung des Eingangswiderstands . . . . . . . . . . . . . . . . .
75
4.6.1
DC-Eingangswiderstand . . . . . . . . . . . . . . . . . . . . .
75
4.6.2
Modell zur kapazitiven Kopplung zwischen Gate und Drain der
EingangsFETs . . . . . . . . . . . . . . . . . . . . . . . . . .
4.7
Zusammenfassung und Signal-Rausch-Verhältnis
5 Zusammenfassung und Ausblick
. . . . . . . . . . .
79
86
95
Abbildungsverzeichnis
2.1
Penningfalle (schematisch) . . . . . . . . . . . . . . . . . . . . . . . .
6
2.2
Quadrupolpotential . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
2.3
Bewegungsmoden in der Penningfalle . . . . . . . . . . . . . . . . . .
8
2.4
Zylindrische 5-Pol-Falle mit Korrekturelektroden . . . . . . . . . . .
12
2.5
Magnetische Flasche (schematisch) . . . . . . . . . . . . . . . . . . .
15
2.6
Magnetisches Feld in der Analysefalle . . . . . . . . . . . . . . . . . .
16
2.7
Änderung des Potentials eines Teilchens mit Spin . . . . . . . . . . .
17
2.8
Doppelfalle (schematisch) . . . . . . . . . . . . . . . . . . . . . . . .
19
2.9
Veranschaulichung der Phasenmethode . . . . . . . . . . . . . . . . .
20
2.10 Messablauf der Phasenmethode . . . . . . . . . . . . . . . . . . . . .
21
3.1
Falle mit Parallelschwingkreis . . . . . . . . . . . . . . . . . . . . . .
25
3.2
Resonanzkurve (schematisch) . . . . . . . . . . . . . . . . . . . . . .
28
3.3
Detektionsprinzip . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
29
3.4
Dip mit wichtigen Kennzahlen . . . . . . . . . . . . . . . . . . . . . .
32
3.5
Detektionseinheit mit Verstärker . . . . . . . . . . . . . . . . . . . .
33
3.6
Peak (schematisch) . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
4.1
Schematische Darstellung der Funktionsweise eines MESFETs . . . .
40
4.2
Transistor-Grundschaltungen . . . . . . . . . . . . . . . . . . . . . .
41
4.3
Kaskodenschaltung . . . . . . . . . . . . . . . . . . . . . . . . . . . .
42
4.4
Ersatzschaltung eines rauschenden Widerstandes . . . . . . . . . . .
44
4.5
Schematische Darstellung zu internen Rauschquellen des Verstärkers
47
4.6
Skizze zum parasitären Feedback eines FETs . . . . . . . . . . . . . .
48
4.7
Schaltschema des Verstärkers . . . . . . . . . . . . . . . . . . . . . .
50
4.8
Beschriftete Fotografie des Verstärkers . . . . . . . . . . . . . . . . .
52
4.9
Parallelschaltung von Rauschquellen . . . . . . . . . . . . . . . . . .
53
4.10 Pulsrohrkühler . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
55
4.11 Verstärkung bei verschiedenen Arbeitspunkten
57
. . . . . . . . . . . .
4.12 Leistungsaufnahme bei verschiedenen Arbeitspunkten . . . . . . . . .
59
4.13 Schematischer Messaufbau zur Rauschmessung . . . . . . . . . . . .
61
4.14 Spannungsrauschen bei verschiedenen Arbeitspunkten . . . . . . . .
63
4.15 Spannungsrauschen in Abhängigkeit der Frequenz . . . . . . . . . . .
64
4.16 Gehäuse des Resonators . . . . . . . . . . . . . . . . . . . . . . . . .
65
4.17 Schematische Darstellung der Ankopplung des Testresonators . . . .
66
4.18 Transferfunktion des Resonators . . . . . . . . . . . . . . . . . . . . .
67
4.19 Schematische Darstellung zur Messung von Eingangskapazität und Widerstand des Verstärkers . . . . . . . . . . . . . . . . . . . . . . .
69
4.20 Eingangskapazität bei verschiedenen Arbeitspunkten . . . . . . . . .
70
4.21 Eingangswiderstand bei verschiedenen Arbeitspunkten . . . . . . . .
72
4.22 Kennlinien des Gate-Source-Widerstands der Eingangs-FETs
. . . .
76
4.23 DC-Widerstand der Gate-Source-Strecke der Eingangs-FETs . . . . .
77
4.24 Kurvenanpassung an den Gate-Source-Widerstand der Eingangs-FETs
zur Ermittlung des differentiellen Eingangswiderstands . . . . . . . .
78
4.25 Modell zur Untersuchung des Eingangswiderstands auf Grund der
Gate-Drain-Kapazität . . . . . . . . . . . . . . . . . . . . . . . . . .
79
4.26 Impedanztransformation beim Modell zum Eingangswiderstand . . .
80
4.27 Drain-Source-Widerstand der Eingangs-FETs in Abhängigkeit der Spannung an Gate 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
82
4.28 Modellanpassung an Messwerte . . . . . . . . . . . . . . . . . . . . .
83
4.29 Vergleich des Eingangswiderstandes für einen und zwei Eingangs-FETs 85
4.30 Vergleich der Eingangskapazität für einen und zwei Eingangs-FETs .
86
4.31 SNR in Abhängigkeit des Kopplungsfaktor . . . . . . . . . . . . . . .
88
4.32 Rauschspektrum des Teststandresonators . . . . . . . . . . . . . . . .
89
4.33 Effektiver Parallelwiderstand des Nachweiskreises gegen Ankopplung
des Verstärkers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
90
4.34 Breite des Dips gegen Abkopplung des Verstärkers für verschiedene
effektive Elektrodenabstände . . . . . . . . . . . . . . . . . . . . . .
91
4.35 Breite des Dips gegen effektiven Elektrodenabstand . . . . . . . . . .
92
4.36 Signal-Rausch-Verhältnis bei Peak-Detektion gegen Ankopplung des
Verstärkers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
93
Tabellenverzeichnis
2.1
Bewegungsfrequenzen im Protonexperiment . . . . . . . . . . . . . .
9
3.1
Effektive Elektrodenabstände . . . . . . . . . . . . . . . . . . . . . .
24
1 Einleitung
Die präzise experimentelle Bestimmung fundamentaler physikalischer Konstanten ist
eine wichtige Aufgabe der modernen Physik. Sie ist wichtig, um abgeleitete Größen
oder anhand einer Theorie erwartete Beobachtungen in einem Experiment möglichst
präzise vorherzusagen. Eine Abweichung zwischen Experiment und Theorie liefert
dabei stets Hinweise auf Mängel der Theorie oder bisher unentdeckte physikalische
Phänomene jenseits der bekannten Modelle.
Das derzeitige Standardmodell der Elementarteilchenphysik unterliegt wie jede lokal relativistische Theorie dem CP T -Theorem. Es besagt, dass jeder physikalische
Vorgang durch gleichzeitige Transformation der Zeit T (eine Umkehrung des zeitlichen Ablaufs), der Parität P (eine Inversion aller Raumkoordinaten der beteiligten
Teilchen und Strukturen) sowie der Ladung C (und damit einem Austausch der Teilchen mit ihren Antiteilchen) in einen Vorgang überführt werden kann, der ebenfalls
mit den Gesetzen der Physik in Einklang liegt. Aus ihm folgt, dass alle existierenden Teilchen die gleichen Eigenschaften haben wie ihre Antiteilchen, wie die gleiche
Masse, die entgegengesetzte (aber betraglich gleiche) Ladung oder die identische Lebensdauer. Außerdem müssen ihre magnetischen Momente exakt übereinstimmen
[Lüd57]. Über einen Vergleich dieser Größe bei Proton und Antiproton ist also ein
Test des Standardmodells möglich.
In viele Experimenten ist eine Verletzung der Symmetrie bei alleiniger Inversion
der Größen C, P und T sowie dem Produkt CP festgestellt worden. Ein Nachweis
der CP T -Verletzung wurde bislang nicht beobachtet. Besonders eindrucksvoll ist der
Vergleich der Massen des K-Mesons und seines Antiteilchens [Sch95]:
|mK 0 − mK̄ 0 |
< 1, 3 · 10−18
mK 0
(1.1)
Hierbei handelt es sich allerdings nicht um ein direkt gemessenes Ergebnis, da weitere Modellrechnungen eingingen.
1
1 Einleitung
In weiteren Experimenten haben sich Penningfallen zum Speichern der Teilchen bei
Messung des CP T -Theorems bewährt. Im leptonischen Sektor ist dabei der Vergleich
der magnetischen Momente g von Elektron und Positron hervorzuheben [Deh87]
|ge− − ge+ |
= (−0, 5 ± 2, 1) · 10−12
ḡ
(1.2)
Ziel des Mainzer Proton-Experimentes ist die präzise Bestimmung und der Vergleich der g-Faktoren von Proton und Antiproton. Der bisher genaueste gemessene
Wert für das Proton stammt aus dem Jahre 1975 [Kle75]. In diesem Experiment
wurde der Hyperfeinübergang eines Wasserstoff-Masers in einem Magnetfeld spektroskopisch untersucht. Es wurde eine Präzision von 10−8 erreicht und ein Wert von
g
= 2, 792847353(28)
2
(1.3)
bestimmt. Zu beachten ist jedoch, dass es sich hierbei um ein gebundenes Proton
handelt.
Für das magnetische Moment des Antiproton existiert eine Bestimmung über die
Hyperfeinstruktur von antiprotonischem Helium. Sie stammt aus dem Jahr 2009.
Hier ergab sich eine Präzision von 3 · 10−3 [Pas09].
Mit dem Mainzer Proton-Experiment wird somit erstmals eine g-Faktor-Messung
am „nackten“, ungebundenen Proton durchgeführt. Die Realisierung folgt einem Vorschlag von W. Quint aus dem Jahr 1993 [Qui93]. Dabei wird eine Präzision von 10−9
angestrebt, was eine Verbesserung der Genauigkeit des Wertes für das Antiproton
von 6 Größenordungen bedeutet. Nachdem das Experiment in Mainz mit Protonen
durchgeführt wurde, kann es an eine Antiprotonenquelle, etwa den AD am CERN
oder dem FLAIR an der GSI umziehen und dort betrieben werden.
Die Messung des g-Faktors erfolgt über die in den Fallenwänden induzierten Spiegelströme. Sie bilden direkt die Eigenfrequenzen des in der Falle gespeicherten Teilchens ab. Eine hohe experimentelle Herausforderung ist es, diese Signale eines einzelnen, einfach geladenen Teilchens sichtbar zu machen. Die vorliegende Arbeit behandelt den Aufbau und die Charakterisierung eines rauscharmen, in kryogener Umgebung arbeitenden Verstärkers zu diesem Zweck. Sie ist wie folgt gegliedert:
In Kapitel 2 wird die Penningfalle für das Einzel-Teilchen-Experiment vorgestellt.
2
Die Bewegungsmoden des Teilchens werden diskutiert und die Grundlagen zur zerstörungsfreien Messung erläutert. Die Besonderheiten der Mainzer Doppelfalle aus
Analyse- und Präzisionsmodul werden dargestellt.
Kapitel 3 gibt eine Erklärung der verwendeten Detektionsmethoden. Es wird abgeleitet, welche Anforderungen an die elektronische Detektionseinheit und insbesondere
den ersten Verstärker gestellt sind.
In Kapitel 4 wird der neu konstruierte Verstärker beschrieben. Die Ergebnisse zu
den Messungen in kryogener Umgebung werden dargestellt und in Bezug auf das
Proton-Experiment bewertet.
Abschließend gibt Kapitel 5 eine kurze Zusammenfassung und einen Überblick über
den aktuellen Stand und die Zukunft des Experiments.
3
2 Die Penningfalle
Als Vorrichtung zur Speicherung geladener Teilchen sind im Laufe der Zeit verschiedene Techniken entwickelt worden, die mit statischen oder dynamischen elektrischen
und magnetischen Feldern operieren. Eine Technik, die Penningfalle ermöglicht die
Speicherung von Ionen durch die Überlagerung eines homogenen statischen Magnetfeldes mit einem statischen elektrischen Quadrupolfeld. Nach dem Theorem von
Earnshaw ist die Erzeugung eines stabilen Gleichgewichtspunkts für ein Ion nicht
allein durch statische magnetische oder statische elektrische Felder möglich, so dass
eine solche Kombination nötig ist. Die Bewegung des Teilchens in der Falle kann als
Überlagerung dreier harmonischer Oszillatoren beschrieben werden. Aus der Messung der Frequenzen dieser Oszillationen lässt sich das magnetische Moment des
Ions bestimmen.
Zunächst wird die Funktionsweise der idealen Penningfalle beschrieben, danach
die Modifikationen bei Betrachtung einer realen Falle sowie die Grundlagen der Bestimmung des magnetischen Moments eines Teilchens in der Falle.
2.1 Die ideale Penningfalle
~ = B0 ebz zwingt ein geladenes Teilchen auf
Ein homogenes, statisches Magnetfeld B
Grund der Lorentzkraft auf eine Zyklotronbahn senkrecht zu den Magnetfeldlinien.
Somit ist das Teilchen radial in der x-y-Ebene gefangen. Die Speicherung entlang der
axialen z-Achse gelingt duch die Superpostition eines statischen elektrischen Feldes,
das ein Potentialminimum aufweist. Abbildung 2.1 zeigt schematisch den Aufbau.
Zur Realisierung verwendet man ein Quadrupolpotential der Form
V0 z 2 −
Φ=
2
d2
ρ2
2
(2.1)
Dabei ist V0 die Spannung zwischen der Ringelektrode und den beiden Endkappen,
z die axiale und ρ die radiale Raumkoordinate.
5
2 Die Penningfalle
Abbildung 2.1: Schematische Darstellung einer Penningfalle mit hyperbolischen
Elektroden. Zwischen der Ringelektrode und beiden Endkappen wird
die Fallenspannung V0 angelegt, um das Teilchen in axialer Richtung
zu speichern. Überlagert ist ein homogenes Magnetfeld B zur Speicherung in axialer Richtung. z0 und ρ0 bezeichnen die Abstände zu
den Fallenelektroden.
1
d=
2
z02
ρ2
− 0
2
(2.2)
ist ein typischer Fallenparameter, wobei z0 und ρ0 den Abstand zwischen Fallenzentrum und den felderzeugenden Endkappen bzw. Ringelektroden beschreiben.
Das Potential ist in Abbildung 2.2 dargestellt. Zur Erzeugung werden hyperbolisch
geformte Elektroden verwendet, die wie die Äquipotentiallinien der Gleichung
ρ2 z 2
−
= ±1
ρ20 z02
(2.3)
genügen. Um das Feld in Idealform zu erzeugen, müssten diese Elektroden sich ins
Unendliche erstrecken.
Die Bewegungsgleichungen für geladene Teilchen sind durch die Lorentzkraft bestimmt:
~ +ρ
~ =0
mρ
~¨ − q E
~˙ × B
für die radiale Richtung und
6
(2.4)
2.1 Die ideale Penningfalle
Abbildung 2.2: Schematische Darstellung des elektrischen Quadrupolpotentials in
der Falle. z ist die axiale, ρ die radiale Richtung. Darunter ist der
Verlauf der Äquipotentiallinien dargestellt
mz̈ +
qV0 z
=0
d2
(2.5)
für die axiale Richtung. Dabei bezeichnet m die Masse und q die Ladung des Teilchens. Die Differentialgleichungen beschreiben die Bewegung dreier harmonischer
Oszillatoren und sind analytisch lösbar. Es ergeben sich drei entkoppelte Bewegungsmoden, die durch ihre Eigenfrequenzen charakterisiert sind.
In axialer Richtung erhält man eine Bewegungsmode, die nicht vom magnetischen
Feld abhängt und alleine durch die Potentialdifferenz zwischen den Elektroden sowie
den Fallenparameter d gegeben ist:
r
ωz =
qV0
md2
(2.6)
Die Mode beschreibt die Schwingung des Teilchens in axialer Richtung um das
Fallenzentrum auf Grund des elektrischen Feldes. Hieraus ist die Motivation für die
Verwendung eines Quadrupolpotentials ersichtlich, da sich so eine harmonische Oszillation ohne Abhängigkeit der Energie von der Amplitude ergibt.
Die Lösung der Differentialgleichung in radialer Richtung ergibt zwei Eigenfrequenzen,
7
2 Die Penningfalle
ωc
ω+ =
+
2
r
ω 2
ωc
ω− =
−
2
r
ω 2
c
2
−
ωz2
2
(2.7)
−
ωz2
2
(2.8)
sowie
c
2
mit der freien Zyklotronfrequenz
ωc =
q
B0
m
(2.9)
Die Mode der Frequenz ω+ wird als reduzierte Zyklotronfrequenz bezeichnet. Im
Wesentlichen handelt es sich dabei um die Zyklotronbewegung um die Magnetfeldlinien, modifiziert durch den Anteil des elektrischen Quadrupolfeldes, der das Teilchen
entgegen der Lorentzkraft nach außen, zur Ringelektrode hin, zieht.
Die zweite Frequenz ω− entspricht der Magnetronbewegung. Die radial weisende
Komponente des elektrischen Feldes bewirkt eine Bewegung des Teilchens zur Ringelektrode hin, woraus in Kombination mit der Lorentzkraft eine Kreisbewegung um
die Magnetfeldlinien resultiert.
Abbildung 2.3: Bewegung eines Ions in der Penningfalle: Magnetron- und modifizierte Zyklotronbewegung in der x-y-Ebene, harmonische Schwingung in Richtung der axialen z-Achse. Die resultierende Gesamtbewegung ist ist eine Überlagerung der drei Bewegungsmoden (in schwarz
dargestellt).
8
2.1 Die ideale Penningfalle
Mode
ωz
ω−
ω+
Tabelle 2.1: Größenordung
der
Protonexperiment
Frequenz
2π· 690 kHz
2π· 7 kHz
2π· 29 MHz
Bewegungsfrequenzen
des
Teilchens
im
Die Gesamtbewegung ist eine Überlagerung aller drei Bewegungsmoden, wie in
Abbildung 2.3 dargestellt. Die im Proton-Experiment vorliegenden Frequenzen sind
in Tabelle 2.1 aufgeführt.
Zwischen den Moden lässt sich eine nützliche Beziehung ableiten:
2
2
ωc2 = ω+
+ ω−
+ ωz2
(2.10)
Diese Relation, das so genannte Invarianztheorem [Bro82], wird für die weitere
Behandlung äußerst wichtig sein, da es auch für eine nicht-ideale Realisierung der
Penningfalle Gültigkeit besitzt.
Da die Bewegungsmoden voneinander entkoppelt sind, lässt sich die Gesamtenergie des gefangenen Teilchens aus der Summe der Einzelenergien berechnen. In der
quantenmechanischen Betrachtung ergibt sich dabei je eine Quantisierung gemäß des
harmonischen Oszillators. Unter Berücksichtigung der Präzession des Spins um die
Magnetfeldachse ergibt sich somit die Gesamtenergie
1
1
1
E = ~ωz (nz + ) + ~ω+ (n+ + ) − ~ω− (n− − ) + ~ωL mL
2
2
2
(2.11)
mit den Quantenzahlen der Bewegungsmoden nz , n+ und n− sowie der Larmorfrequenz ωL , die die Präzession des Spins darstellt, mit dazugehöriger magnetischer
Quantenzahl mL .
Zu beachten ist dabei die Auswirkung der Quantenzahl n− der Magnetronmode.
Eine Erhöhung bewirkt eine Verringerung der Energie und ein Aufweiten des Bahnradius. Die Mode ist metastabil. Dies ist anschaulich ersichtlich, da sich das Teilchen
auf dieser Mode um das Maximum des elektrischen Potentials bewegt, das radial
abnimmt. Es wird also nach außen gezogen. Wird der Radius der Magnetronbahn zu
groß, kann das Teilchen an den Fallenelektroden verloren gehen. Dies ist im Betrieb
wichtig, da etwa durch Wechselwirkung mit Restgasatomen Energie dissipiert werden
kann [Ame05].
Die Energie der Bewegungen kann durch Anregung mit externen elektrischen
9
2 Die Penningfalle
Wechselfeldern geändert werden. Zum einen kann eine Erhöhung der Energie nötig sein, um die Bewegungsamplitude zur besseren Detektion zu vergrößern. Zum
anderen, um unerwünschte Teilchen aus der Falle zu entfernen, indem diese an die
Fallenelektroden stoßen oder aus dem Raumbereich der harmonischen Oszillation
gebracht werden.
2.2 Die reale Penningfalle
Im realen Aufbau kommt es unweigerlich zu Abweichungen von den oben beschriebenen idealen Voraussetzungen. So können die Elektroden nicht unendlich groß aufgebaut werden, was für ein perfektes elektisches Quadrupolfeld nötig wäre. In diesem
Experiment, wie in vielen anderen, die Penningfallen verwenden, wird unter anderem
deswegen auf eine zylindrische Falle zurückgegriffen [Gab89]. Diese hat weiterhin den
Vorteil, dass sie analytisch beschreibbar bleibt [Kre08]. Des Weiteren wird eignet sich
diese Anordnung, wie weiter unten genauer beschrieben, zum einfachen Einbringen
neuer Teilchen sowie zum Anordnen mehrerer Fallen in einer Reihe.
Das Quadrupolpotential wird durch weitere Effekte gestört. So kann es an den
Fallenelektroden zu Kontaktpotentialen kommen, die Auswirkungen auf das Feld
haben. Ebenso wird dieses durch eventuell vorhandene mehrere Teilchen in der Falle beeinflusst. Fertigungsfehler der Elektroden können nicht ausgeschlossen werden,
ebenso eine Abweichung von der idealen Rotationssymmetrie. Auch das magnetische
Feld kann Inhomogenitäten aufweisen oder eine Verkippung gegenüber der Falle aufweisen, so dass die Symmetrieachse des elektrischen Feldes und die Richtung der
Magentfeldlinien nicht mehr übereinstimmen.
Diese Abweichungen äußern sich in einer möglichen Abhängigkeit der Eigenfrequenzen der gespeicherten Teilchen von ihrer Energie, i.e. Amplitude. Auch können
Kopplungen zwischen den oben beschriebenen Bewegungsmoden auftreten. Das bedeutet, dass die Frequenz einer Mode von der Energie mindestens einer anderen Mode
abhängig ist.
2.2.1 Fehler im elektrischen Feld
Die zylindrische Falle kann analytisch durch eine Multipolentwicklung des elektrischen Feldes beschrieben werden, welche die Abweichungen vom idealen Quadrupolpotential quantifiziert. Die Entwicklung des Potentials für axiale Symmetrie lautet
in Zylinderkoordinaten mit dem Abstand ρ vom Zentrum und Polarwinkel cos θ =
10
z
ρ
2.2 Die reale Penningfalle
Φ(ρ, θ) =
∞
V0 X ρ i
Pi (cos θ)
Ci
2
d
(2.12)
i=0
Dabei sind Pi die Legendre-Polynome der Ordnung i. Die Koeffizienten Ci geben
somit die Stärke der jeweiligen Korrektur an. Üblicherweise ist die Amplitude der
Bewegung in ρ-Richtung klein gegenüber dem Fallenparameter d, somit ist
ρ
d
immer
kleiner als 1. Somit fallen höhere Ordnungen weniger stark ins Gewicht.
Die Ordnungen beeinflussen die Bewegung des Teilchens auf verschiedene Weise
• C0 : Dies ist ein konstanter, ortsunabhängiger Beitrag zum Feld, der in den
Bewegungsgleichungen keine Rolle spielt.
• C1 : Dieser Beitrag liefert eine konstante elektrische Kraft, die das Zentrum die
Oszillation entlang der z-Achse verschiebt. Die Frequenz der Schwingung wird
dadurch nicht beeinflusst.
• C2 : Hierdurch wird der Quadrupolanteil beschrieben, der die rücktreibende
elektrische Kraft für die Oszillation liefert. Er beeinflusst die Frequenz der
axialen Schwingung aus Gleichung 2.6 gemäß
r
ωz =
C2
qV0
md2
(2.13)
• C3 , C5 , ...: Höhere ungerade Ordnungen der Multipolentwicklung bewirken eine
Energieabhängigkeit der Eigenfrequenzen. Aufgrund der Symmetrie der Falle
sind sie aber zu vernachlässigen.
• C4 , C6 , ...: Die geraden höheren Multipolordnungen überwiegen die ungeraden
auf Grund der Symmetrie der Anordnung. Auch sie führen auf eine Amplitudenabhängigkeit der Eigenfrequenzen sowie zu einer Kopplung der Moden.
Zur Kompensierung der Inharmonizitäten werden im Experiment Korrekturelektroden in die Falle eingebracht. Abbildung 2.4 zeigt dies für die zylindrische Ausführung. Dadurch gewinnt man mit dem Spannungsverhältnis zwischen Ring- und
Korrekturelektrode einen weiteren Freiheitsgrad, um das Feld zu beeinflussen. Eine
Kompensation der höheren Korrekturterme ist durch eine geeignete Wahl der Spannungen an den Korrekturelektroden möglich.
11
2 Die Penningfalle
Abbildung 2.4: Zylindersymmetrische 5-Pol-Falle mit Korrekturelektroden. Rechts
ist der resultierende Potentialverlauf auf den Oberflächen zu sehen.
Dabei ist U0 die Spannung an der eigentlichen Ringelektrode, die
Korrekturelektroden liegen auf Uk , die Endkappen auf Masse.
2.2.2 Fehler im magnetischen Feld
Das Magnetfeld wird durch einen supraleitenden Magneten erzeugt. Dieser kann Inhomogenitäten aufweisen. Die Fallenkomponenten bewirken auf Grund ihrer endlichen Suszeptibilität ebenfalls eine Verzerrung der Magnetfeldlinien. Das Magnetfeld
in z-Richtung lässt sich durch eine quadratische Funktion approximieren:
1 2
2
Bz = B0 − B1 z + B2 z − ρ
2
(2.14)
Wie bei der Diskussion des elektrischen Feldes ist B1 auf Grund der Symmetrie
klein, weswegen die Kopplung der Bewegungsmoden hauptsächlich auf den Einfluss
der geraden Korrekturordnungen, repräsentiert durch B2 , zurückzuführen ist [Bro86].
Zur präzisen Messung der Eigenfrequenzen ist also eine Minimierungen der geraden
Korrekturordnungen nötig. Allerdings ist für die Detektion des Spinzustandes eines
Teilchens eine hohes B2 nötig, wie weiter unten beschrieben.
Weitere Limitierungen in der Güte der Messung, die durch den Magneten beeinflusst werden, sind das zeitliche Driften sowie Fluktuationen im Magnetfeld. Deutlich
wird dies beispielsweise bei Experimenten zum Massenvergleich von Teilchen, wo auf
Grund des Zeitverzugs beim Einbringen neuer Teilchen Fluktuationen von
δB
B
≈ 10−9
die Genauigkeit limitieren können [Gab99]. Ein weiterer Einfluss ist durch den Ef-
12
2.3 Bestimmung des g-Faktors eines Teilchens in der Penningfalle
fekt des Flusskriechens gegeben. Dabei wandern magnetische Flussschläuche durch
die ortsfesten Vortizes und nehmen einen Zustand geringerer Energie an. Die induzierten Ströme können den supraleitenden Magneten lokal aufwärmen und damit
Feldänderungen verursachen. Dieser Prozess läuft allerdings auf einer großen Zeitskala ab und kann auf Grund seiner Linearität gut extrapoliert werden [Kel03]. Zur
Reduzierung dieser einschränkenden Effekte bieten sich grundsätzlich zwei Ansätze
an. Zum einen kann das magnetische Feld selbst aktiv oder passiv stabilisiert werden.
Dabei kann etwa eine weitere Spule verwendet werden, welche nach der Lenz’schen
Regel bei Magnetfeldänderungen ein Feld bewirkt, dass dieser Änderung entgegenwirkt. Dabei können nach [Jhe92] Unterdrückungen um einen Faktor 150 erreicht
werden. Weiterhin ist es möglich, die Magnetfeldänderungen zu messen und aktiv
über zusätzliche Spulen eine Kompensation durchzuführen. Zum anderen ist eine
Temperaturstabilisierung des Magneten über den Druck des kühlenden Helium möglich. Nach [VD99] ist damit eine Stabilität von 17(2) · 10−12 pro Stunde zu erreichen.
Eine weitere Quelle für unerwünschte Kopplungen der Bewegungsmoden ist die
Verkippung der Falle gegenüber dem Magnetfeld. Jedoch behält das Invarianztheorem 2.10 dabei seine einfache Form bei [Bro86], es gilt
ωc2 = ω 2+ + ω 2− + ω 2z
(2.15)
mit den durch die Verkippung modifizierten Frequenzen ω + , ω − und ω z . Dies
ist besonders nützlich, da weiterhin die aus direkten Messungen nicht zugängliche
freie Zyklotronfrequenz bestimmt werden kann. Beim Realen Aufbau der Falle sind
solche Verkippungen nicht zu vermeiden, womit man mit dem Invarianztheorem ein
mächtiges Werkzeug an der Hand hat.
2.3 Bestimmung des g -Faktors eines Teilchens in der
Penningfalle
Die präzise Bestimmung des g-Faktors des Protons ist das Ziel des Experiments. Hier
wird dargestellt, wie man durch die Detektion der oben genannten Eigenfrequenzen
den Wert des g-Faktors bestimmen kann.
Der g-Faktor eines Protons gibt die Proportionalität zwischen dem magnetischen
~ wieder. Eine ÄndeMoment µ
~ und dem Kernmagneton µK bezogen auf den Spin S
rung der Spinquantenzahl um zwischen den quantenmechanisch erlaubten Zuständen
13
2 Die Penningfalle
+ 12 und − 12 bedeutet damit eine Erhöhung des magnetischen Moments um gµK .
~
S
µ
~
=g
µK
~
(2.16)
Sichtbar wird der Einfluss des Spins in der Energieverschiebung in einem Magnetfeld. Der Spin des Teilchens ist dabei entweder parallel oder antiparallel zum Feld
ausgerichtet. Es gilt
∆E = gµ
~
∆S
~ = g e~ B
B
~
2m
(2.17)
bei einer Änderung des Spinzustands um 1, was einer Änderung des Spins um ~
entspricht. Um experimentell Zugang zu erhalten, müssen zwei Frequenzen bestimmt
werden. Zum einen ist dies die oben erwähnte Zyklotronfrequenz
ωc =
q
B
m
(2.18)
sowie die Präzessionsfrequenz des Spins in einem äußeren Magnetfeld der Larmorfrequenz
ωL = g
q
µK
B=g
B
~
2m
(2.19)
Aus dem Verhältnis ergibt sich der g-Faktor zu
g=2
ωL
ωc
(2.20)
Die Zyklotronfrequenz wird über das Invarianztheoriem 2.15 aus den messbaren
Bewegungsmoden bestimmt. Dabei sei darauf hingewiesen, dass nach der Fehlerbetrachtung
δωc =
ω+
ω−
ωz
δω+ +
δω− +
δωz
ωc
ωc
ωc
(2.21)
die reduzierte Zyklotronfrequenz am genauesten gemessen werden muss, da sie den
größten Beitrag liefert (vergleich Tabelle 2.1).
Die Larmorfrequenz ωL kann dagegen nicht direkt gemessen werden, da sie keiner Bewegung des Ions in der Falle entspricht (wie in Abschnitt 3 beschrieben wird,
werden die benötigten Frequenzen aus den in den Fallenwänden induzierten Spiegelströmen ermittelt). Abhilfe schafft man sich hier durch gezieltes Einfügen einer
Inhomogenität in das magnetische Feld. Die dafür verwendete spezielle Form die-
14
2.3 Bestimmung des g-Faktors eines Teilchens in der Penningfalle
ser Inhomogenität ist durch die magentische Flasche gegeben. Das Prinzip ist in
Abbildung 2.5 dargestellt.
Abbildung 2.5: Schematische Darstellung des Aufbaus einer magnetischen Flasche.
Der ferromagnetische Ring bewirkt eine Verzerrung der in axialer Richtung verlaufenden B-Feldlinien und damit eine Ortsabhängigkeit seiner Stärke. Im Experiment fungiert der Ring auch als
Fallenelektrode
Dabei wird durch die gezielte Einbringung eines ferromagnetischen Materials ein
Magnetfeld erzeugt, das in erster Näherung durch einen quadratisch mit dem Abstand zum Zentrum zunehmenden Term beschrieben werden kann:
~ = B2
∆B
ρ2
2
z −
~ez − zρ~eρ
2
(2.22)
Der Verlauf ist in 2.6 dargestellt.
Der radiale Anteil kann, wie in der Diskussion der elektrischen Multipolentwicklung, vernachlässigt werden. Die potentielle Energie des Teilchens ist dann gegeben
durch
Epot = qΦelektrisch − gµK mS (B0 + B2 z 2 ) = qΦelektrisch ± gµK (B0 + B2 z 2 ) (2.23)
mit Spinquantenzahl mS . Schematisch ist dies in 2.7 dargestellt.
Je nach Ausrichtung des Spins wird daher ein höheres oder flacheres Potential von
dem Ion überstrichen. Somit koppelt die Spinausrichtung an diese Bewegungsmode.
Die axiale Frequenz ergibt sich zu
15
2 Die Penningfalle
Abbildung 2.6: Magnetischer Feldverlauf in der Analysefalle, die als magnetische Flasche konzipiert ist. Es wurden die Parameter B0 = 0,85 T und B2 =
300 mT/mm2 gewählt.
r
ωz =
1 d2
Epot (z = 0) =
m dz 2
r
qV0 C2 2gµK B2
±
md2
m
(2.24)
Die Änderung der axialen Frequenz nach einem „Umklappen“ des Spins resultiert
in
δωz =
2gµK B2
mωz
(2.25)
Diese hier angewandte Methode verwendet den kontinuierlichen Stern-GerlachEffekt. Auf dieser Methode basierende Untersuchungen wurden in [Deh88] vorgeschlagen. Behandlungen für das Antiproton finden sich bei Quint et al. [Qui04],
Anwendungen werden von Häffner et al. [HW03] und Gabrielse [Han08] beschrieben.
Die Größenordnung kann man sich exemplarisch an den im Experiment realisierten
Parametern anschaulich machen. Die Fluktuationen der axialen Frequenz auf Grund
der Spannungsfluktuationen im elektrischen Potential ergeben sich über
1
δωz =
2
r
q
∆V
md2 V0
(2.26)
bei einem realisierten ∆V0 von etwa 600 nV zu
δωz ≈ 2π50mHz
16
(2.27)
2.3 Bestimmung des g-Faktors eines Teilchens in der Penningfalle
Potential
Spin down
ohne Spin
Spin up
Spin down
Spin up
z-Achse
Abbildung 2.7: Schematische Darstellung der Abhängigkeit des potentiellen Energie
eines spinbehafteten Teilchens in einem inhomogenen Magnetfeld in
Abhängigkeit seiner Spinorientierung. Die Aufspaltung ist stark überzeichnet. Die gegebenen Werte sind exemplarisch für das tatsächliche
Experiment.
Um eine um den Faktor 3 stärkere Verschiebung durch den Spinflip zu erhalten,
muss bei einer axialen Frequenz von etwa 700 kHz ein B2 von mindestens ca. 300
mT
mm2
erreicht werden. Daraus ergibt sich ein δωz von ca 2π175 mHz.
Um nun die den g-Faktor zu bestimmen, wird folgendes Messprinzip angewandt:
Zunächst werden die Zyklotronfrequenz ωc bestimmt. Gleichzeitig wird in die Falle
mit der Larmorfrequenz eingestrahlt, um einen Spinflip zu induzieren. Über g = 2 ωωCL
wird der g-Faktor berechnet, der sich aus den beiden Frequenzen ergibt. Anschließend
wird die Spin-Einstellung detektiert, bzw. nachgewiesen, ob ein Umklappen des Spins
stattgefunden hat. Das Vorgehen wird bei kontinuierlicher Veränderung der Larmorfrequenz wiederholt, da diese nicht genau bekannt ist. Das Maximum der erhaltenen
Wahrscheinlichkeitsverteilung für den Spinflip in Abhängigkeit der Einstrahlfrequenz
ergibt den gesuchten Wert des g-Faktors, da hier die gesuchte Larmorfrequenz liegt.
17
2 Die Penningfalle
2.4 Die Mainzer Doppelfalle
Bei der oben beschriebenen Vorgehensweise besteht eine grundlegende Schwierigkeit.
So wird für die Detektion der Spineinstellung eine möglichst große Inhomogenität B2
benötigt. Jedoch koppeln auch die Bewegungsmoden der Eigenfrequenzen des Teilchens über ihr magnetisches Moment an die magnetische Flasche. Die Bewegungsgleichungen sind nicht mehr analytisch lösbar, jedoch lässt sich unter Verwendung
der Störungstheorie eine Korrekturmatrix ableiten, wie in [Bro86] gezeigt. Dadurch
lässt sich die Frequenzänderung in Abhängigkeit von der Energie der reduzierten
Zyklotronbewegung angeben:
∆νz =
B2
1
E+
2
B0 4π mνz
(2.28)
Daraus wird kann der Einfluss auf die Genauigkeit der Messung des g-Faktors
errechnet werden [HW03]:
∆g = −g
νz
1
B2
2 ∆ν = −g B 4π 2 mν 2 E+
ν+
0
+
(2.29)
Schätzt man dies für eine Zyklotronmodentemperatur von 4K und einem B2 von
mT
300 mm
2 ab, erhält man eine Abweichung der Größenordnung
∆g
g
≈ 2 · 10−7 , was mit
der geforderten Präzision von 10−9 nicht vereinbar ist. In [HW03] wird die Verwendung einer Doppelfalle als Lösung vorgeschlagen. Dabei werden zwei Penningfallen
verwendet, die für die verschiedenen Messschritte besonders geeignet sind, und zwischen denen das Ion transportiert werden kann. Die erste Falle besitzt ein homogenes
Magnetfeld und wird zur Messung der Zyklotronfrequenz sowie zum Einstrahlen der
Larmorfrequenz verwendet. Sie wird als Präzisionsfalle bezeichnet. Die zweite Falle zeichnet sich durch das inhomogene Magnetfeld der magnetischen Falsche aus
und wird als Analysefalle bezeichnet. Hier wird die Spin-Einstellung aus der axialen
Frequenz detektiert. Der Abstand der beiden Fallen ist so dimensioniert, dass die
Auswirkungen der Inhomogenität der Analysefalle in der Präzisionsfalle kleiner sind
als die durch die Fallentechnik verursachten. Abbildung 2.8 gibt einen schematischen
Überblick über den Aufbau. Es wird dabei in der Präzisionsfalle ein B2 von etwa
µT
1 mm
2 erreicht und mithin
∆g
g
≈ 2 · 10−11 , womit die gewünschte Präzision erreichbar
ist.
Der gesamte Aufbau wird im Hochvakuum und bei einer Temperatur von etwa
4K betrieben. Damit ist es möglich, das Teilchen auf kleinen Bewegungsbahnen und
damit im harmonischen Bereich der Falle zu halten. Auch die erste Stufe der Nach-
18
2.5 Die Phasenmethode
Präzisionsfalle
Analysefalle
10 cm
Abbildung 2.8: Darstellung der Doppelfalle zur Ermittlung des g-Faktors. In der Präzisionsfalle links herrscht eine hohes, homogenes Magnetfeld zur genauen Messung der Bewegungsfrequenzen, in der Analysefalle rechts
wird eine magnetische Flasche zu Ermittlung der Spinorientierung
verwendet. Ganz rechts befindet sich ein Feldemissionsarray, mit dem
ein Elektronenstrahl erzeugt wird, der auf der gegenüberliegenden
Seite Atome aus dem Target löst und in der Präzisionsfalle ionisiert.
weiselektronik befindet sich in diesem kryogenen Bereich, was die den Betrieb von
Detektoren hoher Güte ermöglicht, um das Signal eines einzelnen Ions zu detektieren. Das Detektionsprinzip wird im folgenden Abschnitt genauer betrachtet. Eine
vollständige Beschreibung des Aufbaus inklusive der Kühlkomponenten findet sich
etwa in der Arbeit von Stefan Ulmer [Ulm11].
2.5 Die Phasenmethode
Wie oben beschrieben, dient die Analysefalle als Ausführung einer magnetischen Flasche dazu, die Spineinstellung des gefangenen Protons zu detektieren. Dies geschieht
über die Bestimmung der axialen Frequenz. Ist in der Präzisionsfalle durch Einstrahlen einer externen, auf den Spinflip abgestimmten Radio-Frequenz ein solcher
induziert worden, äußert sich dies in einer Veränderung der axialen Frequenz in der
Analysefalle. Bei der klassischen Methode, die absolute Frequenz aus einer FourierAnalyse des Signals zu extrahieren, benötigt jede dieser Messungen mindestens die
durch das Fourier-Limit bestimmte Zeit
tabs =
1
δνz
(2.30)
Im vorliegenden Experiment ist ein Frequenzunterscheid von δνz ≈ 250ms zu erwarten, womit sich für jede Messung eine Zeit von tabs = 4s ergibt.
19
2 Die Penningfalle
schneller
Spin down
langsamer
Phasendifferenz
Spin up
Abbildung 2.9: Veranschaulichung des Detektionsprinzips der Phasenmethode. Bei
gleicher Startphase ergibt sich bei unterschiedlicher Frequenz zweier
Schwingungen ein von der Wartezeit abhängiger Frequenzunterschied
δφ
Die hier beschriebene Phasenmethode setzt an dem Punkt an, dass nicht der Absolutwert der beiden Frequenzen benötigt wird, sondern lediglich der Unterschied
zwischen beiden. Die Methode wird in [Sta05] vorgestellt. Dabei vergleicht man die
Frequenzen zweier Schwingungen, die zu einem Zeitpunkt ohne Phasenunterschied
starten. Mit der Zeit entwickelt sich, abhängig vom tatsächlichen Frequenzunterschied, eine Phasendifferenz zwischen beiden Schwingungen:
δφ = 2πδνz tphase
(2.31)
mit der Wartezeit tphase (Abbildung 2.9). Über die Detektion des Phasenunterschieds
nach einer festgelegten Zeit lässt sich also auf den Frequenzunterschied schließen, wobei das oben beschriebene Fourier-Limit unterschritten werden kann. Im Experiment
wird dies realisiert, indem das Proton über eine Dipol-Anregung mit definierter Phase in Schwingung versetzt wird. Danach lässt man es die Zeit tphase frei schwingen.
Lässt sich nun ein Phasensprung nachweisen, hat ein Spinflip stattgefunden. Gegenüber der absoluten Frequenzmessung ergibt sich ein Zeitersparnisfaktor von
tphase
2π
=
tabs
δφ
(2.32)
der somit von der Möglichkeit abhängt, Phasenverschiebungen ab einer bestimmten
Größe klar bestimmen zu können. Der komplette Messablauf ist schematisch in Abbildung 2.10 dargestellt. In [Sta05] ergibt sich aus einer detektierbaren Phase von
ein Zeitersparnisfaktor 8.
20
π
4
2.5 Die Phasenmethode
Anregung
Phasendetektion
Elektrisches
Feld
Warten
Detektiertes
Signal
tAnr
tW
tDet
tKühl
Zeit
Abbildung 2.10: Schematische Darstellung des Messablaufs der Phasenmethode. Das
Teilchen startet nach externer Dipol-Anregung mit bekannter Phase, nach einiger Zeit wird der Phasenunterschied detektiert.
21
3 Die Detektionseinheit
Die oben beschriebenen Eigenfrequenzen des in der Falle gespeicherten Teilchens
müssen mit höchstmöglicher Präzision gemessen werden, um eine ebenso präzise Bestimmung des Wertes des g-Faktors zu erhalten. Betont werden soll hier noch einmal,
dass es sich um die Messung des Signals eines einzelnen einfach geladenen Ions handelt. Daher fällt dem Herausfiltern des Signals aus dem Untergrund eine sehr wichtige
Rolle zu, die Detektionssysteme müssen darauf abgestimmt sein. Das grundlegende
Prinzip der Signaldetektion sowie die experimentelle Ausführung werden im folgenden Kapitel beschrieben.
3.1 Grundlegendes Prinzip
Die Messung der Frequenz eines Teilchens in der Falle soll nicht-destruktiv erfolgen.
Das bedeutet, dass beim Durchführen einer Messung das Teilchen nicht verloren
geht. Herausgestellt werden muss dabei auch, dass somit alle Messungen über den
Zeitraum von Monaten tatsächlich an einem einzelnen Proton durchgeführt werden.
Die gewünschte Präzision ist nur erreichbar, wenn alle Messungen an einem einzelnen
Teilchen durchgeführt werden können.
Die hier verwendete Methode zur Messung nutzt die durch das Ion induzierten
Spiegelströme in den Fallenelektroden. Die Theorie dazu geht auf eine von Shockley bereits 1938 veröffentlichte Arbeit zurück, wonach die durch das Ion induzierten
Potentialunterschiede in einem leitenden Material direkt durch einen Stromfluss ausgeglichen werden [Sho38]. Darauf aufbauend entwickelte 1968 Dehmelt die „bolometrische“ Methode [Deh68], mit der die Frequenzen eines oszillierenden Teilchens in
der Penningfalle bestimmt werden kann.
Die induzierten Spiegelströme zeigen die selbe Zeitabhängigkeit wie die Bewegung
des Teilchens. In den Fallenelektroden fließt also ein Strom mit der gesuchten Frequenz. Über eine Impedanz kann dieser in ein Spannungssignal übersetzt werden,
das schließlich verstärkt und mittels Fourier-Transformation untersucht wird. Die
Herausforderung besteht darin, dieses Signal aus dem Untergrundrauschen heraus-
23
3 Die Detektionseinheit
zufiltern. Anhand der Detektion des Signals der axialen Bewegungsmode soll dies nun
veranschaulicht werden. Dazu vereinfacht man die beiden Endkappen zu unendlich
ausgedehnten Kondensatorplatten mit Abstand D. Der in ihnen induzierte Strom
ergibt sich einfach zu
Iind =
dQ
q
q
= ż = 2π νz z0
dt
D
D
(3.1)
mit der Ladung q und der Eigenfrequenz νz sowie Bewegungsamplitude Z0 , hier
bezogen auf die z-Koordinate der axialen Frequenz. Für die Detektion der Bewegung in der x-y-Ebene gilt die Gleichung mit dem Radius-Parameter ρ. In der realen
Penningfalle ist der Parameter D nicht einfach durch den Plattenabstand gegeben.
Er ergibt sich aus dem Teil der Oberflächenladung, welcher auf einer bestimmten
Elektrode induziert wird. Eine genaue Betrachtung ist in [Ulm11] gegeben. Der im
folgenden weiterhin als D bezeichnete effektive Elektrodenabstand ist ein Parameter
für die Ankopplung des Ionensignals an die Falle und wird durch die Elektrodengeometrie, aber auch durch das Design der Signalaufnahme beeinflusst. So führen
kleinere Elektrodenabstände als auch ein Abgriff des Signals an mehreren Stellen zu
einer Erhöhung der Ankopplung. Die für das Experiment ermittelten Werte werden
in Tabelle 3.1 angegeben.
Signalabgriff
Axial KE
Axial EK
Axial KE + EK
Zyklotron RE
Zyklotron EK
Zyklotron KE
Zyklotron KE + EK
Analysefalle
4,12 mm
4,53 mm
2,89 mm
-
Präzisionsfalle
7,60 mm
8,69 mm
5,58 mm
23,96 mm
15,59 mm
42,19 mm
14,23 mm
Tabelle 3.1: Überblick über die effektiven Elektrodenabstände in der Falle des
Proton-Experiments. Der Signalabgriff erfolgt an der Korrekturelektrode
(EK), Endkappe (EK), an beiden oder an der Ringelektrode (RE).
Die resultierenden Ströme liegen typischerweise im Bereich von 100 bis 200 fA.
Das Spannungssignal ergibt sich über die Multiplikation mit der Impedanz Z, an der
der Strom anliegt, zu
Uind = Iind · Z
(3.2)
Im einfachsten Fall, der bloßen Kapazität der Fallenelektroden, lässt sich daraus
24
3.1 Grundlegendes Prinzip
das Signal Uind =
−iz0 q
CD
mit der imaginären Einheit i, der Bewegungsamplitude z0
und der Fallenkapazität C. Die Amplitude beträgt also Uind =
z0 q
CD .
Eine Erhöhung
wäre durch eine Verringerung der Kapazität möglich, was im Design der Penningfalle allerdings nicht möglich ist. Typischerweise liegt der Wert hier bei etwa 10
pF. Dies ergibt eine Spannungsamplitude von etwa 3 nV. Auch eine Erhöhung der
Bewegungsamplitude verstärkt das Signal, jedoch überstreicht das Teilchen bei der
geforderten Größenordung dann auch anharmonische Potentialbereiche, womit die
gewünschte Präzision nicht erreicht werden kann. Abhilfe kann also nur eine Erhöhung der Gesamtimpedanz schaffen, über die der Strom anliegt. Erreicht wird dies
durch Parallelschalten einer Induktivität L, mithin entsteht ein Parallelschwingkreis.
Dies zeigt Abbildung 3.1 Das schlichte Parallelschalten eines hochohmigen Widerstands ist nicht möglich, da der Strom dann den Weg über die wesentlich geringere
Impedanz der Fallenkapazität wählt und am Widerstand nicht nachweisbar ist. Im
Parallelschingkreis dagegen heben sich auf der Resonanzfrequenz die Reaktanzen von
Kapazität und Induktivität auf, das Stromsignal liegt an einem hohen sich ergebenden effektiven Parallelwiderstand Ref f an. Diese Eigenschaften des Parallelschwingkreis werden im folgenden Abschnitt genauer geklärt.
Falle
mit
Teilchen
L
Falle
mit
Teilchen
C
Rp
C
L
RS
Abbildung 3.1: Skizze von Falle mit Nachweisschwingkreis: Der Nachweis besteht
aus einer Kapazität parallel zu einer Spule. Die ohmschen Anteile
sind zu einem Serienwiderstand RS in Reihe zur Spule dargestellt.
Für die weitere Behandlung erfolgt eine Transformation zu einem
Reihenschwingkreis mit Induktivität L, Kapazität C und effektivem
Parallelwiderstand Rp
25
3 Die Detektionseinheit
3.1.1 Der Parallelschwingkreis
Hier werden kurz die wesentlichen Eigenschaften eines Parallelschwingkreises eruiert,
wie er als Teil der Detektionseinheit des g-Faktor-Experiments auftritt. Vollständige
Beschreibungen finden sich in allen Standard-Lehrwerken zur Elektrotechnik.
Der Parallelschwingkreis besteht aus einer Kapazität C parallel zu einer Induktivität L. Die auftretenden ohmschen Anteile, sind im Verlustwiderstand RS gebündelt
dargestellt. Dabei handelt es sich um den endlichen Leitwert des Materials, Skinund Proximityeffekt [Sch03], Verluste im Resonatormaterial durch induzierte Spiegelströme und dielektrische Verluste im Isolationsmaterial [Men92]. Das Schaltbild
ist in Abb. 3.1 (links) dargestellt. Interessant ist die Gesamtimpedanz Z des Kreises
für eine Signalfrequenz ω. Sie ergibt sich zu
1
1
= iωC+
=
Z
iωL + RS
1
RS
+ 2 2
iωL ω L


1

1+
2
RS
2
ω L2
1
RS
+iωC ∼
= 2 2 +i ωC −
ω L
ωL
(3.3)
Für den letzten Schritt wurde die Näherung
2
RS
ω 2 L2
1 verwendet, was auf den Betrieb
des Resonators im kryogenen Bereich zutrifft. Hier sind die Ohmschen Anteile RS
gering. Um das Verhalten das effektiven Parallelwiderstands RP in Abbildung 3.1 zu
erhalten, betrachtet man dessen Gesamtimpedanz:
1
1
1
1
1
= iωC +
+
=
+ i ωC −
Z
iωL Rp
Rp
ωL
(3.4)
Der Imaginärteil beider Impedanzen ist identisch, weswegen die Kapazität und
Induktivität bei der Transformation unverändert bleibt. Für den Realteil und damit
den Ohmschen Anteil gilt dagegen
RS
1
= 2 2
Rp
ω L
(3.5)
Die Aufteilung in Real- und Imaginärteil ergibt die Resistanz und Reaktanz des
Resonators. Für die Verstärkung des Ionensignals ist der Betrag der Impedanz |Z|
maßgeblich:
|Z| = r
1
RL
ω 2 L2
2
+ ωC −
(3.6)
1 2
ωL
Übersichtlicher wird dies durch Verwendung der Resonanzfrequenz ω0 =
26
√1 ,
LC
die
3.1 Grundlegendes Prinzip
sich aus der Bedingung iωL =
1
iωC ,
also der Kompensation der Blindwiderstände
der imaginären Anteile, ergibt, sowie Einführung des Begriffs der Güte Q. Bei der
Güte handelt es sich um das Verhältnis von Blind- zu Wirkwleistung einer Schaltung.
Sie ist definiert als das Verhältnis von gespeicherter Energie zu Energieverlust pro
Schwingung.
Im[ Z1 ]
Q=
=
Re[ Z1 ]
1
ωC −
ωL
Rp ≈
Rp
ωL
=
ωL
RS
(3.7)
Die Approximation im vorletzten Schritt gilt für die Größenordnungen von Kapazität
(pF) und Induktivität (mH) bei der betrachteten Frequenz der axialen Schwingung
(ca. 700 kHz). Damit lässt sich |Z| formulieren zu
Rp
QωL
2 = r
2
2
2
1 + Q2 ωω2 − 1
1 + Q2 ωω2 − 1
|Z| = r
0
(3.8)
0
Maximale Impedanz und damit maximale Spannung ergibt sich bei ω = ω0 , Z ist
dann rein reell und gibt den gewünschten effektiven Parallelwiderstand Rp :
Z(ω = ω0 ) = Rp = Qω0 L =
ω02 L2
RL
(3.9)
Daraus lässt sich ableiten, wie der Resonator beschaffen sein muss, um über eine
hohe Impedanz ein hohes Spannungssignal auszugeben: Der Verlustwiderstand RS im
Resonator muss möglichst gering sein. Die Induktivität L sollte so hoch wie möglich
sein. Diese beiden Punkte entsprechen damit einer Maximierung der Güte Q. Gleichzeitig müssen aber Induktivität und Kapazität so aufeinander abgestimmt sein, dass
die Resonanzfrequenz des Schwingkreises mit der Eigenfrequenz der untersuchten
Bewegungsmode des Teilchens übereinstimmt.
Die oben beschriebene Güte Q wird auch in den weiteren Diskussionen eine wichtige Rolle spielen. Experimentell direkt zugänglich ist sie über die Darstellung der
Ausgangsspannung gegen die Frequenz. Dabei ist sie durch das Verhältnis der Resonanzfrequenz ν0 zur so genannten 3-dB-Breite ∆ν, siehe 3.2. Diese wiederum ist
für den Resonator definiert als Differenz der beiden Frequenzen, an denen die Transferfunktion auf den Faktor
√1
2
vom Maximalwert abgesunken ist. In logarithmischen
Einheiten entspricht dies einem Rückgang um 3 dB.
Q=
ν0
∆ν
(3.10)
27
3 Die Detektionseinheit
3 d B
S ig n a l
∆ν
ν0
F re q u e n z
Abbildung 3.2: Schematische Darstellung einer Resonanzkurve zur Ermittlung der
Güte Q aus der Resonanzfrequenz ν0 und der 3-dB-Breite ∆ν.
3.2 Das Teilchen als Reihenschwingkreis
In diesem Abschnitt wird das Verhalten des Teilchens in Bezug auf die Detektionsmethode diskutiert. Daraus ergeben sich zwei verschiedene Ansätze zur letztendlichen
Messung der Frequenz. Die Formulierung erfolgt für die Detektion der axialen Frequenz, ist aber vollständig äquivalent für die Detektion in der radialen Ebene.
Die Bewegungsgleichung für das Teilchen 2.5 in axialer Richtung muss um den Betrag der Wechselwirkung mit dem Nachweiskreis erweitert werden, die die Bewegung
von außen beeinflusst.
mz̈ = FΦ + Fext = −q∇Φ −
q
Uextern
D
(3.11)
Fext beschreibt das treibende Feld der Nachweiselektronik. Die gesamte Bewegungsgleichung lautet dann
mz̈ +
q2
C2 qU0
Rp ż +
z=0
D2
D2
(3.12)
Dies ist die Bewegungsgleichung eines gedämpften harmonischen Oszillators mit
Dämpfungskonstante
γ=
28
q 2 Rp
mD2
(3.13)
3.2 Das Teilchen als Reihenschwingkreis
und daraus resultierender Zeitkonstante
τ=
1
mD2
=
γ
Rp q 2
(3.14)
Setzt man die Beziehung zwischen Strom und Koordinaten Iind =
q
D ż
hier ein, ergibt
sich eine Differentialgleichung für den induzierten Strom
m
mωZ2 D2
D2 ˙
I
+
R
I
+
p ind
ind
q2
q2
Z
dtIind = 0
(3.15)
Vergleicht man dieses Verhalten mit der Differentialgleichung des Stroms in einem
Reihenschwingkreis
1
LI˙ + RI +
C
Z
dtI = 0
(3.16)
so lässt sich das Teilchen als Reihenschwingkreis mit den Parametern
LIon =
mD2
q2
(3.17)
RIon = Rp
CIon =
(3.18)
q2
mωZ2 D2
(3.19)
auffassen! Tatsächlich zeigt das Teilchen genau diese Eigenschaften in der Wechselwirkung mit der Detektionseinheit (Abbildung 3.3). Die Dämpfung kann durch die
Dissipation der Spiegelströme im effektiven Parallelwiderstand verstanden werden,
die dem Teilchen Energie entziehen.
RIon
Falle
mit
Teilchen
CIon
R
C
R
L
C
L
LIon
Abbildung 3.3: Schematische Darstellung des Detektionsprinzip. Das Teilchen kann
als Reihenschwingkreis mit Resonanzfrequenz ν0 aufgefasst werden,
der parallel zum Detektionskreis liegt.
29
3 Die Detektionseinheit
An dieser Stelle soll noch darauf hingewiesen werden, dass der effektive Parallelwiderstand Rp auch eine Auswirkung auf die Detektion nach der in 2.5 beschriebenen
Phasenmethode besitzt. Bei hohem Widerstand bewirkt die Dissipation von Schwingungsenergie im Nachweiskreis einen schnelleren Abfall der Schwingungsamplitude
des Teilchens. Bei der Phasenmethode muss aber diese hoch genug sein, um noch
einen Phasenunterschied zur anfänglichen Anregung auflösen zu können. Ideal wäre
es bei dieser Messung also, die Schwingung des Teilchens von der Detektionseinheit
zu entkoppeln. Dazu muss die Güte des Nachweiskreises künstlich stark erniedrigt
werden. Realisiert werden kann dies über einen „Güte-Schalter“, der den Parallelwiderstand in kurzer Zeit senken kann [Alo07].
3.3 Dip-Detektion
Die oben beschriebenen Eigenschaften des Teilchens in der Falle lassen sich zur zerstörungsfreien Messung der Bewegungsfrequenz im thermischen Gleichgewicht nutzen.
Das Teilchen agiert auf seiner Resonanzfrequenz, äquivalent zum Reihenschwingkreis,
als perfekter Kurzschluss. Auf dieser Frequenz kann also der Parallelschwingkreis der
Detektionseinheit überbrückt werden, es fällt keine Spannung darüber ab. Somit ergibt sich eine Delle, im Folgenden „Dip“ genannt, im Spektrum. Dieses setzt sich
zusammen aus dem thermischen Spannungsrauschen und dem Stromrauschen, das
über den effektiven Parallelwiderstand ebenfalls als Spannungsrauschen zu sehen ist.
Die Herkunft dieser Beiträge wird im Kapitel 4.2 genauer beleuchtet. Für ein eingehenderes Verständnis betrachten wir den Realteil der Transferfunktion eines zum
Effektivwiderstand Rp parallel geschalteten Reihenschwingkreis, eben dem Teilchen
selbst:
Re(Z) =
1
ωCIon
Rp ωLIon −
Rp2 + ωLIon −
2
1
ωCIon
2
Unter Verwendung der Resonanzfrequenz des Reihenschwingkreises ω0 =
(3.20)
1
,
(LIon CIon )2
der Bewegungsfrequenz des Teilchens, ergibt sich damit
Re(Z) =
1+
Rp
Rp2
ω02 L2Ion
ωω0
ω 2 −ω02
2
(3.21)
Daraus kann abgelesen werden, dass der Realteil bei Resonanz verschwindet. Stromrauschen dieser Frequenz wird also nicht als Spannung am Detektor sichtbar. Weit
30
3.3 Dip-Detektion
von der Resonanzfrequenz entfernt verschwindet der quadratische Term und das
System aus Teilchen und Detektionsresonator ist wieder durch den effektiven Parallelwiderstand des Resonators Rp allein gegeben.
Damit der Dip im Stromrauschen überhaupt sichtbar ist, muss dieser natürlich
wesentlich schmalbandiger sein als die Transferfunktion des Resonators. Die 3-dBBreite des Dips ist analog zu der des Resonators gegeben durch
∆ν =
ν0
1 1
1 q 2 Rp
1 Rp
=
=
=
2
Q
2π τ
2π mD
2π LIon
(3.22)
und liegt auf Grund der hohen äquivalenten Induktivität des Teilchens Größenordnungen unter der des Nachweisschingkreises. Dieser erreicht Güten Q im Bereich von
10 000, während das Teilchen eine Güte von etwa 1 000 000 errreicht. Andererseits
darf die Breite des Dips nicht zu gering sein, da seine Lage mit den zu Beginn erwähnten Fluktuationen in den Fallenfeldern variieren kann. Eine Dipbreite, die unter
der Größenordnung der Fluktuationen liegt, führt dazu, dass bei der Mittelung über
viele Messungen der Dip im Spektrum „ausgewaschen“ wird. Für eine Verbreiterung
des Dips ist ein möglichst großer effektiver Parallelwiderstand des Nachweiskreises
Rp vonnöten.
Ein weiterer wichtiger Parameter zur Auflösung des Dips ist das Signal-zu-RauschVerhältnis (signal-to-noise ratio, SNR). Es gibt eine Kennzahl zur Qualität des gesamten Detektionssystem. Es beschreibt das Verhältnis des zur Untersuchung genutzten Signals zum Untergrundrauschen.
Uein
SN R = qP
(3.23)
2
k ek
Dabei ist Uein eben das Eingangssignal und die ek die Beiträge durch verschiedene Rauschquellen (für eine eingehende Betrachtung des Rauschens in elektronischen
Schaltungen siehe Kapitel 4.2). Da sie als stochastische Ereignisse unkorreliert sind,
werden sie quadratisch addiert. Im Falle des hier betrachteten Nachweiskreises handelt es sich um thermisches Rauschen nach dem Johnsons-Nyquist-Theorem [Joh]
[Nyq] (eine genauere Beschreibung findet sich bei der Eruierung dieser Phänomene
in Bezug auf den Verstärker) und durch die aktiven elektronischen Bauteile erzeugtes Rauschen [Jef93]. In 3.4 ist eine Aufschlüsselung der wichtigen Kennparameter
gegeben.
Um ein hohes SNR zu erreichen, muss der Aufbau des Detektionsprinzip und
die Beiträge der einzelnen Rauschquellen genau untersucht werden. Einen solchen
31
3 Die Detektionseinheit
S ig n a l
3 d B
∆ν
S N R
ν0
F re q u e n z
Abbildung 3.4: Schematische Darstellung des Dips. Der Dip entsteht durch einen
Kurzschluss des effektiven Parallelwiderstands des Nachweisschwingkreises. Zu sehen ist die Dipbreite ∆ν und das Signal-zu-RauschVerhältnis SN R. Im realen Experiment ist der Dip sehr viel schmaler.
Überblick gibt Abbildung 3.5
Das Teilchen ist durch die Stromquelle IIon dargestellt. Der Nachweisschwingkreis
liegt parallel zur Falle. Über einen Koppelkondensator Cc wird der Verstärker angeschlossen. Dieser ist modelliert als idealer Verstärker, an dessen Eingang parallel
eine Eingangskapazität Cin und ein Eingangswiderstand Rin auftritt (eine genauere
Betrachtung wird bei der Diskussion des Verstärker gegeben). Am Eingang des Verstärkers ist dessen Rauschen in das Spannungsrauschen en und das Stromrauschen
in aufgeteilt.
Um das Signal-zu-Rausch-Verhältnis bei der Dip-Methode zu berechnen, benötigt man den Abstand des Untergrundrauschens, dass durch das Eingangsrauschen
en des Verstärkers selbst gegeben ist, zu der Amplitude der Spannung bei der Resonanzfrequenz des Nachweisschwingkreises. Diese setzt sich aus dem thermischen
Rauschen eth des effektiven Resonanzwiderstandes, dem durch das Stromrauschen
in verursachten Spannungabfall an eben diesem Widerstand und ebenfalls dem Eingangsrauschen zusammen. Nun muss noch der Einfluss der Kopplung des Verstärkers
an den Schwingkreis betrachtet werden. Die Koppelkapazität Cc und die unvermeidliche Eingangskapazität Cin des Kondensators bilden einen Spannungsteiler, der zwei
Effekte hat: Zum einen liegt nur ein Teil des Signals des Resonators tatsächlich am
Eingang des Verstärkers an, zum anderen wirkt der parallel geschaltete Eingangswi-
32
3.3 Dip-Detektion
Ion in der
Falle
Detektionskreis
Kompletter Verstärker
idealer
Verstärker
en
CC
IIon
CFalle
Rp
Cp
Lp
in
Cin
Rin
Abbildung 3.5: Schematische Darstellung der kompletten Detektionselektronik. Eingangswiderstand und -kapazität des Verstärkers haben einen wesentlichen Einfluss auf die Dipbreite und das SNR
derstand Rin des Verstärkers nur teilweise auf den effektiven Parallelwiderstand des
Parallelschwingkreises. Das Parallelschalten dieses Widerstands bewirkt ein Absinken des effektiven gesamten Systemwiderstands Rsys . Für diesen gilt
Rsys =
Cc + Cin
Cc
2
Rp +
Rp Rin
2
Cc +Cin
Cc
(3.24)
Rin
Mit der Einführung des Kopplungsfaktor
α=
Cc
Cc + Cin
(3.25)
(harte Ankopplung bedeutet dann einen Faktor nahe 1) ergibt sich dies zu
Rsys =
Rp Rin
1
2
α Rp + α12 Rin
(3.26)
Damit können die einzelnen Beiträge errechnet werden. Das thermische Rauschen
p
des Systemwiderstands ist eth = 4kB T Rsys ∆ν mit Boltzmann-Konstante kB , Temperatur T und Bandbreite ∆ν, über der das Rauschen gemessen wird. Das Stromrauschen in ist um den Faktor α2 verringert und trägt mit in Rsys α2 bei. Das Eingangsspannungsrauschen des Verstärkers bleibt unverändert. Es gilt
33
3 Die Detektionseinheit
q
SN RDip =
e2th + (in Rsys α2 )2 + e2n
en
(3.27)
beziehungsweise
s
SN RDip =
2 i2 α 4 + e2
4kT Rsys + Rsys
n
n
e2n
(3.28)
und damit schlussendlich
SN RDip
v
u
2
u
α2 R p
α2 R p
u 4kT
+
i2n α4 + e2n
R
R
u
1+α2 R p
1+α2 R p
t
in
in
=
e2n
(3.29)
Dieser Ausdruck beinhaltet den Einfluss der Verringerung des effektiven Parallelwiderstands Rp des Nachweiskreises durch einen geringeren Eingangswiderstand des
Verstärkers sowie die Tatsache, dass bei weicherer Ankopplung ein geringerer Anteil des Signals transferiert wird. Für experimentell ermittelte Werte kann daher der
Kopplungsfaktor innerhalb bestimmter Grenzen so angepasst werden, dass sowohl
ein möglichst hohes SNR als auch eine möglichst große Dipbreite erreicht werden
können.
3.4 Peak-Detektion
Eine Alternative zur Dip-Detektion bietet die Anregung der entsprechenden Mode
durch äußere Dipol-Strahlung, also eine angepasste treibende Spannung. Wird das
Teilchen über die physikalische Temperatur des Nachweiskreises erhitzt, dissipiert
es Energie in diesen. Im Rauschspektrum ist dies als Peak auf der Resonanzkurve, vgl. 3.6. Diese Methode hat den Nachteil, das größere Raumbereiche der Falle
überstrichen werden und Inhomogenitäten in den Feldern stärker zum Tragen kommen. Die Vorteile sind, dass im Prinzip, bei Beachtung der Inhomogenitäten, hohe
Signalstärken erzeugt werden können. Außerdem wird hier im Gegensatz zum Dip
die tatsächliche Schwingung des Teilchens detektiert, womit die Phasenmethode Anwendung finden kann (Kapitel 2.5).
Für diese Art der Detektion muss das Signal-zu-Rausch-Verhältnis anders definiert
werden, wie in Abbildung 3.6 dargestellt. Das Nutzsignal ist nun der durch das
Teilchen induzierte Strom IIon , der am Effektivwiderstand Rp als Spannung abfällt:
34
3.4 Peak-Detektion
S ig n a l
S N R
ν0
F re q u e n z
Abbildung 3.6: Schematische Darstellung des Signals zur Detektion über die PeakMethode. Das Signal-Rausch-Verhältnis ist eingezeichnet
UIon = IIon Rp = IIon 2πνQL
(3.30)
Dies ist in Verhältnis zu setzen zum Rauschen, das aus der quadratischen Addition
von wieder thermischen Rauschen, dem (teilweise abgekoppelten) Stromrauschen und
dem Eingangsrauschen des Verstärkers besteht:
e2tot = e2n + 4kT Rsys α2 + (in Rsys )2 α4
(3.31)
Es ergibt sich unter Berücksichtigung der Abkopplung und Verringerung des Resonanzwiderstands:
SN RP2 eak =
(IIon Rsys )2 α2
(IIon Rsys )2 α2
=
e2tot
e2n + 4kT Rsys α2 + (in Rsys )2 α4
(3.32)
35
3 Die Detektionseinheit
und damit schlussendlich
(IIon Rin Rp )2
#
2
i
R
R
4kT
R
R
in
in p
e2n + n pRin
+
Rp +
Rin
SN RP2 eak = "
Rp +
α2
Rp +
α2
(3.33)
Rin
α2
2
α2
Das SN RP eak hat ein Extremum für einen bestimmten Kopplungsfaktor, wie sich
für gegebene Ausgangsparameter grafisch ermitteln lässt. Außerdem ist das SNR
natürlich von der Stärke des Ionensignals abhängig. Typischerweise liegt dies im
Bereich von 100 fA.
3.5 Anforderungen an das Detektionssystem
Aus den oben ermittelten Formeln für das Signal-zu-Rausch-Verhältnis sowie der
Breite des Dips lassen sich die grundlegenden Anforderungen an das Detektionssystem zusammenfassen:
• Der Parallelschwingkreis, der die Impedanz liefert, an der das Ionensignal abfällt, sollte auf maximalen effektiven Parallelwiderstand Rp und damit maximalen Gütefaktor Q optimiert werden. Dafür eignen sich Spulen mit einer hoher
Induktivität.
• Der Verstärker sollte einen hohen Eingangswiderstand Rin besitzen, um den
Nachweisschwingkreis möglichst wenig zu bedämpfen.
• Das Eingangsspannungsrauschen en minimiert sollte minimiert werden, da es
bei beiden Messmethoden in das Untergrundrauschen eingeht.
• Das Eingangsstromrauschen in bewirkt bei der Dip-Methode einen Anstieg der
Höhe der Resonanzkurve, da es über den effektiven Parallelwiderstand Rp als
Spannungssignal vorliegt. Damit erhöht es das SNR. Bei der Peak-Methode
geht es skalierend mit Rp in den Untergrund ein.
• Das System sollte im kryogenen Bereich betrieben werden, da hier thermisches
Rauschen verringert werden kann. Auch können supraleitende Materialien eingesetzt werden, um einen niedrigen Serienwiderstand RS zu erreichen.
Im Abschnitt 4 wird der Aufbau und die Charakterisierung eines Verstärkers beschrieben, der im Zusammenspiel mit dem Detektionskreis diese Anforderungen er-
36
3.5 Anforderungen an das Detektionssystem
füllen soll. Besonders wichtig sind dabei der Eingangswiderstand und das Eingangsrauschen.
37
4 Der kryogene Verstärker
In diesem Kapitel wird der Aufbau und die Untersuchung des kryogenen Verstärkers
beschrieben. Zunächst erfolgt eine Erklärung der Grundlagen, danach werden die
experimentellen Ergebnisse präsentiert und zum Schluss die Eigung für das ProtonExperiment eruiert.
4.1 Feldeffekt-Transistoren (FETs)
In kryogener Umgebung können im Allgemeinen keine Standard-Operationsverstärker
eingesetzt werden, da die verbauten Transistoren mit Si-Halbleitern im Allgemeinen nicht kryotauglich sind. Silizium besitzt eine Ionisierungsenergie von etwa 40
meV [Dem00]. Die Funktionstüchtigkeit unterhalb etwa 100K ist damit stark eingeschränkt, man spricht vom „Ausfrieren“ der Ladungsträger. GaAs-Halbleiter können
auf Grund ihrer hohen Donatorenkonzentration und einer geringen Ionisierungsenergie dagegen noch bei Temperaturen von 4K betrieben werden. Für den untersuchten Verstärker kommen GaAs-MESFETs zum Einsatz. MESFET steht für metal
semiconductor field effect transistor, also Matell-Halbleiter-Feldeffekttransistor. Die
Funktionsweise von Feldeffekttransistoren im Allgemeinen und MESFETs im Besonderen kann in jedem Elektronik-Lehrbuch gefunden werden, etwa in [Hil89]. Hier
wird ein kurzer Überblick über die Funktion als auch über die für das Experiment
wichtigen Eigenschaften gegeben.
Abbildung 4.1 zeigt den schematischen Aufbau eines n-Kanal-MESFETs. Die Anschlüsse Source, Gate und Drain entsprechen den Anschlüssen Emitter, Basis und
Kollektor bei bipolaren Transistoren. Bei FETs generell wird der Drainstrom zwischen Drain und Source über die (negative bei n-Kanal-FETs) Gate-Source-Spannung
reguliert. Beim MESFET liegt die Gate-Spannung über einen Metall-HalbleiterÜbergang, einen sogenannten Schottky-Kontakt, an. Im Transistor bildet sich je nach
anliegender Gate-Spannung eine Sperrschicht veränderlicher Größe, die nicht mehr
zur Leitung zwischen Source und Drain zur Verfügung steht. Ab einer bestimmten
Abschnürspannung fließt kein Strom mehr, ohne anliegende Spannung am Gate ist
39
4 Der kryogene Verstärker
IDrain
Drain
UDS
Gate
Gate
n-dotiert
UGS
Sperrschicht
Source
Abbildung 4.1: Schematische Darstellung der Funktionsweise eines n-KanalMESFETs. Die an den Gate-Anschlüssen anliegende negative Spannung variiert die Größe der Sperrzone, die nicht zur Leitung zwischen Drain und Source zur Verfügung steht. Damit variiert sich der
Drainstrom.
der FET leitend. Die natürliche Beschreibung der Wirkung des FETs erfolgt über
die sogenannte Steilheit
gm =
∂IDrain
iDrain
=
∂UGS
uGS
(4.1)
also der Änderung des Drainstroms bei Variation der Gate-Source-Spannung. Kleine Buchstaben werden dabei verwendet um klar zu machen, dass es sich um Änderungen in kleinen Spannungsbereichen handelt. Die Steilheit besitzt unterschiedliche
Werte für unterschiedliche Gate-Spannungen zwischen 0V und der Abschnürspannung. Über eine Gleichspannungsquelle kann demnach der Arbeitspunkt des FETs
angesteuert werden.
Ein Hauptunterschied zwischen FETs und Bipolartransistoren ist also, dass bei
FETs quasi kein Strom zwischen Gate und Source fließt, was einen nahezu leistungslosen Betrieb erlaubt und hochohmige Eingangswiderstände im Bereich bis zu 100
MΩ liefert. Der Schottky-Kontakt anstelle eines pn-Übergangs bewirkt eine im Vergleich niedrigere Eingangskapazität [Mar07].
40
4.1 Feldeffekt-Transistoren (FETs)
4.1.1 FET-Grundschaltungen
Beim Aufbau des Verstäkers werden die oben vorgestellten MESFETs zu verschiedenen Zwecken eingesetzt. Eine Übersicht über die verschiedenen Schaltungen ist
wiederum in jedem Elektronik-Lehrbuch (z.B. [Hil89]) zu finden und wird hier kurz
angerissen. Abbildung 4.2 zeigt die drei Grundschaltungen. Die Schaltungen sind
benannt nach dem Anschluss, der den gemeinsamen Spannungsbezugspunkt bildet.
Gate
Rwork
Rwork
Rwork
Drain
Uaus
Uaus
Uein
Uein
Source
Drain
Source
Source
Gate
Uein
Gate
Uaus
Drain
Abbildung 4.2: Die drei Transistor-Grundschaltungen anhand von Dual-GateMESFETs. Links die Sourceschaltung, in der Mitte die Drainschaltung bzw. Sourcefolger, rechts die Gateschaltung.
Die Sourceschaltung ist die verbreitetste Ausführung und wird zur Spannungsverstärkung von Signalen verwendet. Gemäß der oben definierten Steilheit gm ergibt
sich die Verstärkung, die durch den Arbeitswiderstand Rwork steuerbar ist, zu
GSpannung =
uD
iD
= −Rwork
= −gm Rwork
uGS
uGS
(4.2)
Sie bietet in der Ausführung eines FET einen hohen Eingangswiderstand und einen
hohen Ausgangswiderstand.
Der Sourcefolger (bzw. die Drainschaltung) wird zur Impedanzwandlung verwendet. gemäß ihrer Auslegung bietet sie keine Spannungsverstärkung, es gilt
und damit
uS = Rwork iD = Rwork gm uGS = Rwork gm (uG − uS )
(4.3)
Rwork · gm
ug
uS =
(1 + Rwork · gm
(4.4)
Damit erreicht der Sourcefolger für genügend großes Rwork (Rwork 1/gm ) eine
Spannungsverstärkung nahe 1, bleibt jedoch stets darunter. Gleichung 4.4 kann verstanden werden, indem man sich den Ausgangswiderstand des Sourcefolgers mit dem
Wert 1/gm vorstellt. Für FETs sind damit Ausgangswiderstände im Bereich weni-
41
4 Der kryogene Verstärker
ger 100 Ω realisierbar, der Sourcefolger wandelt also eine hohe Eingangsimpedanz,
wie sie etwa von vorangegangenen Sourceschaltungen herrührt, in eine niedrigere
Ausgangsimpedanz, an die weitere elektronische Schaltungen angeschlossen werden
können.
Die Drainschaltung besitzt als einzelnes Bauelement nur eine Bedeutung in der
Hochfrequenztechnik. Beim vorliegenden Verstärkerdesign spielt sie jedoch eine Rolle
als zweite Stufe einer Kaskode. Die Kaskodenschaltung ist in Abbildung 4.3 dargestellt.
Rwork
Gate
Drain
Uaus
UGate 2
Source
Gate
Uein
Drain
Source
Abbildung 4.3: Schematische Darstellung der Kaskodenschaltung mit Dual-GateMESFETs. Auf einen FET in Sourceschaltung folgt ein zweiter FET
in Gateschaltung. Die Schaltung verrgingert die Rückkopplung des
verstärkten Ausgangsspannungssignals auf den Eingang.
Der Zweck der Kaskodenschaltung ist die Verringerung der Rückkopplung des
verstärkten Ausgangsspannungssignal auf den Signaleingang. Diese Rückkopplung
über eine immer vorhandene kapazitive Kopplung zwischen Gate und Drain CGD ist
der sogenannte Miller-Effekt. Er bewirkt eine Vergrößerung der Eingangskapazität
an einem invertierenden Verstärker [Mil12], wie er hier vorliegt. Am Drainanschluss
einer gewöhnlichen Sourceschaltung liegt eine um den Verstärkungsfaktor größere
Spannungsamplitude als am Eingang an, die über die Millerkapazität auf den Eingang
zurückwirkt.
42
4.2 Rauschen
Der obere FET in der Abbildung liegt zwischen dem Drain-Anschluss des FETs in
Sourceschaltung und dem Arbeitswiderstand Rwork . Er ist in Gateschaltung installiert. Der Source-Anschluss bietet effektiv einen niedrigen Eingangswiderstand, wodurch eine nur geringe Spannungsverstärkung des ersten FETs entsteht, der über die
Gate-Drain-Spannung den Drainstrom steuert. Der untere FET steuert den oberen
in dem Sinne an, dass er dessen Gate-Drain-Spannung reguliert. Der obere FET reagiert darauf mit einem angepassten Stromfluss, ohne große Spannungsschwankungen
am seinem Source-Anschluss zu bewirken. Durch die geringere Spannungsamplitude
wird der Millereffekt stark reduziert. Am Arbeitswiderstand Rwork am Drain des
oberen FETs kann das verstärkte Spannungssignal abgegriffen werden.
4.2 Rauschen
Die Verstärkerstufe wird mit Hinblick auf ein hohes Signal-Rausch-Verhältnis konzipiert. Dabei ist das Eingangsrauschen des Verstärkers eine zentrale Kennziffer. Ein
möglichst geringes Eingangsspannungsrauschen bedeutet, dass sich das untersuchte
Signal deutlicher vom Rauschuntergrund abhebt. Eine Motivation für die Charakterisierung der hier beschriebenen Verstärkerstufe ist die Verbesserung des bisherigen
Verstärkers zur Untersuchung der axialen Frequenz. Dieser hat ein Eingangrauschen
√
von 1,6 nV/ Hz bei einer Frequenz von 600 kHz.
In einer elektronischen Schaltung addieren sich die einzelnen Rauschbeiträge der
Komponenten zum Gesamtrauschen. Demnach müssen die verschiedenen Rauschquellen innerhalb des Systems identifiziert und quantifiziert werden, um eine effektive Reduktion des Gesamtrauschens zu erreichen. Grundsätzlich müssen dabei unterschiedliche Mechanismen der Rauschentwicklung unterschieden werden. Zugang dazu
findet man über das Modell eines leitenden Stabes der Länge l, in dem der Strom I
durch n Ladungsträger mit der Elementarladung e und konstanter Geschwindigkeit
v gegeben ist [Spi06]:
I=
ne
env
=
t
l
(4.5)
Die Schwankungen des Stromes ergeben sich durch Schwankungen in aktueller
Geschwindigkeit und Anzahl der Ladungsträger zu
(dI)2 =
en
l
dv
2
+
ev
l
dn
2
(4.6)
Die Geschwindigkeitsänderungen der Ladungsträger im ersten Term sind ther-
43
4 Der kryogene Verstärker
misch bedingt. Diese Art von Rauschen, das thermische Spannungsrauschen, wurde
1928 von Johnson experimentell und von Nyquist parallel theoretisch untersucht
und beschrieben [Joh] [Nyq]. Die Stromschwankungen sind an einem Widerstand als
Spannungssschwankungen sichtbar, es gilt
Irausch,therm = in =
p
f kB T ∆ν/R
(4.7)
p
f kB T ∆νR
(4.8)
bzw.
Urausch,therm = en =
Dabei bezeichnet ∆ν die Breite des Frequenzbandes, in dem das Rauschen beobachtet wird. Zur Untersuchung dieser Rauschquelle in elektronischen Systemen kann
wie in Abbildung 4.4 ein rauschender Widerstand modelliert werden, indem eine
Spannungsrauschquelle en in Reihe zu einem idealen, also rauschfreien Widerstand
gleicher Größe geschaltet wird [Ste03].
Rrauschfrei
Rrausch
en
Abbildung 4.4: Ersatzschaltung eines rauschenden Widerstandes. Der rauschende
Widerstand wird durch einen rauschfreien Widerstand in Reihe zu
einer Rauschspannungsquelle en modelliert.
Die Leistung P , die diese Ersatzschaltung an einen idealen Lastwiderstand RL
abgeben kann, erhält man über
P =
RL
RL R
e2 =
4kB T ∆ν
R + RL n (R + RL )2
(4.9)
Bei Impedanzanpassung R = RL erhält man die maximal übertragbare Leistung
Pmax = kT ∆ν
(4.10)
Die Leistung ist also nicht abhängig von der Größe des rauschenden Widerstan-
44
4.2 Rauschen
des. Außerdem ist es nicht von der Frequenz abhängig, besitzt also eine konstante
spektrale Leistungsdichte. Ein Rauschsignal dieser Charakteristik bezeichnet man als
„weißes“ Rauschen.
Der zweite Term in Gleichung 4.6 ist auf die Schwankungen der Anzahl der Ladungsträger zurückzuführen. Hierbei sind zwei Ursachen zu unterscheiden. Das ebenfalls „weiße“ Schrotrauschen resultiert aus der Quantelung der Ladungsträger [Sch26].
Bei Überschreiten einer Potentialbarriere fließt ein Strom I0 nicht gleichmäßig, sondern die einzelnen Ladungsträger überwinden die Barriere stochastisch verteilt. Es
ergibt sich ein vom fließenden Strom abhängiges Stromrauschen
Ischrot =
p
2eI0 ∆ν
(4.11)
Der zweite Beitrag zum Rauschen auf Grund von Schwankungen der Ladungsträgeranzahl ist in einem GaAs-MESFET gegeben durch Fehler in der Gitterstruktur
der Halbleiter sowie einen Anteil, der von der Oberflächenstruktur abhängt [Fol86].
Die spektrale Leistungsdichte dieses Anteils nimmt mit ansteigender Frequenz ab.
Ein Rauschen mit dieser 1/ν-Charakteristik wird als „1/f-Rauschen“ oder auch „rosa“ Rauschen bezeichnet.
Um das Rauschen durch eine Messvorrichtung zu quantifizieren, betrachtet man
die zeitliche Entwicklung des stochastischen Spannungssignals. Dabei treten durch
das Rauschen kurzzeitige Amplituden auf, die statistisch verteilt positiv oder negativ sein können. Der lineare Mittelwert beträgt jedoch stets 0, da auf Grund von
Rauschen keine effektiven Ströme zwischen zwei Punkten fließen können [Tex01].
Die Amplituden der Schwankungen gehorchen einer Standard-Gaußverteilung. Deren Standardabweichung σ liefert den sogenannten RMS-Wert (root mean square =
quadratischer Mittelwert), einen „Effektivwert“ zur Quantifizierung der Rauschleistung.
Um eine Abschätzung der Beiträge einzelner Komponenten der gesamten Verstärkerelektronik zu erhalten, ist das Rauschmaß N F (noise figure) eine hilfreiche Größe.
Das in Kapitel 3.3 definierte Signal-Rausch-Verhältnis SNR lässt sich anschaulich
auch als folgendes Verhältnis betrachten:
SN R =
Saus
A · Sein
=
Sein
A · Nein + NAmp
(4.12)
Dabei ist Sein die in den Verstärker gelandende Signalstärke und Nein die beiliegende Rauschleistung. Beides wird mit dem Leistungsverstärkungsfaktor A verstärkt.
Ferner wird die durch den Verstärker zugefügte Rauschleistung NAmp einbezogen. Zur
45
4 Der kryogene Verstärker
Charakterisierung einer Komponente ist also ein Maß der zugefügten Rauschleistung
nötig, die Rauschzahl F mit
F =
NAmp
Naus
Sein Saus
/
=
=1+
Nein Naus
A · Nein
A · Nein
(4.13)
Sie gibt damit an, um wie viel sich das Verhältnis von Signal und Rauschen nach
dem Verstärker verschlechtert. Ein ideales, nicht rauschendes Bauteil hat somit eine
Rauschzahl von F = 1. Häufig wird auch das in dB ausgedrückte Rauschmaß NF
= 10 log F verwendet. Mit diesen Werten kann die Auswirkung der Rauschbeiträge
mehrerer Komponenten in einer elektronischen Signalkette untersucht werden. Die
Friissche Formel [Fri44] liefert als Gesamtrauschen nach k Komponenten
Fk = F1 +
F2 − 1 F3 − 1
Fk − 1
+
+ ... +
A1
A1 A2
A1 A2 ...Ak−1
(4.14)
Die Rauschzahlen der nach der ersten Verstärkerstufe liegenden Komponenten F2 ,
F3 usw. sind also jeweils um die das Produkt der Verstärkung der vorliegenden Stufen
unterdrückt. Insbesondere lässt sich das Gesamtrauschen der Kette bei geschicktem
Aufbau im Wesentlichen durch das Rauschen der ersten Stufe bestimmen. Dazu
muss die Verstärkung dieser Stufe ausreichend hoch sein, was neben dem geringen
Rauschen eine weitere Anforderung an den untersuchten Verstärker ergibt.
Dieser Verstärker wird, wie bereits im Kapitel 3.3 angedeutet, durch eine Stromrauschquelle in und eine Spannungsrauschquelle en am Eingang des dann als rauschfrei angenommenen idealen Verstärkers modelliert. Das Spannungsrauschen ist dabei
im Wesentlichen durch thermisches Rauschen und 1/f-Rauschen gegeben, das Stromrauschen findet in der Drain-Source-Strecke des MESFETs statt [Lee89]. Es ist zu
beachten, dass eine genaue Identifizierung der einzelnen physikalischen Abläufe, die
zum Rauschen beitragen, nicht immer möglich ist. Jedoch reicht eine Quantifizierung des Gesamtrauschens des Verstärkers, um eine vollständige Charakterisierung
zu erhalten.
Abbildung 4.5 zeigt das äquivalente Schaltbild, wobei noch eine Spannungsquelle
U0 , die das Nutzsignal repräsentiert, mit Innenwiderstand R0 vorgeschaltet ist. Für
die Rauschzahl gilt
F =1+
e2n
R0
+ i2n R0
4kB T ∆ν
(4.15)
Die Rauschzahl, wie auch das Signal-Rausch-Verhältnis, hängen also neben den intrinsischen Rauschparametern en und in von dem Eingangswiderstand R0 an. Aller-
46
4.2 Rauschen
Kompletter Verstärker
R0
etherm
U0
en
idealer
Verstärker
in
Abbildung 4.5: Schematische Darstellung zu internen Rauschquellen des Verstärkers.
Die internen Rauschquellen des Verstärkers werden durch eine Stromquelle in und eine Spannungsquelle un modelliert. Ein vorgeschalteter Widerstand
R0 trägt noch mit seinem thermischen Rauschen
√
etherm = 4kB T R0 ∆ν zum Gesamtrauschen bei.
dings ist sie unabghängig von der Verstärkung. Ein Minimum der Rauschzahl erhält
man durch Impedanzanpassung des vorhergehenden Ausgangswiderstands, im Falle
des vorliegenden Detektionsnachweises, indem der Parallelwiderstand des Resonanzschwingkreises über eine kapazitive Kopplung mit Kopplungsfaktor α =
CC
CC +Cin
aus
Gleichung 3.25 transformiert wird, wie in Kapitel 3.3 beschrieben. Man erhält
Roptimal =
en
in
(4.16)
Mit der Stärke der Abkopplung ändert sich allerdings auch das Signal-RauschVerhältnis, wie in Abschnitt 3.3 dargestellt. Da das SNR die maßgebliche Kennzahl
des Verstärkers ist, muss die Transformation in Hinblick auf optimales SNR und
nicht auf optimales Rauschmaß optimiert werden. Das Rauschmaß ist somit nur in
Bezug auf die Eingangsimpedanz anzugeben, womit es sich als unabhängige Kennzahl
des Verstärkers selbst nur bedingt eignet. Unkritisch sind hingegen die intrinsischen
Größen en und in , um die Rauscheigenschaften des Verstärkers vollständig zu beschreiben. Der intrinsische Eingangswiderstand sowie die Eingangskapazität müssen
dann noch separat ermittelt werden.
Eine Größe, die sich zur Charakterisierung des Rauschens insgesamt eignet, ist die
Rauschtemperatur, die angibt, welche Temperatur der rauschende Quellwiderstand
haben müsste, damit dessen thermische Rauschleistung mit der Gesamtrauschleistung des Verstärkers übereinstimmt
q
p
e2 + i2n R02
4kB T R0 = e2n + i2n R02 ⇔ T = n
4kB R0
(4.17)
47
4 Der kryogene Verstärker
Bei Impedanzanpassung vereinfacht sich dies zu
T =
en in
2kB
(4.18)
Die Bedeutung der Rauschtemperatur lässt sich veranschaulichen, indem man sie
mit der realen physikalischen Temperatur des Nachweiskreises vergleicht. Der Einfluss
des Rauschens ist klein, wenn die Rauschtemperatur deutlich unter dieser realen
Temperatur liegt.
4.3 Parasitäres Feedback
Um das Verhalten des Verstärkers im Eingangsbereich genauer zu verstehen, insbesondere die Eingangskapazität und den Eingangswiderstand, kann der Feedbackmechanismus einer Lastimpedanz auf den Eingang untersucht werden. Dazu verwendet man ein vereinfachtes Modell eines FETs, bei dem der Eingang, also das Gate,
über die sogenannte Miller-Kapazität mit dem Drain verbunden ist [Ulm11]. Der
Drain wiederum besitzt den Drain-Source-Widerstand RDS gegen Masse (Source)
und außerdem die Steilheit gm als Maß der Drainstromänderung bei Änderung der
Gate-Source-Spannung. Diese liegt parallel zu RDS .
Drain
Drain
Gate
FET
Gate
CGD
gm
ZL
Source
Source
Abbildung 4.6: Modell eines FETs zur Untersuchung der parasitären Feedbacks. Der
Gate-Anschluss koppelt über die Miller-Kapazität CGD an den DrainAnschluss. Zischen Drain und Source bzw. Erdung ist der FET als
Parallelschaltung der Steilheit gm und einer Last ZL modelliert. ZL
beinhaltet insbesondere den Drain-Source-Widerstand RDS des FETs
selbst.
Im allgemeinen Fall wird RDS durch eine beliebige komplexwertige Lastimpedanz
ZL ersetzt. Das Modell ist in Abbildung 4.6 dargestellt.. Interessant ist, zu welcher
Art Eingangsimpedanz ZL in einem FET führt, um zu verstehen, wie diese manipuliert werden kann. Das Verhalten des FETs wird durch folgende Gleichungen
48
4.3 Parasitäres Feedback
charakterisiert:
IS = IG + ID
IG =
1
1
ωCGD
(UG − UD )
(4.19)
(4.20)
UD = −ID ZL
(4.21)
IS = gm UG
(4.22)
Die ersten drei Gleichungen entsprechen den Kirchhoffschen Gesetzen, die dritte
Gleichung beschreibt die Verstärkung eines idealen FETs. Die effektive Eingangsimpedanz ergibt sich dann zu
Zin =
ZL + ωC1GD
UG
=
IG
1 + gm ZL
(4.23)
Dabei handelt es sich zunächst um eine Reihenschaltung, die Zin ergibt. Über eine
Impedanztranformation zu einer Parallelschaltung ergeben sich folgende Ergebnisse
[Ulm11]:
• Ohmsche Last am Ausgang des FETs ergibt zusätzliche Eingangskapazität Cin
sowie effektiven ohmschen Parallelwiderstand Rin . Eine Erhöhung der ohmschen Last bewirkt ein Absinken des Eingangswiderstands.
• Reine kapazitive Last ergibt ohmschen Parallelwiderstand am Eingang
• Induktive Last bewirkt negativen ohmschen Widerstand am Eingang. Dies bedeutet, dass positives Feedback auf den Eingang besteht, das anliegende Signal
erfährt eine Verstärkung.
Der letzte Punkt bewirkt eine Aufheizung des Teilchens. Interessant für das vorliegende Design ist besonders der erste Punkt, da am Ausgang des FETs der Arbeitswiderstand sowie eben der Drain-Source-Widerstand RDS des FETs selbst liegt. Insbesondere der so am Eingang entstehende Parallelwiderstand bewirkt eine Reduzierung
des gesamten Parallelwiderstands des Nachweiskreises, was zu verhindern ist. Somit
sollte parasitäres Feedback auf ein Minimum beschränkt werden, was insbesondere
eine Minimierung der Millerkapazität CGD fordert.
49
4 Der kryogene Verstärker
4.4 Design
In diesem Abschnitt wird das Design des Verstärkers beschrieben und die mechanische Fertigung ausgeführt.
Das Design folgt einem Vorschlag von Sven Sturm, der das Design zur Verwendung
an einem Experiment zur g-Faktormessung an 28 Si13+ entwickelte [Stu12]. Abbildung
4.7 zeigt den Aufbau.
Drain
Signalpout
R5
150
C5
1μ
3SK124
Gatep2
R9
680
R6
260
R3
560k
Sourcefolger
Rwork
1k
3SK124
Gatep1
NE25139
R1
560k
C1
1μ
R8
560k
R7
560k
C3
10n
C6
1μ
Gate
Sourcefolger
C4
1μ
NE25139
R2
100M
Kaskodenschaltung
C2
27p
Signalpin
Abbildung 4.7: Schaltschema das Verstärkers. Angaben für Widerstände in Ω, für
Kapazitäten in F. Genauere Beschreibung im Text.
Das Signal liegt über eine Koppelkapazität an den Gate-Anschlüssen zweier parallel geschalteter Dual-Gate-MESFETS des Typs NE25139 an. Sie wurden verwendet,
da gezeigt wurde, dass sie einen hohen Eingangswiderstand sowie eine geringe GateDrain-Kapazität besitzen [Ulm11]. Es folgt ein MESFET 3SK124 in Gate-Schaltung,
der gemeinsam mit den Eingangs-FETs eine Kaskodenschaltung bildet. Das Signal
liegt an einem Arbeitswiderstand Rwork = 1 kΩ an. Schlussendlich wird das Signal zu einem weiteren 3SK124 -FET in Drain-Schaltung geführt, der als Sourcefolger fungiert und das Signal mit einer geringeren Ausgangsimpedanz widergibt. Die
50
4.4 Design
Drain-Versorgung der Kaskode und des Sourcefolger erfolgt über einen Anschluss,
die Gate-Anschlüsse aller FETs sind separat über das jeweilige Biasing ansteuerbar.
Jeder Versorgungsanschluss ist mit einer 1 µF-Kapazität gegen Masse geschaltet, um
eventuelle Spannungsschwankungen der Spannungsversorgung herauszufiltern.
Die Auswahl der Bauteile und die technische Fertigung des Verstärkers folgten den
Untersuchungen von Stefan Ulmer [Ulm11]. Hier sind folgende Punkte zur Fertigung
eines Verstäkers mit den erforderlichen Eigenschaften gegeben:
• Wähle einen GaAs-FET mit einer geringen Gate-Drain-Kapazität
• Verwende Platinenmaterial mit geringer dielektrischer Permittivität und kleine
Abmessungen des gesamten Layouts. Als Platinenmaterial eignet sich Hochleistungsrf-Laminat etwa von Taconic.
• Verwende SMD-Bauteile (surface mounted devices) mit geringem intrinsischen
Verlustwinkel, um parasitäre Kopplungen zu verhindern
• Schaffe eine angemessenen Massenanschluss, um parasitäre Kopplungen von
Ausgang und Eingang zu vermeiden
• Verhindere Einflüsse des Signals auf die Impedanzen der Gleichstromversorgung der FETs. Dazu ist eine angemessene Erdung erforderlich.
Diesen Regeln entsprechend wurden die Dual-Gate-MESFETs ausgewählt. Nach
Messungen von Ulmer [Ulm11] zeigen sie eine Gate-Drain-Kapazität von 0,03 pF.
Die Kaskodenschaltung verringert die Miller-Kapazität. Als Platine wurde doppelt
beschichtetes Kupfer-TLC-Laminat der Firma Taconic verwendet. Die Fertigung erfolgt per Hand mit einer Fräsmaschine. Die Masseflächen wurden durchbohrt und
durch Einbringen von kurzen Kupferkabelstücken mit der Rückseite der Platine verbunden. Die Befestigung erfolgte durch Löten. Solche Durchführungen dienen dazu,
die Masse besser zu definieren. Parasitäre Kopplungen werden unterdrückt. In Untersuchungen zeigte sich, dass die Anzahl der Durchführungen einen großen Einfluss
auf den späteren effektiven Parallelwiderstand des gesamten Nachweisschwingkreises
hat, viele Durchführungen entsprechen dabei einem gewünschten höheren Widerstand [Ulm11]. Weiterhin wird die Rückkopplung des Signals auf den Resonator und
damit auf die Teilchenbewegung reduziert. Der vorliegende Verstärker wurde aus
einer Kupferplatine der Größe 20mm x 40mm hergestellt. Die Masseflächen wurden durch insgesamt 40 Durchführungen mit der Rückseite verbunden. Als Bauteile
wurden 0805-SMD-Komponenten gewählt. Dabei wurden Widerstände der Firma
51
4 Der kryogene Verstärker
Blackstar-Components und Kondensatoren von Johanson-Technology bzw. ECHU
für die µF-Kondensatoren ausgewählt. Die Bauteile zeigten sich in der bisherigen
Verwendung robust über mehrere Kühl- und Erwärmungsvorgänge und zeigten beim
Herabkühlen von Raumtemperatur in den kryogenen Bereich lediglich Abweichungen
von etwa 10% [Ulm11].
Die gesamte Platine wurde auf eine Kupferplatte aufgelötet, die zur thermischen
Ankopplung an den Kryostaten sowie zum elektrischen Anschluss der Massefläche
diente. Abbildung 4.8 zeigt den Verstärker.
Gate 1
KaskodenFET
Gate 2
Drain
2 cm
Eingang
Signal
EingangsFETs
4 cm
Sourcefolger
Ausgang
Signal
Abbildung 4.8: Beschriftete Fotografie des Verstärkers. Die Anschlüsse und Transistoren sind gekennzeichnet. Die beiden Eingangs-FETs wurden
übereinander installiert. Das beidseitig beschichtete Kupfer-TLCLaminat, auf dem sich die Bauteile befinden, wurde auf eine Kupferplatte aufgelötet.
Eine zentrale Motivation zum Aufbau dieses Verstärkerdesigns ist die Verwendung
von zwei Eingangs-FETs. Im bisherigen Experiment ist ein Verstärker mit einem
Eingangs-FET verbaut. Das Spannungsrauschen, das, wie in Abschnitt 3.3 beschrieben ein wichtiger limitierende Faktor des Signal-Rausch-Verhältnisses ist, kann auf
diese Weise verringert werden. Die Funktionsweise ist schematisch in Abbildung 4.9
dargestellt.
52
4.4 Design
R
R
R
en
in
R
R0
in
in,0
R0
en,0
en
Abbildung 4.9: Schematische Darstellung zur Parallelschaltung zweier stochastisch
unabhängiger Rauschquellen. Dadurch
√ lässt sich eine Verringerung
der Rauschleistung um den Faktor 2 erreichen.
Die beiden Eingangs-FETs sind zu diesem Zweck durch eine Parallelschaltung
zweier rauschender Widerstände dargestellt. Diese werden in einen rauschfreien Widerstand R und in Reihe dazu einer Spannungsrauschquelle en unterteilt. Zunächst
lässt sich diese Spannungsrauschquelle dann in eine parallele Stromrauschquelle in
umschreiben:
in =
en
R
(4.24)
Es ergibt sich eine Parallelschaltung beider Widerstände und beider Stromrauschquellen. Diese können jeweils zusammengefasst werden, die Widerständer zu
R0 = 2 · R−1
−1
R
2
=
(4.25)
und die Stromrauschquellen addieren sich als voneinander stochastisch unabhängige Signale quadratisch zu
in,0 =
p
2 · i2n
(4.26)
Schlussendlich lassen sich so beide Rauschwiderstände zu einem einzigen Widerstand R0 zusammenfassen, dessen Rauschleistung beträgt dann
en,0 = R0 in,0
p
R
= R0 2 · i2n =
2
r
2·
e 2
n
R
en
=√
2
(4.27)
Damit bewirkt dieses Design eine voraussichtliche Erniedrigung der Spannungsrauschleistung um den Faktor
√1
2
im Vergleich zur Auslegung mit nur einem Eingangs-
FET. Allerdings ergeben sich dadurch andere, nachteilhafte Auswirkungen auf den
53
4 Der kryogene Verstärker
Gesamtnachweis. So ist bei zwei FETs die kapazitive Kopplung des Eingangs an das
verstärkte Ausgangssignal höher, was zu einer höheren Eingangskapazität und einem
geringeren Eingangswiderstand führen kann (vgl. Kapitel 4.3).
54
4.5 Experimentelle Ergebnisse
4.5 Experimentelle Ergebnisse
4.5.1 Der Pulsrohr-Kühler
Für die Messaufbauten und Resultatermittlungen im kryogenen Bereich wird der hier
beschriebene Messstand verwendet, dessen Herzstück ein Pulsrohr-Kühler bildet.
In seiner grundsätzlichen Form entwickelt und beschrieben wurde dieser Teststand
ausführlich in der Diplom-Arbeit von Stefan Ulmer [Ulm06]. Er besteht aus einem
19’-Rack, an der der Pulsrohrkühler aufgehängt ist. Dieser ist ein zweistufiger Gasexpansionskühler von Grifford-McMahon (Abbildung 4.10). An der ersten Stufe wird
bei einer Kühlleistung von 7W eine Temperatur von etwa 77K, an der zweiten Stufe
4K bei 350 mW Leistung erzielt.
Abbildung 4.10: Abbildung des verwendeten Pulsrohrkühlers des Herstellers
VERICOLD
Die für die kryogenen Tests benötigte untere Stufe ist im Teststand komfortabel
zugänglich. Hier lassen sich die verschiedenen Bauteile montieren und mit KryoKoaxialkabeln anschließen, die aus dem Kühler herausgeführt werden. An die Unterseite des Kühlers kann über einen CF-200-Flansch eine Vakuumkammer ange-
55
4 Der kryogene Verstärker
bracht werden. Teil dieser ist ein Messstutzen, der einige seitlich angebrachte CF-40Flansche besitzt, über die die elektronischen Zuleitungen sowie Sensoren für Temperatur und Druck und das Vakuumpumpensystem angebracht werden können. Abgeschlossen wird die Kammer durch ein stabiles, abgeschlossenes Rohr. An die erste
Stufe des Kühlers kann innerhalb der Vakuumkammer ein Hitzeschild installiert werden, um die Wärmelast auf Stufe 2 zu verringern. Dabei handelt es sich um einen
mit Super-Isolator ummantelten geschlossenen Edelstahl-Zylinder.
Im Teststand lassen sich geringe Abkühl- und Aufwärmzeiten realisieren, womit
eine zügige Durchführung verschiedener Messungen möglich ist. Die untere Stufe
erreicht bereits nach wenigen Stunden eine Temperatur, die nur geringfügig über
der schließlich erreichten Endtemperatur liegt. Diese wurde zu 3K bestimmt. Hierbei
spielt neben der Masse des montierten Objekts auch die thermische Ankopplung eine
wichtige Rolle. Ein Vakuum hoher Güte ist Grundvoraussetzung. Die Aufwärmzeit
hängt vom Wärmeeintrag auf die Kühlstufen ab. Auch hier spielt die Güte des Vakuums, Größe und Masse des Testobjekts wichtige Rollen. Als Richtwert können etwa
12 Stunden angenommen werden.
Während des Testens und Modifizierens des Verstärkers wurde im Allgemeinen
folgende Routine durchgeführt: Das Testobjekt wurde mechanisch ruckelfrei an die
untere Stufe angeschraubt. Zur besseren Wärmeleitung wurde nach Bedarf Leitpaste
aufgetragen. Nach ebenfalls ruckelfreier Befestigung von Hitzeschild und Vakuumkammer wurde ein Vorvakuum im Bereich 10−2 bis 10−3 mbar gepumpt. Danach
wurde über eine Turbomolekularpumpe ein Druck von etwa 10−5 mbar erreicht.
Diese Prozedur nimmt etwa eine Stunde in Anspruch. Danach wurde der Kühler
eingeschaltet und am nächsten Tag die Messungen durchgeführt. Durch Einfrieren
des Restgases an den Wänden der Vakuumkammer befand sich der Druck dann im
Bereich von 10−8 mbar. Nach Durchführung der Messung wurde die Kühlung abgeschaltet und die Apparatur erwärmte sich bis zum folgenden Tag. Nach Brechen des
Vakuums können dann erneut Modifikationen am Versuchsaufbau an der kalten Stufe
durchgeführt werden. Ein Messzyklus aus Aufbauen, Kühlen und Messen benötigte
somit zwei Tage.
Die Temperaturaufnahme erfolgt über einen CERNOX CU CX-1050 -Temperatursensor
der Firma Lakeshore.
4.5.2 Verstärkung
Die Verstärkung wurde mit dem Netwerkanalysator HP 3577 A von Hewlett &
Packard bestimmt. Das Signal wurde für die Tests in kryogener Umgebung vom
56
4.5 Experimentelle Ergebnisse
Ausgang des Analysators über ein Koaxialkabel an die Anschlüsse am Flansch des
Teststandes geführt. Als Signalfrequenz wurden 750 kHz gewählt, was sich im Bereich der axialen Frequenz des Teilchens in der Penningfalle von etwa 700 kHz. befindet. Die Bandbreite betrug 10 kHz, ein Sweep des Signals über diese Bandbreite
betrug 1s. Zur Ermittlung der Verstärkung wurde die geringstmögliche einstellbare
Signalleistung von -49 dBm gewählt. Der Ausgang des Verstärkers wurde nach Herausführen aus dem Teststand ebenfalls per Koaxialkabel an den Eingang des Analysators geschaltet. Dabei wurde die 50-Ω-Einstellung verwendet, da auch im Betrieb
des Verstärkers später ein Raumtemperatur-Nachverstärker mit dieser Eingangsimpedanz verwendet wird. Aus der Differenz der Signalstärken wird die Verstärkung in
dB bestimmt.
1 5
1 0
Verstärkung (dB)
5
0
-5
-1 0
Spannung an Gate 2 (V)
-1 5
0
-0,7
-1,0
-1,3
-2 0
-2 5
-3 0
-0 ,8
-0 ,7
-0,5
-0,9
-1,2
-0 ,6
-0 ,5
Spannung an Gate 1 (V)
-0 ,4
Abbildung 4.11: Verstärkung bei verschiedenen Arbeitspunkten. Gate 1 ist der Anschluss der Eingangs-FETs, Gate 2 der Anschluss des KaskodenFETs.
Interessant ist die Veränderung der Verstärkung bei Variation der Spannungen an
den Gate-Anschlüssen der Eingangs-FETs sowie am Gate des Kaskoden-FETs. Die
Spannung am Gate des Sourcefolgers wurde so eingestellt, dass bei Konstanthalten
der übrigen Parameter die maximale Verstärkung erreicht wurde. Der Sourcefolger ist
57
4 Der kryogene Verstärker
nur für die Wandlung der Ausgangsimpedanz nötig und muss zur Untersuchung der
weiteren Eigenschaften des Verstärkers nicht weiter untersucht werden. Die gefundene
Spannung ergab sich zu -0,7 V und wurde bei den weiteren Tests nicht verändert. Die
Spannung an der gemeinsamen Drain-Versorgung wurde vorausschauend so gewählt,
dass bei Variation der Gate-Spannungen eine Leistungsabgabe von 10 mW nicht
überschritten wird (vgl. Abschnitt 4.5.3). Die hier gewählten 2 V wurden in den
weiteren Messungen ebenfalls nicht variiert. Qualitativ anzumerken ist hier, dass die
Verstärkung bei Erhöhung der Drainspannung ansteigt.
Abbildung 4.11 zeigt die erhaltenen Verstärkungen bei Variation der Gate-Spannungen.
Im Folgenden wird der Anschluss für die Gate-Anschlüsse der beiden Eingangs-FETs
als „Gate 1“ bezeichnet, der Anschluss für das Gate des Kaskoden-FETs als „Gate
2“. Hieraus kann abgelesen werden, in welchen Bereichen bzw. Arbeitspunkten ein
Betrieb des Verstärkers sinnvoll ist. Aus der Abbildung ist das charakteristische
Verhalten von Transistoren deutlich ersichtlich: Für Arbeitsbereiche außerhalb der
Region mit hoher Steilheit gm liegt keine Verstärkung vor. Die Gate-Spannung muss
also so gewählt werden, dass hohes gm erreicht wird. Es ist ersichtlich, dass für Gate
1 Betriebsspannungen im Bereich zwischen -0,65 und -0,55 V gewählt werden sollten.
Die Einstellung an Gate 2 spielt im Bereich bis etwa - 1V eine untergeordnete Rolle,
höhere negative Spannungen bewirken ein deutliches Absinken der Verstärkung. Der
maximal erreichbare Wert ergab sich für eine Spannung von -0,6 V an Gate 1 und
-0,7 V an Gate 2 und betrug 13,6 dB. Das entspricht einem Verstärkungsfaktor der
Spannungsamplitude von 4,8. Der oben genannte Bereich der Arbeitspunkte liefert
mit 8 dB schlechtestenfalls einen Verstärkungsfaktor von 2,5.
4.5.3 Leistungsaufnahme
Die Leistungsaufnahme des Verstärkers ist wichtig, da sie sich durch Wärmedissipation äußert. Um den kryogenen Betrieb aufrecht zu erhalten, darf sich der Verstärker
lokal nicht zu stark erhitzen. Des Weiteren könnte dies zu einer Aufheizung der
supraleitenden Resonatoren über die Sprungtemperatur führen. Mit einer Leistungsaufnahme von unter 10 mW ist dies gewährleistet [Kra07] [Ulm11]. Abbildung 4.12
zeigt die Leistungsaufnahme in Abhängigkeit einiger ausgewählter Arbeitspunkte bei
Betrieb in kryogener Umgebung.
Die Leistungsaufnahme wurde aus dem Produkt der Spannung an der Drainversorgung und dem mit einem FLUKE 189 True RMS -Tischmultimeter aufgenommenen
Strom an diesem Anschluss errechnet. Die Spannung betrug stets 2 V und wurde
nicht variiert. An den Gate-Anschlüssen der FETs ist nicht mit einem nennenswer-
58
4.5 Experimentelle Ergebnisse
6 ,5
S p a n n u n g a n G a te 2 (V )
L e is tu n g s a u fn a h m e ( m W )
6 ,0
0
-0 ,5
-0 ,9
-1 ,2
-0 ,7
-1 ,0
-1 ,3
5 ,5
5 ,0
4 ,5
4 ,0
-0 ,8
-0 ,7
-0 ,6
-0 ,5
-0 ,4
S p a n n u n g a n G a te 1 (V )
Abbildung 4.12: Leistungsaufnahme des Verstärkers bei verschiedenen Arbeitspunkten. Gate 1 ist der Anschluss der Eingangs-FETs, Gate 2 der Anschluss des Kaskoden-FETs. Die Leistung wurde über den am Drainanschluss fließenden Strom ermittelt.
ten Stromfluss zu rechnen, was mit einem Messgerät auch bestätigt werden konnte.
Der Verlauf der Graphen kann durch den inneren Aufbau des Verstärkers verstanden werden. Die verwendeten MESFETs sind normal-leitend, d.h. bei einer GateSpannung von 0 V ist der Drain-Source-Widerstand klein. Mit ansteigender GateSpannung steigt auch er. Das erklärt den Abfall des Drainstroms und damit auch
der Leistungsaufnahme von niedrigen negativen zu hohen negativen Spannungen an
beiden Gate-Anschlüssen. Für große Spannungen an Gate 1 dominiert dessen Widerstand die gesamte Drain-Source-Strecke, mit Variation von Gate 2 ist kein Unterschied zu erkennen. Ein Teil des Stroms fließt über den Sourcefolger, dessen Einstellungen im Test nicht verändert wurden. Die erreichten Werte sind mit unter 6,5
mW ausreichend gering.
59
4 Der kryogene Verstärker
4.5.4 Spannungsrauschen
Für die Messungen des Rauschens wurde der Spektrum-Analysator Rohde & Schwarz
FSP-13 verwendet. Die Funktionsweise und empfohlenen Einstellungen sind dem
Handbuch [Sch06] sowie [Agi06] zu entnehmen. Der Spektrum-Analysator (im Folgenden „FSP“ genannt) gibt die ermittelten Daten auf einem Digital-Display mit 501
Bildpunkten aus. Damit repräsentiert ein Bildpunkt 1/500 der gesamten eingestellten
Frequenzbandbreite („Span“), die untersucht wird. Zur Messung der Rauschleistungsdichte stellt der FSP zwei Detektorausführungen zur Verfügung. Der RMS -Detektor
errechnet den quadratischen Mittelwert der Messwerte eines Bildpunktes, während
der Sample-Detektor die Abtastwerte ohne weitere Bewertung präsentiert. Die pro
Bildpunkt verwendete Abtast- bzw. Mittelungszeit hängt von der Wahl der Auflösebandbreite (resolution bandwidth = RBW) und der gesamten für einen Durchlauf (Sweep) zu Verfügung gestellten Zeit ab. Der FSP zerlegt die zu untersuchende
Bandbreite in Einheiten der RBW, die einzeln ausgewertet werden. Beim SampleDetektor müssen im Vergleich zum RMS -Detektor zwei Korrekturen beachtet werden. So müssen 1,05 dB addiert werden, um den Unterschied zwischen Mittelwert
und Effektivwert bei weißem Rauschen abzubilden. Innerhalb der RBW kann von
einer frequenzunabhängigen Rauschamplitude ausgegangen werden. Außerdem müssen weitere 1,45 dB einberechnet werden, fall die logarithmische Darstellung gewählt
wurde, in der Spitzenwerte der Rauschamplituden unterwertet werden. Der Detektor Sample führt diese Korrekturen intern durch und zeigt die korrigierten Werte
am Display an. Es wurde die Ausgabeoption in linearen Einheiten gewählt, der FSP
gibt dann die Rauschamplitude in
√nV
Hz
in Bezug auf 1Hz Bandbreite aus. Der Sam-
ple-Detektor wurde gewählt, da hier eine Mittelung der Ergebnisse durch mehrere
Sweeps über die gesamte untersuchte Bandbreite möglich ist. So lässt sich am Display direkt eine Stabilisierung der Messwerte mitverfolgen.
Um das Spannungsrauschen des Verstärkers zu ermittlen, wird das Rauschsignal des kryogenen Verstärkers nochmals mit Hilfe eines Raumtemperaturverstärkers
ZFL-500-LN der Firma Mini Circuits nachverstärkt. Dies ist nötig, damit das Signal
deutlich über dem Eingangsrauschen des FSP liegt.
Der komplette Aufbau zum Messen des Rauschens ist in Abbildung 4.13 dargestellt. Der Eingang des Verstärkers wird mit einem Widerstand im Raumtemperaturbereich abgeschlossen. Der Ausgang wird an den ZFL angeschlossen, das Signal
danach zum Detektor geführt.
Damit liegt am Eingang des Verstärkers neben dessen zu bestimmendem Span-
60
4.5 Experimentelle Ergebnisse
Kryogener
Verstärker
ZFL
eth
GAmp
R
eFSP
eZFL
en
FSP
Detektor
GZFL
in
Abbildung 4.13: Schematische Darstellung des Messaufbaus zur Ermittlung des Eingangsrauschens des Verstärkers. Der Eingang wird mit einem Widerstand abgeschlossen. Zum Gesamtrauschen eges , das am FSP detektiert wird, tragen auch das Rauschen des Nachverstärkers (ZFL)
und das Eingangsrauschen des FSPs bei.
nungsrauschen en und Stromrauschen in auch das thermische Rauschen eth des Widerstands. Dies alles wird über den Verstärker mit linearer Verstärkung GAmp zum
ZFL geführt. Dieser ist durch sein Eingangsrauschen eZF L und seine Verstärkung
GZF L modelliert. Schließlich addiert sich zum Signal noch das Eingangsrauschen
e2F SP des FSPs. Am Detektor ist das Gesamtrauschen eges zu sehen. Mit quadratischer Addition der Rauschbeiträge als unkorrelierte Quellen gilt
e2ges =
4kB T R + e2n + i2n R2 · G2Amp + e2ZF L · G2ZF L + e2F SP
(4.28)
Für die Messungen wurde am Detektor Sample ein Frequenzband von 748 bis
752 kHz eingestellt. Die Auflösebandbreite betrug 300 Hz, die Videobandbreite 30
Hz. Ein Sweep benötigte 1s, es wurde über etwa 100 Sweeps gemittelt, bis am Display
keine Veränderung des gemessenen Rauschens mehr beobachtet werden konnte.
Das Rauschen des FSP eF SP kann direkt durch Abschluss des Eingangs mit einem
kleinen Widerstand (50Ω) gemessen werden. Es ergab sich zu
nV
eF SP = 16.3 √
Hz
(4.29)
Aus einer Schaltung analog zu Abbildung 4.13 unter Auslassen des Verstärkers
61
4 Der kryogene Verstärker
selbst kann auf das Rauschen des ZFL geschlossen werden
nV
eZF L = 0.6 √
Hz
(4.30)
Das Rauschmaß N F ist im Datenblatt mit 2,9 dB angegeben.
Aus einer separaten Verstärkungsmessung erhält man auch die Verstärkung
GZF L = 30 dB =
b 31, 6
(4.31)
Zur Bestimmung des Spannungsrauschens wird ein kleiner Eingangswiderstand R
benötigt. Im Experiment wurde ein Kurzschluss verwendet, wodurch das thermische
Spannungsrauschen des Widerstands und das Stromrauschen entfällt. Gleichung 4.28
vereinfacht sich zu
e2ges = e2n · G2Amp + e2ZF L · G2ZF L + e2F SP
(4.32)
Daraus ergibt sich das gesuchte Spannungsrauschen en zu
en =
1
GAmp
s
e2ges − e2F SP
− e2ZF L
G2ZF L
(4.33)
Die Werte für GAmp bei verschiedenen Arbeitspunkten können aus den vorherigen
Messungen aus Abschnitt 4.5.2 übernommen werden. Abbildung 4.14 zeigt das Spannungsrauschen für verschiedene Einstellungen der Spannungen an den Anschlüssen
Gate 1 und Gate 2.
Es ist deutlich zu sehen, dass das Spannungsrauschen für die Einstellungen minimal
ist, die auch schon für die höchstmögliche Verstärkung gewählt werden mussten. Im
Bereich der Spannung an Gate 1 von den in Abschnitt 4.5.2 herausgegriffenen -0,55
bis -0,65 V und im Bereich von 0 bis -1 V bei Gate 2 liegt das Rauschen zwischen 0,25
und 0,4 √nV
und damit deutlich unter dem Wert von 1,6 √nV
im bisher verbauten
Hz
Hz
Verstärker. Im Arbeitspunkt mit der größten Verstärkung (Gate 1 = -0,6 V, Gate 2
bestimmt.
= -0,7 V) wurde ein Spannungsrauschen von 0,32 √nV
Hz
Interessant ist in diesem Zusammenhang auch die Frequenzabhängigkeit des betrachteten Spannungsrauschens. Dazu wurde im Bereich von 0 bis 3 MHz in einer
Auflösebandbreite von 6 kHz ein detailliertes Rauschspektrum aufgenommen, wobei die Gate-Spannungen mit der oben beschriebenen höchsten Verstärkung gewählt
wurden. Die Berechnung des Eingangsrauschens von FSP und ZFL erfolgte analog
wie oben beschrieben. Die Verstärkung fiel zu steigenden Frequenzen hin leicht ab,
62
4.5 Experimentelle Ergebnisse
2 ,0
S p a n n u n g a n G a te 2 (V )
1 ,6
S p a n n u n g s ra u s c h e n (n V /H z
0 ,5
)
1 ,8
1 ,4
0
1 ,2
-0 ,7
-1 ,0
-0 ,5
-0 ,9
1 ,0
0 ,8
0 ,6
0 ,4
0 ,2
0 ,0
-0 ,8
-0 ,7
-0 ,6
-0 ,5
-0 ,4
S p a n n u n g a n G a te 1 (V )
Abbildung 4.14: Spannungsrauschen des Verstärkers für verschiedene Arbeitspunkte.
Das Rauschen erreicht ein Minimum bei den Arbeitspunkten mit
den günstigsten Parametern für die Verstärkung.
was in der Berechnung berücksichtigt ist. Abbildung 4.15 zeigt das Ergebnis.
Die oben bestimmten 0,3 √nV
für eine Frequenz von 750 kHz finden sich wieder.
Hz
Weiterhin ist das Abfallen des Rauschens zu höheren Frequenzen hin deutlich ersichtlich. Wie bereits in Abschnitt 4.2 beschrieben, setzt sich das Spannungsrauschen aus
einem frequenzabhängigen „rosa“ Anteil und einem festen „weißen“ Anteil zusammen.
Als einfaches Modell wurde daher die Gleichung
en (ν) = a ·
1
+b
ν
(4.34)
mit Konstanten a und b angepasst. Das Modell beschreibt den Verlauf der Messwerte treffend, die ν1 -Charakteristik ist gut zu erkennen. Über eine grafische Ermittlung
lässt sich auch die Rauschkante bestimmen [Tex01]: Das Rauschen scheint ab einer
Frequenz von etwa 2 MHz nicht weiter abzusinken, sondern auf einem Niveau von
etwa 0,2 √nV
zu verharren.
Hz
63
4 Der kryogene Verstärker
1 ,4
R a u s c h e n in n V /H z
0 ,5
1 ,2
1 ,0
0 ,8
0 ,6
0 ,4
0 ,2
0 ,0
0 ,5
1 ,0
1 ,5
2 ,0
2 ,5
3 ,0
F r e q u e n z in M H z
Abbildung 4.15: Spannungsrauschen des Verstärkers in Abhängigkeit der Frequenz.
Eine Anpassung eines Modells zeigt ein Verhalten gemäß a · ν1 + b
mit Konstanten a und b.
Um das Stromrauschen am Eingang des Verstärkers zu untersuchen, ist nach
Gleichung 4.28 ein großer Eingangswiderstand nötig. Ein solcher kann durch einen
Resonator hoher Güte realisiert werden, wie er auch im Nachweiskreis des Experiments zum Einsatz kommt. Der für den Teststand verwendete Resonator wird im
folgenden Abschnitt charakterisiert, bevor die dadurch ermöglichten Messungen vorgestellt werden. Das Stromrauschen ist in Abschnitt 4.5.8 dargestellt.
4.5.5 Der Resonator im Teststand
Für die Messung der Eingangskapazität und des Eingangswiderstands sowie zur Ermittlung des Stromrauschens wird ein Resonator im Teststand installiert, der an
den Eingang des Verstärkers angeschlossen wird. Dieser sollte eine hohe Güte und
damit einen hohen Parallelwiderstand Rp besitzen. Der als Parallelschwingkreis in
Abschnitt 3 eingeführte Resonator besteht im Experiment aus einer aus NbTi auf
einen PTFE-Kern gewickelten Spule. Sie ist in einem zylindrischen, ebenfalls su-
64
4.5 Experimentelle Ergebnisse
praleitenden Gehäuse montiert. Abbildung 4.16 zeigt das am Teststand installierte
Gehäuse. Zur besseren Kühlung wurde noch ein Schlauch aus Kupfergeflecht darum gelegt und mit Kupferlitzen straff gespannt. Eine solche komplette Umwicklung
ist nötig, da ein Supraleiter im supraleitenden Zustand seine Wärmeleitfähigkeit verliert. Die thermische Ankopplung an die zweite Stufe des Kühlers erfolgte durch festes
Anschrauben der Litzen. Am unteren Ende des Kupferschlauches wurde ein zweites
Thermometer installiert, um ein eventuelles Temperaturgefälle zwischen kalter Stufe
und Bodes des Resonatorgehäuses feststellen zu können.
Abbildung 4.16: Gehäuse des Resantors an der kalten Stufe des Pulse Tubes befestigt. Zur besseren thermischen Ankopplung wurde später noch ein
Kupfergeflecht darum gelegt.
Der Resonator ist durch seine Kapazität, Induktivität und den Parallelwiderstand
bestimmt. Zu deren Ermittlung wurde wie zur Verstärkungsmessung des Verstärkers
der Netzwerkanalysator HP 3577A verwendet. Das Ausgangssignal wurde über BNCKabel in das Vakuum geführt. Die Ankopplung an den Resonator erfolgte kapazitiv,
indem das signalführende Kabel mechanisch mittels Teflonband auf dem zur Spule
führenden Kabel befestigt wurde (siehe Abbildung 4.17.
Diese Ankopplung sollte so gering wie möglich sein, um dämpfende Einflüsse durch
65
4 Der kryogene Verstärker
Einkopplung
Einkopplung
Auskopplung
Auskopplung
Abbildung 4.17: Schematische Darstellung der Ankopplung des Testresonators. Das
vom Netzwerkanalysator kommende Signal wird kapazitiv in den
Resonator eingespeist. Um dessen Kapazität und Induktivität zu
bestimmen, wird in einer zweiten Messung eine bekannte Kapazität
parallel geschaltet.
die Kabel oder den Netzwerkanalysator selbst zu minimieren. Am Analysator wurde danach die Resonanzkurve der Transferfunktion untersucht. Wie in Abschnitt 3
bereits dargelegt, kann aus der 3dB-Breite ∆ν und der Mittenfrequenz ν0 die Güte
bestimmt werden:
Q=
ν0
∆ν
(4.35)
Abbildung 4.18 zeigt eine im Experiment erhaltene solche Transferfunktion mit
den benötigten Größen, die direkt am Analysator abgelesen werden können. Für das
konkrete Beispiel ergibt sich eine Güte von Q = 2000.
Der Einfluss der Signalstärke auf die Transferfunktion wurde überprüft, indem sie
schrittweise erhöht und die 3dB-Breite bestimmt wurde. Bei einer Ausgangssignalstärke von unter 30dBm konnte bei Verringerung keine weitere Verschmälerung des
Peaks erreicht werden, so dass hier davon ausgegangen werden kann, dass die Güte
nicht durch die Signalstärke limitiert wird. Weiterhin wurde sichergestellt, dass die
wählbare Eingangsimpedanz des Analysators ebenfalls keinen Einfluss auf das Resonatorverhalten hat. Dazu wurden am Eingang des Netzwerkanalysators die Eingangswiderstände 50 Ω und 1 kΩ gewählt, ohne dass ein Einfluss auf die Transferfunktion
sichtbar war. Die Messungen wurden mit der Einstellung 50 Ω durchgeführt.
Die Bestimmung von Kapazität und Induktivität des Resonators kann nicht in
einer einzigen Messung erfolgen. Wie in Abbildung 4.17 dargestellt, wurde eine Mes-
66
4.5 Experimentelle Ergebnisse
-5 5
-5 7
-6 0
3 dB
Signalstärke (dBm)
Signalstärke (dBm)
-5 8
-6 5
-5 9
-7 0
-6 0
-7 5
∆ν
-6 1
-8 0
-6 2
ν0
-8 5
-6 3
1 ,2 4
1 ,2 6
1 ,2 8
1 ,3 0
1 ,3 2
1 ,3 4
Frequenz (MHz)
1 ,3 6
1 ,2 9 0
1 ,2 9 2
1 ,2 9 4
1 ,2 9 6
1 ,2 9 8
Frequenz (MHz)
1 ,3 0 0
1 ,3 0 2
Abbildung 4.18: Transferfunktion des Testresonators. Links eine gröbere Darstellung, rechts eine detaillierte mit den zu messenden Werten. In diesem Fall ergibt sich eine Güte von Q = 2000.
sung mit dem unveränderten Resonator und eine mit einer parallel geschalteten
bekannten Kapazität durchgeführt. Für die Resonanzfrequenz des unmodifizierten
Resonators gilt
νLC =
1
√
= ν1
2π LCR
(4.36)
mit der Kapazität CR . Die parallele Kapazität Cp , im Experiment ein SMD-Bauteil
der Firma Johansson Technologies, verschiebt diese Resonanzfrequenz zu
νneu =
1
p
= ν2
2π L (CR + Cp )
(4.37)
Die Frequenzen werden gemessen, woraus sich schlussendlich die gesuchte Induktivität und Kapazität ermitteln lässt:
L=
1
2πν2
2
−
1
2πν1
2 !
·
1
Cp
(4.38)
sowie
Cp
C R = 2
ν1
ν2
(4.39)
−1
Bei der Messung des freien Resonators ergab sich ν1 = 2,143 MHz und nach Parallelschalten eines 5,1pF-Kondensators ν2 = 1,421 MHz. Damit hat der freie Resonator
die Kennwerte
67
4 Der kryogene Verstärker
L = 1.38mH
(4.40)
CR = 4.00pF
(4.41)
Rp = 550M Ω
(4.42)
Letzteres ist der effektive Parallelwiderstand des Resonators und ergibt sich aus
der 3dB-Breite von ∆ν = 72 Hz und damit der Güte Q = 29600 aus der in Abschnitt
3.1.1 abgeleiteten Beziehung
Rp = 2πν0 LQ
(4.43)
4.5.6 Eingangskapazität
Nachdem der Resonator im Teststand charakterisiert ist, kann er verwendet werden,
um weitere wichtige Eigenschaften des Verstärkers zu ermitteln. Die Eingangskapazität des Verstärkers beschreibt die kapazitive Ankopplung des Eingangs an den
Massenanschluss. Sie wirkt sich auf die Gesamtkapazität des Nachweiskreises aus
und hat Einflüsse auf die Ankopplung des Verstärkers an den Resonator. In Abbildung 4.19 ist der Messaufbau zur Bestimmung der Eingangskapazität Cin und des
Eingangswiderstands Rin dargestellt.
Der Verstärker wird über die Koppelkapazität CC = 27 pF an den im Abschnitt
4.5.5 beschriebenen Resonator im Teststand angeschlossen. In den Resonator wird
ebenso wie dort beschrieben ein Signal des Netzwerkanalysators eingespeist. Das
Ausgangssignal wird am Ausgang des Verstärkers abgenommen und wiederum auf
dem Analysator dargestellt. Mit den gleichen Methoden wie bei der Bestimmung der
Kapazität des Resonators selbst kann zunächst die gesamte durch den Verstärker
parallel hinzugefügte Gesamtkapazität Cges ermittelt werden:
Cges = CR
2
νf rei
νmess
− CR
(4.44)
−1
CR = 4,00 pF und νf rei = 2,143 MHz sind die in Abschnitt 4.5.5 ermittelten Werte des freien Resoantors, νmess die am Netzwerkanalysator ausgelesene neue Resonanzfrequenz nach Anschluss des Verstärkers. Die hieraus für die verschiedenen
Arbeitspunkte ermittelten Werte für Cges sind noch nicht die wie in Abbildung 4.19
68
4.5 Experimentelle Ergebnisse
Testresonator
Kompletter Verstärker
idealer
Verstärker
en
CC
Rp
Cp
Lp
in
Cin
Rin
Abbildung 4.19: Schematische Darstellung zur Messung von Eingangskapazität und
-Widerstand des Verstärkers. Über die auf der Verstärkerplatine
aufgelötete Koppelkapazität mit CC =27pF wird der Eingang des
Verstärkers angeschlossen. Als Charakteristik werden die zu Masse
anliegende Kapazität Cin und der Widerstand Rin bestimmt.
ersichtlich benötigten Werte für Cin , sondern geben den Wert der Reihenschaltung
von Cin mit der Koppelkapazität CC = 27 pF an. Somit gilt
Cin =
1
1
−
Cges CC
−1
(4.45)
Abbildung 4.20 gibt die ermittelte Eingangskapazität Cin für die bereits in den
anderen Messungen verwendeten Arbeitspunkte an.
Die erhaltenen Eingangskapazitäten bewegen sich im Bereich zwischen 8 und knapp
13 pF und sind stark von der Wahl der Spannungen an den Anschlüssen an Gate
1 und Gate 2 abhängig. Sie liegen damit höher als erwartet. Eine niedrige negative
Spannung an Gate 2, dem oberen FET der Kaskodenschaltung, bewirkt einen starken Anstieg der Kapazität im Bereich der größten Verstärkung (-0,55 bis -0,65V an
Gate 1). Während für Gate 2-Spannungen ab ca. -0,9 V bei Variation der Gate 1Spannung nur eine Änderung der Eingangskapazität um etwa 15% stattfindet, liegt
der bei einer Spannung von 0 V an Gate 2 ermittelte höchste Wert mit knapp 13pF
um fast 50% darüber. Der Grund hierfür ist die Steuerung der Kaskodenschaltung,
die vom Arbeitspunkt an Gate 2 abhängt. Ein Arbeitspunkt bei niedrigen Spannungen führt nicht zu dem gewünschten Effekt der Verminderung des Miller-Effekts
(vgl. Abschnitt 4.3). Da in diesem Verstärker zwei FETs parallel installiert sind,
ist ohnehin eine im Vergleich zu einem Eingangs-FET höhere Eingangskapazität zu
69
4 Der kryogene Verstärker
1 3
Eingangskapazität (pF)
1 2
1 1
1 0
9
Spannung an Gate 2 (V)
0
-0,7
-1,0
8
-0,5
-0,9
-1,2
7
-0 ,7
-0 ,6
-0 ,5
Spannung an Gate 1 (V)
-0 ,4
Abbildung 4.20: Eingangskapazität in kryogener Umgebung bei verschiedenen Arbeitspunkten des Verstärkers.
erwarten. Ein weiterer Grund für die hohe Eingangskapazität kann eine parasitäre
Kopplung des Eingangs an Masse sein, die durch unsaubere Verarbeitung der Platine oder Verunreinigungen entsteht. Bei späteren Messungen, in denen das Verhalten
des Verstärkers bei Entfernung eines Eingangs-FETs untersuch wird, wird dies noch
genauer betrachtet.
Der Anteil der Eingangskapazität, der tatsächlich auf den Resonator wirkt, ist von
der Ankopplung des Verstärkers abhängig. Koppelkondensator und Eingangskapazität bilden eine Reihenschaltung von Kapazitäten. Außerdem ist die Eingangskapazität grundlegend zur Ermittlung des Kopplungsfaktors α =
CC
CC +Cin ,
wie er in
Abschnitt 3 definiert ist und zur Ermittlung des Signal-Rausch-Verhältnisses benötigt wird. Somit spielt sie auch bei der Auswirkung des Eingangswiderstands des
Verstärkers auf den Parallelwiderstand des gesamten Nachweiskreises eine entscheidende Rolle.
70
4.5 Experimentelle Ergebnisse
4.5.7 Eingangswiderstand
Der Eingangswiderstand des Verstärkers spielt bei der Limitierung der Güte des
Nachweisschwingkreises eine entscheidende Rolle. Ein geringer Eingangswiderstand,
der parallel zum Resonanzwiderstand geschaltet wird, erniedrigt diesen. Somit ist ein
hoher Eingangswiderstand wünschenswert. Zwar kann durch Wahl der Ankopplung
des Verstärkers an den Resonator der Einfluss des Eingangswiderstands vermindert
werden gemäß
Rsys =
Cc + Cin
Cc
2
Rp +
Rp Rin
2
Cc +Cin
Cc
(4.46)
Rin
jedoch ermöglicht ein hoher Eingangswiderstand eine größere Variation der Ankopplung, was technisch leichter durchführbar ist. So ist am Experiment derzeit eine
induktive Abkopplung durch einen Tap an der Spule von 0,2 realisiert.
Die Messung erfolgt nach dem gleichen Aufbau wie zur Bestimmung der Eingangskapazität nach Abbildung 4.19. Das Hinzufügen des Eingangswiderstands bewirkt ein
Absinken des gesamten effektiven Parallelwiderstands Rp des Systems, was eine Verbreiterung der 3dB-Breite und eine Herabsenkung der Güte bedeutet.Diese wurde
für verschiedene Arbeitspunkte aufgenommen und daraus mit der bekannten Induktivität des Resonators L = 1,38mH gemäß Rmess = 2πνQL der gesamte effektive
Parallelwiderstand errechnet. Die bestimmten Werte lagen Größenordnungen unter
dem Parallelwiderstand des freien Resonators von 550 MΩ, womit sie als Eingangswiderstand des Verstärkers angenommen werden können und keine Berechnung auf
Grund der Parallelschaltung des Widerstands des freien Resonators mit eben dem
Eingangswiderstand des Verstärkers vonnöten ist.
Die aus den 3dB-Breiten bestimmten Werte Rmess stellen noch nicht den Widerstand Rin gemäß Abbildung 4.19 dar, sondern den gesamten Widerstand aus
Reihenschaltung von Koppelkapazität CC und Parallelschaltung aus Rin und Eingangskapazität Cin . Somit errechnet sich Rin gemäß des Spannungsteilers aus beiden
Kapazitäten aus dem gemessenen Wert nach
Rin =
CC
CC + Cin
2
· Rmess = α2 · Rmess
(4.47)
Die Abkopplung ist dabei abhängig von den gewählten Arbeitspunkten, da Cin
wie in Abschnitt 4.5.6 variiert. Für verschiedene Arbeitspunkte sind die Ergebnisse
in Abbildung 4.21 dargestellt.
71
4 Der kryogene Verstärker
6
S p a n n u n g a n G a te 2 (V )
5
0
-0 ,5
-0 ,9
-1 ,2
E i n g a n g s w i d e r s t a n d ( M Ω)
-0 ,7
-1 ,0
4
3
2
1
0
-0 ,7
-0 ,6
-0 ,5
-0 ,4
S p a n n u n g a n G a te 1 (V )
Abbildung 4.21: Eingangswiderstand in kryogener Umgebung bei verschiedenen Arbeitspunkten des Verstärkers.
Im interessanten Bereich, in dem der Verstärker arbeitet, zwischen -0,55 und 0,65 V an Gate 1, zeigt der Eingangswiderstand eine starke Abhängigkeit der Spannungseinstellung am oberen Kaskoden-FET, Gate 2. Bei geringen Spannungen bis
ca. -0,7 V liegt Rin unter oder knapp bei 2 MΩ. Mit weiter steigender negativer Spannung lassen sich Werte zwischen 3 und 4 MΩ erzielen. Analog zur Eingangskapazität
in Abschnitt 4.5.6 lässt sich dieses Verhalten durch die Arbeitsweise der Kaskode
erklären. Im Bereich ab ca. -0,9 V befindet sich der obere Kaskoden-FET in einem
Arbeitsbereich, der den Miller-Effekt unterdrückt. Hier ist die Kopplung des Eingangs
an das verstärkte Ausgangssignal nach den beiden Eingangs-FETs also geringer. Wie
in Abschnitt 4.3 erklärt, bedeutet eine geringere Millerkapazität, dass am Eingang
ein höhere Widerstand gegen Masse zu sehen ist. Nach diesen Messwerten ist also
ein Betrieb im Bereich ab -0,9 V angebracht, was die Daten zur Eingangskapazität
bestätigt.
Im Bereich einer funktionierenden Kaskodenschaltung zeigt der Eingangswiderstand einen abfallenden Verlauf von niedrigen Spannungen zu höheren Spannungen
72
4.5 Experimentelle Ergebnisse
an Gate 1 hin. Dies ist dadurch zu erklären, dass eine höhere Gate 1 - Spannung den
leitenden Kanal in den Eingangs-MESFETs weiter abschnürt und diese eine höheren
Gate-Drain-Widerstand RGD bereitstellen. Das wiederum führt zu einem Abfall des
am Eingang zu sehenden Eingangswiderstandes Rin , was in Kapitel 4.3 bereits gezeigt wurde und in der folgenden genaueren Ausarbeitung genauer untersucht und
quantifiziert wird.
4.5.8 Stromrauschen
Das Stromrauschen des Verstärkers ist eine wichtige Komponente des Detektors.
Mit dem Teststandresonator (vgl. Kapitel 4.5.5) steht auch ein hilfreiches Werkzeug zur Verfügung, das Stromrauschen in des Verstärkers zu charakterisieren. Dazu
wird der selbe Messmechanismus wie zur Messung des Spannungsrauschens verwendet (Abbildung 4.13). Nach Gleichung 4.28 werden hohe Quellwiderstände benötigt.
Die Verwendung des Resonators gewährleistet dies durch seinen Parallelwiderstand
von 550 MΩ, die sich durch Ankopplung des Verstärkers allerdings noch verringert,
wie im Kapitel 4.5.7 beschrieben. Im gemessenen Gesamtrauschspektrum sind nun
die Beiträge von thermischen Spannungsrauschen des Resonators und Stromrauschen
des Verstärkers zu trennen. Eine Messung im kryogenen Bereich ist sinnvoll, da damit
der thermische Rauschanteil erniedrigt wird.
Damit der Parallelwiderstand Rp des Resonators nicht zu stark erniedrigt wird,
wurde vor die auf die Platine gelötete 27 pF-Kapaziät noch eine weitere Kapazität
von 0,8 pF gesetzt und der Verstärker hierüber an den Resonator gekoppelt. die neue
Koppelkapazität beträgt dann nach der Reihenschaltung beider Bauteile
CC,2 =
Dadurch wird gemäß α =
1
1
+
27pF
0, 8pF
CC
CC +Cin
≈ 0, 8pF
(4.48)
eine geringere Abkopplung erreicht, die aber
noch von der Eingangskapazität und damit dem gewählten Arbeitspunkt abhängt.
Im Experiment konnten somit Güten im Bereich von 800 bis 1000 und damit effektive
Parallelwiderstände Rp von 12 bis 16 MΩ erreicht werden, die als Quellrauschwiderstände dienen.
Die Messung des Rauschspektrum erfolgte wiederum mit dem Sample-Detektor
des in Kapitel 4.5.4 beschriebenen FSP. Das Stromrauschen ergibt sich dann zu
1
in =
Rp
s
e2ges − e2F SP ·
1
G2Amp
− 4kB T Rp − e2n
(4.49)
73
4 Der kryogene Verstärker
Der lineare Verstärkungsfaktor GAmp muss aus vorherigen Messungen übernommen werden, die Bestimmung von Rp erfolgt über die 3dB-Breite. Es muss noch
beachtet werden, dass nicht das gesamte thermische Spannungsrauschen des Resonators tatsächlich am Eingang des Verstärkers anliegt. Auf Grund der Spannungsteilung
zwischen Koppelkondensator und Eingangskapazität erniedrigt sich dieses um den
bekannten Kopplungsfaktor α =
CC
CC +Cin
mit der jetzt modifizierten Koppelkapazität
CC,2 =0,8pF. Gleichung 4.49 wird damit zu
1
in =
Rp
s
e2ges − e2F SP ·
1
G2Amp
− 4kB T Rp α2 − e2n
(4.50)
Die Hauptunsicherheit bei der Bestimmung resultiert aus dem Term des thermischen Spannungsrauschens. Insbesondere die genaue Ermittlung der Temperatur des
Resonators war nicht möglich. Zur Messung war ein Temperatursensor direkt an der
kalten Stufe des Pulse Tubes installiert, ein weiterer am unteren Ende des Resonatorgehäuses. Über den Resonator war somit ein Temperaturanstieg von 2,7 K oben
hin zu 4,3 K unten zu verzeichnen. Zur Berechnung des Stromrauschens wurden
4 K angenommen, wie sie auch im Proton-Experiment herrschen. Die ermittelten
Werte stellen somit eher Richtwerte für die Größenordnung des Stromrauschens dar.
Es wurden Messungen im Bereich von -0,55 bis -0,65 V an Gate 1 vorgenommen,
während Gate 2 zwischen -0,2 und -1,2 V variiert wurde. Dabei ergaben sich Werte
zwischen 3 und 9
√f A .
Hz
Am vorgesehenen Arbeitspunkt mit der höchsten Verstär-
kung und einer im Vergleich annehmbaren Eingangsimpedanz, Gate 1 = -0,6V, Gate
2 = -1,0V, ergab sich ein Stromrauschen von 6
√f A .
Hz
Damit kann auch die Rauschtemperatur des Verstärkers beziffert werden. Nach
Gleichung 4.17
T =
e2n + i2n Rp
4kB Rp
ergibt sich bei einem Spannungsrauschen von 0,3 √nV
und einem effektiven ParalHz
lelwiderstand des gesamten Nachweissystems von 4 MΩ wie in den vorherigen Tests
realisiert eine Rauschtemperatur von 2,6 K. Dies ist insbesondere auf den geringen
Wert des Parallelwiderstands zurückzuführen. Bei optimaler Impedanztransformation Ropt =
en
in
= 50 kΩ ergäbe sich T = 0,07 K. Für einen Resonator wie den im
Teststand verwendeten mit einem Parallelwiderstand von 550 MΩ würde dies einen
Kopplungsfaktor α = 0,01 bedeuten.
74
4.6 Untersuchung des Eingangswiderstands
4.6 Untersuchung des Eingangswiderstands
Der geringe Eingangswiderstand des Verstärkers stellt ein echtes Problem dar. Die
hohe Güte des im Experiment verwendeten Resonator wird stark bedämpft, womit
zum Nachweis nur noch ein geringer Anteil des Parallelwiderstands zur Verfügung
steht. In den folgenden Abschnitten wird das Zustandekommen des Eingangswiderstands untersucht und Ansätze für Verbesserungen herausgearbeitet.
4.6.1 DC-Eingangswiderstand
Das über den Koppelkondensator eingespeiste Signal liegt über die intrinsischen ohmschen Gate-Source-Widerstände RGS der beiden Eingangs-FETs gegen Masse. Eine
mögliche Ursache für einen geringen Eingangswiderstand ist also, dass RGS im Bereich der gemessenen Werte liegt. Ebenso ist eine endliche ohmsche Verbindung über
Verunreinigungen der Platine denkbar.
Zur Untersuchung wurde der Gate-Anschluss der Eingangs-FETs bei Raumtemperatur direkt an eine Gleichspannungsquelle angeschlossen. Der Drain-Anschluss an
die nachfolgende Elektronik wurde unterbrochen. Die Spannung wurde variiert, während mit einem Amperemeter der fließende Strom gemessen wurde. Dieser extrem
simpel gestaltete Messaufbau gestaltete sich schwieriger als erwartet. Der extrem hohe Widerstand in den FETs bewirkte einen so geringen Strom, dass Messungen mit
gewöhnlichen Tischmultimetern nicht möglich waren. Auch die Verwendung von 50
MΩ-Widerständen als Shunts brachte keinen Erfolg. Schließlich gelang eine Messung
mittels eines Piko-Amperemeters. In Abbildung 4.22 sind zunächst die Kennlinien
für einen FET bzw. beide FETs auf der Platine zu sehen.
Die Kennlinien zeigen das typische Verhalten einer Diode. In Durchlassrichtung
steigt der Strom schnell mit ansteigender Spannung an. In Sperrrichtung, wie sie bei
negativer Spannung am Gate-Anschluss vorliegt, fließt nur ein sehr geringer Strom.
In der Abbildung ist die unterschiedliche Skalierung der y-Achse im positiven und
negativen Bereich zu beachten. Bei dem Gate-Anschluss der MESFETs handelt es
sich um einen Metall-Halbleiter-Übergang, einen sogenannten Schottky-Kontakt, der
ähnliche Eigenschaften wie ein p-n-Übergang einer Halbleiterdiode aufweist.
Qualitativ ist ebenfalls erkennbar, dass bei zwei installierten FETs ein größerer
Strom fließt. Sollte der Gate-Source-Widerstand der FETs die einzige DC-Verbindung
zwischen Signaleingang und Masse sein, ist eine Verdopplung des Stroms zu erwarten,
was mit den Messwerten in Einklang steht.
Interessant ist der Wert des tatsächlichen ohmschen Widerstands zwischen Gate
75
4 Der kryogene Verstärker
1 2
1 0
2 F E T s
1 F E T
8
S tro m
p o s itiv e y - R ic h tu n g : m A
n e g a tiv e y - R ic h tu n g : n A
6
4
2
0
-2
-4
-6
-8
-1 0
-5
-4
-3
-2
-1
0
1
S p a n n u n g a n G a te 1 (V )
Abbildung 4.22: Kennlinien des Gate-Source-Widerstands der Eingangs-FETs. Zur
Messung eines einzelnen FETs wurde der zweite von der Platine entfernt. Zu beachten ist die unterschiedliche Skalierung der y-Achse.
und Source. Aus den angelegten Spannungen und gemessenen Strömen ermittelt sich
dieser gemäß
RGS =
UGS
IGS
(4.51)
In Abbildung 4.23 ist dies für beide FETs einzeln auf einer Testplatine dargestellt.
Zusätzlich ist der theoretische Widerstand bei Parallelschaltung beider Gate-SourceWiderstände verzeichnet. Zum Vergleich ist schließlich noch der tatsächlich ermittelte Widerstand bei Installation beider FETs gleichzeitig auf der Verstärkerplatine
angegeben.
Es ist erkennbar, dass die tatsächlich gemessenen Werte auf die Parallelschaltung
der beiden unabhängig ermittelten einzelnen Gate-Source-Widerstände zurückgeführt werden können. Somit kann eine Gleichstromkontakt über die Platine ausgeschlossen werden.
Der gemessene Gleichstrom-Eingangswiderstand beider FETs auf der Verstärkerplatine bewegt sich bei den betrachteten Spannungen im Bereich eines GΩ. Jedoch
76
4.6 Untersuchung des Eingangswiderstands
8
oberer FET auf Testplatine
unterer FET auf Testplatine
beide FETs auf Verstärkerplatine
Parallelschaltung der Widerstände
Gate-Source-Widerstand (GΩ)
7
6
5
4
3
2
1
0
-4 ,0
-3 ,5
-3 ,0
-2 ,5
-2 ,0
Spannung an Gate 1 (V)
-1 ,5
-1 ,0
Abbildung 4.23: DC-Widerstand der Gate-Source-Strecke der Eingangs-FETs. Beide
FETs wurden einzeln auf einer Testplatine untersucht sowie zusammen auf der Platine des Verstärkers. Zum Vergleich der resultierende
Widerstand bei Parallelschaltung der beiden Widerstände aus den
Einzelmessungen
steigt er zu niedrigen Spannungen hin deutlich an. In diesem interessanten Bereich
zwischen -1 und 0 V, der ja auch den Bereich der Verstärkung erhält, war eine genaue
Messung nicht möglich, da die geringen Ströme mit dem Piko-Amperemeter nicht reproduzierbar aufgenommen werden konnten. Wichtig für den Eingangswiderstand,
den das Signal sieht, ist jedoch der differentielle Eingangswiderstand
RGS,dif f =
dUGS
uGS
=
dIGS
iGS
(4.52)
also die Steigung an der Stelle der als Arbeitspunkt gewählten Spannung. Die
Kleinbuchstaben u und i beschreiben in der Elektronik kleine Änderungen der Werte, wie sie durch das auszwertende Signal gegeben sind. Um den differentiellen DCEingangswiderstand zu quantifizieren, wurde der negative Spannungsbereich aus Abbildung 4.22 für beide FETs auf der Verstärkerplatine genauer untersucht. Abbildung
77
4 Der kryogene Verstärker
4.24 zeigt die aufgenommenen Messwerte und eine daran angepasste polynomische
Kurve der Form I(U ) = a · U 3 + b · U 2 , also eine Beschreibung mit einem Stromfluss
von 0 A für eine angelegte Spannung von 0 V und ohne Steigung an dieser Stelle.
0
Strom (nA)
-2
-4
-6
2 FETs auf Verstärkerplatine
-8
-1 0
-4
-3
-2
-1
Spannung an Gate 1 (V)
0
Abbildung 4.24: Kurvenanpassung an den Gate-Source-Widerstand der EingangsFETs zur Ermittlung des differentiellen Eingangswiderstands. Ein
Polynom der Form I(U ) = a · U 3 + b · U 2 wurde verwendet.
Diese Anpassung kann nur eine sehr rohe Abschätzung des differentiellen Eingangswiderstands liefern, da insbesondere im interessanten Bereich zwischen -1 und 0 V
keine Daten aufgenommen worden konnten. Auch die anderen Datenpunkte ließen
sich in mehreren Wiederholungen der Messungen nur auf etwa 20% genau reproduzieren. Die ermittelte Anpassung liefert die Werte a ≈ 0, 07 und b ≈ −0, 27. Exemplarisch lässt sich damit der Wert für eine Arbeitsspannung von -0,6 V berechnen.
dI nA
dU (−0,6V ) ≈ 0,4 V und damit
Rdif f (−0, 6V ) ≈ 2, 5GΩ
Dieser Wert liegt Größenordungen über den in Abschnitt 4.5.7 für den Eingangswiderstand ermittelten Werten um 4 MΩ. Auch mit dieser sehr groben Abschätzung
78
4.6 Untersuchung des Eingangswiderstands
lässt sich demnach feststellen, dass der niedrige Eingangswiderstand des Verstärkers
nicht auf eine niederohmige Gleichstrom-Kopplung zwischen Eingang und Masse zurückzuführen ist.
4.6.2 Modell zur kapazitiven Kopplung zwischen Gate und Drain der
EingangsFETs
Die Ursache sowie mögliche Verbesserungsansätze des Problems des geringen Eingangswiderstandes wird in diesem Abschnitt durch ein Modell zur kapazitiven Kopplung des Ausgangs der Eingangs-FETs an den Signaleingang untersucht. Dabei ist
die Gate-Drain-Kapazität CGD , wie sie in Abbildung 4.6 in Kapitel 4.3 dargestellt
ist, zentral. Über sie koppeln die nachfolgenden Bauteile an den Eingang des Verstärkers, und eine hohe ohmsche Last am Drain-Anschluss verursacht eine niedrige
ohmsche Eingangsimpedanz am Gate gegen Masse.
Zur Untersuchung der Eingangsimpedanz auf diese Weise wurde ein Modell des
Verstärkers entwickelt, das in Abbildung 4.25 dargestellt ist.
Anschluss,Drain
1,μF,
150,Ω
Zum,Drain
Sourcefolger
Anschluss,Drain
IDrain
Rwork
1000,Ω
Zum,Anschluss
Gate,Sourcefolger
1,μF,
150,Ω
IDrain,SF
10,nF
Zu,Anschluss
Gate,2
Rwork,,,
RDS
100,MΩ
CGD
Zu,Anschluss
Gate,1
Signal
Signal
Abbildung 4.25: Modell zur Untersuchung des Eingangswiderstands auf Grund der
Gate-Drain-Kapazität. Genauere Beschreibung im Text.
Links ist der für das Modell wesentliche Teil des Verstärkers dargestellt, dessen
gesamte Schaltskizze Abbildung 4.7 entnommen werden kann. Das Wechselstromsignal aus dem Nachweiskreis liegt an den Gate-Anschlüssen der Eingangs-FETs. Über
deren Gate-Drain-Kapazität CGD koppelt es an die am Drain-Anschluss anliegenden
79
4 Der kryogene Verstärker
Bauteile. Diese werden durch den gemeinsamen Drain-Source-Widerstand RDS beider Eingangs-FETs gegen Masse sowie den Arbeitswiderstand Rwork dargestellt. Der
Drain-Source-Widerstand des oberen Kaskoden-FET wird dabei zunächst vernachlässigt, kann aber bei der Auswertung des Modells in Rwork mit aufgenommen werden. Oberhalb des Arbeitswiderstandes liegt das Signal über eine 1 µF-Kapazität
gegen Masse, was im Vergleich zu den anderen beteiligten Widerständen einen zu
vernachlässigenden Widerstand für den Wechselstrom ergibt. Im niedrigen MHzBereich, in dem die Signale mit dem Testresonator untersucht werden, entspricht er
etwa 0,01 Ω. Damit liegt das Eingangssignal über die Gate-Drain-Kapazität CGD
und in Reihe dazu die Parallelschaltung von Rwork und RDS gegen Masse. Dies ist
links in Abbildung 4.26 zu sehen.
RDS
Rwork
CGD
Rin
Cin
Signal
Signal
Abbildung 4.26: Impedanztransformation beim Modell zum Eingangswiderstand
Über eine Impedanztransformation kann dann errechnet werden, welche Größen
ein ohmscher Widerstand und parallel dazu eine Kapazität haben müssen, wenn
sie direkt am Eingang gegen Massen geschaltet werden. Dies entspricht genau der
Eingangskapazität und dem zu untersuchenden Eingangswiderstand. Für die Impedanztransformation gilt
Re[
1
−1
−1 −1
−1
+ Rwork
+ RDS
] = Re[iωCin + Rin
]
iωCGD
(4.53)
Im[
1
−1
−1 −1
−1
+ Rwork
+ RDS
] = Im[iωCin + Rin
]
iωCGD
(4.54)
sowie
80
4.6 Untersuchung des Eingangswiderstands
Damit steht ein Modell zur Verfügung, mit dem der Eingangswiderstand Rin aus
dem Aufbau des Verstärkers hergeleitet werden kann. Unbekannte sind dabei die
Größe der Gate-Drain-Kapazität und die Größe des Drain-Source-Widerstandes RDS .
RDS wurde über die Messung des Drainstromes IDrain bestimmt. Als Gleichstrom
fließt dieser zuerst über einen 150 Ω-Widerstand. Anschließend fließt ein Teil in Richtung des Drain-Anschlusses des Sourcefolgers ab. Der verbliebene Strom schließlich
läuft zunächst über den Arbeitswiderstand Rwork und dann über den Gate-DrainWiderstand der Eingangs-FETs RDS . Aus der Kenntnis des Stroms über diese beiden
letzten Widerstände sowie der anliegenden Spannung können die Widerstände berechnet werden. Der am Sourcefolger abfließende Strom IDrain,SF wurde über das
Verhältnis von Spannung und Widerstand am Eingang des Netzwerkanalysators berechnet, an dem der Source-Anschluss des Sourcefolger anliegt.
Die Widerstände auf der Strecke zwischen Drain-Anschluss des Sourcefolgers und
Source-Anschluss der Eingangs-FETs, der auf Massen liegt, berechnen sich dann
gemäß
RStrecke = Rwork + RDS =
UStrecke
UDrain − IDrain · 150Ω
=
IStrecke
IDrain − IDrain,SF
(4.55)
Die Drain-Spannung wurde auf 2 V belassen und nicht verändert. In Abbildung
4.27 ist die Abhängigkeit des Drain-Source-Widerstandes der Eingangs-FETs in Abhängigkeit der Spannung an Gate 1 dargestellt.
Mit steigender negativer Spannung bis etwa -0,6 V ändert sich der Drain-SourceWiderstand zunächst kaum und liegt im Bereich von 1 kΩ. Ab dort ist ein steiler
werdender Anstieg zu verzeichnen, der im Bereich von -0,8 V über 100 kΩ erreicht.
Dieses Verhalten ist durch den inneren Aufbau eines MESFETs zu erklären. Mit
steigender negativer Gate-Spannung bildet sich eine breitere Raumladungszone um
den Schottky-Übergang, womit nur noch ein kleinerer Teil des Kanals zu elektrischen
Leitung zur Verfügung steht (siehe auch Kapitel 4.1).
Die Ermittlung der Gate-Drain-Kapazität CGD erfolgte über den Vergleich der
aus den oben beschriebenen Messungen ermittelten Werten für Rin mit den aus der
gemessenen Güte des Resonators bestimmten. Letztere wurden noch über die Abkopplung durch Koppelkapazität und Eingangskapazität in die Werte umgerechnet,
wie sie direkt am Eingang des Verstärkers gegen Masse anliegen müssen, um den entsprechenden gesamten effektiven Parallelwiderstand Rp zu erreichen (vgl. Abschnitt
4.5.7). Mittels Variation des Wertes der Gate-Drain-Kapazität CGD in den Modellrechnungen wurde dann das Modell an die tatsächlich gemessenen Werte angepasst.
81
1 0 0
D r a in - S o u r c e - W o d e r s ta n d R
D S
( k Ω)
4 Der kryogene Verstärker
1 0
1
-0 ,8
-0 ,6
-0 ,4
-0 ,2
0 ,0
S p a n n u n g a n G a te 1 (V )
Abbildung 4.27: Drain-Source-Widerstand der Eingangs-FETs in Abhängigkeit der
Spannung an Gate 1. Mit steigender negativer Spannung nimmt der
Widerstand zu, wie es bei MESFETs zu erwarten ist.
Zusätzlich ließ das Modell noch zu, den Arbeitswiderstand Rwork anzupassen, um
einen möglichen Einfluss des Gate-Drain-Widerstands des oberen Kaskoden-FETs
einfließen zu lassen. Abbildung 4.28 zeigt das Ergebnis der Anpassung. Die Messung
wurde bei einer Gate 2-Einstellung von -1,0 V durchgeführt, da hier durch die Kaskodenschaltung eine geringe Millerkapazität und damit ein hoher Eingangswiderstand
vorliegt.
Die in der Abbildung dargestellten Modellwerte erhält man bei einem CGD von
2,45 pF. Der Arbeitswiderstand Rwork wurde bei 1 kΩ belassen. Im Bereich bis etwa
-0,4 V an Gate 1, in dem keine Verstärkung vorliegt, stimmen Modell- und Messwerte in sehr gutem Maße überein. Der Verlauf lässt sich damit durch das Modell
erklären. Im verstärkenden Bereich, der durch den Wert der Verstärkung (in linearen
Einheiten) von mehr als 1 in der Abbildung eingetragen ist, ergibt sich eine Abweichung der Messwerte vom theoretisch erwarteten Verlauf, die tatsächlich gemessenen
Werte liegen unter denen des Modells. In das Modell geht noch nicht die Rückkopp-
82
4.6 Untersuchung des Eingangswiderstands
5
5
4
4
Messwerte
Modell
Verstärkung (linear)
Verstärkung (linear)
6
Eingangswiderstand (MΩ)
6
3
2
1
1
0
0
2
3
-0 ,8
-0 ,6
-0 ,4
-0 ,2
Spannung an Gate 1 (V)
0 ,0
Abbildung 4.28: Modellanpassung an Messwerte zur Bestimmung der Gate-DrainKapazität CGD der Eingangs-FETs. Die Modellwerte entsprechen
einer Ankopplung des Drain-Source-Widerstandes RDS über CGD
an den Eingang des Verstärkers. Die Messung wurde bei einer Gate
2-Einstellung von -1,0 V durchgeführt. Der ermittelte Wert betrug
CGD = 2,45 pF.
lung des Ausgang auf Grund der Steilheit gm der FETs ein. Tatsächlich lässt sich
diese Abweichung mit der Einführung eines Rückkopplungs-Verstärkungsfaktor von
GF B ≈ -0,08 erklären. Damit gilt dann Rin,gemessen = Rin,theoretisch · GF B · GA mit
linearer Verstärkung GA des Verstärkers [d’U03]. Das entspricht einer Modifikation
der Temperatur des Teilchens um 8% auf Grund der Rückkopplung.
Der Wert der Gate-Drain-Kapazität ist wesentlich höher als erwartet. Laut Datenblatt der NEC NE25139 -Eingangs-FETs besitzen sie eine Gate-Drain-Kapazität
von 0,02 pF1 . Auch Messungen zur Untersuchung ihrer Eignung ergaben mit 0,03 pF
einen Wert in dieser Größenordung [Ulm11]. Bei Parallelschaltung von zwei FETs
sollte sich der Wert der Gesamtkapazität zwischen Gate und Drain verdoppeln. Auf
Grund dieser Messungen und ihres geringen Spannungsrauschens waren sie für die
1
http://pdf1.alldatasheet.com/datasheet-pdf/view/93864/NEC/NE25139.html
83
4 Der kryogene Verstärker
Konstruktion des Verstärkers ausgewählt worden. Aus den Messungen ergibt sich
jedoch, dass in dem gewählten Design und der technischen Ausführung des vorliegenden Verstärkers die Kopplung zwischen Gate und Drain etwa um den Faktor
50 größer ist. Auch bei Auswechseln eines FETs änderte sich das Ergebnis nicht,
zumindest in der vorliegenden Charge lässt sich mit den FETs offenbar kein besserer Wert erzielen. Eine weitere Möglichkeit für ein hohes CGD wäre eine kapazitive
Kopplung außerhalb der FETs über die Platine. Dies kann für den untersuchten konkreten Aufbau des Verstärkers nicht ausgeschlossen werden. Eine Vergleichsmessung
bei Wegnahme eines Eingangs-FETs kann jedoch Hinweise geben.
In Abbildung 4.29 sind die Messwerte für den Eingangswiderstand am Verstärker
Rin für einen und für zwei Eingangs-FETs angegeben. Als x-Achse wurde der Drainstrom IDrain gewählt, der über die konstant gehaltene Drainspannung von 2 V Aufschluss über den Gesamtwiderstand RStrecke = Rwork + RDS liefert. Gleicher Strom
bedeutet also, dass insbesondere der Drain-Source-Widerstand RDS den gleichen
Wert hat. Für die Vergleichsmessung bezogen auf die Gate-Drain-Kapazität CGD
ist dies wichtig, damit entschieden werden kann, ob die Veränderung des Eingangswiderstandes auf die Änderung von CGD bei Abnehmen eines FETs zurückgeführt
werden kann.
Die Messung wurde mit einer Gate 2-Spannung von -0,7 V durchgeführt. Qualitativ ist zu erkennen, dass bei Herabnehmen eines FETs eine ungefähre Verdopplung
des Eingangswiderstandes zu sehen ist. Dies entspricht der Annahme, dass die GateDrain-Kapazität bei den Eingangs-FETs durch Entfernen eines FETs halbiert wird.
Damit ist die Kopplung der ohmschen Last am Drain-Anschluss nur noch halb so
groß, was eine entsprechende Heraufsetzung des zwischen Gate und Masse sichtbaren Eingangswiderstands bewirkt. Auf Grund dieser Messung scheinen die gewählten
FETs die hohe Kopplung zu verursachen. Dieses Ergebnis ist nicht zu erwarten gewesen. Der von S. Ulmer ebenfalls mit NE25139 -FETs konstruierte Verstärker zeigte diese hohe Gate-Drain-Kapazität nicht. Hier konnte der Eingangswiderstand auf
eine Kopplung der Last am Ausgang über eine Millerkapazität von 0,03 pF zurückgeführt werden [Ulm11]. Eine zusätzliche kapazitive Kopplung zum Beispiel über die
Lötstellen der FETs oder das Platinenmaterial kann aber weiterhin nicht endgültig
ausgeschlossen werden.
Bei Durchführung der Messung mit nur einem Eingangs-FET bot sich auch die
Möglichkeit, die resultierende Eingangskapazität vergleichend darzustellen. Dies ist
in Abbildung 4.30 zu sehen. Die Messung erfolgte bei einer Gate 2-Spannung von
84
4.6 Untersuchung des Eingangswiderstands
8
7
2 E in g a n g s - F E T s
1 E in g a n g s - F E T
E i n g a n g s w i d e r s t a n d ( M Ω)
6
5
4
3
2
1
0
0 ,2
0 ,4
0 ,6
0 ,8
1 ,0
D r a in s tr o m
1 ,2
1 ,4
1 ,6
(m A )
Abbildung 4.29: Vergleich des Eingangswiderstandes für einen und zwei EingangsFETs. Als x-Achse ist der Drainstrom und damit die Vergleichsgröße
RStrecke = Rwork + RDS gewählt, damit der Unterschied auf Grund
der Veränderung von CGD bei Herabnehmen eines FETs zu sehen
ist. Bei Halbierung von CGD bei einem Eingangs-FET gegenüber
zwei Eingangs-FETs zeigt sich qualitativ etwa eine Verdoppelung
des Eingangswiderstandes. Die Aufnahme erfolgte für eine Gate 2Spannung von -0,7 V.
-0,9 V.
Deutlich zu erkennen ist, dass das Herabnehmen eines FETs die Eingangskapazität
reduziert. Ganz analog zum Eingangswiderstand, der erniedrigt wird, ist das durch
die schwächere Ankopplung der ohmschen Last am Drain-Anschluss zu erklären. Die
gemessenen Kapazitätswerte lassen sich quantitativ erklären, indem von einer zusätzlichen kapazitiven Kopplung im Bereich von 1 pF zwischen Gate-Anschluss der
Eingangs-FETs und Masse über die Platine ausgegangen wird. Darauf addieren sich
dann die durch die FETs zugefügten Kapazitäten, die beide im gleichen Bereich liegen. Für die hier präsentierte Messung bei einer Gate 2-Spannung von -0,9 V beträgt
die pro FET zugefügt zusätzliche Eingangskapazität etwa 4 pF im Bereich der Gate
85
4 Der kryogene Verstärker
8
7
Eingangskapazität (pF)
6
5
4
3
1 Eingangs-FET
2 Eingangs-FETs
2
1
0
-0 ,9
-0 ,8
-0 ,7
-0 ,6
-0 ,5
-0 ,4
Spannung an Gate 1 (V)
-0 ,3
-0 ,2
Abbildung 4.30: Vergleich der Eingangskapazität für einen und zwei Eingangs-FETs.
Die Werte sind erklärbar, indem man von einer kapazitiven Kopplung von etwa 1 pF über die Platine gegen Masse ausgeht, zu der
sich beide durch die Kopplung über CGD der FETs hinzugefügte
Kapazitäten addieren.
1-Spannung von -0,2 bis -0,5 V, danach nimmt sie etwas ab.
86
4.7 Zusammenfassung und Signal-Rausch-Verhältnis
4.7 Zusammenfassung und Signal-Rausch-Verhältnis
Mit den ermittelten Werten kann das Signal-Rausch-Verhältnis SNR berechnet werden, das die kritische Größe für den Einsatz des Verstärkers darstellt. Zunächst ist
hier noch eine Zusammenfassung der Ergebnisse der Messungen gegeben.
• Die Verstärkung ist mit über 10 dB und damit einem linearen Verstärkungsfaktor A1 von über 3 groß genug, dass das Rauschen der nächsten Verstärkerstufe
im Raumtemperaturbereich gemäß der Friisschen Formel keine Rolle spielt.
Der Verstärker selbst besitzt nach Gleichung 4.13 eine Rauschzahl F1 von 4,6
bei einem effektiven Parallelwiderstand des Nachweiskreises von 50 MΩ. Die
Rauschwahl F2 des ZFL als nachfolgende Stufe bei Raumtemperatur und ei2 −1
nem 50 Ω-Eingang beträgt 1,9 und ist damit gemäß Fges = F1 + FA
(Gleichung
1
4.14) für das Gesamtrauschen der Kette nicht ausschlaggebend.
• Die Leistungsaufnahme ist mit unter 7mW nur eine geringe Wärmelast für die
Kühleinheit
• Die Rauscheigenschaften konnten bestimmt werden. Im Bereich einer guten
Verstärkung betrug das Spannungsrauschen 0,3 √nV
. Dies ist eine deutliche
Hz
Verbesserung gegenüber dem aktuell eingebauten Verstärker mit einer Rauschleistung von 1,6
nV
√
.
Hz
Die Verbesserung ist neben der Parallelschaltung der zwei
Eingangs-FETs möglicherweise auch auf eine im Bezug auf das Rauschen gut
gefertigte Charge der Transistoren zurückzuführen. Das Stromrauschen konnte
mit Hilfe des Teststandresonators im Bereich zwischen 3 und 9 √fA
bestimmt
Hz
werden, unterliegt jedoch auf Grund der Messweise gewissen Unsicherheiten.
Für den gewählten Arbeitspunkt, an dem der Verstärker betrieben werden
sollte (Gate 1 = -0,6 V, Gate 2 = -0,9 V) ergab sich ein Stromrauschen von
. Für das Stromrauschen muss außerdem in Erwägung gezogen werden,
4 √fA
Hz
dass es bei Resonanzfrequenz des Teststandresonators, etwa 1,3 MHz und nicht
im beabsichtigten Arbeitsbereich für die axiale Frequenz des Teilchens von etwa 700 kHz gemessen wurde. Ein Anstieg der Rauschleistung zu niedrigeren
Frequenzen hin kann nicht ausgeschlossen werden.
• Die ermittelte Eingangskapazität des Verstärkers liegt für Bereiche mit geeigneter Gate 2-Einstellung im Bereich von 8 pF. Sie erhöht die Gesamtkapazität
des Nachweiskreises und erniedrigt damit dessen Resonanzfrequenz. Außerdem
hat sie einen Einfluss auf das Kopplungsverhältnis bei kapazitiver Ankopplung,
87
4 Der kryogene Verstärker
das aus dem Verhältnis von Koppelkapazität und Eingangskapazität gebildet
wird. Bei einem hohen Übersetzungsverhältnis in der Ankopplung sinkt der
Einfluss der Eingangskapazität auf den Gesamtnachweiskreis.
• Der Eingangswiderstand des Verstärkers liegt im günstigen Fall für eine geeignete Gate 2-Spannung knapp unter 3 MΩ. Der effektive Parallelwiderstand des
gesamten Nachweiskreises, der im Bereich einiger 100 MΩ liegt, würde somit
nur für eine schwache Abkopplung nicht merklich bedämpft werden. Eine hohe
Güte ist erforderlich für eine ausreichende Breite des Dips bei der Detektion
über die entsprechende Methode.
35
30
SNR HdBL
25
20
15
10
5
0
0.0
0.2
0.4
0.6
0.8
1.0
Abkopplung
Abbildung 4.31: Erwartetes Signal-Rausch-Verhältnis bei der Dip-Detektion in Abhängigkeit des Kopplungsfaktor α. Weitere Werte zur Modellrechnung siehe Text.
Das Signal-Rausch-Verhältnis zum Nachweis über die Dip-Methode (Abschnitt
3.3) ergibt sich gemäß Gleichung 3.29 zu
SN RDip
v
u
2
u
α2 R p
α2 R p
u 4kT
+
i2n α4 + e2n
R
R
u
1+α2 R p
1+α2 R p
t
in
in
=
e2n
Abbildung 4.31 zeigt das Signal-Rausch-Verhältnis in Abhängigkeit des Abkoppelfaktors α in logarithmischen Einheiten. Dabei wurden als Parallelwiderstand des
Teststandresonators Rp = 550 MΩ, als Eingangswiderstand des Verstärkers Rin =
88
4.7 Zusammenfassung und Signal-Rausch-Verhältnis
3 MΩ, als Spannungsrauschen en = 0,4 √nV
und als Stromrauschen in = 4 √fA
verHz
Hz
wendet. Die Temperatur wurde gemäß der Messungen am Teststand mit 3 K angenommen.
Das Signal-Rausch-Verhältnis zeigt ab einer Abkopplung von etwa α ≈ 0,2 keine weitere Verbesserung bei härterer Ankopplung, bei weicherer Ankopplung fällt es
jedoch deutlich ab. Zum Betrieb im Experiment sollte also eine Abkopplung von mindestens 0,2 gewählt werden. Am Teststandresonator konnte während der Messung des
Stromrauschens ein Test der Voraussage des Modells durchgeführt werden. Bei dem
gewählten 27 pF-Koppelkondensator und einer Eingangskapazität von 8,0 pF bei den
Testeinstellungen Gate 1 = -0,7 V und Gate 2 = -1,0 V betrug der Kopplungsfaktor
α = 0,77. Die Messung des Rauschspektrums ist in Abbildung 4.32 gegeben.
-7 5
Signalstärke in dBm
-8 0
-8 5
-9 0
S N R
-9 5
-1 0 0
-1 0 5
-1 1 0
0 ,9
1 ,0
1 ,1
1 ,2
1 ,3
1 ,4
Frequenz in MHz
1 ,5
1 ,6
1 ,7
Abbildung 4.32: Rauschspektrum des Teststandresonators. Hieraus kann das SignalRausch-Verhältnis SNR abgelesen werden. Für den gewählten Arbeitspunkt Gate 1 = -0,7 V und Gate 2 = -1,0 V ergibt sich ein SNR
von etwa 33 dB.
Tatsächlich ist hier ein SNR von etwa 33 dB ablesbar, wie es im Modell vorausberechnet wurde. Damit bestätigt sich auch die Annahme von in = 4 √fA
für diesen
Hz
Arbeitspunkt. Nach diesen Messungen ist der Verstärker bei entsprechender Abkopp-
89
4 Der kryogene Verstärker
lung also geeignet, ein hohes SNR zu liefern, was die Messung der Bewegungsfrequenz
des Teilchens erleichtert.
Eine weitere wichtige Kennziffer ist jedoch auch die Breite des Dips (vgl. Abschnitt
3.3), die mit dem effektiven Parallelwiderstand des gesamten Nachweiskreises skaliert
gemäß Gleichung 3.22
∆ν =
1 q 2 Rp
2π mD2
Hierzu muss der verbleibende effektive Parallelwiderstand Rp des Resonators betrachtet werden. Abbildung 4.33 zeigt diesen für den verwendeten Teststandresonator
mit seinem freien effektiven Parallelwiderstand 550 MΩ.
R_p HMegaohmL
500
400
300
200
100
0
0.0
0.2
0.4
0.6
0.8
1.0
Abkopplung
Abbildung 4.33: Effektiver Parallelwiderstand des Nachweiskreises gegen Ankopplung des Verstärkers. Zu härteren Ankopplungen hin nimmt der
Parallelwiderstand rapide ab und nähert sich dem Wert des Eingangswiderstand des Verstärkers Rin = 3 MΩ.
Bei einer Abkopplung von 0,2 beträgt der effektive Parallelwiderstand nur noch
56 MΩ und fällt danach weiter ab, bis er ab α ≈ 0,4 im Bereich des Eingangswiderstandes Rin =3 MΩ verbleibt. Hier ist also auch keine ausreichende Dipbreite zu
erwarten, welche in Abbildung 4.34 dargestellt sind. Die Werte für den effektiven
Elektrodenabstand D wurden aus Tabelle 3.1 übernommen. Es gelten die Werte
für eine Signalaufnahme an den Korrekturelektroden, wie sie auch im Experiment
geschieht [Ulm11].
90
4.7 Zusammenfassung und Signal-Rausch-Verhältnis
50.0
Dipbreite Hz
4,12 mm
7,60 mm
10.0
5.0
1.0
0.5
0.1
0.0
0.2
0.4
0.6
0.8
1.0
Abkopplung
Abbildung 4.34: Breite des Dips gegen Abkopplung des Verstärkers für verschiedene
effektive Elektrodenabstände. Die Graphen entsprechen von oben
nach unten D = 4,12 und D = 7,60 mm. Analog zum Abfall des
effektiven Parallelwiderstands in Abbildung 4.33 fällt die Dipbreite
zu starken Abkopplungen hin deutlich ab.
Die beiden oberen Graphen entsprechen den effektiven Elektrodenabständen D
= 4,12 und D = 7.60 mm und gelten für die Analyse- und die Präzisionsfalle zur
Aufnahme der axialen Frequenz an den Korrekturelektroden. Um eine Dipbreite von
1 Hz zu erreichen, sind bei den ersten beiden Werten Abkopplungen von höchstens
0,6 bzw. 0,3 nötig. Das SNR liegt dabei jeweils im Bereich von etwa 33 dB. Bei größerem D ist eine noch weichere Abkopplung erforderlich. In Abbildung 4.35 ist dies
anhand einer angenommenen Abkopplung von 0,2 zu sehen. Die Dipbreite folgt einem
1
-Gesetz
D2
und nimmt zu höheren effektiven Abständen und damit schwächeren
Ankopplungen an die Fallenwände deutlich ab. Für ein D von 20 mm ist so etwa nur
noch eine Dipbreite von knapp 0,6 Hz vorhanden. Um mindestens 1 Hz Dipbreite zu
erhalten, ist eine Abkopplung von α = 0,1 erforderlich. Hier ergibt sich ein SNR von
ca. 32 dB.
Ein solcher Nachweis kann den bisher installierten ersetzen. Er bietet ausreichende
Dipbreite bei den gegebenen Parametern des Experiments, ein hohes Signal-RauschVerhältnis und ein niedrigeres Rauschen.
Nach Abschnitt 3.4 kann auch das Signal-Rausch-Verhältnis für eine Bestimmung
der Bewegungsfrequenz des Teilchens über die Peak-Methode bestimmt werden. Da-
91
4 Der kryogene Verstärker
Dipbreite HHzL
8
6
4
2
5
10
15
20
Effektiver Elektrodenabstand HmmL
Abbildung 4.35: Breite des Dips gegen effektiven Elektrodenabstand D bei einer angenommenen Abkopplung von α = 0,2. Bei einem D von 20 mm ist
der Dip noch 0,56 Hz breit.
bei berechnet sich das SNR gemäß Gleichung 3.33 zu
SN RP2 eak
(IIon Rin Rp )2
#
2
i R Rin
4kT Rin Rp
e2n + n pRin
Rp +
+
Rin
="
Rp +
α2
Rp +
α2
Rin
α2
2
α2
Das SNR bei der Peak-Methode skaliert mit dem durch das schwingende Teilchen induzierten Ionenstrom IIon . Typischerweise liegt dieser im Bereich von 100
fA. Abbildung 4.36 gibt eine Übersicht über das erwartete SNR für verschiedene Ionenströme bei den aus den Messungen ermittelten Werten des Verstärkers, wie am
Anfang dieses Kapitels beschrieben.
Je nach Ionenstrom sind also SNR-Werte im Bereich zwischen 40 und 50dB zu
erreichen. Dies gilt allerdings nur für das Maximum des SNR, das bei den ermittelten Werten bei α ≈ 0,01 liegt. Bei dieser Konfiguration nimmt das Signal-RauschVerhältnis bei der Dip-Methode jedoch so stark ab (Abbildung 4.31), dass keine
Messung der axialen Frequenz des Teilchens im thermischen Gleichgewicht mehr
möglich ist.
Zusammenfassend gilt, dass der untersuchte Verstärker geeignet ist, in das Experiment installiert zu werden. Selbst bei einem angenommenen effektiven Elek-
92
4.7 Zusammenfassung und Signal-Rausch-Verhältnis
SNR dB
50
200 fA
45
150 fA
40
100 fA
35
50 fA
30
25
20
15
0.0
0.2
0.4
0.6
0.8
1.0
Abkopplung
Abbildung 4.36: Signal-Rausch-Verhältnis bei Peak-Detektion gegen Ankopplung des
Verstärkers. Es sind verschieden Ionenströme im Bereich von 50 bis
200 fA aufgetragen. Hohe Ströme bedeuten ein höheres SNR. Für
harte Ankopplungen nimmt das SNR ab und besitzt ein Maximum
bei α ≈ 0,01.
trodenabstand D = 20 mm, der weit über den im realen Experiment bestimmten
Abständen liegt, ist bei einer Dipbreite von 1 Hz ein Signal-Rausch-Verhältnis für
die Dip-Methode von etwa 32 dB zu erwarten. Für niedrigeres D ist eine schwächere
Ankopplung des Verstärkers möglich, um den effektiven Parallelwiderstand des Nachweiskreises weniger stark zu bedämpfen. Damit lässt sich eine noch höhere Dipbreite
erzielen. Das Gesamtrauschen des Verstärkers liegt deutlich unter dem des bisher
verbauten.
Als problematisch erweist sich der Eingangswiderstand des Verstärkers, der geringer
als erwartet ausfällt und damit die Güte des Nachweiskreises beschränkt. Dieser ist
im Experiment durch den Einsatz von supraleitenden Resonatoren, wie sie auch im
Teststand angewandt wurden, speziell für einen hohen effektiven Parallelwiderstand
von einigen 100 MΩ ausgelegt. Ein solcher wird auch für die effektive Kühlung mit
einer kleinen Kühlzeitkonstante τ =
mD2
Rp q 2
des Teilchens benötigt (Gleichung 3.14).
Auch hier ist durch eine entsprechende Wahl der Abkopplung mit Blick auf das
SNR eine Abwägung zu treffen, da bei schwächerer Ankopplung das SNR bei der
Dip-Methode absinkt. In der Präzisionsfalle ist ein effektiver Parallelwiderstand von
50 MΩ ausreichend.
93
5 Zusammenfassung und Ausblick
Ziel dieser Examensarbeit war der Aufbau und die Charakterisierung eines rauscharmen Verstärkers zur Messung der Bewegungsfrequenz eines einzelnen Protons in
einer Penningfalle. Beim Aufbau des Verstärkes konnten mannigfaltige Erfahrungen
in der mechanischen Handfertigung elektronischer Schaltungen und dem Planen und
Durchführen von gerätegestützten Messungen gemacht werden. Auch das Auffinden
und Ausmerzen nicht erwarteter Fehlerquellen, eine ständige Begleiterscheinung in
der Experimentalphysik, hatte einen großen Anteil an der Arbeit.
Alle wichtigen Parameter des Verstärkers konnten ermittelt werden und ihre Abhängigkeit von den Arbeitspunkteinstellungen dokumentiert und nachvollzogen werden. Der Verstärker bestätigte die Erwartung an ein niedriges Eingangsspannungsrauschen im Bereich von 300
pV
√
Hz
und liegt in diesem Wert deutlich unter dem
momentan verbauten Verstärker. Die Spannungsverstärkung im Bereich zwischen 10
und 13 dB ist ausreichend, die Leistungsaufnahme mit unter 7 mW erfreulich gering.
Als problematisch erwies sich der sehr geringe Eingangswiderstand des Verstärkers,
der die Güte des gesamten Nachweiskreises herabsetzt. Mit etwa 3 MΩ lag er deutlich unter den Erwartungen. Er konnte auf eine starke kapazitive Kopplung zwischen
Gate und Drain der Eingangs-FETs zurückgeführt werden.
Für die durch das Experiment vorgegebenen Parameter des effektiven Elektrodenabstandes bieten sich bei entsprechender Abkopplung Möglichkeiten, sowohl eine
ausreichende Dipbreite von mindestens 1 Hz als auch das oben genannte SNR zu
erreichen. Bei einem verbleibenden effektiven Parallelwiderstand des Nachweiskreises von 50 MΩ, was in der Präzisionsfalle ausreichend ist, ist der Verstärker geeignet, in das Proton-Experiment installiert zu werden. Er bietet eine Verbesserung
der bisher erreichten Rauscheigenschaften. Für andere Experimente mit ähnlicher
Nachweistechnik, die etwa mit Kupferresonatoren geringerer Güte arbeiten, ist der
vorliegende Verstärker darüber hinaus noch besser geeignet, da hier das Problem der
Bedämpfung der Güte verschwindet.
95
5 Zusammenfassung und Ausblick
Am Experiment selbst konnte letztes Jahr ein Meilenstein gefeiert werden. Zum
ersten Mal ist der Nachweis eines Spin-Flips in der Penningfalle gelungen. Die Messung erfolgte über die Bestimmung der Spin-Übergangsrate als Funktion der eingestrahlten magnetischen Hochfrequenz-Felder. Dabei konnte eine relative Genauigkeit
von 10−4 erreicht werden, was für eine entsprechende Messung an einem Antiproton bereits einen 10-mal genaueren als den bisher bekannten Wert ergäbe. Cricia
Rodegheri präsentiert diese Ergebnisse in [Rod20]. Ziel ist es, Spin-Quantensprünge,
die in der Präzisionsfalle angeregt wurden, nachzuweisen. Mit der dann möglichen
Präzision ließe sich eine Genauigkeit von 10−9 oder noch besser erreichen.
96
Literaturverzeichnis
[Agi06]
Agilent Technologies: Spectrum Analyzer Basics. Agilent Application
Note, 2006.
[Alo07]
Alonso Otamendi, J.: Development of an Experiment for UltrahighPrecision g-Factor Measurements in a Penning-Trap Setup. Doktorarbeit,
Johannes Gutenberg-Universität Mainz, 2007.
[Ame05] Ames, F., Bollen G. Delahaye P. Forstner-O. Huber G. Kester O. Reisinger K. Schmidt P.: Cooling of radioactive ions with the
Penning trap REXTRAP. Nucl. Instr. Meth. A, 538:17, 2005.
[Bro82] Brown, L. S., Gabrielse G.: Precision spectroscopy of a charged particle
in an imperfect penning trap. Physical Review A, 25(4):2423-2425, 1982.
[Bro86] Brown, L. S., Gabrielse G.: Geonium theory: Physics of a single electron or ion in a Penning trap. Rev. Mod. Phys., 58(1), 1986.
[Deh68] Dehmelt, H. G. und F. L. Walls: „Bolometric“ technique for the rf
spectroscopy of stored ions. Rev. Lett., 21:127, 1968.
[Deh87] Dehmelt, H.G., Van Dyck R. Schwinberg P.: New high-precision
comparison of electron and positron g factors. Phys. Rev. Lett. 59, 26-29,
1987.
[Deh88] Dehmelt, H. G.: New continous Stern-Gerlach effect and a hint of the
elementary particle. Z. Phys. D, 10:127, 1988.
[Dem00] Demtröder, W.: Experimentalphysik 3. Springer, 2000.
[d’U03] d’Urso, B., Odom B. Gabrielse G.: Feedback Cooling of a One-Electron
Oscillator. Phys. Rev. Lett 90, 2003.
[Fol86]
Folkes, P. A.: Characteristics and mechanism of 1/f noise in GaAs
Schottky barrier field-effect transistors. Appl. Phys. Lett., 48:344, 1986.
97
Literaturverzeichnis
[Fri44]
Friis, H.T.: Noise Figures of Radio Receivers. Proc. IRE, 32:419, 1944.
[Gab89] Gabrielse, G., Haarsma L. Rolston S.L.: Open-endcap Penning Traps
for High Precision Experiments. Int. J. Mass Spectrom. Ion Processes,
88:319, 1989.
[Gab99] Gabrielse, G., A. Khabbaz D. S. Hall-C. Heimann H. Kalinowsky
und W. Jhe: Precision Mass Spectroscopy of the Antiproton and Proton
Using Simultaneously Trapped Particles. Phys. Rev. Lett., 82:3198, 1999.
[Han08] Hanneke, D., Fogwell S. Gabrielse G.: New measurement of the
electron magnetic moment and the fine structure constant. Physical Review
Letters, 100(12):120801, 2008.
[Hil89]
Hill, W., Horowitz P.: The Art Of Electronics. Cambridge University
Press, 1989.
[HW03] Häffner, H., Beier T. Djekic S. Hermanspahn-N. Kluge H.J.
Quint W. Stahl S. Verdú J. Valenzuela T. und G. Werth: Double
Penning trap technique for precise g factor determinations in highly charged
ions. The European Physical Journal D-Atomic, Molecular, Optical and
Plasma Physics, 22(2):163-182, 2003.
[Jef93]
Jefferts, S.R., Heavner T. Hayes P. Dunn-G.H. Rev. Sci. Instrum.
64, 737, 1993.
[Jhe92]
Jhe, W., Phillips D. Haarsma L. Tan-J. Gabrielse G.: Cylindrical
penning traps and self-shielding superconducting solenoids for high precision
experi- ments. Physica Scripta, 46(3):264-267, 1992.
[Joh]
Johnson, J.: Thermal Agitation of Electricity in Conductors.
[Kel03]
Kellerbauer, A., K. Blaum G. Bollen F. Herfurth H.-J. Kluge
M. Kuckein E. Sauvan C. Schneidenberger und L. Schweikhard:
From direct to absolute mass measurements: A study of the Accuracy of
ISOLTRAP. Eur. Phys. J. D, 22:53, 2003.
[Kle75]
Kleppner, D., Phillips W. Cooke E.: Magnetic Moment of the Proton
in Bohr Magnetons. Phys. Rev. Lett. 35:1620, 1975.
98
Literaturverzeichnis
[Kra07] Kracke, H.: Entwicklung der kryogenen Nachweis-Elektronik zur Bestimmung der axialen Frequenz des Protons in einer Penning-Falle. Doktorarbeit, Johannes Gutenberg-Universität Mainz, 2007.
[Kre08] Kreim, S., J. Verdu K. Blaum H. Kracke Quint-W. Ulmer S.
Walz J.: Greens function calculation of electrostatic properties of open
Penning traps with arbitrary axial symmetry. New Journal of Physics 10
(2008) 103009 (23pp), 2008.
[Lüd57] Lüders, G., Zumino B.: Some consequences of tcp-invariance. Physical
Review, 106(2):385-386, 1957.
[Lee89]
Lee, A. T.: Broadband cryogenic preamplifiers incorporating GaAs MESFETs for use with low-temperature particle detectors. Phys. Rev. Lett.,
60:3315, 1989.
[Mar07] Marti, O., Plettl A.: Vorlesungsskript Physikalische Elektronik und
Messtechnik. Vorlesungsskript, 2007.
[Men92] Menke, H., Gundlach F. W.: Tschenbuch der Hochfrequenztechnik.
Springer, 1992.
[Mil12]
Miller, J.: Dependence of the input impedance of a three-electrode vacuum
tube upon the load in the plate circuit. Scientific Papers of the Bureau of
Standards 15, Nr. 351, 2012.
[Nyq]
Nyquist, H.: Thermal Agitation of Electric Charge in Conductors.
[Pas09] Pask, T., Barna D. Dax A. Hayano R.S. Hori-M. Horváth D.
Friedrich S. Juhász B. Massiczek O. Ono N. Sótér A. Widmann E.: Antiproton magnetic moment determined from HFS of p̄He+ .
Physics Letters B, 678(1), 2009.
[Qui93] Quint, W., Gabrielse G.: The magnetic moment of the antiproton. Hyperfine Interactions, 76: 379-380, 1993.
[Qui04] Quint, W., Alonso J. Djekic S. Kluge H.J. Stahl-S. Valenzuela
T. Verdú J. Vogel M. Werth G.: Continuous Stern-Gerlach effect
and the magnetic moment of the antiproton. Nuclear Inst. and Methods in
Physics Research, B, 214:207210, 2004.
99
Literaturverzeichnis
[Rod20] Rodegheri, C. C., Blaum K. Kracke H. Kreim S.-Mooser A.
Quint W. Ulmer S. Walz J.: An Experiment for the direct determination of the g-factor of a single proton in a Penning trap. New J. Phys.
14 063011, 1920.
[Sch26]
Schottky, W.: Small-Shot Effect And Flicker Effect. Phys. Rev., 28:74,
1926.
[Sch95]
Schwingenheuer, B. et al.: CPT Tests in the Neutral Kaon System.
Phys. Rev. Lett. 74, 4376-4379, 1995.
[Sch03]
Schiffel, R., Köhler A.: Werkbuch Hochfrequenz-Technik. FRANZIS,
2003.
[Sch06]
Schwarz, Rohde &: Betriebshandbuch FSP-13. www.rohde-schwarz.de,
2006.
[Sho38] Shockley, W.: Currents to conductors induced by a moving point charge.
J. Appl. Phys., 9:635, 1938.
[Spi06]
Spieler, H.: Semiconductor Detector Systems. Oxford University Press,
2006.
[Sta05]
Stahl, S., J. Alonso S. Djeki´c H.-J. Kluge-W. Quint J. Verd´u
und M. Vogel: Phase-sensitive measurement of trapped particle motions.
J. Phys. B: At. Mol. Opt. Phys., 38:297 to 304, 2005.
[Ste03]
Steffen, A.: Signale und Übertragung. Vorlesungsskript, 2003.
[Stu12]
Sturm, S.: The g-factor of the electron bound in
stringent test of bound state QED.
28 Si13+ :
The most
Dissertation, Johannes Gutenberg-
Universität Mainz, 2012.
[Tex01] Texas Instruments:
Op
Amp
Noise
Theory
and
Applications.
http://focus.ti.com/lit/ml/sloa082/sloa082.pdf, 2001.
[Ulm06] Ulmer, S.: Entwicklung des experimentellen Aufbaus zur Messung des
g-Faktors des Protons in einer Penning-Falle.
Doktorarbeit, Johannes
Gutenberg-Universität Mainz, 2006.
[Ulm11] Ulmer, S.: First Observation of Spin Flips with a Single Proton Stored
in a Cryogenic Penning Trap. Dissertation, Ruperto Carola-Universität
Heidelberg, 2011.
100
Literaturverzeichnis
[VD99]
Van Dyck, R. S., Farnham D. L.-Zafonte S. L. Schwinberg P. B.:
Ultrastable superconducting magnet system for a penning trap mass spectrometer. Review of Scientic Instruments, 70(3):1665-1671, 1999.
101
Eidesstattliche Erklärung
Hiermit versichere ich, Reinhard Heinke, dass ich die wissenschaftliche Prüfungsarbeit für die Erste Staatsprüfung für das Lehramt an Gymnasien selbstständig ohne
fremde Hilfe verfasst und keine anderen als die angegebenen Hilfsmittel verwendet
habe. Diese Erklärung schließt auch die im Internet zugänglichen Daten ein. Die
Stellen der Arbeit, die dem Wortlaut oder dem Sinn nach anderen Werken entnommen wurden, sind unter Angabe der Quellen der Entlehnung kenntlich gemacht. Die
Arbeit ist noch nicht veröffentlicht oder in gleicher oder anderer Form an irgendeiner
Stelle als Prüfungsleistung vorgelegt worden.
Ort, Datum
Reinhard Heinke