Rutherford (1920) and Chadwick (1932)

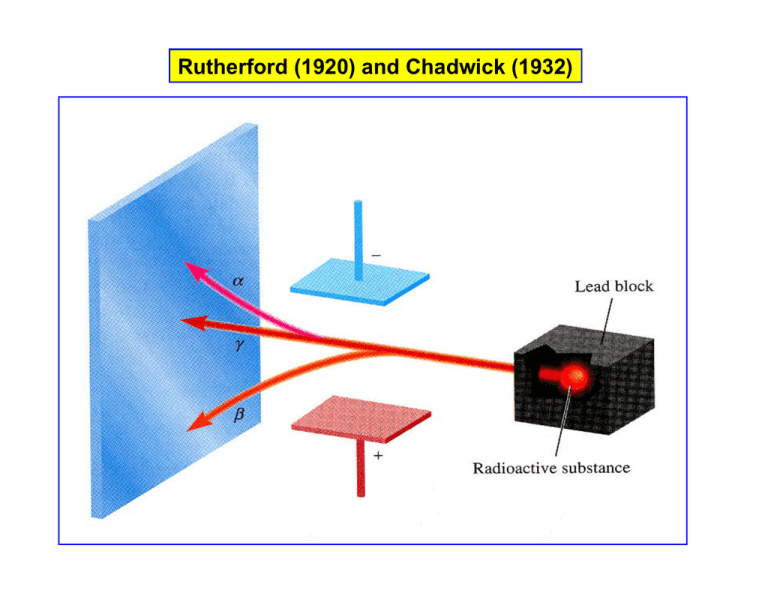
Rutherford (1920) and Chadwick (1932)
N = N0 e-kt
 ln N = ln N0 - kt
 k = 0,693/t1/2
Die elektronische Struktur der Atome
• Einheiten, Atomstruktur (subatomare Teilchen)
• Isotope & Radioaktivität
• Die Wellennatur des Lichts
• Gequantelte Energien und Photonen
• Linienspektren & das Bohr’sche Atommodell
• Das wellenartige Verhalten von Materie
• Quantenmechanik & Atomorbitale
• Darstellung von Orbitalen
• Mehr-Elektronen-Atome
• Elektronenkonfigurationen
…und das Periodensystem der Elemente
Atom: 200-500 pm
Atomkern: 0,01 pm
Elektronische Struktur
Kenntnisse aus Spektroskopie
Energie ist gequantelt!


„Welle“
Planck (ca. 1900)
Wellenlänge:
 (cm)
Wellenzahl: 1/ (cm-1)
Frequenz:
 = c/ = s-1
c = 3 x 1010 cm s-1 = 3 x 108 m s-1
Energie:
E = h = hc/ = J
h = Planck Konstante = 6,626 x 10-34 J s
Elektromagnetische Strahlung
Spektroskopische Vorgänge
E2
E
1
2
E1
1 Energie Aufnahme: Absorption
E = E2 – E1 = h
2 Energie Abgabe: Emission
E = E1 – E2 = -h
Ein kontinuierliches Spektrum
Spektroskopische Vorgänge
E2
E
1
2
E1
1 Energie Aufnahme: Absorption
E = E2 – E1 = h
2 Energie Abgabe: Emission
E = E1 – E2 = -h
Ein Emissions-Linienpektrum
Verschiedene Emissions-Linienspektren
Emissionsspektren der Edelgase
Verschiedene Emissions-Linienspektren
Das Wasserstoffspektrum
Johann Jacob Balmer
(Physicist, 1825 – 1899)
Das Bohr-Atommodell
1. Das Elektron kann sich nur auf bestimmten Kreisbahnen aufhalten, die konzentrisch
um den Atomkern angeordnet sind. Die Bahnen werden mit Buchstaben (K, L, M, N,.....)
oder Zahlen (n = 1, 2, 3, 4,......) bezeichnet.
2. Für jede Bahn, hat das Elektron eine bestimmte Energie. Die Energie nimmt zu mit
Zunahme in „n“
3. Ein Elektron auf der innersten Bahn (Atom im Grundzustand) kann Energie
aufnehmen und auf eine größere Bahn springen und einen höheren Energiezustand
annehmen (Atom im angeregten Zustand)
4. Wenn das Elektron von einem angeregten Zustand auf einen innen liegenden Bahn
springt, wird ein definierter Energiebetrag frei gesetzt und als Lichtquant emittiert.
Das Wasserstoffspektrum
Das Wasserstoffspektrum
E
Das Bohr-Atommodell
Alle bewegten Teilchen besitzen Welleneigenschaften
(de Broglie, 1920)
Louis de Broglie
(1892-1987)
Die Schrödinger Gleichung (1926)
…beschreibt die Welleneigenschaften
eines Elektrons durch Position, Masse,
Gesamtenergie und Potentielle Energie
Erwin Schrödinger
(1887-1961)
Die Heisenberg-Unschärferelation
Es ist grundsätzlich unmöglich von einem
Objekt den genauen Aufenthaltsort (x) und
den Impuls (mv) zu bestimmen
(x).(mv)  h/4
Werner Heisenberg
(1901-1976)
Dualistische Natur des Elektrons
Elektron als „Teilchen“ oder „Welle“
Teilchen:
Einstein
(für Photonen)
Welle:
De Broglie
E = mc2
(J)
(kg.m2.s-2)
E = h = hc/ (J)
mc2 = hc/
 = h/mc
 = h/mv
(v = Geschwindigkeit eines Elektrons)
Schrödinger Gleichung
De Broglie (1924): Elektron als Welle
( = h/mv)
Schrödinger (1926): Wellenmechanik
Elektron = Energiewelle
= Wolke negativer Ladung
„Orbital“
Wellenmechanik:  (Amplitude)
Wahrscheinlichkeit: 2
Wahrscheinlichkeitsdichte
Aufenthaltwahrscheinlichkeit
n = sin(.n.x/d)
n = 1, 2, 3, ....
d = Länge der Saite
n./2 = d
(bei n = 2 ist d = )
Anzahl Knotenpunkte
=n-1
 = Amplitude
2 = Intensität
= „Ladungsdichte“
R(r): Radiale Funktion “R”: Elektronendichte an
verschiedenen Abständen vom Kern
Radiale Wahrscheinlichkeitsfunktion 4πr2R2 beschreibt die
Wahrscheinlichkeit das Elektron in einem best. Abstand
vom Kern, summiert über alle Winkel, zu finden.
Quantenzahlen
Verschiedene Emissions-Linienspektren
Die elektronische Struktur der Atome
• Einheiten, Atomstruktur (subatomare Teilchen)
• Isotope & Radioaktivität
• Die Wellennatur des Lichts
• Gequantelte Energien und Photonen
• Linienspektren & das Bohr’sche Atommodell
• Das wellenartige Verhalten von Materie
• Quantenmechanik & Atomorbitale
• Darstellung von Orbitalen
• Mehr-Elektronen-Atome
• Elektronenkonfigurationen
…und das Periodensystem der Elemente
px, py, pz
dx2-y2, dz2,
dxy, dxz, dyz
n = 1, 2, 3, 4, ......
l = 0, 1, 2, ......... (n-1)
m = 0, 1, 2, ....... l
Anzahl = 2l + 1
n = 1, l = 0, m = 0
n = 1, l = 0, m = 0
n = 2, l = 0, m = 0
R(r): Radiale Funktion “R”: Elektronendichte an
verschiedenen Abständen vom Kern
Radiale Wahrscheinlichkeitsfunktion 4πr2R2 beschreibt die
Wahrscheinlichkeit das Elektron in einem best. Abstand
vom Kern, summiert über alle Winkel, zu finden.
Quantenzahlen & Atomare Wellenfunktionen
Y(,): Die Winkel-abhängige Funktion Y
Beschreibt die Form des Orbitals sowie die
Orientierung im Raum: Y(,)  s, p, d Orbital
Abhängig von l und m
Wie ändert sich die Aufenthaltswahrscheinlichkeit von
Punkt zu Punkt (im Raum) bei konst. Kernabstand?
Quantenzahlen & Atomare Wellenfunktionen
Quantenzahlen & Atomare Wellenfunktionen
n = 2, l = 1, m = -1, 0, +1
Quantenzahlen & Atomare Wellenfunktionen
Die s- und drei p-Orbitale:
Elektronendichte
auf den Achsen!
n = 3, l = 2, m = -2, -1, 0, +1, +2
Elektronendichte
auf den Achsen!
dx2–y2 & dz2
Elektronendichte zwischen den Achsen in den entsprechenden Ebenen!
dxy
dxz
dyz
n = 4, l = 3, m = -3, -2, -1, 0, +1, +2, +3