Übungen zu Ersatzwiderständen

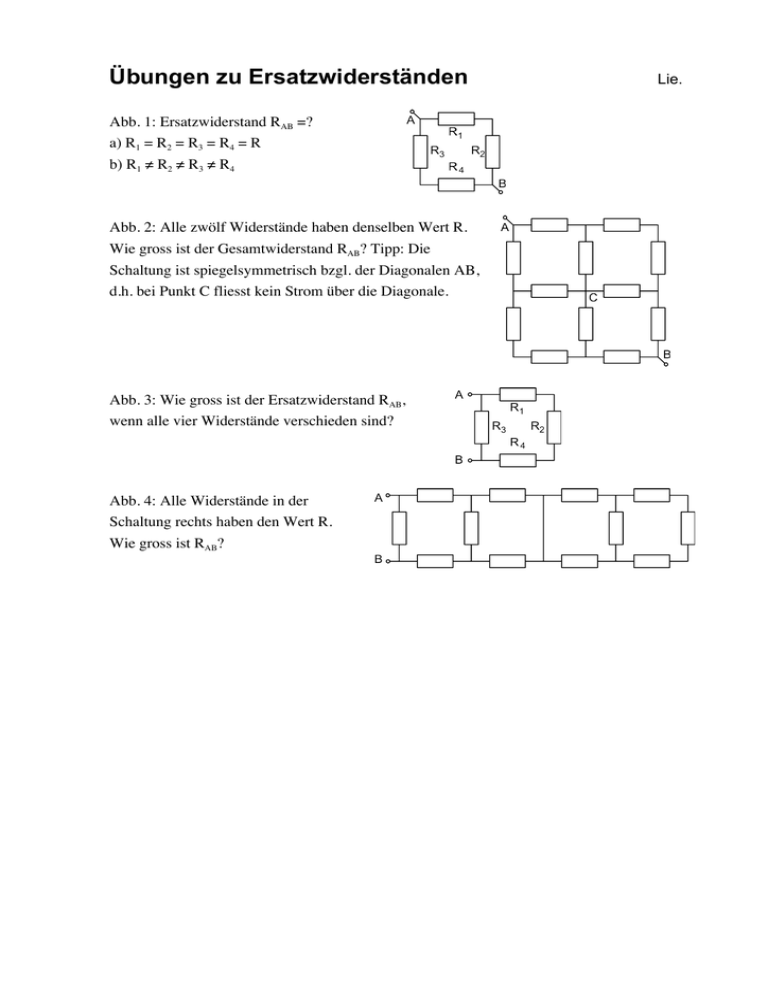
Übungen zu Ersatzwiderständen
Abb. 1: Ersatzwiderstand RAB =?
a) R1 = R2 = R3 = R4 = R
b) R1 ≠ R2 ≠ R3 ≠ R4
Abb. 2: Alle zwölf Widerstände haben denselben Wert R.
Wie gross ist der Gesamtwiderstand RAB? Tipp: Die
Schaltung ist spiegelsymmetrisch bzgl. der Diagonalen AB,
d.h. bei Punkt C fliesst kein Strom über die Diagonale.
Abb. 3: Wie gross ist der Ersatzwiderstand RAB,
wenn alle vier Widerstände verschieden sind?
Abb. 4: Alle Widerstände in der
Schaltung rechts haben den Wert R.
Wie gross ist RAB?
Lie.
Lösungen zu Übungen mit Ersatzwiderständen
1a) RAB = R b) RAB
€
€
−1
⎛ 1
1 ⎞
= ⎜
+
⎟
⎝ R1 + R2 R3 + R4 ⎠
2) Man kann die Schaltung entlang der Diagonalen teilen. Die linke untere und die
rechte obere
Ecke sind dann parallel geschaltet, d.h. RAB = 12 ( R + R + R) = 32 R
€
3) RAB
€
Lie.
⎛ 1
⎞ −1
1
= ⎜ +
⎟
⎝ R3 R1 + R2 + R4 ⎠
€
4) Die ganze rechte Hälfte der Schaltung ist kurzgeschlossen (fällt also weg).
−1
⎛ 1
⎞ −1 ⎛ 8
⎛ 1
⎞ −1 8
1 ⎞
1
3
2
Rhalbrechts = ⎜ +
+
⎟ = 3 R ⇒ RAB = ⎜ +
⎟ = 11 R
⎟ = ⎜
2
⎝ R R + R ⎠
⎝ 8R 3R + 2R + 3R ⎠
⎝ R R + 3 R + R ⎠