j - Uni Kassel
Werbung
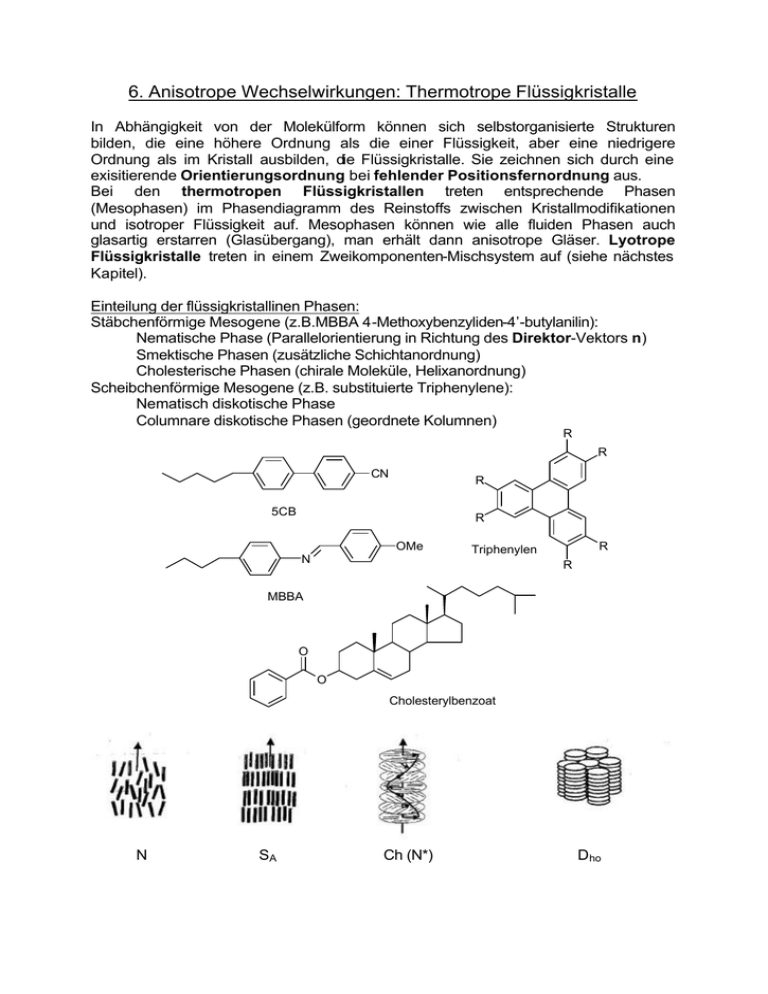
6. Anisotrope Wechselwirkungen: Thermotrope Flüssigkristalle
In Abhängigkeit von der Molekülform können sich selbstorganisierte Strukturen
bilden, die eine höhere Ordnung als die einer Flüssigkeit, aber eine niedrigere
Ordnung als im Kristall ausbilden, die Flüssigkristalle. Sie zeichnen sich durch eine
exisitierende Orientierungsordnung bei fehlender Positionsfernordnung aus.
Bei den thermotropen Flüssigkristallen treten entsprechende Phasen
(Mesophasen) im Phasendiagramm des Reinstoffs zwischen Kristallmodifikationen
und isotroper Flüssigkeit auf. Mesophasen können wie alle fluiden Phasen auch
glasartig erstarren (Glasübergang), man erhält dann anisotrope Gläser. Lyotrope
Flüssigkristalle treten in einem Zweikomponenten-Mischsystem auf (siehe nächstes
Kapitel).
Einteilung der flüssigkristallinen Phasen:
Stäbchenförmige Mesogene (z.B.MBBA 4-Methoxybenzyliden-4’-butylanilin):
Nematische Phase (Parallelorientierung in Richtung des Direktor-Vektors n)
Smektische Phasen (zusätzliche Schichtanordnung)
Cholesterische Phasen (chirale Moleküle, Helixanordnung)
Scheibchenförmige Mesogene (z.B. substituierte Triphenylene):
Nematisch diskotische Phase
Columnare diskotische Phasen (geordnete Kolumnen)
R
R
CN
R
5CB
R
OMe
N
R
Triphenylen
R
MBBA
O
O
Cholesterylbenzoat
N
SA
Ch (N*)
Dho
Maier-Saupe-Theorie der nematischen Phase
Die nematische Phase hat eine höhere Ordnung als die isotrope Flüssigkeit. Man
kann sie daher durch einen Ordnungsparameter definieren. Da die Richtungen n
und –n ununterscheidbar sind, kommt erst das Quadrat des Richtungskosinus der
Molekülorientierungen in Frage,
S=
1
3cos 2 θ − 1
2
In der isotropen Phase ist S = 0, bei vollständiger Orientierung wird S = 1.
Die Maier-Saupe-Theorie ist eine mean-field-Theorie, d.h. sie beschreibt die
Orientierungsenergie eines Dipols im Feld der anderen
ui = −
A 1
S ( 3cos θ i −1)
V2 2
(A Wechselwirkungsparameter, V spezifisches Volumen)
Die Boltzmann-Statistik ergibt Innere Energie und Ordnungsparameter durch
selbstkonsistente Lösungen
1
ui
u exp −
d cos θ
N∫
kT
i
U=
i
0
2
1
ui
∫ exp − kT d cos θ
i
0
Am Phasenübergang nematisch-isotrop (Klärpunkt) sinkt S sprunghaft von 0.43 auf 0.
Die freie Enthalpie G(S) hat hier zwei Minima. Die Beschreibung kann auf statistischthermodynamischem Wege über die Zustandssumme erfolgen oder durch eine
direkte Reihenentwicklung
1
1
1
G = G0 + aS 2 + bS 3 + cS 4 + ...
2
3
4
(Landau-de Gennes).
Krümmungselastizität
Die Eigenschaften der Flüssigkristalle ist wesentlich durch ihr elastisches Verhalten
bestimmt. Es gibt drei Grundtypen der Verbiegung des Direktorfeldes mit jeweils
einer zugehörigen elastischen Konstanten:
•
Spreizung (splay)
F=
1
r 2
K11 ( div n )
2
•
Verdrillung (twist)
F=
1
r
r 2
K 22 ( n ⋅ rot n )
2
•
Biegung (bend)
F=
1
r
r 2
K33 ( n × rot n )
2
Alle elastischen Konstanten sind klein (0.1 J/m3) und von ähnlicher Größe, so daß oft
eine Einkonstanten-Näherung verwendet werden kann.
Die krümmungselastischen Eigenschaften sind auch verantwortlich für das Ausbilden
von Domänengrenzen (boundaries), die im Polarisationsmikroskop charakteristische
Texturen ergeben.
Elektrooptische Effekte und Displayanwendungen
Flüssigkristalle sind optisch und elektrisch anisotrop, z.B. bei Nematen (uniaxiale
Orientierung) gilt für die Komponenten des Dielektrizitätstensors
ε P > ε⊥
Bei Anlegen eines äußeren elektrischen Feldes ist die Energie
1 r r
1
W = − E ⋅ D = − (ε ⊥ E12 + ε ⊥E 22 + ε PE23 )
2
2
(im Koordinatensystem des Moleküls). Dies ist energetisch am günstigsten für ein
Feld in Richtung der Moleküllängsachse E = { 0,0, E3 } . Flüssigkristalle orientieren sich
also im elektrischen Feld. Achtung: Dies ist keine Dipolorientierung, da beide
Feldpolungen die gleiche Orientierung ergeben. Im Gegenteil, oft koppeln sich
Mesogene mit permanentem Dipolmoment antiparallel.
Eine wichtige Anwendung sind Flüssigkristalldisplays. In der Schadt-Helfrich-Zelle
(Twisted Nematic-Zelle) befindet sich der Flüssigkristall zwischen zwei Indium-ZinnOxid-(ITO-)beschichteten Substraten, die durch Beschichtung z.B. mit Polyimid und
Reiben eine Vorzugsrichtung vorgeben. Durch Verdrehen der Orientierungsschichten
um 90° wird eine Verdrillung vorgegeben. Durch zwei gekreuzte Polarisatoren
erscheint die Zelle hell, da die Polarisationsebene des Lichtes durch die
Helixanordnung gedreht wird. Wird jetzt eine Spannung angelegt, so orientieren sich
die Moleküle senkrecht zu den Elektrodenflächen (homöotrop). Das Display erscheint
jetzt optisch isotrop und es wird kein Licht mehr durchgelassen.
Die Einschaltzeit hängt von den elastischen Konstanten und der angelegten
Spannung ab, die Ausschaltzeit nur von den elastischen Konstanten.
7. Amphiphile Moleküle, lyotrope Mesophasen
Eine wichtige Gruppe, die lyotrope Mesophasen ausbildet, sind die amphiphilen
Moleküle (Tenside, Detergentien). Sie bestehen aus einer hydrophilen Kopfgruppe
und einer hydrophoben Schwanzgruppe (z.B. SDS, Natriumdodecylsulfat). An
Grenzflächen bilden sie geordnete Adsorptionschichten und in Volumenphasen
können sie zu Kolloiden (Mizellen) aggregieren.
O
S
SDS
O
Na+
O
Monomolekulare Grenzflächenschichten
An der Oberfläche einer wäßrigen Tensidlösung (gegenüber Gas oder einem
Festkörper) ordnen sich die amphiphilen Moleküle so, daß ihr hydrophiler Kopf ins
Wasser zeigt, während die hydrophoben Alkylketten dem zweiten Medium
zugerichtet sind. Die Belegung von Gas-Flüssig-Grenzflächen kann mit einer
Langmuir-Waage gemessen werden. Dabei wird der Oberflächendruck als Differenz
der Oberflächenspannungen der Lösung und des Lösungsmittels gegen die Fläche
gemessen. Verkleinert man die Fläche, bis der Druck sprunghaft steigt, erhält man
eine Monoschicht. Diese Monoschichten lassen sich auf feste Substrate aufziehen
(Langmuir-Blodgett-Technik). Solche Schichten können Phasenübergänge wie in
Festkörpern aufweisen.
Mizellbildung
Werden ionische Tenside in Wasser gelöst und die elektrische Leitfähigkeit der
Elektolytlösung gemessen, so beobachtet man ab einer bestimmten Konzentration
ein drastisches Sinken der Leitfähigkeit (bei niedrigeren Konzentrationen gilt das
Kohlrausch-Gesetz: Die Äquivalentleitfähigkeit in Ω-1 cm-1 mol-1 nimmt linear mit √c
ab). Man hat die kritische Mizellbildungskonzentration CMC erreicht. Ab hier
ändert sich die Beweglichkeit der Ionen durch Aggregation zu Mizellen.
Die Einzelmoleküle sind im Gleichgewicht mit den Assoziaten
j A1 ƒ A j
mit einer Gleichgewichtskonstanten (Assoziationskonstante)
Aj
∆G
K j = j = exp −
,
kT
[ A1 ]
wobei µ0 jeweils für das chemische Standardpotential steht.
Gewöhnlich stehen Mizellen unterschiedlicher Größen miteinander im Gleichgewicht.
Betrachten wir jedoch nur eine Mizellengröße und beachten die Randbedingung, daß
die Gesamtanzahl der Monomere sich bei der Mizellbildung sich nicht ändert
j Aj + [ A1 ] = c ,
ergibt sich
K=
c − [ A1 ]
j [ A1 ]
j
c − [ A1 ]
⇒ [ A1 ] =
jK
1 j
Da der Zähler auch bei hohen Konzentrationen nicht größer als 1 werden kann,
ergibt sich als kritische Mizellbildungskonzentration:
CMC = ( jK )
−1/ j
Die Mizellbildungsenthalpie ergibt sich aus der Temperaturabhängigkeit der
Gleichgewichtskonstanten (nach van’t Hoff) zu
∂ ln CMC = − ∆H
∂T
nRT 2
mit 1< n ≤ 2
Die Entropieänderung ist trotz der Zusammenlagerung mehrerer Moleküle positiv, da
die Lösungsmittelmoleküle, die sonst die einzelnen Tensidmoleküle solvatisieren
müßten, mehr Freiraum bekommen.
Mizellen können kugelförmig sein, aber
auch stäbchen- oder scheibchenförmig. Entsprechend können sich die
Mizellen zu analogen Mesophasen
ordnen wie thermotrope Flüssigkristalle.
Doppelschichten
Eine besondere Bedeutung haben
Strukturen, bei denen sich großflächig
zwei Schichten zusammenlagern, so
daß die Kopfgruppen jeder Seite nach
außen zeigen und die Schwanzgruppen nach innen. Diese Doppelschichten sind der Grundbaustein von
lamellaren Mesophasen, Schäumen
(Seifenblasen) und biologischen Membranen.











