Kerne und Teilchen

Kerne und Teilchen
SS 2004
1
2
Inhaltsverzeichnis
Inhaltsverzeichnis
1 Einleitung
5
1.1
Geschichte der Kern- und Teilchenphysik . . . . . . . . . . . . . . . . .
5
1.2
Grundbegriffe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
1.2.1
Größenordnungen . . . . . . . . . . . . . . . . . . . . . . . . .
5
1.2.2
Nomenklatur der Kernphysik . . . . . . . . . . . . . . . . . . . .
6
2 Einführung in die Kernphysik
2.1
8
Kerne und ihre Eigenschaften . . . . . . . . . . . . . . . . . . . . . . . .
8
2.1.1
Elektrische Ladung . . . . . . . . . . . . . . . . . . . . . . . . .
8
2.1.2
Masse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
2.1.3
Bindungsenergie . . . . . . . . . . . . . . . . . . . . . . . . . .
9
2.1.4
Masse des Neutrons . . . . . . . . . . . . . . . . . . . . . . . .
10
Größe und Struktur der Kerne . . . . . . . . . . . . . . . . . . . . . . .
10
2.2.1
Wirkungsquerschnitt . . . . . . . . . . . . . . . . . . . . . . . .
10
2.2.2
Rutherford-Streuung . . . . . . . . . . . . . . . . . . . . . . . .
12
2.2.3
Elektronenstreuung an Kernen . . . . . . . . . . . . . . . . . . .
14
2.3
Bindungsenergie: das Tröpfchenmodell . . . . . . . . . . . . . . . . . .
18
2.4
Kernspin und magnetisches Moment . . . . . . . . . . . . . . . . . . . .
19
2.4.1
Magnetische Dipolmomente . . . . . . . . . . . . . . . . . . . .
19
2.4.2
Experimentelle Bestimmung von µI . . . . . . . . . . . . . . . .
20
2.4.3
Komposition magnetischer Momente . . . . . . . . . . . . . . .
21
2.4.4
Höhere Momente . . . . . . . . . . . . . . . . . . . . . . . . . .
23
2.4.5
Parität und Isospin . . . . . . . . . . . . . . . . . . . . . . . . .
24
Das Schalenmodell . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
25
2.5.1
26
2.2
2.5
Potentiale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Inhaltsverzeichnis
3 Kernumwandlung
3.1
3.2
3.3
3.4
3.5
3.6
3
29
Radioaktivität . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
29
3.1.1
Zerfallsgesetze . . . . . . . . . . . . . . . . . . . . . . . . . . .
29
3.1.2
α-Zerfall . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
30
3.1.3
β-Zerfall . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
32
3.1.4
γ-Zerfall . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
38
3.1.5
Anwendung der Radioaktivität . . . . . . . . . . . . . . . . . . .
41
Kernspaltung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
3.2.1
Voraussetzungen für spontane Spaltung . . . . . . . . . . . . . .
41
3.2.2
Uranspaltung . . . . . . . . . . . . . . . . . . . . . . . . . . . .
43
Kernkraftwerke . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
43
3.3.1
Energiebilanz bei der Spaltung von 235 U . . . . . . . . . . . . . .
43
3.3.2
Betrieb durch Kettenreaktion . . . . . . . . . . . . . . . . . . . .
43
Kernfusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
44
3.4.1
Energiegewinnung . . . . . . . . . . . . . . . . . . . . . . . . .
44
3.4.2
Reaktortypen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
45
3.4.3
Energiegewinnung in Sternen . . . . . . . . . . . . . . . . . . .
46
Wechselwirkung von Strahlung mit Materie . . . . . . . . . . . . . . . .
47
3.5.1
Energieverlust für geladene Teilchen . . . . . . . . . . . . . . . .
48
3.5.2
Coulomb-Streuung . . . . . . . . . . . . . . . . . . . . . . . . .
51
3.5.3
Cerenkov-Effekt . . . . . . . . . . . . . . . . . . . . . . . . . .
51
3.5.4
Wechselwirkung von Photonen . . . . . . . . . . . . . . . . . . .
52
3.5.5
Hadronische Wechselwirkung in Materie . . . . . . . . . . . . .
53
Strahlenwirkung, Dosimetrie . . . . . . . . . . . . . . . . . . . . . . . .
54
4
Inhaltsverzeichnis
4 Detektoren und Beschleuniger
4.1
56
Detektoren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
56
4.1.1
Ionisationsdetektoren . . . . . . . . . . . . . . . . . . . . . . . .
56
4.1.2
Gasdetektoren . . . . . . . . . . . . . . . . . . . . . . . . . . .
57
4.1.3
Halbleiterdetektoren . . . . . . . . . . . . . . . . . . . . . . . .
60
4.1.4
Szintillationsdetektoren . . . . . . . . . . . . . . . . . . . . . .
60
4.1.5
Kalorimetrie . . . . . . . . . . . . . . . . . . . . . . . . . . . .
62
4.1.6
Ältere Technologien . . . . . . . . . . . . . . . . . . . . . . . .
63
4.2
Experimente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
63
4.3
Beschleuniger . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
64
4.3.1
Fixed-Target . . . . . . . . . . . . . . . . . . . . . . . . . . . .
65
4.3.2
Collider . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
65
5 Elementarteilchenphysik
5.1
5.2
5.3
67
Grundlagen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
67
5.1.1
Der Teilchenzoo . . . . . . . . . . . . . . . . . . . . . . . . . .
67
5.1.2
Fundamentale Teilchen des Standardmodells . . . . . . . . . . .
69
5.1.3
Zusammengesetzte Objekte . . . . . . . . . . . . . . . . . . . .
69
5.1.4
Fundamentale Wechselwirkung . . . . . . . . . . . . . . . . . .
73
5.1.5
Farbe und Gluonen . . . . . . . . . . . . . . . . . . . . . . . . .
75
5.1.6
Symmetrien und Erhaltungssätze . . . . . . . . . . . . . . . . . .
77
Moderne Teilchenphysik . . . . . . . . . . . . . . . . . . . . . . . . . .
81
5.2.1
Struktur der Hadronen . . . . . . . . . . . . . . . . . . . . . . .
81
5.2.2
Phänomene der schwachen Wechselwirkung . . . . . . . . . . .
83
5.2.3
Elektroschwache Vereinigung . . . . . . . . . . . . . . . . . . .
87
5.2.4
Offene Fragen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
90
Astrophysik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
90
Literatur
91
Index
92
5
1 Einleitung
1.1 Geschichte der Kern- und Teilchenphysik
1897: Entdeckung des Elektrons durch Thomson.
1910: Streuexperimente von Rutherford, Geiger, Marsden: Atom hat einen Kern.
1938-39: Zufällige Entdeckung der Kernspaltung durch Hahn und Straßmann. Korrekte Interpretation durch Meitner und Fritsch.
1942: Erste kontrollierte Kernspaltung durch Fermi in Chicago (mit der bloßen Hand“).
”
1945: Atombomben am 6. und 9. August.
50er Jahre: Ein Teilchen nach dem anderen in Höhenstrahlungsexperimenten.
ab 1950: Entwicklung von Teilchenbeschleunigern: Kontrollierte und intensive Strahlen. Entdeckung von über 300 Elementar“teilchen.
”
ab 1965: Quarkmodell, Ordnung im Teilchenzoo. Wenige Elementarteilchen: Quarks und
Leptonen.
1970: Bestätigung des Quarksmodells durch Entdeckung von punktförmigen Partonen,
die später als Quarks identifiziert werden.
1974: November-Revolution: Entdeckung des Charm-Quarks.
1977: Entdeckung des Beauty-Quarks (auch Bottom-Quark genannt).
1983: Entdeckung von W- und Z-Bosonen.
1995: Entdeckung des Truth-Quarks (auch Top-Quark genannt).
1.2 Grundbegriffe
1.2.1 Größenordnungen
1. Längeneinheiten:
• ∅Atom ≈ 10−10 m = 1Å (Ångström).
• ∅Proton ≈ 2 · 10−15 m = 2 fm (Fermi).
• ∅Quark, Lepton, Boson . 10−19 m.
q
≈ 1, 6 · 10−35 m.
• Planck-Skala: ℓPl = G~
c2
2. Energie: 1 eV ≈ 1, 6 · 10−19 J
(kinetische Energie eines Teilchens mit Ladung e nach Durchlaufen einer Spannung
von 1 V).
6
1 Einleitung
3. Masse: 1 eV
≈ 1, 8 · 10−35 kg.
c2
B:
Masse
−
e
0, 511 MeV/c2
±
π 139, 6 MeV/c2
p 938, 3 MeV/c2
n 939, 6 MeV/c2
Z 91, 2 GeV/c2
τ 178 ± 4 GeV/c2
ν mν , 0:
mνe < 2 eV/c2
mνµ < 10 keV/c2
mντ < 1 MeV/c2
≈ 5, 34 · 10−28 kg/s.
4. Impuls: 1 eV
c2
5. Drehimpuls: 1~ ≈ 6, 6 · 10−22 MeVs = 1, 97 · 10−11 MeVcm/c.
6. Ladung: e ≈ 1, 602 · 10−19 C,
e2
4πε0 ~c
= αem ≈
1
.
137
1.2.2 Nomenklatur der Kernphysik
Kernphysik: Physik der Nukleonen n, p im Verbund: Nuklide.
Schreibe dafür:
A n+
Z XN
X: chemisches Elementsymbol,
n+ : Ionisierungszahl, falls nicht vollständig ionisiert,
A Massenzahl,
Z Ladungszahl,
N Neutronenzahl.
Die leichten Kerne bilden eine Ausnahme:
1
1 H =: p
2
1 D =: d
3
1 T3 =: t
4
2 He2 =:
Proton
Deuteron
Triton
α
Masseneinheit:
1 12
m( C6 )
12 6
≈ 1, 66 · 10−27 kg
mu = 1u :=
= 931, 5MeV/c2
1.2 Grundbegriffe
Folgende Bezeichnungen werden verwendet:
Isotope: Kerne gleicher Ladungszahl; p, d, t haben z.B. Z = 1.
Isotone: Kerne gleicher Neutronenzahl; d, 32 He1 haben z.B. N = 1.
Isobare: Kerne gleicher Massenzahl; d, 23He1 haben z.B. A = 1.
Isomere: Kerne mit gleichen Z, N auf unterschiedlichen Energieniveaus;
∗
z.B. 178 Hf → 178 Hf + γ.
13
Spiegelkerne: Kerne mit vertauschbaren N, Z; z.B. 13
6 C7 ↔ 7 N6 .
7
8
2 Einführung in die Kernphysik
2 Einführung in die Kernphysik
2.1 Kerne und ihre Eigenschaften
2.1.1 Elektrische Ladung
• Bestimmung der Ladungsverteilung im Atom durch Rutherford-Streuung:
dσ
dΩ
!
θ
zZe2
=
4πε0 4E 0
!2
·
1
(sin 2θ )4
dabei ist z die Ladung des einfallenden Teilchens, E 0 seine Energie und Z die Ladung des Streuzentrums.
• Das Moseley-Gesetz:
γK
Abbildung 1: Übergang eines Elektrons in die K-Schale
Frequenz der K-Linie der Röntgenstrahlung:
1 1
νK = Ry · (Z − s) ·
−
1 n2
!
dabei ist Ry die Rydbergkonstante und s ≈ 1 für den Übergang in die unterste
Schale (Abschirmungseffekt).
2.1.2 Masse
Massenpektrometer, Prinzip von Thomson zur Bestimmung von mq . q bekannt ⇒ m bekannt. Ablenkung im E-Feld:
qEl2
qEl2
=
y=
4E kin 2mv2
2.1 Kerne und ihre Eigenschaften
9
−
m,q
E
v
}y
+
⊗
R
⊗
l
⊗
⊗
B
Abbildung 2: Massenspektrometer von Thomson
Ablenkung im B-Feld:
mv2
⇒ p = mv = qBR
R
B2 R2 2y
p2
=q
m=
2E kin
El2
F L = qvB =
Anmerkung: Verbesserung durch fokussierdende Anordnung,
∆m
m
=
1
.
2000
Beobachtungen:
• Ladung des Kerns ist Vielfaches der Elementarladung e.
• Masse des Kerns ist ungefähr Vielfaches der Protonenmasse mp .
q
3
He
4
He
2
1
p
d
t
1
2
3
m
4
Abbildung 3: Kernmassen (in mp ) und Ladung (in e)
Neben p und e muss es also einen zusätzlichen Baustein geben: das Neutron n.
2.1.3 Bindungsenergie
Starke Kräfte, die p, n auf kleinstem Raum binden ⇒ Massendefekt:
m(Z, N) = Zmp + Nmn −
EB
c2
Dabei ist m(Z, N) die Masse des Kerns mit Z Protonen und N Neutronen. Dem Massendefekt entspricht die Bindungsenergie E B .
10
2 Einführung in die Kernphysik
2.1.4 Masse des Neutrons
Bestimme md , mp . Dann kann man mn über Photospaltung des d berechnen.
2
1D
+ γ → 10 n + 11 H
daraus folgt
mn = md − mp + 2, 226 MeV/c2 = 939, 6 MeV/c2 .
Das Neutron ist etwa 1, 3 MeV/c2 schwerer als das Proton.
γ
Deuterium
1n
0
0
1
0n
1
0
11
0
0
1
p
11
00
00p
11
Abbildung 4: Photospaltung
2.2 Größe und Struktur der Kerne
2.2.1 Wirkungsquerschnitt
Der Wirkungsquerschnitt σ ist die effektive Fläche eines Streuprozesses.
Streuzentrum
R2
R1
R=R1+R2
Abbildung 5: Wirkungsquerschnitt = effektive Fläche = π · R
2.2 Größe und Struktur der Kerne
11
NT
11 0
00
00 1
11
0
1
Φ
1
0
0
1
1
0
0
1
1 0
0
0 1
1
0
1
.
NS
.
NR
Target
Abbildung 6: Streuung am Target
Bestimmung von σ:
ṄR = ṄS
NT σ
Streufläche
= Ṅ
= ΦNT σ
A
Gesamtfläche
⇒σ=
ṄR
ΦNT
mit der Einheit [σ] = 10−24 cm2 = b (Barn).
Dabei ist ṄS die Anfangsintensität der einfallenden Teilchen, ṄR die gestreute Intensität,
Φ der Fluss der einfallenden Teilchen, NT die Anzahl der Streuzentren im Target.
B:
σpp = 40mb (bei 10 GeV)
σνp = 70fb = 7 · 10−38 cm2
(bei 10 GeV)
Speziell gilt:
σtotal = σinelastisch + σelastisch
Der differentielle Wirkungsquerschnitt ist
z.B. X = E, θ, Ω....
dσ
,
dX
wobei X eine physikalische Größe darstellt,
dΩ
Φ
θ
β
Target
Abbildung 7: Winkel und Raumwinkel bei der Streuung
12
Es ist
2 Einführung in die Kernphysik
dσ
dΩ
=
dṄR 1
.
dΩ NT Φ
Es gilt auch:
dσ
dθ =
dθ
Z
2π
β=0
dσ
dΩ =
dΩ
und damit
Z
2π
0
dσ
dσ
sin θdθdβ =
2π sin θdθ
dΩ
dΩ
dσ
dσ
= 2π sin θ
dθ
dΩ
2.2.2 Rutherford-Streuung
Rutherford entwarf 1911 ein Experiment zur Strukturanalyse des Atomkerns. Dabei wurden α-Teilchen auf eine Goldfolie geschossen und die Streuwinkel der Teilchen gemessen.
1
0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
α
Detektor
1
0
0
1
0
1
0
1
0
1
0
1
θ
Goldfolie
Blende
Abbildung 8: Rutherfords Streuexperiment;
dṄR
dΩ
= Anzahl der Blitze“
”
Beobachtung:
.
N
θ
120°
Abbildung 9: Winkelabhängigkeit von Ṅ
Interpretation: Elastische Streuung der α-Teilchen am Coulomb-Potential.
Sei b der Stoßparameter:
Φ2πbdb = Φ2π sin θdθ
dσ
dΩ
2.2 Größe und Struktur der Kerne
13
dθ
111 θ
000
000
111
000
111
000
111
b
Φ
db
Abbildung 10: Streuung am Coulomb-Potential
⇒ allgemein für elastische Streuung (ohne Polarisation):
Speziell für die Coulomb-Streuung:
dσ
b db =
dΩ sin θ dθ v
E0
v0
r
111
000
θ
000
111
000
111
000b’
111
b
Abbildung 11: Coulomb-Streuung
1 2
zZe2
Energieerhaltung: mv +
= E 0 = const.
2
4πε0 r2
Drehimpulserhaltung: L = mv0 b = mvb′ = const.
⇒b=
zZe2 1
cot θ
4πε0 E 0 2
Ergebnis:
zZe2
dσ
=
dΩ
4πε0 4E 0
!2
·
1
(sin 2θ )4
Analyse von Rutherford: Größte Annäherung an den Kern wenn
E 0 = 4, 78 MeV =
zZ
· 1, 44 fm MeV ⇒ rmin = 47 fm > rAu
rmin
(rAu ist der Radius des Goldkerns).
14
2 Einführung in die Kernphysik
Bei größeren Energien ergeben sich Abweichungen wegen der Kernwechselwirkung.
Aus den Abweichungen vom elastischen Wirkungsquerschnitt erhält man die Ausdehnung
des Kerns. Einige Folgerungen:
1. Es gilt folgende Näherungsformel für den Kernradius:
1
RKern ≈ r0 · A 3
mit r0 = 1, 2 fm ( dichte Kugelpackung“).
”
B:
Kern Kernradius RKern
1
1, 03 fm
1H
2
D
2, 8 fm
1
16
2, 75 fm
8 O
197
6, 87 fm
79 Au
1
Näherung RKern · A− 3
1, 0 fm
2, 2 fm
1, 4 fm
1, 18 fm
2. Dichte der Kernmaterie:
̺Kern =
A · 1, 66 · 10−27 kg A · 1, 66 · 10−27 kg
g
= 1, 44 · 1015 3
=
4
3
VKern
cm
πRKern
3
Welchen Radius hätte die Sonne, wenn sie ganz aus Kernmaterie bestehen würde?
M⊙ = 2 · 1030 kg
M⊙
4 D 3
=
= 1, 4 · 1018 cm3
V= π
3 2
̺Kern
⇒ D = 17 km (Neutronenstern)
3. Vergleich von Kernkraft und Gravitationskraft:
Gravitationspotential:
"
#
m1 m2
−37 A1 A2 MeV
VG = G ·
= 1, 1 · 10
r
r
fm
3
m
(mit G = 6, 67 · 10−11 kgs
2 ).
Kernpotential:
VK ≈ E B ≈ 8 MeV/Teilchen ⇒
2.2.3 Elektronenstreuung an Kernen
Prinzip analog zur Rutherford-Streuung. Beachte:
E BG
E BK
= 10−38
2.2 Größe und Struktur der Kerne
15
1. E e ist definiert durch die de Broglie-Wellenlänge des Elektrons:
λ/2π < RK
(= O(fm))
mit λ/2π = p~e = 197 MeVfm/pe c2 .
Daraus folgt: pe > 200 MeV/c und E > 200 MeV.
2. Berücksichtige den Spin:
Mott-Streuung:
dσ
dΩ
!
Mott
dσ
=
dΩ
!
Rutherford
· 1 − β2(sin θ/2)2 → 0 für β → 1, θ → 180◦
Helizität = 1
Helizität = 1
Spin
11
00
00
11
00
11
Spin
e−
Kern
Helizität = −1
"linksdrehend"
Spin
e−
111
000
000
111
000
111
! verboten !
Kern
Helizität = 1
"rechtsdrehend"
Spin
Abbildung 12: Mott-Streuung; die Helizität muss erhalten bleiben
Das Elektron habe den Spin s und den Impuls p. Die Helizität
h=
p· s
= ±1
| p · s|
16
2 Einführung in die Kernphysik
muss bei der Streuung erhalten bleiben (Quantenmechanik).
Die Formel für die Streuung muss korrigiert werden, falls das Target Spin besitzt:
Dirac-Streuung:
dσ
dΩ
!
Dirac
dσ
=
dΩ
!
q2
· (cos θ/2) +
· (sin θ/2)2
2
2M
Rutherford
2
!
dabei ist M die Kernmasse, q2 ist der (quadratische) Impulsübertrag, der Term
(sin θ/2)2 beschreibt die Spin-Spin-Wechselwirkung.
3. Innere Strukturen und der Formfaktor:
Beschreibung durch Impulsübertrag
p
p
~
p
θ
1
0
0
1
q = p −~p
~
p
Abbildung 13: Impulsübertrag q
Mit q = p − p̃ ist sin θ/2 =
Mit E =
p
2m
1 |q|
2 | p|
=
q
.
2mv
gilt (nichtrelativistisch) für die Rutherford-Streuung:
dσ
dΩ
!
q
2zZe2 m
=
4πε0
!2
1
q4
Streuverhalten in Ladungsverteilung:
dσ
dσ
=
dΩ
dΩ
!
punktförmig
2
· F(q2 )
F(q2 ) ≤ 1 ist der Formfaktor.
Es gilt
2
F(q ) =
Z
i
̺(r) · e ~ q·r d3 r
Dies ist die Fourier-Transformierte der Ladungsverteilung.
Herleitung:
Es ist Ψ(r, t) = Ψ0 ei( k̃·r−ωt) . Von dQ = ̺(r)dV geht eine Sekundärwelle aus:
a
a
A(R) = Ψ(r) eik·r̃ = Ψ0 ei k̃·r eik·r̃
r̃
r̃
q2
2M 2
·
2.2 Größe und Struktur der Kerne
17
neue Welle
k
1111
0000
0000
1111
0000
1111
0000
1111
r
0000
1111
dQ
~
k
~
r
ebene Welle Ψ
r
ρ( ~r)
Abbildung 14: Streuung an einer Ladungsverteilung
mit r̃ = R − r:
1 i( k̃·r+k·r̃) 1 i( k̃·r̃+k·R−k·r) 1 i(kR) i( k̃−k)·r
e
= e
≈ e e
,
r̃
r̃
R
denn |k| = | k̃| und |r̃| ≈ |R|, kkR für große Abstände.
Integration über alle dQ liefert:
Z
Z
a
a
i(kR) i∆k·r ̺(r) 3
i(kR)
Atot (R) =
̺(r)ei∆k d3 r
Ψ0 e e
d r=
Ψ0 e
R
Q
RZe
und mit
|q| = ~|∆k|,
folgt
dσ
dσ
=
dΩ
dΩ
a=
zZe2
,
4πε0 q2
dσ
∼ |Atot |2
dΩ
!
2
Z
i
q·r 3 ~
· ̺(r)e d r .
punktförmig |
{z
}
=:|F(q2 )|2
B:
Ladungsverteilung ̺(r)
1
Punkt: 4π
δ(r)Q
a
exponentiell: 8π
e−αr
2 23 a2 r2
a
Gauß: 2π
e− 2
(
c, r ≤ R
harte Kugel:
0, r > R
|F(q2 )|
1
1+q2 q2 π2
q2
e− 2a2 ~2
3α−3 (sin α − α cos α),
mit α =
|q|
R,
~
αmin = 4, 5
R
18
2 Einführung in die Kernphysik
Aus den Streuversuchen erfahren wir über die Struktur der Kerne:
• Kerne besitzen konstante Ladungsverteilung und -dichte bis zu einem diffusen Rand.
• Die Fermi-Verteilung bestimme die Ladungsverteilung im Kern:
̺(r) =
1+
̺0
−(r−R
1/2 )/a
e
1
mit a = 0, 55 fm, R1/2 = 1, 1 A 3 fm ist ̺ ≈ 0, 17
Nukleonen
.
fm2
• Kerne können von der Kugelform abweichen (Oblaten, Zigarren...).
• Kernkräfte sind beschränkt auf den Bereich der Ladungsverteilung.
Daraus erhält man Kernmodelle.
2.3 Bindungsenergie: das Tröpfchenmodell
Bethe, Weizsäcker 1935.
Modell: Kern als inkompressible Flüssigkeit, Nukleonen als Tröpfchen.
E B = Zmp + Nmn − mKern
(setze c2 = 1).
Beobachtung:
EB
≈ const. = 8...9 MeV.
A
Ansatz für die Bindungsenergie: Die Weizsäckersche Massenformel:
EB =
aV A
Volumenterm
−
2
1
aS A 3
Oberflächenterm
− aC Z 2 A− 3 − aA
Coulombterm
1
(N − Z)2
+ δA− 2
Paarungsterm
A
Asymmetrieterm
Dabei gilt:
Volumen ∼ A
2
Oberfläche ∼ A 3
Z 2 e2
R
√
Asymmetrie: Anzahl der Zustände N ∼ E


+11, 3 MeV :
(g,g)



0
: (u,g) oder (g,u) ,
δ=


−11, 3 MeV :
(u,u)
EC ∼
2.4 Kernspin und magnetisches Moment
19
dabei bedeutet u bzw. g ungerade bzw. gerade Parität von (Protonenzahl, Neutronenzahl).
Empirische Parameter:
aV
aC
aS
aA
= 15, 5 MeV
= 0, 7 MeV
= 16, 8 MeV
= 23 MeV
Anwendung: Spaltung von Uran.
239
n + 238
92 U → 92 U → X + Y
m(U)
.
2
Spaltenergie:
Z A
= ∆E B
E F = m(Z, A) − 2m ,
2 2
2
2
1
Z2
= aS A 3 (1 − 2 3 ) + aC 1 (1 − 2− 3 )
A3
= 180 MeV
Angenommen m(X) = m(Y) =
2.4 Kernspin und magnetisches Moment
2.4.1 Magnetische Dipolmomente
1. Klassisch:
µ
00000000
A11111111
00000000
11111111
11111111
00000000
00000000
11111111
00000000
11111111
00000000
11111111
q
00000000
11111111
00000000
11111111
r
v
Abbildung 15: Klassischer magnetischer Dipol.
q 2
πr eA
T
v
πr2 eA
=q
2πr
q
=
preA
2m
µ = jA =
20
2 Einführung in die Kernphysik
also:
µ=
q
=ℓ
2m
Für Teilchen mit Spin I:
e
I
2m
klassisch gI = 1 bzw. gI < 1 für Ladungsverteilung.
µ = gI
2. Elektron:
mit µB =
e~
2me
s
µe = ge µB ,
~
−5
= 5, 8 · 10 eV/T (Bohrsches Magneton).
3. Proton:
mit µK =
e~
2mp
4. Kern:
mit gI =
s
µ p = gp µ K ,
~
−8
= 3, 2 · 10 eV/T (Kernmagneton).
I
µ I = gI µK ,
~
|µI |~
.
µK |I|
2.4.2 Experimentelle Bestimmung von µI
1. Hyperfeinstruktur-Aufspaltung (HFS) atomarer Spektren.
VHFS = −µI · B J = −|µI |B J cos(I, J),
dabei ist B J das magnetische Feld der Hülle am Kern.
√
√
und daraus
Mit F = I + J, F 2 = I 2 + J 2 + 2IJ folgt cos(I, J) = F(F+1)−I(I+1)−J(J+1)
2 I(I+1) J(J+1)
!
F(F + 1) − I(I + 1) − J(J + 1)
E HFS = a ·
,
√
√
2 I(I + 1) J(J + 1)
2
a = µ B ge µ K g I
3
B: Die 1s-Aufspaltung im H-Atom.
( a
+4, F = 1
E HFS =
− 3a4 , F = 0
und ∆E HFS = a (entspricht λ = 21cm; die interstellare H-Linie).
2. Magnetische Kernresonanz (NMR).
Prinzip: Einstrahlung von Energie auf Probe im Magnetfeld. Im statischen H0 : Ausrichtung des Spins:
( 1
+2
ms =
− 12
2.4 Kernspin und magnetisches Moment
21
111111
000000
000000
111111
000000H 0
111111
~
111111
000000
000000
111111
000000
111111
H(t)
Abbildung 16: Magnetische Kernresonanz
und ∆E(∆m − 1) = −gI µK H0 .
Mit Einstrahlung von Energie durch H(t): Absorption, resonanzartiges Umklappen
des Spins für
g I µ K H0
νH (t) =
.
h
Also: Frequenz messen ⇒ gI µK .
B: Protonen, H0 = 1T, ν = 42, 5MHz.
2.4.3 Komposition magnetischer Momente
Beobachtung:
• A gerade ⇒ I = 0, 1, 2....
• A ungerade ⇒ I = 12 , 32 , ....
• Z, N jeweils gerade ⇒ I = 0.
Ansatz:
I=
mit Ini = ℓni + sni , Ipi = ℓpi + spi .
µI =
mit µI,ni =
µK
~
X
X
gℓ ℓni + g s sni und µI,pi =
µK
~
Ini +
X
Ipi
µI,ni +
X
µI,pi
gℓ ℓpi + g s spi .
B: Vorhergesagte und experimentell gemessen Werte.
• 21 H:
1 1
+ = 1,
2 2
µI = µp + µn = (2, 79 − 1, 91)µK = 0, 88µK ,
I = Ip + In =
Iexp = 1,
µexp = 0, 86µK .
22
2 Einführung in die Kernphysik
• 31 H:
1
Iexp = ,
2
µexp = 2, 97µK .
1
In = ,
2
µI = (2, 79 + 0)µK ,
I = Ip +
X
• 42 He:
I = 0 + 0,
µI = 0 = µexp .
Iexp = 0,
Für Spin+Bahndrehimpuls gilt:
(µI · I)I
|I|2
µ=
Für I = ℓ ±
1
2
folgt:
µ = µK
g s − gℓ gℓ ±
2ℓ + 1
B:
•
17
O:
5
I= ,
2
ein Neutron ist ungepaart.
(ℓ = 2, s = 21 ).
•
17
µI = −1, 9µK
F:
5
I= ,
2
ein Proton ist ungepaart.
µI = 4, 7µK , µexp = 4, 8µK
(ℓ = 2, s = 12 ).
Schlussfolgerung: Aus I, µ erhalten wir, dass die p, n im Kern paarweise abgesättigt sind.
Verbleibendes Nukleon bestimmt (einzig und allein) I, µ, ℓ.
2.4.4 Höhere Momente
Potentielle Energie der Ladungsverteilung:
Z
W=
Φ(r)̺(r)dr.
V
2.4 Kernspin und magnetisches Moment
23
dV
11
00
00
11
E(r)
Ladungsverteilung
Abbildung 17: Ladungsverteilung im E-Feld
Ansatz:
∂E j
1X
xi x j
|0 .
Φ(r) = Φ(0) + r · ∇Φ(r)|0 +
|{z} | {z } 2
∂x
i
i, j
=:W0
=:W1
|
{z
}
=:W2
Mit
Z
Z
W0 ̺(r)dr =
Z
Φ(0)̺(r)dr = ZeΦ(0) (potentielle Energie der Gesamtladung)
Z
W1 ̺(r)dr = −E(0)
r̺(r)dr = 0
V
V
denn: ̺(r) = QΨ∗ (r)Ψ(r), Ψ(r) = ±Ψ(−r), ̺(r) = ̺(−r)
Z
Z
Z
⇒
r̺(r)dr =
r̺(−r)dr = − r̺(r)dr
Physikalische Konsequenz: Dipolmoment De = 0 (von Kernen).
Das Quadrupolmoment:
Z
Z X
∂E j
1
W2 ̺(r)dr = −
xi x j
|0 ̺(r)dr
2 V i, j
∂xi
Z X
dE
1
(3xi x j − r2 δi j ) ̺(r)dr
=−
6 V i, j
dxi
∂E j
1X
=−
|0
Qi, j
6 i, j
∂xi
dE
(beachte: δi j dx
= 0, denn ∇E|0 = 0).
i
Systeme mit Rotationsenergie bzgl. der z-Achse:
Z
Qzz = (3Z 2 e2 − r2 )̺(r)dr
V
B: Zigarre“und Oblate“:
”
”
24
2 Einführung in die Kernphysik
Zigarre
b
b
a
a
Oblate
!
a + b 2(b − a) 4
4
= ZehRi2 δ.
Qzz = Ze
5
2 | a{z
+ b} 5
| {z }
=hRi2
=hδi
δ < 0 Zigarre, δ = 0 Kugel, δ > 0 Oblate.
2.4.5 Parität und Isospin
1. Parität P: Symmetrie der Wellenfunktion unter räumlicher Spiegelung am Ursprung.
Die Parität ist eine multiplikative Quantenzahl.
PΨ(r) = PΨ(−r),
P 2 Ψ(r) = P2 Ψ(r) = Ψ(r) ⇒ P = ±1
z.B. Wellenfunktion eines Teilchens im Zentralpotential.
Ψ(r) = Rnℓ (r)Yℓm (θ, ϕ),
ℓ = 0, 2, ... für P = +1, ℓ = 1, 3, .. für P = −1. Konvention:
p, n, e− : P = +1
p, n, e+ : P = −1
B: Parität des π− :
Beobachte π− + d → n + n.
• Pion wird eingefangen, formt Atom im Grundzustand, ℓ = 0.
P(Ψ) = +1 = P(d)P(π− ) = P(n)P(p)P(π− ) = +1,
da Id = 1, ℓ = 0.
• Betrachtung des nn-Systems: Gesamtdrehimpuls I = 1 (muss erhalten bleiben).
Möglichkeiten:
snn
snn
snn
snn
= 1, ℓ = 0
= 1, ℓ = 1
= 1, ℓ = 2
= 0, ℓ = 1
2.5 Das Schalenmodell
25
Beide n sind Fermionen, also muss die Gesamtwellenfunktion antisymmetrisch sein:
snn = 1 symmetrisch, ℓ = 1 antisymmetrisch
⇒ P(nn) = P(n)P(n)P(Ψ) = (+1) · (+1) · (−1) = −1 = P(π− )
2. Isospin T : Wegen der Ladungsunabhängigkeit der Kernkräfte und da mp ≈ mn fasst
man p und n unter dem Begriff Nukleon zusammen. Beschreibe die Symmetrie der
Nukleonen durch den Isospin:
1
1
T (p) = , T 3 (p) = + ,
2
2
1
1
T (n) = , T 3 (n) = − .
2
2
Entsprechend für das Pion mπ+ = mπ− ≈ mπ0 :
T (π) = 1,
T 3 (π+ ) = +1, T 3 (π0 ) = 0, T 3 (π− ) = −1.
B:
p + p → d + π+
T:
1 1
+ =0+1
2 2
mit Wirkungsquerschnitt σ1 ,
p + n → d + π0
T : 0 oder 1 = 0 + 1
mit Wirkungsquerschnitt σ2 . Es sind treten zu 50% T (p + n) = 0 und zu 50%
T (p + n) = 1 auf. Es ist dann σ1 = 2σ2 .
2.5 Das Schalenmodell
Vorhersage der inneren Eigenschaften (wie Momente, I, E B ...).
Experimentelle Hinweise: Besondere Stabilität von Kernen mit magischen Zahlen“ N
”
oder Z = 2, 8, 14, 20, ....
2.5.1 Potentiale
Hinweis auf Form der Dichterverteilung.
Ansatz:
• Jedes Nukleon bewegt sich im Kern unabhängig im mittleren Potential.
26
2 Einführung in die Kernphysik
• Reichweite der Kernkraft ≤ R0 ≈ 1, 3 fm.
Die Bewegungsgleichung:
A
X
i=1


A 
X
X

 ~
−
△i + Vi j (ri − r j ) Ψ(r1 , r2 , ..., rA )
Hi Ψ(r1 , r2 , ..., rA ) =
2mi
j,i
i=1
= EΨ(r1 , r2 , ..., rA ),
P
Q
mit Ψ = A Ψi (ri ), Hi Ψi = E i Ψi und dem Potential Vi j .
i, j
i
Eine numerische Lösung liefert z.B. das Hartree-Fock-Verfahren. Betrachte nun einen
Näherungsansatz:
! X
X
X
X
~
△i +Vi (ri ) +
Vi j (ri − r j ) −
Vi r i ,
H =
Hi =
−
2mi
i< j
i
i
i
|
{z
}
=:VR
VR beschreibt die Restwechselwirkung und es ist VR ≈ 0. Dies entspricht einem idealen
Fermigas.
1. Harmonischer Oszillator im dreidimensionalen (Abb. 18):
!
m
r2
V(r) = −V0 1 − 2 = ω2 (r2 − R2 )
R
2
Lösung:
3
E N = ~ω(N + )V0 ,
2
mit N = (2n − 1) + ℓ und n = 1, 2, ..., ℓ = 0, 1, ....
40
Guter Ansatz für leichte Kerne, z.B. 42 He, 816 O, 20
Ca.
2. Kastenpotential (Abb. 19):
V(r) =
(
V0 , 0 ≤ r ≤ L
0,
sonst
3. Woods-Saxon-Potential (mit ℓs-Kopplung, Abb. 20):
!
V0
Ze2
V(r) = −
− cℓ · s +
1 + e(r−R0 )/a
4πε r
| {z 0 }
nur für p
In diesem Modell entsprechen die magischen Zahlen abgeschlossenen Schalen. Die
Spin-Bahn-Kopplung verursacht ein große Aufspaltung der Energieniveaus.
Zusammenfassung:
• Form des Potentials: Streuexperimente.
• Schalenmodell: magnetische Momente, Kernspin, Korrekturen zu E B .
2.5 Das Schalenmodell
27
r
EN
Summe der Zustände
3
+6+14
40
2
+2+10
20
1
+2+3
8
+2
2
N=0
Vo
11
0
0
01
1
0
Abbildung 18: Harmonischer Oszillator
r
EN
Summe der Zustände
2s
1d
1p
20
18
8
1s
2
Vo
Abbildung 19: Kastenpotential
EN
r
Vo
Abbildung 20: Woods-Saxon-Potential
28
3 Kernumwandlung
3 Kernumwandlung
Beobachtung: chemische Elemente wandeln sich um durch Aussenden von Strahlung.
α-Zerfall: (starke Wechselwirkung, Tunneleffekt)
α A−4
A
Z X → Z−2 Y
+ 42 He
β-Zerfall: (schwache Wechselwirkung)
e± A
A
→
X
Z
Z∓1 Y
±
+e +
(
νe
νe
γ-Zerfall: (elektromagnetische Wechselwirkung)
A ∗ γ A
ZX → ZX
3.1 Radioaktivität
3.1.1 Zerfallsgesetze
Zerfallswahrscheinlichkeit:
w = const.∆t =
∆N
N
(N = Teilchenzahl). Daraus ergeben sich:
N(t) = N0 e−λt
dN
= −λN(t) Aktivität,
A(t) =
dt
λ heißt Zerfallskonstante. Die Einheit von A ist Becquerel (Zerfälle pro Sekunde).
B: Aus der Umwelt:
Granit: A ≈ 1000Bq/kg
Tonschiefer: A ≈ 700Bq/kg
Gartenerde: A ≈ 400Bq/kg
Im Haus:
Radon in der Luft: A ≈ 50Bq/m3
Leitungswasser: A ≈ 30Bq/Liter
Kalium im Körper: A ≈ 4500Bq
Weitere Größen:
ln 2
Halbwertzeit
λ
1
(mittlere) Lebensdauer
τ=
λ
~
Γ = = ~λ Zerfallsbreite
τ
t1/2 =
3.1 Radioaktivität
29
3.1.2 α-Zerfall
Voraussetzung:
Q = (m(Z, A) − m(Z − 2, A − 4) − mα ) c2 > 0,
dann ist
Eα =
Q
1+
.
mα
m(Z−2,A−4)
Zuammenhang zwischen t1/2 und E α :
X
t1/2
Po 0, 3µsec
238
877a
Pu
238
U 4, 5 · 109 a
212
Eα
8, 8 MeV
5, 6 MeV
4, 3 MeV
Beobachtungen beim α-Zerfall:
Linienspektren ⇒ Zweikörperzerfall.
Zusammenhang:
ln λ = A + B log Rα = Ã + B̃ log E α
Interpretation von Gamow, London, Henry (1928):
1. Im Mutterkern bildet sich ein α-Zustand mit Wahrscheinlichkeit λα .
V
Eα
RC
α
n
r
p
Abbildung 21: Coulomb-Schwelle
Es entsteht ein gebundenes System Y +α. Spontaner Zerfall kann vorkommen, wenn
E α > VC (R0 ) mit dem Coulomb-Potential
VC (R0 ) =
und dem Kernradius R0 .
2ZY e2
4πε0 R0
30
3 Kernumwandlung
B: Zerfall von Uran:
238
92 U
Man erhält:
VC =
→ 234
90 Th + α
1, 44 MeVfm · 90 · 2
= 35 MeV ≫ E α = 4, 27 MeV
√3
1, 2 · 234 fm
2. α-Teilchen tunnelt durch die Coulomb-Schwelle:
• Eindimensional (Abb. 22):
Ψ initial
V0
Ψ final
d
Abbildung 22: Durchtunneln eines Potentials
Vergleiche |Ψin |2 mit√ |Ψout |2 (berücksichtige Stetigkeit): Die Transmission T ist
2
proportional zu e− ~ 2m|VC −Eα|d .
• Dreidimensional (Abb. 23):
V0
r
Abbildung 23: Annäherung durch Stufen
2
T ist proportional zu e− ~
R RC √
2m|VC (r) − E α |dr.
R
0
• α-Zerfall: T α = e−G . Mit dem Gamow-Faktor
r
2 2m 2ZY e2
G=
~ E α 4πε0
3. Stoßfrequenz:
vα
Stöße
≈ 1020 ...1021
2R0
sec
(R0 Kernradius, vα Geschwindigkeit des α-Teilchens).
f =
Daraus folgen die Wahrscheinlichkeit λα für das Entweichen aus dem Kern und die Halbwertzeit:
λ = λα T α f,
ln t1/2 ∼ ln
1
1
∼G∼ √ .
λ
Eα
3.1 Radioaktivität
31
3.1.3 β-Zerfall
1914 Chadwick: e+ , e−-Abstrahlung mit kontinuierlichem Spektrum.
Mysterium: Wo kommen e+ , e− her? Warum kontinuierliche Spektren?
Diskussion: Energie und Impuls nicht erhalten.
B:
212
83 Bi
α2 ↓
208
81 Ti
β1
→
β2
→
212
84 Po
↓ α1
208
82 Pb
208
2
−
E max (β) + E(α) = (m(212
83 Bi) − m(82 Pb) − mα − me )c = 11, 2 MeV.
Erwartung, falls β-Zerfall ein Zweikörperzerfall:
Für ug-Kern (I = 21 ) → gu-Kern (I = 0, 1), da e+ , e−-Spin 21 . Dies wurde aber nie beobachtet!
Also machte Pauli 1938 den Vorschlag:
Der β-Zerfall ist ein Dreiteilchenzerfall mit Neutrino ν.
Eigenschaften des ν:
A
• Z = 0, da ZA X → Z±1
Y + e∓ + ν.
• Masse sehr klein: mνe . 2eV/c2 .
Elementarer Prozess:
n → p + e− + νe + 0, 8 MeV
(falls n frei: τn ≈ 900sec). Der umgekehrte Prozess ist für freies p nicht möglich, da
mn > mp + me .
β-Zerfälle im Kern:
1. β− -Zerfall:
A
ZX
A
→ Z+1
Y + e − + νe
Energiedifferenz:
∆E = ((M(Z, A) − Zme ) − (M(Z + 1, A) − (Z + 1)me ) − me ) c2
= (M(Z, A) − M(Z + 1, A)) c2 > 0,
dabei ist M(Z, A) die Atommasse von ZA X und mν ≈ 0.
E 0 = E kin,tot = E e + E γ = ∆E − me c2 .
32
3 Kernumwandlung
2. β+ -Zerfall:
A
ZX
A
→ Z−1
Y + e + + νe
Energiedifferenz:
∆E = ((M(Z, A) − Zme ) − (M(Z − 1, A) − (Z − 1)me ) − me ) c2
= (M(Z, A) − M(Z − 1, A)) c2 − 2me c2 ≥ 0.
3. Elektroneneinfang (engl. electron capture, EC):
Wenn β+ -Zerfall energetisch nicht möglich ist:
A
ZX
EC
A
+ e− → Z−1
Y + νe ,
das Elektron stammt dabei aus der Atomhülle (meistens aus der K-Schale), Ψ(r =
0) & 0.
Fundamentaler Prozess:
νe
e−
u
u
d
p
d
u
d
n
Energiedifferenz:
∆E = ((M(Z, A) − Zme ) + me − (M(Z − 1, A) − (Z − 1)me ) − me ) c2 + ε
= (M(Z, A) − M(Z − 1, A)) c2 > 0.
Der Term ε entspricht der Anregung des Tochterkerns.
B:
7
EC
Be → 7 Li + νe + 8, 6keV,
t=53d
7
Be ohne Elektronenhülle ist stabil.
Indirekter Nachweis des Neutrino von Rodenback und Allen (1952):
K-Einfang des 37 Ar:
36
EC 34
Ar →
t=35d
Cl + νe + 0,
MeV
| 82{z
}.
=Q
Kinematik: 37 Ar ist in Ruhe ⇒ E ν + E Cl = Q, pν + pCl = 0.
2
Mit p2Cl = c12 (E 2 − (m0 c2 )2 ) = c12 (E kin
+ 2E kin m0 c2 ) folgt:
1
2E Cl mCl c2
c2
1
p2ν ≈ 2 E ν2 (da mν ≈ 0)
c
2E Cl mCl c2 ≈ Q2
p2Cl ≈
⇒E Cl =
Q2
= 9, 7eV
2mCl c2
3.1 Radioaktivität
33
Ar
Signal: e−
++
+
Cl+
11
00
00
11
(2)
−
γ
5kV
+
(1)
Auger−Elektron
Signal: Cl+
Abbildung 24: Links: Das Cl+ wird bei (1) gemessen, dass Auger-Elektron bei (2). Rechts:
Erzeugung des Auger-Elektrons.
Der Messprozess läuft wie folgt ab: Nach dem EC fällt ein Elektron aus einer höheren Schale in die K-Schale. Dabei wird ein Photon abgstrahlt, das ein Elektron (das
Auger-Elektron) aus der Hülle des Atoms löst. Das Cl+ wandert zum negativ geladenen Gitter.
4. Doppelter β-Zerfall:
A
ZX
A
→ Z+2
Y + 2e− + 2νe
(gg-Kerne, die aus energetischen Gründen nicht in uu-Kerne zerfallen können).
B:
76
Ge → 76 Se + 2e− + 2νe
5. Sonderfall: neutrinofreier doppelter β-Zefall (bislang nicht beobachtet):
A
ZX
A
→ Z+2
Y + 2e −
Erklärung: ν = ν (Majorana-Neutrinos).
u
d
W−
Spin −
Spin +
d
e−
e−
W−
u
Problem: ∆L = 2 (L =Leptonenzahl). Helizität nicht erhalten (der Spin müsste
umklappen).
Die Fermi-Theorie des β-Zerfalls:
34
3 Kernumwandlung
1. Ausgangspunkt: Fermis Goldene Regel. Reaktionsrate pro Target:
W=
2π 2 2 dn
G |M|
,
~ F
dE 0
dabei ist G F = 1, 16 · 10−5 /GeV2 (mit ~ = 1 = c) die Kopplungskonstante, |M|2 =
dn
|h f |H |ii|2 das Matrixelement und dE
die Zustandsdichte im Phasenraum.
0
2
2
Für β-Zerfall: q ≪ mW
|M|2 ≈ 1 für ↑n →↑p + ↓e− ↑ν
2
|M| ≈ 3 für ↑n →↓p + ↑e− ↑ν
(Fermi-Übergang)
(Gamow-Teller-Übergang)
2. Im Phasenraum: X → Y + e− + νe .
E e + E ν = E 0 (= E max ), denn E Y ≪ E e , E ν .
1
1
⇒ pν = (E 0 − E e ), dpν = dE 0
c
c
2
2
V4πpe dpe
Vp
dne = 2 e3 dp =
2π ~
h3
(vν ≈ c)
(für ein Teilchen gilt: ∆x∆y∆z∆p x ∆py ∆pz = h3 ).
dn2e
dne dnν
=
dE 02
dE 02
16π2 p2e p2ν
= V2
dpe dpν
h6
16π2
= V 2 6 2 p2e (E 0 − E e )2 dpe
hc
W = n(pe )dpe ∼ p2e (E 0 − E e )2 dpe .
Zusätzliche Faktoren:
• Berücksichtige Coulomb-Wechselwirkung im Kern: f (Z, pe).
q
2
νc
)2 .
• Berücksichtige Neutrinomasse: 1 − ( Em0 −E
e
Wie bekommt man pe ? Siehe Abb. 26.
Experimenteller Nachweis des Neutrinos:
Reimes, Cowan (1953...1959): Neutrinostrahlung (mit 1013 ν/cm2 s) bekam man aus dem
Savanna River-Reaktor. Der Detektor (Abb. 27) befand sich unter dem Reaktorkern.
νe + p → n + e +
und n + 114 Cd → 115 Cd∗ → 115 Cd + n · γ (je 9, 1MeV)
und e+ + e− → γ + γ (je 511keV)
3.1 Radioaktivität
35
K
Kurie−Plot
für
mν > 0
E0
Ee
Abbildung 25: Die Abweichung von E 0 ist E 0 − mν c2 . So kann man die Masse des Neutrinos bestimmen.
11
00
00
11
00
11
00
11
00
11
00
11
00
11
⊗
⊗
e−
⊗
1
0
0
1
Quelle
11
00
00
11
00
11
00
11
00
11
00
11
00
11
⊗
11
00
00
11
Detektor
(Halbleiterzähler)
Abbildung 26: Bestimmung von pe mit Hilfe eines Magnetfeldes
Es ist Ṅγ ≈ 3/h und
σ(νe + p → n + e+ ) =
Ṅγ
= 10−43 cm2
Akzeptanz · Effizienz
⇒ MFW für MeV-Neutrinos: 100 ly Wasser.
Paritätsverletzung in der schwachen Wechselwirkung
Erinnerung: Naturgesetze sollten P-symmetrisch sein.
Wu (1956): Studium der β− -Emission von 60 Co (die Indizes R bzw. L bezeichnen Rechtsbzw. Linkshändigkeit).
Erwarte: Beim β− -Zerfall ist die Intensität von νR + e−L gleich der Intensität von νL + e−R .
Experiment (Abb. 28):
• Ausrichtung des 60 Co im Magnetfeld H. T ≈ 0, 01K, damit kT < µI · B.
36
3 Kernumwandlung
1.Szintillator
γ
−
ν
e+
H 20 + Cd Cl 2
p
(200kg)
γ
2.Szintillator
Abbildung 27: Neutrinodetektor
Szintillatoren
e−
γ1
H
0
1
0 Co(60)
1
11
00
γ2
00
11
00
11
00
11
00Cer−Mg−Nitrat
11
Abbildung 28: Aufbau des Experimentes zur Paritätsbestimmung
• Kontrolle der Spin-Ausrichtung.
• Zähle e− in Abhängigkeit von T .
Beobachtungen: e− werden bevorzugt entgegen 60 Co-Spin ausgesandt: e−L , νR .
Helizität:
pe · se
−ve
=
<0
| pe | · |se |
c
p · sν
vν
h(ν) = ν
=
>0
| pν | · |sν |
c
h(e− ) =
(L)
(R)
Hintergrund: Schwache Wechselwirkung (W-, Z-Bosonen) nur zwischen linkshändigen
Teilchen, rechtshändigen Antiteilchen.
3.1 Radioaktivität
37
3.1.4 γ-Zerfall
Elektromagnetische Abregung angeregter Kerne.
A ∗
ZX
→ ZA X + γ
Sonderfälle:
• Innere Konversion:
A ∗
ZX
→ ZA X + e−
(Konversionselektron, ähnlich wie Auger-Elektron). Typisch, wenn freie γ-Emission
verboten ist.
B:
72
∗
32 Ge
−
→72
32 Ge + e + 691keV
• Innere Paarbildung:
Emission von e+ , e−-Paaren möglich, falls ∆E B > 2me c2 .
B:
16 ∗
8 O
−
+
→16
8 O + e + e + 6, 06MeV − 1,
| 04MeV
{z }
=2me
Anwendung: Resonanzabsorption von γ-Strahlen = Kernfluoreszenz (Mößbauereffekt).
A ∗
ZX
fällt unter Aussendung von γ auf ein niedrigeres Energieniveau. Der umgekehrte Effekt (d.h. durch Anregung mit γ auf ein höheres Energieniveau) ist bei Kernen
nicht möglich!
Berechne Energien:
1. Rückstoß des Kerns:
Eγ
1
E r = mA v2r =
2
2mA c2
E γ′ = E 0 − E r
B:
57
Fe :
E 0 = 14, 4keV, τ = 1, 4 · 10−7 s ⇒ Γ = 4, 7 · 10−9 eV, E r = 2 · 10−3 eV
(Γ ist die Partialbreite).
2. ZA X + γ′ : Rückstoß des absorbierenden Kerns: E r .
Berücksichtigung der thermischen Bewegung:
38
3 Kernumwandlung
Γ
111
000
000
111
000
111
000
111
000
111
000
111
000
111
000
111
Eγ ’
2 Er
Eo
verfügbar
111
000
000
111
000
111
000
111
000
111
000
111
000
111
000
111
Eγ
E
notwendig
Abbildung 29: E γ notwendig, damit γ′ absorbiert wird
Fluoreszenz möglich
E
Abbildung 30: Dopplerverschmierung macht Fluoreszenz möglich
• Mößbauereffekt (1958): Einbindung in Kristallgitter: Gitterschwingung ⇒ Rückstoßenergie gequantelt.
ca. 60% haben keinen“ Rückstoß (d.h. das ganze Gitter trägt den Rückstoß).
”
Experiment: Abtastung einer natürlichen γ-Linie mit Hilfe des Dopplereffektes.
Erzeugung der γ-Quelle 191 Os aus Neutronenstrahlung eines Reaktors.
191
β
2γ
Os → 191 Ir∗ → 191 Ir + 42keV + 129keV
E γ = 129keV, E r = 4, 6 · 10−2 eV.
Anwendungen:
• HFS-Analysen.
• Isomerieverschiebungen.
• Relativistische Effekte.
Experiment von Pound und Rebka zur Bestimmung des Gewichts von Lichtquanten (1960):
hν
hν
⇒ mγ = 2
c
c
(träge Masse von Photonen = schwere Masse).
p γ = mγ c =
3.1 Radioaktivität
39
Er
1
0
0
1
0
1
0
1
0
1
0
1
1
0
0
1
0
1
0
1
E r− h ν
Abbildung 31: gequantelte Rücktoßenergie beim Mößbauereffekt
Szintillator
.
Nγ
11
00
00
11
Quelle
00
11
00
11
00 γ
11
00 0
0 11
1
1
0 11
1
0
1
00
00
Absorber 11
00
11
00
11
00
11
00
11
.
v
E0
Eγ
Nγ
min.
v [cm/s]
Blei
Abbildung 32: Versuchsaufbau zur Messung von Ṅγ . Minimal bei E 0 .
Bei Fall“ im homogenen Gravitationsfeld erwarten wir:
”
h∆ν
hν
∆E γ = mγ g∆x = 2 g∆x =
c
c
Quelle: 57 Fe: hν0 = 14, 4keV.
2
·20m
erwarte: ∆hν = 14,4keV·9,9m/s
= 3, 1 · 10−11 eV.
9·1010 m/s2
h∆ν
= 2 · 10−15
hν0
bis auf 10% genau nachgewiesen.
3.1.5 Anwendung der Radioaktivität
Altersbestimmung mit der 14 C-Methode:
• In der Atmosphäre läuft folgender Prozess ab:
14
N + p → 14 C + n
(p kommt aus der Höhenstrahlung). Es ist τ(14 C) = 5730a.
Aufnahme des 14 C in organischen Substanzen.
40
3 Kernumwandlung
A
B
Quelle
v
111
000
000
111
000
111
γ
h νο
Gravitation
hν
11
00
00
11
20m
γ
20m
B
11
00
00
11
v
Absorber
A
111
000
000
111
000
111
Detektor
Abbildung 33: Photonen im Gravitationsfeld, vergleiche A und B
• Nach Ende der Stoffaufnahme (z.B. Tod):
14
C → 13 C + e− + νe + 155keV
14
N( C)
R := N(
12 C) ändert sich ⇒ Alter.
R0 = 1, 2 · 10−12 (vor 1950, inzwischen durch verschieden Einflüsse geändert).
3.2 Kernspaltung
3.2.1 Voraussetzungen für spontane Spaltung
Q = M(Z, A) − M(ZX , AX ) + M(ZY , AY ) > 0
Energiegewinn durch Deformation mit Deformationsparameter ε.
ε
R
≈ R(1 − )
a = R(1 + ε), b = √
2
1+ε
r
b
a
Abbildung 34: V = 34 πr3 = 43 πab2
3.2 Kernspaltung
41
Es gilt: Volumen V = const., Oberfläche S = 4πR2 (1 + 25 ε2 + ...). Für die Bindungsenergie
folgt:
2
2
E S = −aS A 3 (1 + ε2 + ...) Oberflächenterm
5
1
Z2
EC = −aC 1 (1 − ε2 + ...) Coulomb-Term
5
A3
!
!
2
Z2
1
aC 1 − 2aS A 3 ε2 > 0
∆E = E(0) − E(ε) =
5
A3
2
aC Z
=X
ˆ s=
>1
2aS A
für spontane Spaltung
2
(Xs ist der Spaltparameter), dies ist erfüllt bei ZA > 51 ⇒ A = 270, Z = 115. Solche
Elemente gibt es nicht (mehr, da sie schon früher zerfallen sind).
∆E
∆E
Element A=270, Z=115
spontan
Uran 238
ε
ε
Abbildung 35: Deformation eines Kerns, im wesentlichen Effekt der Coulombabstoßung
B: In der Natur kommt 238 U vor:
Z2
= 35, 6,
A
ε = 0, 3,
Xs = 0, 7
Für die Spaltung (mit Tunneleffekt) ist t1/2 = 1018 a.
Aber für α-Zerfall nur t1/2 = 4, 5 · 109 a. Die zu überwindende Spaltbarriere ist 6, 3 MeV.
Im Falle von 235
92 U liegt die Spaltbarriere bei 5, 8 MeV.
3.2.2 Uranspaltung
Ausgelöst durch Neutroneneinfang:
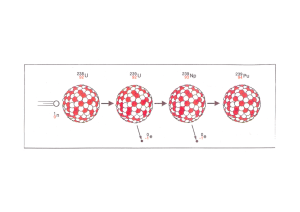
238
235
U + nthermisch → 239 U + 4, 8 MeV
U + nthermisch → 236 U∗ + 6, 4 MeV → X ∗ + Y ∗ + νe + k · n + 204 MeV
X, Y stehen dabei für variable Zerfallsprodukte, häufig kommen z.B.
sind aber etwa 300 Zerfallskombinationen bekannt.
B eines Fragmentes:
β
β 137
137 β 137
Xe → 137
53 I →
55 Cs → 56 Ba
36
Kr, 56 Ba vor, es
42
3 Kernumwandlung
N
X, Y
83
138
Abbildung 36: Häufigkeit der möglichen Zerfallsprodukte X, Y
3.3 Kernkraftwerke
3.3.1 Energiebilanz bei der Spaltung von 235 U

Spaltfragmente
167 MeV




Spaltneutronen
5 MeV 

= nutzbare Energie


prompte Neutronen
6 MeV 



β-, γ-Strahlung der Fragmente 14 MeV 
und nicht nutzbare 12 MeV der ν.
Es entspricht
1g 235 U =ˆ 2MWh thermischer Energie,
1g C =ˆ 8Wh thermischer Energie.
3.3.2 Betrieb durch Kettenreaktion
235
U + n → 236 U∗ → X + Y + 2...4 n(+ν)
→
oder
236
U+γ
Maximiere σSpaltung , damit ein Neutron spaltet und mehr als ein Neutron für weitere Spaltungen freisetzt.
dN
dE
En
1
2
3
4
Abbildung 37: Energie der n, die aus der Spaltung kommen, hE n i = 1, 9 MeV
3.4 Kernfusion
43
Moderator
n
235
n
n
U
111
000
000
111
000
111
235
U
Absorber
Abbildung 38: Ablauf der Kettenreaktion
Der Moderator bremst die Neutronen auf thermische Geschwindigkeiten, um weitere
Spaltungen zu ermöglichen. Der Absorber (z.B. Graphit, Barium) dient zur Kontrolle des
Prozesses.
Die Kettenreaktion ist auch ohne Moderator möglich, wenn die kritische Masse überschritten wird. Im Falle von 235 U sind das ≈ 50kg.
3.4 Kernfusion
• Big Bang
• Sterne, Supernovae
• Wasserstoffbombe
• Reaktoren
3.4.1 Energiegewinnung
Deuterium-Tritium-Prozess:
MeV
d + t → α + n + 3,
MeV
| 1{z
}
| 5{z
} + 14,
für α
für n
Vorteile gegenüber Spaltung: Mehr Energie pro Nukleon; d, t in großen Mengen vorhanden.
Deuterium d: 0, 015% im Wasser (durch Ionisation gewinnen).
Tritium t: n + 63 Li → 42 He + t(+4, 6 MeV), mit t1/2 = 12, 3a.
Voraussetzung für kontrollierte Kernfusion:
• kB T (d, t) > 19keV(⇒ T > 108 K) zur Überwindung der Coulomb-Barriere.
44
3 Kernumwandlung
• Fusionsrate pro Volumen:
Ṅ = nd · nt · hv · σ(t, d)i =
n2
hv · σ(t, d)i
4
v ist die relative Geschwindigkeit, nd bzw. nt ist die Teilchendichte von d bzw. t und
n = nd + nt = ne .
⇒ Leistungsdichte
Pd,t
!
√ 2
= Ṅ · Qd,t > PVerlust = gn T
Aufheizung des Plasmas durch α und Energie der n. Verluste entstehen z.B. durch
die Bremsstrahlung der e− im Plasma.
⇒ Zündparameter
Z = n · τE · kB · T
τE ist die Einschlusszeit. Für Z > 1021 keVs/m3 ist Fusion möglich.
3.4.2 Reaktortypen
1. Magnetischer Einschluss: Erhitztes Plasma wird durch starke Magnetfelder einige
Sekunden lang festgehalten.
Ansätze:
• Stellarator
• Tokamak (1952 von Tamm und Sacharow)
B: JET (Joint European Torus)
n = 1020 /m3 , kB T = 15keV, τE > 1s.
⇒ Z = 1, 5 · 1021 keVs/m3 .
Leistung im Betrieb: 1, 7MW.
2. Laser-induzierte Fusion (Inertialfusion), Abb. 39:
d,t gefroren
Laser
t
d
t
d
t d t
d t d
t d t
t d
d
Glasmantel
100 µm
Abbildung 39: Laser-Beschuss von Pellets“
”
3.4 Kernfusion
45
• Erhitzung auf 108 K innerhalb von 10−8 s durch Laserbeschuss.
• Abdampfung des Glases.
• Hundertfache Verdichtung von d, t durch Stoßwelle.
B: Shiva-Nova Laser im Livermore Lab.

nd , nt > 1022 /cm3 



−8
τE > 10 s 
⇒ Z > 1022 keV s/m3



T > 108 K
3.4.3 Energiegewinnung in Sternen
Betrachte die Sonne:
Korona
γ
Photosphäre
Konvektionszone
γ
Kern
Strahlungszone
γ
Abbildung 40: Aufbau der Sonne
auf der Erde (Solarkonstante).
P = 1, 4 kW
m2
Abstand 1AE = 150 · 106 km.
⇒ P⊙ = 4 · 1023 kW.
∅Sonne = 9, 4 · 106 km.
T = 5800K.
Betrachte den Kern der Sonne:
T ≈ 15, 6 · 106 K, P ≈ 1011 bar, ̺ ≈ 141 cmg 3 .
Energieerzeugung:
46
3 Kernumwandlung
1. pp-Zyklus (98, 4%):
Am Anfang:
p + p → d + e+ + νe + 1, 19 MeV
p + p + e → d + νe + 1, 44 MeV
dann:
d + p → 3 He + γ + 5, 49 MeV
3
He + 3 He → 4 He + p + p + 12, 85 MeV
Das zuletzt entstandene pp-Paar kann wieder zu der ersten Reaktion beitragen.
2. CNO-Zyklus (1, 6%):
Zuerst:
12
C → 13 N + γ
→ 13 C + e+ + νe
dann:
13
C + p → 14 N + γ
und
14
N + p → 15 O + γ
→ 15 N + e+ + νe
und
15
12
N + p → 12 C + 4 He
C + 4p → 12 C + 4 He
3.5 Wechselwirkung von Strahlung mit Materie
Energieverlust/Absorption durch:
Elektromagnetische Wechselwirkung mit Atomhülle oder Atomkern (z.B. e− , e+ , µ+ , µ− , γ).
Hadronische Wechselwirkung mit Atomkern (z.B. π+ , π− , p, n, p, n, K+ , K− , K0 ).
3.5.1 Energieverlust für geladene Teilchen
Vorgang: Ionisation.
Klassische Beschreibung durch Bohr.
Quantenmechanische Beschreibung durch Bethe.
(Moderne) relativistische, quantenmechanische Beschreibung durch Allison und Cobb.
3.5 Wechselwirkung von Strahlung mit Materie
47
dx
dN
dE
dE
E<E 0
E0
E0
Abbildung 41: Energieverlust in dx
e−
Ion
r
b
p
x
Abbildung 42: Wechselwirkung mit Elektron der Atomhülle
Geladenes Teilchen (Ion) erfährt Coulomb-Kraft:
F=
Impulsänderung:
∆p =
ZIon e2
4πε0 (x2 + b2 )
Z
Fdt =
Z
F⊥ dt
(die restlichen Komponenten heben sich weg, da das Problem symmetrisch ist). Also:
Z
1
∆p =
eE⊥ dx
v
(dt =
dx
).
v
Mit dem Gaußschen Satz
Z
EdA = 2πb
A
Z
E⊥ dx =
ZIon e
ε0
folgt
∆p =
1 ZIon e2
.
4πε0 vb
Energieänderung:
1
ZIon e2
∆p2
= 2 2
∆E =
2me 8π ε0 me vb
!2
(∗)
E
48
3 Kernumwandlung
(Energieübertrag des Hüllenelektrons im Abstand b).
Für ne Elektronen pro cm3 :
!
!
Z bmax
2 4
ZIon
e ne
∆p2
bmax
dE = −
· ln
dx
ne 2πbdb dx = −
(∗)
bmin
4πε20 v2 me
bmin 2me
mit bmin =
~
me v
(folgt aus der Unschärferelation) und bmax = ωv .
Quantenmechanisch/relativistisch korrekte Version der Bethe-Bloch-Formel:
!
!
2 4
ZIon
e ne
2me v2
dE
2
2
ln
− ln(1 − β ) − β
=−
dx
hIi(1 − β2 )
4πε20 v2 me
hIi ≈ Z · 1, 44 MeV ist die mittlere Ionisationsenergie.
Bei kleinen (nicht relativistischen) Geschwindigkeiten:
Bei relativistischen Energien (E 0 ≈ 3mIon c2 ):
B: Für 1cm H2 O: dE
≈ 1, 5 MeV.
dx
dE
dx
dE
dx
Z2
∼ ̺ EIon0 .
≈ 1...2̺ MeV
cm2 .
g
Bei hochrelativistischen Energien: relativistischer Anstieg dominiert, gebremst durch Polarisationseffekte im Medium.
Reichweite R im Medium:
hRi =
Z
0
E0
dE
dx
!−1
E 02
1
dE ≈
·
ZIon mIon ̺Absorber
Bragg−Maximum
dE
dx
minimal
ionisierend
<R>
Abbildung 43: Die Verteilung von R
x
3.5 Wechselwirkung von Strahlung mit Materie
49
<R>
1 Tumor
0
0
1
Abbildung 44: Anwendung: Gezielte Bestrahlung eines Tumors
wahrscheinlichster Wert
N dE
dx
Mittelwert
dE
dx
Abbildung 45: mittlerer Energieverlust folgt der Landau-Verteilung
Spezialfall: e+ , e− in Materie.
• Ionisation (Bethe-Bloch)
• Bremsstrahlung nach Ablenkung im Coulomb-Feld der Kerne.
klassisch: a =
F
m
=
ZIon Ze2 1
,I
4πε0 r 2 m Strahlung
∼
ZIon Z 2
m2
∼
dE
dt
=ˆ
Ie−
Ip
=
m2p
m2e
= 3 · 106 .
Energieverlust durch Bremsstrahlung nach der hochrelativistischen Bethe-Heitler-Formel
:
!
dE 4neZ 2 α3 (~c)2 E
187
∼ Z2 E
=
ln
1
dx
me c4
3
Z
dE
dx
Bethe−
Heitler
Bethe−
Bloch
E
Abbildung 46: Verlauf der Bethe-Heitler- und Bethe-Bloch-Verteilung
50
3 Kernumwandlung
−
x
= xE0 folgt E(x) = E 0 e x0 . Der Proportionalitätsfaktor x0 heißt Strahlungslänge
Aus − dE
dx
und ist ein Maß für die Absorptionsfähigkeit.
B:
x0 (Al) = 9cm
x0 (Fe) = 1, 8cm
x0 (Pb) = 0, 56cm
3.5.2 Coulomb-Streuung
Einfache Streuung (vgl. 2.1):
dσ
ZIon Ze2
=
dΩ
4πε0 4E 0
!2
·
1
(sin 2θ )4
Vielfachstreuung:
Wahrscheinlichkeit für Streuwinkel folgt der Normalverteilung:
θ2
1
w(θ) = √
e− 2θrms
2πθrms
mit Streuung
θrms
21 MeV
= √
2pβc
r
x
,
x0
wobei x die Eindringtiefe ist.
B: Ein Proton mit Impuls p = 1GeV/c2 in 1m Argon (x0 = 714m):
θrms = 0, 5mrad = 0, 03◦ .
3.5.3 Cerenkov-Effekt
1934: Für geladene Teilchen in Materie mit v > nc (mit Brechungsindex n): Emission von
Cerenkov-Licht.
!
!
Z
dE
4π2 ZIon e2
1
=
1 − 2 2 νdν
dx Cerenkov
c2
βn
B:
H2 O : n = 1, 33
dE
dE
−3
=
0,
4
·
10
MeV/cm,
vergleiche
dx
dx
Cerenkov
Ion
= 2 MeV/cm.
Für β < n1 : keine Cerenkov-Strahlung.
Zahl der Photonen:
2
d2 Nγ 2πZIon
1
e2
1− 2 2
=
2
dxdλ
λ ~c
βn
!
B: 1cm H2 O: Nγ = 500 (z.B. blaues Leuchten im Kühlwasser eines Reaktors).
3.5 Wechselwirkung von Strahlung mit Materie
−
+
51
em−Welle
v
v
θ
Medium
Medium
v < c/n
v > c/n
Abbildung 47: Bei v < nc : kein makroskopisches Dipolmoment; bei v > nc : elektromagne1
tische Welle wird erzeugt mit Geschwindigkeit nc der Wellenfront, cos θ = βn
3.5.4 Wechselwirkung von Photonen
1. Photoeffekt:
σPhoto
mit ε =
4πre2 α2 Z 5
=
ε
Eγ
.
me c2
γ
1
0
0
1
0
1
e−
1
0
0
1
Z
Z
Abbildung 48: Photon löst Elektron aus der Atomhülle
2. Compton-Streuung:
σCompton ∼ Z
ln ε
ε
E’
γ
E
e−
1
0
0
1
Abbildung 49: elastischer Stoß“ zwischen Photon und Elektron
”
3. Paarerzeugung:
wobei E γ > 2me c2 gelten muss.
σPaar ∼ re Z 2 ,
52
3 Kernumwandlung
γ
e−
0
1
0
1
11
00
00
11
00
11
000
111
e+
000
111
Z
000
111
Abbildung 50: Das Photon benötigt einen Stoßpartner zur Paarbildung
σ
Photoeffekt
Compton−Effekt
Paarerzeugung
Eγ
2 m e c2
Abbildung 51: Vergleich von σPhoto , σCompton und σPaar
3.5.5 Hadronische Wechselwirkung in Materie
Für uns relevant: Langlebige Hadronen
p, n, p, n
π+ , π− , K+ , K− , K0long
Geladene Hadronen: Energieverlust durch elektromagnetische Wechselwirkung:
Hadronische Wechselwirkung:
Hadron + Kern → Kernfragmente + Hadronen
h
oder
h
π+
1
0
0
1
π−
π0
K− K+
Abbildung 52: Hadronische Wechselwirkung
γ
dE
.
dx C
3.6 Strahlenwirkung, Dosimetrie
53
Bei hohen Energien:
Hadron + Kern → Kernfragmente
+ n · [π+ , π− , π0 ]
n
· [K+ , K− , K0long , K0short ]
+
10
+ einige % Baryonen, Antibaryonen
Maß für die Absorption:
Nukleare Absorptionslänge λ =
A
,
σNL ̺
Einheitcm.
x
N(x) = N0 e− λ .
B: Vergleiche hadronische und elektromagnetische Wechselwirkung.
C : λC = 34cm x0,C = 19cm
Fe : λFe = 17cm x0,Fe = 1, 8cm
U : λU = 11cm x0,U = 0, 3cm
3.6 Strahlenwirkung, Dosimetrie
1. Allgemeine Begriffe:
Aktivität:
dN
,
dt
Einheit: 1 Becquerel (Bq) =
Energiedosis: DE =
Dosisrate:
dDE
,
dt
∆E
,
∆m
1 Zerfall
s
Einheit: 1 Gray (Gy) =
= 0, 27 · 10−10 Curie (Ci).
J
kg
= 100 rad.
Einheit: Gy/s.
2. Für ionisierende Strahlung:
Ionendosis: DQ =
∆Q
,
∆m
Einheit: 1 Röntgen (R) = 2, 6 · 10−4 As
.
kg
3. Biologische Wirkung:
Äquivalenzdosis: H = qDE , Einheit: 1 Sievert (Sv) = 1qGy = 100rem. Der Faktor
q wird biologischer Wirkungsfaktor oder Qualitätsfaktor genannt.
B:
• Qualitätsfaktoren:
Teilchen
γ, e− , e+
n
p
α, Kernfragmente
q
1
5...20
5...20
20
• Energiedosiswerte:
Quelle
mSv/a
kosmische Strahlung
0, 3
natürliche Radioaktivität
0, 5
eingenommene Radioaktivität
0, 3
54
3 Kernumwandlung
• Gesetzlich vorgeschriebene Grenzwerte:
Organ
mSv/a
Gebärmutter, Keimdrüsen
0, 3
Haut
1, 8
übrige Organe
0, 9
tödlich innerhalb von 30 Tagen: 3 Gy = 300 rad.
55
4 Detektoren und Beschleuniger
Wichtigste Werkzeuge der Teilchenphysik:
Beschleuniger: Studium hochenergetischer Reaktionen; Erzeugung neuer Teilchen aus
kinetischer Energie.
Detektoren: Nachweis von Teilchen aller Art.
4.1 Detektoren
Allgemein:
Vermessung von
E: Kalorimetrie (Absorption).
p: Richtung, Krümmungsradius im ortsempfindlichen Detektor im Magnetfeld B.
v: Flugzeitmessung oder Cerenkovstrahlung.
m, q: Ionisationsmessung,
dE
.
dx
τ: Zerfallsort im ortsempfindlichen Detektor.
4.1.1 Ionisationsdetektoren
Prinzip: Plattenkondensator mit Medium. Geladenes Teilchen ionisiert Atome,
dE
,
dx
∆E
,
=n=
WIon
∆E = ∆x
ne− = nIon
dabei ist WIon die effektive Ionisationsenergie.
Spannungsänderung:
1
1
CU 2 = CU02 −
2
2
Z
d
U0
1
neEdy = CU02 − ne (d − y0 )
2
d
y0
!
ne d − y0
(mit U + U0 ≈ 2U0 )
⇒∆Ion U = U − U0 = −
C
d
ne y0
Elektronen: ∆e U = −
C d
ne
insgesamt: ∆U = ∆Ion U + ∆e U = − .
C
Ionen:
56
4 Detektoren und Beschleuniger
y
−U0
d
y0
+
+
+
+
+
+
−
−
−
−
−
− geladenes Teilchen
x
∆x
R
C
Abbildung 53: Ionisationsdetektor
∆U
te
t Ion
ve
−(ne y0 ) / (Cd)
~e −t / RC
v Ion
−ne / C
t
Abbildung 54: Realistisch: Aufladen über R: ∆U ∼ e− RC
Signalform:
∆e U = −
ne ve t
,
C d
∆Ion U = −
ne vIon t
C d
B: R = 1MΩ, C = 100pF ⇒ RC = 100 µs (d.h. Verfälschung des Signals, aber
trotzdem gut genug).
Signal: ∆E = 1 MeV, WIon = 2GeV ⇒ ∆U = 60 µV.
4.1.2 Gasdetektoren
Charpak (Nobelpreis), Sauli: CERN-Report 77-09 (Klassiker!). Zur Ortsmessung eingesetzt.
1. Zählrohr:
B: U0 = −2kV, ri = 50 µm, ra = 1cm ⇒ E(ra ) = 75kV/cm.
4.1 Detektoren
57
−U0
E(r)
ri
+
− −
−
+ −
−
+
ra
−
+
−
+
−
+
−
+
Abbildung 55: Aufbau des Zählrohrs (links), Elektronenlawine durch Sekundärionisation
(rechts)
E
~1/r
ri
ra
Abbildung 56: Verlauf des E-Feldes, ri und ra bilden die Grenzen
2. Geiger-Müller-Zählrohr: Sonderfall des Zählrohrs; ≈ 108 Gasentladungen (vgl.
Abb. 57, links).
∆Q = CU0 ,
∆U = U0 .
Auch: Funkenkammer (vgl. Abb. 57, rechts). Gasentladungen werden durch Funken
sichtbar; wird heute nur noch für spezielle Anwendungen eingesetzt.
+
U0 −
C +
+
+
000000
111111
111111
000000
111111
000000
111111
000000
111111
000000
111111
000000
Funken
−
−
−
Abbildung 57: Geiger-Müller-Zähler (links); Funkenkammer (rechts)
3. Proportionalkammer (von Charpak), Abb. 58:
Statt Aneinanderreihung von Zählrohren: “Ummantelung auflösen“.
58
4 Detektoren und Beschleuniger
Kathode
n
Anoden
E −Feld
d
Abbildung 58: Proportionalkammer: In der Nähe zur Anode: E(r) ∼
1
r
Ort des Teilchendurchgangs: Adresse des angesprochenen Drahtes, Streuung σ =
√d ≈ 0, 5mm.
n
Grenzen: Teilchendichte, -rate, Präzision, Volumen
4. Driftkammer (Abb. 59):
111111111111
000000000000
000000000000
111111111111
−−− −
Startsignal (Szintillator)
Stoppsignal (Anode)
Abbildung 59: Dauer des Elektronendrift: Stoppsignal − Startsignal = ∆t
∆t =
vdrift
x
vdrift
= const. ≈ 40...70µm/ns für E > 1, 5keV/cm
Ortsauflösung begrenzt durch ∆t und Diffusion σ ≈ 30...100µm.
5. Zeitprojektionskammer (Abb 60).
4.1 Detektoren
59
11
00
00
11
00
11
00
11
00
11
+
Ortsrekonstruktion
in x, y
−−
− −
− −
Abbildung 60: e− schauert, der Schauer wird wiederum gemessen
4.1.3 Halbleiterdetektoren
Zur Energiemessung eingesetzt. Prinzip: Diode in Sperrichtung.
Si
+
d
Verarmungszone
+
− +
− +
−
n−dotiert
−
p−dotiert
Abbildung 61: typisch: n: 1012 /cm3 Phosphor (Donator); p: 1015 /cm3 Bor (Akzeptor)
Signalhöhe: Energie zur Erzeugung eines e− -Loch-Paares: WIon (Si) = 3, 6eV,
Si = 3, 9MeV/cm.
⇒ für d = 300µm: 33000e−-Loch-Paare (Signal muss verstärkt werden).
Ortsbestimmung: Verstärker anschließen, Signale mitteln. σ x =
√d
2
dE
dx
von
≈ 10...20µm.
4.1.4 Szintillationsdetektoren
Prinzip:
Szintillator: Ionisation → Lichtemission.
Photodetektor: Licht → Photoelektron → Stromsignal
1. Anorganischer Szintillator:
Kristall mit sogenannten Aktivatoren. Hohe Lichtausbeute ⇒ hohe Energieauflösung.
B: NaJ + Tl: ̺ = 3, 7g/cm3 , λSz = 410nm, Nγ /MeV = 4 · 104 .
2. Organischer Szintillator:
Prinzip: Ionisation → Molekülanregung → Emission (von UV-Licht).
60
4 Detektoren und Beschleuniger
1
0
0
1
0e−
1
0
1
γ
Szintillator
Signal
Lichtleiter
Abbildung 62: Licht erzeugt Photoelektron; Photoelektron erzeugt Stromsignal; Anstiegszeit des Signals im Bereich ns
6...8 eV
1111111
0000000
0000000
1111111
0000000
1111111
00
11
0000000
1111111
00
11
00Exziton
11
1111111
0000000
0000000
1111111
0000000
1111111
0000000
1111111
Leitungsband
Exzitonband
γ
Energieniveaus
des Aktivators
Valenzband
Abbildung 63: Energie wird an Fremdatome, die Aktivatoren abgegeben, diese wiederum
emittieren Photonen (im UV-Bereich), die auf ein Photokathode treffen
Dotierung mit Wellenlängenschieber → blaues, grünes Licht. Schneller Prozess ⇒
hohe Zeitauflösung.
B: Naphtalen+POPOP: λ = 348nm → 450...500nm (Effizienz ≈ 0, 1).
3. Photomultiplier (PMT):
(dt.: Sekundärelektronenvervielfacher (SEV)) siehe Abb. 64. Detektieren die Pulse
von Szintillatoren. Erreichen hohe Zeitauflösungen von ≈ 100 − 200 ps.
∆U
1
0
0
1
0
1
0e−
1
Abbildung 64: Photomultiplier; ∆U ≈ 100V
Anwendungen:
• Absorption von e+ , e− , γ: Energiemessung.
4.1 Detektoren
61
• Durchtrittszeit geladener Teilchen; Markierung von Ereignissen ( Triggern“).
”
• Durchtrittsort geladener Teilchen:
Szintillierende Fasern ( Fibers“): Kleine Szintillatoren nebeneinander (∅ ≈ mm).
”
Plastikmaterial
Szintillator
1
0
0
1
Abbildung 65: Fiber: Äußeres und inneres Material haben verschiedene Brechungsindizes
4.1.5 Kalorimetrie
1. Elektromagnetische Kalorimeter: e− , e+, γ.
Prinzip: e− , e+ → Ionisation, Bremstrahlung → γ → Paarbildung → e+ , e− usw. bis
die Energie verbraucht ist
Blei
γ
E0
1
0
0
1
0
1
0
1
0
1
0
1
0
1
0e+
1
0
1
0
1
0
1
0
1
e−
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
1
0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
1
0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
1
0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
1
0
0
1
0
1
0
1
0
1
0
1
0
1
0
0 1
1
0
1
0
1
0
1
0
1
0
0 1
1
0
1
0
1
0
1
0
1
0
1
usw.
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
0 1
1
0
1
1
2
3
4
5
1
0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
d max
Abbildung 66: Schema des elektromagnetischen Kalorimeters
Die Energie halbiert sich bei jeder Paarbildung, nach d Schritten ist die Anzahl
der Sekundärteilchen N(d) = 2d , die Energie eines solchen Teilchens ist E = E2d0 .
Ab einem gewissen dmax werden keine neuen Teilchen gebildet, weil dafür keine
0
Energie mehr vorhanden ist: E krit := E(dmax ) = 2dEmax
, N(dmax ) = EEkrit0 . (Schema in
Abb. 66.)
Form des Schauers (Abb. 67):
∼ d α e−d .
Longitudinal: dE
dd
62
4 Detektoren und Beschleuniger
95%
d E
d d
RM
d
dmax d 95
Abbildung 67: longitudinal (links): bei d95 sind 95% aller Teilchen enthalten; transversal
(rechts): in R M sind 95% aller Teilchen enthalten
0
Transversal: Innerhalb des Moliere-Radius R M = 21x
(x0 =Strahlungslänge) sind
Rkrit
95% der Teilchen enthalten.
dP
max
2d = 2dmax +1 − 1.
Energiemessung: N(d) = 2d , Ntotal =
d=0
0
⇒ dmax = ln(Eln0 /E2 krit ) .
E 0 ∼ ISignal ∼ Ntotal mit E(dmax ) = E krit = 2dEmax
p
√
0)
√
= 3−5%
σ(E 0 ) ∼ Ntotal ∼ ISignal , relativer Fehler: σ(E
.
E0
E
0
B: Bleiglas: E 0 = 100GeV, x0 = 2cm, dmax = 13x0 = 26cm, d95 = 23x0 =
46cm, R M = 3, 6cm.
2. Hadronische Kalorimeter:
Prinzip: Hadron → Kernreaktion ⇄ Sekundärhadronen → Ionisation.
1
etwa π, K → µ, γ(, ν). Wirkungsquerschnitt: σHadron = 40mbA 3 .
Schauerform:
dmax [λ] = 0, 7 + 0, 2 ln(E)[GeV].
√
= 30−80%
R M ≈ 1λ, σ(E)
.
E
E
B: Eisen Fe, E 0 = 100GeV:
dmax = 1, 6λ = 27cm, d95 = 4, 8λ = 80cm, R M = 17cm.
4.1.6 Ältere Technologien
• Funkenkammer (vgl. 4.1.2)
• Blasenkammer: Volumen, gefüllt mit einer Flüssigkeit, die unter Druck (≈ 20bar)
steht. Geladenes Teilchen ionisiert. Bei Druckabfall: Flüssigkeit beginnt bei den
Ionisationskeimen zu kochen → Bläschen.
4.2 Experimente
Systeme von Detektoren zum Nachweis und zur Vermessung von Teilchen und Prozessen.
4.3 Beschleuniger
63
νe
e+
u
νe
X
Z0
u
d
π0
1
0
0
1
d
e−
Abbildung 68: Protonenzerfall (links) und Neutrinonachweis (rechts) sollen im Superkamioka beobachtet werden
ν
50000 t Wasser
Cerenkov−Licht
Photo−
multiplier
e−
Abbildung 69: Aufbau des Experiments; Cerenkov-Strahlung im Wasser wird gemessen
• Superkamiokande in Kamioka, Japan
• CMS (Compact Myon Solenoid) am LHC (cmsinfo.cern.ch)
Studium von Ereignissen in pp-Kollisionen bei 14000GeV. Ziele:
– Higgs-Boson finden.
– Supersymmetrien finden.
– Anomalien untersuchen.
– Strukturen der Quarks untersuchen.
– Top-Quark-Physik.
4.3 Beschleuniger
Prinzip:
• Beschleunigung geladener Teilchen in elektrischen Feldern.
• Ablenkung in magnetischen Dipolfeldern.
• Fokussierung durch magnetische Multipolfelder.
64
4 Detektoren und Beschleuniger
4.3.1 Fixed-Target
Schieße Strahlen gegen Streukörper.
11
00
00
11
00
11
00
11
ν
m2
11
00
00
11
00
11
00
11
µ
Detektor
p
m1
Abbildung 70: Mehrere Targets werden beschossen, m1 = mp , m2 =Masse des Targets
Schwerpunktenergie:
q
p
√
S = m21 + m22 + 2E 0 m2 ≈ 2m2 E 0
Hohe Ereignisraten, einfacher Detektor, 100% Akzeptanz (d.h. alle Sekundärteilchen können
vermessen werden).
√
B: CERN SPS: pp bei 450GeV: S = 29GeV.
4.3.2 Collider
Schieße beschleunigte Teilchen gegeneinander. So kann man eine höhere Schwerpunktenergie erreichen als bei Fixed-Target.
Schwerpunktenergie:
q
p
√
S = m21 + m22 + 2E 1 E 2 − 2 p1 · p2 ≈ 2 E 1 E 2 (= 2E 1 , wenn E 1 = E 2 )
Niedrige Ereignisraten, hohe Anforderungen an den Detektor, Akzeptanz unter 100%.
√
B: Fermilab Tevatron: 980GeV pp-Kollision, S = 1960GeV.
Die Luminosität L ist
L=
Np Np
f nBunch
4πσ x σy
Die p und p werden in Teilchenpakten, den Bunches, aufeinandergeschossen. Np bzw. NP
ist die Anzahl der jeweiligen Teilchen pro Bunch, f ist die Frequenz der Bunches. Die
Teilchen sind ungefähr gaußförmig in x- und y-Richtung im Bunch verteilt, σ x bzw. σy
geben die Streuung an. Je kleiner σ x , desto höher die Dichte im Bunch, und desto höher
die Kollisionsrate.
4.3 Beschleuniger
65
Detektor
Abbildung 71: Zwei Bunches“werden gegeneinander geschossen.
”
Damit ist die Ereignisrate im Detektor: Ṅ = Lσpp .
Wahrscheinlichkeit einer Wechselwirkung (für ein Proton) beim Aufeinandertreffen zweier Bunches:
σpp Np
,
wp =
F
dabei ist F die Querschnittsfläche des p-Bunches.
Wechselwirkungsrate (für ein Proton):
σpp Np
f.
F
Für Np Protonen:
Ṅ =
σpp Np Np
f.
F
Die integrierte Luminosität ist
N = σpp
Z
Ldt [pb−1 ].
B: Tevatron (2003)
c
Np = 1011 , Np = 1011 , nBunch = 6, f = 2πR
≈ 48kHz, σ x = σy = 50µm
31
2
⇒ LTev = 10 /cm s.
Rate von pp-Kollisionen:
σinelast = 50mb = 5 · 10−26 cm2 , Ṅ = σinelast L = 5 · 10−26 cm2 · 1031 /cm2 s = 500kHz.
Rate von Top-Quarks (uu → tt):
σtt = 7pb = 7 · 10−26 cm2 , Ṅtt = 7 · 10−5 Hz, d.h. in einem Teilchenphysik-Jahr“ von 107 s:
”
R 107 s
R 107 s
1
Ntt = 0 Ṅdt = 700 und 0 Ldt = 100pb
.
66
5 Elementarteilchenphysik
5 Elementarteilchenphysik
5.1 Grundlagen
5.1.1 Der Teilchenzoo
1. Bis in die 1930er Jahre bekannte Teilchen: p, n, e−, ν und ihre Antiteilchen.
2. Pion π:
1935 Yukawa: Kurze Reichweite der Kernkraft: Austausch eines Teilchens mit Masse.
π0
n
n
p
p
p
n
π−
n
p
Die Kernkraft wird durch das Yukawa-Potential beschrieben:
g −r
V(r) = − e r0
r
mit r0 = 1, 4 · 10−15 m =
~
mπ c
⇒ mπ = 140 MeV/c2 .
1947 Powell: π in der Höhenstrahlung gefunden.
1950 Chamberlain: Bestimmung der Lebensdauer τπ± .
n
Blei
1
0
0
1
0
1
e−
π+
γ
p
Abbildung 72: Erzeugung von π+
Signal
Detektor
µ
π+
1
2
1
e+
2
3
∆ tµ
∆ te
3
∆ tπ
t
Abbildung 73: π+ wird im Detektor abgebremst, zerfällt in ein µ, dieser wiederum zerfällt
in ein e+ . Die Lebensdauer wird anhand der Zerfallsstrecke bestimmt
t
N(t) ist exponentialverteilt: N(t) = N0 e− τ mit τµ = 2, 2 · 10−6 s und τπ = 2, 6 · 10−8 s
5.1 Grundlagen
67
Bestimmung des Spins von π:
Vergleiche die Wirkungsquerschnitte σ1 := σ(p + p → π+ + d) und σ2 := σ(π+ + d →
p + p). σ ist proportional der Anzahl der Endzustände inklusive Spin. Mit Jp = 12
und (Jd = 1) folgt:
σ1 ∼ (2Jπ + 1)(2Jd + 1) ∼ 3(2Jπ + 1)
1
σ2 ∼ (2Jp + 1)2 = 2 (Faktor 1/2 wegen des Pauli-Prinzips)
2
Daraus ergeben sich folgende Möglichkeiten:
(3
σ1
falls Jπ = 0
= 29
falls Jπ = 1
σ2
2
Experimentell stellt sich heraus, dass Jπ = 0 zutrifft.
3. Myon µ:
1937 Anderson: Bei der Suche nach π wird das µ in der Nebelkammer gefunden.
mµ = 106 MeV/c2 und τµ = 2, 2 · 10−6 s.
Rabi: Who ordered that?“
”
4. Kaon K:
1947 Butler, Rochester:
π+
K0
π−
π
π+
K+
π0
Abbildung 74: Kaonenerzeugung und -zerfall
Strangeness: Beschreibt die Tatsache, dass Kaonen zwar durch die starke Wechselwirkung erzeugt werden, aber nur durch die schwache Wechselwirkung zerfallen, obwohl ihre Zerfallsprodukte ebenfalls stark wechselwirkende Teilchen sein
können. Lebensdauer τK ≫ 10−23 s.
mK± = 494 MeV/c2 , τK± = 1, 2 · 10−8 s
mK0 = 498 MeV/c2 , τK0short = 9 · 10−11 s
τK0long = 5 · 10−8 s
Zerfälle:
65%
(−)
K± → µ± + ν µ
21%
→ π± + π0
68
5 Elementarteilchenphysik
K0long → π+ + π− + π0
→ 3π0
10−3 %
→ 2π0 ; π+ π−
K0short → π+ + π−
→ 2π0
10−3 %
→ 3π0 ; π+ π− + π0
5.1.2 Fundamentale Teilchen des Standardmodells
Materieteilchen Fermionen: Spin 12 .
1. Leptonen:
−
−
−
e ,µ ,τ
νe , νµ , ντ
Ladung Q
−1
0
Wechselwirkung
elektromagnetisch, schwach, Gravitation
schwach, Gravitation
und ihre Antiteilchen e+ , µ+ , τ+ , νe , νµ , ντ .
2. Quarks:
Ladung Q
u, c, t
d, s, b
2
3
− 31
Wechselwirkungen: elektromagnetisch, schwach, stark, Gravitation.
5.1.3 Zusammengesetzte Objekte
B:
• Elektromagnetisch gebundene:
H: p mit e− in der Schale.
Das Positronium e− e+ .
Ein myonisches Atom mit µ− (statt e− ) in der Schale.
• Stark gebundene:
Mesonen, z.B. π+ = udd.
Baryonen, z.B. n = udd, Λ = uds.
Exoten (Existenz nicht wirklich bewiesen): Glueball (nur Gluonen g), Hermaphroditen (z.B. qqg).
5.1 Grundlagen
69
1. Klassifizierung der Hadronen durch Quantenzahlen:
Spin J
Ladung Q
Isospin I
Baryonenzahl B
Strangeness S
• Isospin (Heisenberg)
Zustände |I, I3 i; Isospin erhalten in starken Prozessen.
Dublett:
+
+
1 1
1 1
n = , −
p = ,
2 2
2 2
Triplett:
π+ = |1, 1i
π0 = |1, 0i
π− = |1, −1i
• Baryonenzahl: B = 1 für Baryonen, B = −1 für Antibaryonen, B =
Quarks, B = 0 für Mesonen.
B(π) = 0
B(n) = B(p) = +1
1
3
für
B(n) = B(p) = −1
• Strangeness: Nur für Teilchen, die s-Quarks enthalten. S = 1 für s, S = −1
für s. Für π, n, p ist S = 0.
S (K+ ) = +1 S (K− ) = −1
S (Λ) = −1
S (s) = −1 S (s) = +1
Zusammenhang der Quantenzahlen:
B S
Y
Q
= I3 + + =: I3 +
e
2 2
2
mit Hyperladung Y = B + S .
Mesonen mit Spin 0, Quark-Antiquark-Paare (Abb. 75)
K0 = ds
K+ = us
K− = us
0
K = ds
π+ = ud
π− = ud
π0 = uudd
η = uuddss
70
5 Elementarteilchenphysik
Y
1
K0
π−
Strangeness
K+
π0 η
+1
π+
I
−1
−1/2
K−
1/2
1
K0
−1
Abbildung 75: Mesonenoktett
Baryonen mit Spin 21 , drei Quarks (Abb. 76)
n = udd
p = uud
Σ− = dds
Σ0 = uds
Σ+ = uus
Ξ− = dss
Ξ0 = uss
Λ = uds
Baryonen mit Spin 32 , drei Quarks (Abb. 77)
∆− = ddd
∆0
∆+
∆++
Σ−
0
= ddu
= duu
= uuu
= dds
Σ0 = uds
Σ+ = uus
Ξ− = dss
Ξ0 = uss
Ω− = sss
−1
5.1 Grundlagen
71
Y
n
p
1
Σ−
0
Σ0 Λ
−1
Σ+
−1/2
1/2
−1
Ξ−
Strangeness
I
−1
1
Ξ0
−2
Abbildung 76: Baryonenoktett
Vorhersage: Es gibt ein Baryon Ω− mit Spin 32 , Strangeness S = −3 und mΩ− ≈
m∆ + |S | · 150 MeV. Im Jahr 1964 wurde Ω− gefunden.
2. Das statische Quarkmodell von Gell-Mann und Zweig (1964):
Hadronen zusammengesetzt aus u, d, s-Quarks (Spin J = 12 , Baryonenzahl B = 13 ):
Flavour
u
d
c
s
t
b
Es ist
Q
e
Ladung Q
2/3
−1/3
2/3
−1/3
2/3
−1/3
Isospin I
1/2
1/2
0
0
0
0
I3
Strangeness S
1/2
0
−1/2
0
0
0
0
−1
0
0
0
0
Charm
0
0
1
0
0
0
= I3 + 21 (B + S ).
B: u-Quark:
Q
e
=
1
2
+ 12 ·
1
3
= 32 .
3. Der Farbfreiheitsgrad:
∆++ (uuu) ist symmetrisch in Flavour, Spin ↑↑↑ und wegen Bahndrehimpuls ℓ = 0
auch symmetrisch im Raum. Dies scheint ein Widerspruch zu sein, da es keine
vollständig symmetrischen Teilchen geben darf (die totale Wellenfunktion muss
antisymmetrisch sein)! Es muss also einen zusätzlichen Freiheitsgrad geben, den
Farbfreiheitsgrad (vgl. Abb. 78):
Quarks: blau, grün, rot
Antiquarks: blau, grün, rot
Hadronen sind farbneutral.
72
5 Elementarteilchenphysik
Y
∆−
∆0
∆+
∆++
−1
Strangeness
0
Σ0
Σ−
−3/2
1
Σ+
−1/2
1/2
Ξ−
1
I
3/2
Ξ0
Ω−
−1
−1
−2
−2
−3
Abbildung 77: Baryonendekuplett
B:
π = ud : rot rot
p = uud : rot grün blau (= weiß“)
”
Farbneutrale Baryonen:
r
1 ( rot, grün, blau − rot, blau, grün + blau, rot, grün
|qq′ q′′ i =
6
− blau, grün, rot + grün, blau, rot − grün, rot, blau )
Starke Wechselwirkung: Beziehung zwischen Farbobjekten.
5.1.4 Fundamentale Wechselwirkung
1. Elektromagnetische Wechselwirkung (Quantenelektrodynamik):
Kräfte durch Austausch virtueller Photonen.
2
• Photoeffekt mit der Kopplungskonstanten αem = 4πεe 0 ~c .
√
√
√
• Rutherford-Streuung mit α ∼ e, Streuamplitude A(q) = α q12 α =
e2
4πq2
.
• Bremsstrahlung.
α
q2
=
5.1 Grundlagen
73
antigrün
rot
blau
antiblau
rot
grün
blau
antiblau
blau
antirot
grün
Abbildung 78: Aus der Kombination einer Farbe mit ihrer Antifarbe ergibt sich ein farblosser Zustand. Aus der Addition der drei verschiedenen Farben ergibt sich gleichfalls ein
farbloser Zustand.
• Selbstenergiebeiträge (Teilchen koppelt mit sich selbst).
Geladene Teilchen: Gebundene Systeme, V ∼ αr . Potential V bestimmt durch Messung der Energieniveaus (Spektroskopie).
2. Starke Wechselwirkung (Quantenchromodynamik):
Austausch masseloser Gluonen. Kopplungskonstante αs =
pulsüberträge q2 < 0, 5 GeV2 gilt g s = 1.
g2s
.
4π~c
Für kleine Im-
Gebundene Systeme für Quarks: Hadronen.
αs hängt vom Impulsübertrag q2 ab. Für kleine Abstände, also große q2 wird die
Kopplung der Quarks untereinander kleiner und verschwindet asymptotisch (asymptotische Freiheit). Umgekehrt wächst die Kopplungsstärke zwischen den Quarks
bei großen Abständen so stark, dass einzelne Quarks nicht aus dem Hadron entfernt
werden können (Confinement).
3. Schwache Wechselwirkung (Quantenflavourdynamik):
Austausch von Bosonen mit Masse.
νe
e−
u
e+
W+
W+
u
u
d
p
d
u
d
n
g2
4π~c
≈
1
30
Pionzerfall
> αem .
Der Propagator bestimmt die Stärke der Wechselwirkung:
q2
1
,
+ m2
e−
Z0
νe
d
Neutrino−Nukleon−Streuung
αw =
e−
p
elastische Streuung
p
74
5 Elementarteilchenphysik
2
m = mW bzw. = mZ . Streuamplitude: f (q) = q2g+m2 . Obwohl αw > αem gilt, ist
die schwache Wechselwirkung aufgrund der hohen Massen der W- und Z-Bosonen
schwächer als die elektromagnetische.
Für q → 0: GF =
g2
m2W
≈ 10−5 GeV−2 = const.
4. Gravitation:
vergleiche
F m1 m2
=
F q1 q2
αgrav =
Gm2p
~c
Gm1 m2
r2
q1 q2
4πε0 r 2
(= 6 · 10−38 für p, e−)
= 6 · 10−39 .
5. Laufende Kopplung:
−
+
+
Abbildung 79: Vakuumpolarisation (QED): Großer Abstand =ˆ kleiner Impulsübertrag
q2 : Probeladung sieht abgeschirmte Zentralladung, Wechselwirkung wird schwächer mit
größerem Abstand
5.1.5 Farbe und Gluonen
1. Indirekt: Existenz von ∆++ : uuu, ↑↑↑, ℓ = 0, rot blau grün.
2. Messung des Wirkungsquerschnitts von
e+ + e− → q + q + Hadronen
und von
e+ + e− → µ+ + µ−
ergibt (mit Schwerpunktenergie S )
σqq =
X X 4πα2
q2i
3S
FarbenQuarks i
σµ + µ − =
4πα2
3S
5.1 Grundlagen
75
q
Abbildung 80: Vakuumpolarisation (QCD): Großer Abstand =ˆ große Farbladung: Wechselwirkung wird stärker mit größerem Abstand
und damit für NFarben = 3:
R=
=
X
σqq
= NFarben q2i
σµ + µ −
4 1 1 4 1
+ + + +
3 3 3 3 3
uu
=
dd
ss
cc
bb
11
.
3
3. Anzahl der Gluonen:
Drei Farbfreiheitsgrade, qq-, qqq-Systeme farbneutral.
3 mal 3 Farbkombinationen:


RG, RB, GR






GB, BR, BG

Oktett


√1 (RR − GG)


2



√1 (RR + GG − 2BB)
6
1
√ (RR + BB + GG) Singulett; farbloses Gluon
3
4. Gibt es virtuelle Zustände? Konsistent:
• Lambshift.
• g−2
• laufende Kopplung
76
5 Elementarteilchenphysik
5.1.6 Symmetrien und Erhaltungssätze
Emmy Noether (1917): Jeder Symmetrie (unter gewissen Transformationen) entspricht
eine Erhaltungsgröße.
Kontinuierliche Tranformationen
Transformation
Raumtranslation
Zeittranslation
Rotation
Eichtransformation
Erhaltungsgröße
Impuls p
Energie E
Drehimpuls ℓ
Ladung Q
Diskrete Transformationen
Transformation
Spiegelung
Teilchen-Antiteilchen-Tausch
Zeitspiegelung
Erhaltungsgröße
Parität P
Ladungsparität C
Zeitparität T
1. Parität:
Pψ(r, t) = ψ(−r, t),
P 2 ψ(r, t) = ψ(r, t).
Für Eigenzustände Pψ(r, t) = ±ψ(r, t) gibt es die Eigenwerte P = ±1.
B:
ψ
cos(x)
sin(x)
cos(x) + sin(x)
Pψ
cos(−x) = cos(x) = ψ(x)
sin(−x) = − sin(x) = −ψ(x)
cos(x) − sin(x)
P
1
−1
Pψ , Pψ
2. Ladungsparität (C-Parität):
Naturgesetze gleich für Teilchen und Antiteilchen:
C |Teilcheni = |Antiteilcheni
Die meisten Teilchen sind keine Eigenzustände von C .
B:
Q
µ
p e +2, 79µK
p −e −2, 79µK
J
+ 2~
+ 2~
B
+1
−1
5.1 Grundlagen
77
Erhaltung der C-Parität:
(a) Starke Wechselwirkung:
C (p + p → π− + X) = (p + p → π+ + X)
Wirkungsquerschnitt, Kinematik von π− , π+ gleich (bis auf Promille).
(b) Elektromagnetische Wechselwirkung:
Es gibt π0 → γ + γ:
E
E
C π0 = C |γi C |γi = C 2 |γi = + |γγi = + π0
Gibt es auch π0 → γ + γ + γ?
E
C |γγγi = C |γi C |γi C |γi = − |γγγi = − π0
dies wäre eine Verletzung der C-Parität, der Prozess existiert nicht.
(c) Schwache Wechselwirkung:
π+ → µ+ + νL (↑)
(der Index L steht für Linkshändigkeit, ↑ für den Spin).
Aber
C (π+ → µ+ + νL (↑)) = (π− → µ− + νL (↑))
existiert nicht: Maximale C-Paritätsverletzung!
3. Zeitumkehr:
Invarianz unter Zeitspiegelung: T ψ(x, t) = ψ(r, −t).
B:
Klassisch: Die Gesetze von Newton, F = T F.
Teilchenphysik:
A+B→C+D
⇔
C+D→A+D
4. CP-Symmetrie:
existieren nicht!
P π+ → µ+ + νL (↑) = π+ → µ+ + νR (↑)
C π+ → µ+ + νL (↑) = π− → µ− + νL (↑)
Aber:
gibt es.
C P π+ → µ+ + νL (↑) = π− → µ− + νR (↑)
⇒ alle Wechselwirkungen sind CP-invariant.
78
5 Elementarteilchenphysik
Oder doch nicht?
Christensen, Cronin, Fitch (1964): CP-Symmetrie ist in K-Zerfällen verletzt.
Neutrale Kaonen:
E
E
P K0 = − K0
0 0 P K = − K
E 0 C K0 = K
0 E
C K = K0
0 0 E
C P K = − K
0 E
C P K = − K0
0
(Konvention!)
K -K0 -Mischungen durch folgende Übergänge:
uct
s
W
K0
d
W
s
W
und
K0
uct
d
uct
Gemische:
dann:
Zerfälle:
0 E
1 E 0 K1 = √ K0 − K
2
0 E
1 0 E 0
K2 = √ K + K
2
E
E
1 0 E
C P K01 = √ − K + K0 = + K01
2
0 E
E
1 0 0 E
C P K2 = √ − K − K = − K02
2
Eigenwert + 1
Eigenwert − 1
K01 → π+ + π− oder π0 + π0
E
0 E
C P K1 = C P π+ π− = + K01
K02 → π+ + π− + π0
E
E
E
C P K02 = C P π+ π− π0 = − K02
uct
W
5.1 Grundlagen
79
Aber es wird auch beobachtet:
K01 → π+ + π− + π0
E
E
E
C P K01 = C P π+ π− π0 = − K01
E
im Widerspruch dazu, dass K01 den C P-Eigenwert +1 hat.
⇒ CP-Verletzung!
Mit einer Häufigkeit von 2, 3 Promille tritt auch der Zerfall
0 E
K → π+ + π−
2
auf. Mischzustände:
0 E 0 E
E
Klong = K2 + ε K01
E
0 E 0 E
K
= K − ε K0
2
1
short
(langlebig)
(kurzlebig)
Diese Mischzustände könnten auch für den 3π-Zerfall verantwortlich sein, aber sie
sind keine CP-Eigenzustände, weshalb auch dies zur CP-Verletzung führen würde.
Materie-Antimaterie-Asymmetrie:
( +
)
π + e− + νR
0
Klong → −
π + e+ + νL
Branch ratio = 39%
5. CPT -Symmetrie:
Ist verletzt, wenn z.B. Masse eines Teilchens ungleich der Masse seines Antiteilchens ist, oder die Lebensdauern von Teilchen und Antiteilchen verschieden sind.
Illustration:
π0 ← K+ → |{z}
π+
|{z}
pπ0
pπ+
+
↓P
π ← K+ → π0
↓C
π− ← K− → π0
↓T
π0
π− → K− ← |{z}
|{z}
pπ0
pπ+
Wenn mK− , mK+ , so ist kein Prozess π0 + π− → K− mit den Impulsen pπ+ und pπ0
möglich!
Wenn CPT erhalten ist und da CP verletzt ist, erwarte T -Verletzung (als Ausgleich);
Suche nach elektrischen Dipolmomenten (EDM) qℓ. Betrachte etwa
T
n(Spin ↑, qℓ ↓) −→ n(Spin ↓, qℓ ↓)
Wenn resultierendes EDM gesehen wird:
(∗)
Anzahl n(Spin ↑, qℓ ↓) , Anzahl n(Spin ↓, qℓ ↓) = Anzahl T n(Spin ↑, qℓ ↓)
Wenn ,“ bei (∗) gefunden wird, dann ist die T -Symmetrie verletzt.
”
80
5 Elementarteilchenphysik
5.2 Moderne Teilchenphysik
5.2.1 Struktur der Hadronen
1. Formfaktor:
dσ
dσ
=
dΩ
dΩ
!
Punkt
· |F(q2 )|2
Hofstadter 1956: Elektron-Proton-Streuung, E e = 188 MeV:
|F(q2 )| =
1
(1 +
q2 /0, 71
GeV2 )2
⇒ Rp = 0, 8fm.
2. Inelastische Elektron-Kern-Streuung:
dσ
dΩ
δ
E’
Ee
E
Abbildung 81: Links: Für λe ≈ RKern : E − E ′ = ν =
Elastische Streuung wird seltener.
q2
.
2mKern
Rechts: Für λe ≪ RKern :
3. Tiefinelastische Elektron-Proton-Streuung:
Ee
E0
Ee
Abbildung 82: Links: Protonenresonanzen für λe < Rp . Rechts: λe ≪ Rp : Bei E 0 elastische Streuung an punktförmigen Quarks.
Kinematik: Seien P bzw. Pe die Viererimpulse des p bzw. e, W die invariante Masse
des Systems und ν = E − E ′ .
W 2 = P′2 = (P + q)2 = P2 + 2Pq + q2 = m2p + 2mp ν − Q2
!
!
ν
mp
·
Pq =
Pe − P′e
0
5.2 Moderne Teilchenphysik
81
Elastische Elektron-Proton-Streuung:
2
W = mp ⇒ Q2 = 2mp ν ⇒ 2mQp ν = 1.
Inelastische Streuung:
p
2
ˆ = 0, 1fm, die Größe x heißt
W > mp ⇒ 2mQp ν =: x < 1 ab Q2 = 10 GeV=λ
Bjorken-x.
Beobachtung: Inelastische Streuung hat ein Maximum bei x ≈ 31 .
Interpretation (von Feynman und Bjorken): Bestandteile des Protons: Partonen. Die
Größe x entspricht dann dem Bruchteil des Protonenimpulses, der von einem Parton
getragen wird.
e−
e−
γ
p
Abbildung 83: Tiefinelastische Elektron-Proton-Streuung im Partonmodell
4. Partonverteilung bei der Elektron-Proton-Streuung:
d2 σ
4πα2 E ′ m
2
2
2
2
= 4
F 2 (Q , ν)(cos θ/2) + 2F 1 (Q , ν)(sin θ/2) ,
dq2 dν
q Eν ν
dabei entsprechen die Strukturfunktionen F 1 bzw. F 2 einem magnetischen bzw.
Q2
dν
dx
E
elektrischen Formfaktor. Mit (cos 2θ )2 = 1 − 4EE
′ ≈ 1, ν = x , 1 − y := E ′ :
4πα2
F 2 (x) y2 2xF 1 (x)
d2 σ
=
(1
−
y)
+
dq2 dx
q4
x
2
x
für Q → 0, y → 0:
4πα2
d2 σ
=
dq2 dx
q4
Z
F 2 (x)
dx
x
| {z }
P
daraus:
!
q2i
!
4
1
F 2 (x) = x (u(x) + u(x)) + (d(x) + d(x)) + s(x) + s(x) ,
9
9
u(x), d(x), s(x) sind dabei die Impulsverteilungen der entsprechenden Quarks.
Allgemein zu Lepton-Nukleon-Streuung:
82
5 Elementarteilchenphysik
• elastische Streuung:
dσ 4πα 2 2
F(q
)
=
dq2
q2
• inelastische Streuung:
4πα
d2 σ
= 2 F(x)
2
dq dν
q
Aus Messungen von F 2 (x) bei e + p, e + N, ν + p, ν + N: u(x), d(x), u(x), d(x), ....
Z 1
u(x) + d(x) + u(x) + d(x) + ... xdx, = 0, 50 ± 0, 05
0
aber erwartet: = 1. Der Rest des Nukleonenimpulses wird von Gluonen getragen.
Frage: Sind Quarks punktförmig?
Wenn nicht:
q
WW
q
Abbildung 84: Wechselwirkung von eventuellen zusammengesetzten Quarks
Erwarte nicht
dσ
dΩ
=
αs
,
S
sondern
dσ
dΩ
→ const.(πR2 ).
Falls Neutrino aus Preonen zusammengesetzt:
)
mν ≈ 10 meV mν
< 10−19
V > 1000 GeV V
)
mτ ≈ 100GeV mτ
< 10−1
V > 1000 GeV V
5.2.2 Phänomene der schwachen Wechselwirkung
1. Hochenergetische ν+Nukleon-Streuung.
Vergleiche
νµ + N → µ− + X
und
νµ + N → µ+ + X.
5.2 Moderne Teilchenphysik
83
Beobachtung:
σ
νµ
3
2
νµ
1
2
4
E ν (GeV)
6
Abbildung 85: σ in Einheiten von 10−38 cm2
also σνN ∼ E ν (darf nicht sein!) und σσνN
= 31 . Die schwache Wechselwirkung kopνN
pelt nur an linkshändige Teilchen und rechtshändige Antiteilchen.
Für ν + N hat µ− eine isotrope Winkelverteilung.
Für ν + N hat µ− Vorwärtsrichtung.
Erklärung:
µ+
R
ν µR
µ−
L
ν µL
Spin
Spin
uL
dL
uL
dL
Abbildung 86: Links: Summe der Spins = 1, Vorwärtsstreuung (Helizität des µ!). Rechts:
Summe der Spins = 0, isotrope Winkelverteilung möglich.
Warum ist σνN = 3σνN ?
Wegen der Zahl der möglichen Spinorientierungen!
Angenommen: σνN ∼ E ν ∼ G2F S mit S = 2mν E ν .
Generell: Für punktförmige Streuung von Spin 21 -Teilchen ist
σmax = π
~2 2ℓ + 1
π~2
2π~
=
=
2
2
p 2J + 1 2p m
S
für ℓ = 0, J = 12 .
σ
Unitaritätsgrenze
~
~S
1
S
S
84
5 Elementarteilchenphysik
Widerspruch, wenn Unitaritätsgrenze überschritten wird!
Ausweg: Austausch von massiven Bosonen.
W
√
2
G F = g2 2
8mW
mit mW ≈ 80 GeV/c2 . Für die Kopplungskonstante folgt:
αw =
1
g2
= .
4π 2g
2. Schwache Wechselwirkung von Quarks.
β-Zerfälle, Mesonzerfälle, ν-Nukleon-Streuung: Austausch eines massiven Bosons
mit universeller Kopplung an Quarks und Leptonen.
νe
e−
g2
νµ
g2
µ
u
g2
d
Erwartung
W
W
W
nicht beobachtet:
νµ
e−
νe
W
µ
W
⇒ in der schwachen Wechselwirkung keine Sprünge zwischen Teilchengenerationen (Isospindubletts) bei Leptonen. Andererseits:
Λ → p + e − + νe
K− → µ− + νµ
Aus n-,µ-Zerfällen:
GFn
G Fµ
= 0, 98 , 1.
Cabibbo: Quarks mischen.
Isospindublett:
!
u
u
=
d cos θC + s sin θC
dC
!
5.2 Moderne Teilchenphysik
85
Daraus folgt:
Kopplung u, d ∼ √gs cos θC ,
Kopplung u, s ∼ √gs sin θC
Fn
= (cos θC )2 = 0, 98.
⇒ GG Fµ
Problem: Erwarte folgende Reaktionen:
s
Z0
d
µ+
s
Z0
K long
µ−
d
Branch ratios:
7 · 10−9 % für K0 → µ+ + µ− im Gegensatz zu 64% für K+ → µ+ + νµ .
Vorschlag von
! Glashauer, Illiopolis, Maiani 1970:
Neben
u
auch
dC
!
c
c
=
s cos θC − d sin θC
sC
s
sin θ C
W+
cos θ C
µ+
νµ
u
d
W−
!
µ−
zusätzlich:
cos θ C
c
−sinθ C
Abbildung 87: Oben: Matrixelement M ∼ g2 cos θC sin θC . Unten: M ∼ g2 cos θC (− sin θC ).
86
5 Elementarteilchenphysik
P
M = 0 (Auslöschung durch Interferenz).
P
In Wirklichkeit: M sehr klein, da mc ≫ mu .
⇒
Schwacher Strom:
!
!
d
cos θC sin θC
·
Jw = u c ·
s
− sin θC cos θC
Bei drei Quarkgenerationen:
 
d
 
Jw = u c t · M · s ,
 
b
dabei ist M die Cabibbo-Kobayashi-Maskawa-Matrix. Sie kann beschrieben werden durch drei Winkel und eine komplexe Phase.
Suche nach FCNC ( flavour changing neutral current“):
”
aber dies ist möglich:
µ+
nicht möglich:
µ+
Z
b
W+
s
b
B0
B0
d
µ−
Z
µ−
d
d
W−
tcu
s
d
0
Branch ratio von B0 → K + µ+ + µ− im Standardmodell: ≈ 10−6 .
5.2.3 Elektroschwache Vereinigung
Weinberg, Salam 1967,-68: Vereinigung von elektromagnetischer und schwacher Wechselwirkung.
1. Divergenz in der schwachen Wechselwirkung
1
Erinnerung: G F hat eine Dimension: GeV
2.
νe
e−
e−
νe
5.2 Moderne Teilchenphysik
dσ
dq2
=
G 2F
π
⇒ σνe =
87
G 2F
S
π
⇒ Unitaritätsverletzung bei
⇒ W-Bosonen:
√
S ≈ 600 GeV.
νe
e−
W
νe
e−
Propagator:
1
.
q2 +m2W
2. Weitere Divergenzen: Propagator:
W
gµν −
gµ gν
m2
e
q2 −m2e
W
W
e
W
und
Z
νe
νe
νe
νe
3. Anpassung der Kopplung
e+
e+
W+
e+
W+
W+
Z
γ
e−
νe
und
W−
Nicht divergent, wenn g =
e−
e
, sin θW
sin θW
und
W−
≈ 0, 22 und gZ =
e−
e
.
sin θW cos θW
4. Weitere Divergenzen verlangen ein skalares Boson: Das Higgs-Boson H.
W−
88
5 Elementarteilchenphysik
W
W
W
W
W
W
Z
γ
und
γ
W
Z
und
W
W
W
W
W
W
W
W
H
und
Wenn H existiert: mH < 1, 2 TeV, gH ∼ mTeilchen .
Wie kann man mH bestimmen?
H
t
t
H
W
W
t
W
W
b
⇒ mH < 250 GeV.
Suche nach dem Higgs-Boson (LEP):
e−
Z
Z*
H
b
e+
b
⇒ mH > 114, 5 GeV.
Elektroschwache Eichtheorie → Standardmodell.
Freie Parameter: e, sin θW , mW , mH , die Massen der drei Leptonen, die Massen der
drei Neutrinos, die Massen der Quarks, drei Winkel der CKM-Matrix, eine Phase
der CKM-Matrix, ΛQCD .
Insgesamt 21 freie Parameter.
W
5.3 Astrophysik
89
5.2.4 Offene Fragen
Warum gibt es gerade drei Familien von Quarks?
Wie kommt es zur C-, P- und CP-Verletzung?
Warum gerade Q(u + u + d) = −Q(e− )?
Wie lässt sich die Gravitation einbauen?
Warum gerade 21 Parameter?
5.3 Astrophysik
Elemententstehung im frühen Universum:
• Als das Universum tU ≈ 10−4 s...1 s alt war, betrug seine Temperatur T U = 1012 K...1010 K.
Folgende Prozesse liefen im thermischen Gleichgewicht ab:
e+ + e− ↔ γ + γ
p + e − ↔ n + νe
n + e + ↔ p + νe
Das Verhältnis von Protonen und Neutronen folgt aus der Maxwell-BoltzmannVerteilung:
!
mn − mnkT−mp
Nn
.
e
=
Np
mp
• Ab dem Zeitpunkt tU = 1 s, T U = 1010 K, haben die Neutrinos nicht mehr genügend
Energie, um den Gleichgewichtszustand zwischen Protonen und Neutronen aufrechtzuerhalten. Die Neutronen beginnen zu zerfallen. NNpn = e−1,5 ≈ 0, 22.
• Bis zu tU = 220 s: Die Neutronen zerfallen, NNnp = 0, 14. Die Energie der Photonen reicht nicht mehr aus, um die durch Nukleonenfusion erzeugten leichten Kerne
durch Photospaltung wieder zu zerlegen:
n+p→d+γ
3
3
d + n → 3H + γ
H + p → 4 He + γ
d + p → 3 He + γ
He + n → 4 He + γ
Verteilung von Helium und Wasserstoff im Universum:
Nn
m(He)
NHe
=
= 0, 081 ⇒
= 0, 25
NH
2(Np − Nn )
m(He + H + d + Li)
90
Literatur
Literatur
[1] Povh, Rith, Scholz, Zetsche: Teilchen und Kerne, Springer 2004.
[2] Mayer-Kuckuk: Kernphysik, Teubner 2002.
[3] Particle Data Booklet, Particle Data Group, online erhältlich: pdg.lbl.gov
[4] Griffiths: Introduction to Elementary Particle Physics, Wiley 1987.
[5] Demtröder: Experimentalphysik, Band 4: Kern-, Teilchen- und Astrophysik, Springer
2004.
[6] Paul, Kerne und Teilchen, Online-Skript, zu finden unter
axp01.e18.physik.tu-muenchen.de/∼skript
[7] Online-Lernsystem zur Teilchenphysik:
wswww.physik.uni-mainz.de/quast/HEP2000/TPlernen.html
[8] Perkins: Introduction to High Energy Physics, Cambridge University Press 2000.
[9] Diekmann, Heinloth: Energie, Teubner 1997.
[10] Periodensystem online: web.mit.edu/3.091/www/pt/pert1.html
Index
α-Teilchen, 6
α-Zerfall, 29, 30
Ångström (Einheit), 5
β-Zerfall, 29, 32
doppelter, 34
Fermi-Theorie, 35
γ-Zerfall, 29, 38
Äquivalenzdosis, 54
Absorber, 44
Aktivator, 61
Aktivität, 29, 54
Altersbestimmung, 41
Asymmetrieterm, 18
asymptotische Freiheit, 74
Auger-Elektron, 34
Barn (Einheit), 11
Baryonen, 69, 71
Baryonenzahl, 70
Becquerel (Einheit), 29, 54
Beschleuniger, 56
Collider, 65
Fixed Target, 65
Bethe-Bloch-Formel, 49
Bethe-Heitler-Formel, 50
Bindungsenergie, 9, 18
biologischer Wirkungsfaktor, 54
Bjorken-x, 82
Blasenkammer, 63
Bohrsches Magneton, 20
Boson, 74, 85
Bunch, 65
C-Parität, 77
C14-Methode, 41
Cabibbo-Kobayashi-Maskawa-Matrix, 87
Cerenkov-Effekt, 51
Cerenkov-Licht, 51
CMS, 64
CNO-Zyklus, 47
Collider, 65
Compton-Streuung, 52
Confinement, 74
Coulomb-Potential, 12
Coulomb-Streuung, 51
Coulombterm, 18
CP-Symmetrie, 78
CP-Verletzung, 79
CPT-Symmetrie, 80
Curie (Einheit), 54
de Broglie-Wellenlänge, 15
Deformationsparameter, 41
Detektor, 56
Deuterium, 44
Deuteron, 6
differentieller Wirkungsquerschnitt, 11
Dirac-Streuung, 16
Dosisrate, 54
Drehimpuls, 6
Driftkammer, 59
Dublett, 70
electron capture, 33
elektrische Dipolmomente, 80
elektromagnetische Wechselwirkung, 73
Elektroneneinfang, 33
Elektronenstreuung, 14
Elektronenvolt (Einheit), 5
elektroschwache Vereinigung, 87
Elemententstehung, 90
Energie, 5
Energiedosis, 54
Erhaltungssätze, 77
Experiment
allgemein, 63
HFS, 20
LHC, 64
NMR, 21
Paritätsverletzung, 37
Pound, Rebka (Photonenmasse), 40
Reimes, Cowan (Neutrinonachweis), 36
Rutherford (Streuung), 12
Superkamiokande, 64
Farbfreiheitsgrad, 72
FCNC, 87
Fermi (Einheit), 5
Fermi-Übergang, 35
Fermi-Verteilung, 18
Fermionen, 69
Fixed-Target, 65
Formfaktor, 16, 81
Fourier-Transformation, 16
freie Parameter, 89
Funkenkammer, 58
Fusionsrate, 45
Gamow-Faktor, 31
Gamow-Teller-Übergang, 35
Gasdetektoren, 57
Geiger-Müller-Zählrohr, 58
Glueball, 69
Gluon, 74, 75
Goldene Regel, 35
91
92
Gravitation, 75
Gravitationspotential, 14
Gray (Einheit), 54
Hadronen, 53, 70
Halbleiterdetektor, 60
Halbwertzeit, 29
harmonischer Oszillator, 26
Hartree-Fock-Verfahren, 26
Helizität, 15, 38
Hermaphroditen, 69
Higgs-Boson, 64, 88
Hyperfeinstruktur-Aufspaltung, 20
Hyperladung, 70
ideales Fermigas, 26
Impuls, 6
Impulsübertrag, 16
Inertialfusion, 45
innere Konversion, 38
innere Paarbildung, 38
integrierte Luminosität, 66
Ionendosis, 54
Ionisationsdetektoren, 56
Isobare, 7
Isomere, 7
Isospin, 25, 70
Isospindublett, 85
Isotone, 7
Isotope, 7
Kalorimeter
elektromagnetische, 62
hadronische, 63
Kalorimetrie, 62
Kaon, 68, 79
Kastenpotential, 26
Kernfluoreszenz, 38
Kernfusion, 44
Kernkraftwerke, 43
Kernmagneton, 20
Kernphysik, 6
Kernpotential, 14
Kernresonanz, 21
Kernspaltung, 41
spontane, 41
Kernumwandlung, 29
Kernwechselwirkung, 14
Kettenreaktion, 43
Konversionselektron, 38
Kopplungskonstante, 35, 73
kritische Masse, 44
Längeneinheiten, 5
Ladung, 6, 8, 70
Ladungsbestimmung, 8
Index
Ladungsparität, 77
Landau-Verteilung, 50
Laser-induzierte Fusion, 45
laufende Kopplung, 75
Lebensdauer, 29
Leistungsdichte, 45
Leptonen, 69
LHC, 64
Luminosität, 65
integrierte, 66
Mößbauereffekt, 39
magische Zahlen, 25
Magnetische Kernresonanz, 21
magnetisches Moment, 19
Komposition, 21
Magneton
Bohrsches, 20
Kern-, 20
Majorana-Neutrino, 34
Masse, 6
Massendefekt, 9
Massenspektrometer (Thomson), 8
Mesonen, 69, 70
Moderator, 44
Moliere-Radius, 63
Moseley-Gesetz, 8
Mott-Streuung, 15
Myon, 68
myonisches Atom, 69
Neutrino, 32
indirekter Nachweis, 33
Neutron, 9
Neutroneneinfang, 43
nukleare Absorptionslänge, 54
Nukleon, 25
Nuklide, 6
Oberflächenterm, 18
Paarerzeugung, 52
Paarungsterm, 18
Parität, 24, 77
Paritätsverletzung, 37
Partialbreite, 39
Photoeffekt, 52, 73
Photomultiplier, 61
Photon
virtuell, 73
Photospaltung, 10
Pion, 67
Planck-Skala, 5
Positronium, 69
pp-Zyklus, 47
Preon, 83
Index
Propagator, 74
Proportionalkammer, 58
Proton, 6
QCD, 74
QED, 73
QFD, 74
Quadrupolmoment, 23
Qualitätsfaktor, 54
Quantenchromodynamik, 74
Quantenelektrodynamik, 73
Quantenflavourdynamik, 74
Quantenzahlen, 70
Quarks, 69
Röntgen (Einheit), 54
rad (Einheit), 54
rem (Einheit), 54
Rutherford-Streuung, 8, 12, 73
Schalenmodell, 25
schwache Wechselwirkung, 74
Paritätsverletzung, 37
schwacher Strom, 87
Schwerpunktenergie, 65
Sekundärelektronenvervielfacher, 61
Shiva-Nova Laser, 46
Sievert (Einheit), 54
Spaltparameter, 42
Spiegelkerne, 7
Spin, 15, 70
Spin-Spin-Wechselwirkung, 16
spontante Spaltung, 41
starke Wechselwirkung, 74
Stoßfrequenz, 31
Strahlungslänge, 51
Strangeness, 68, 70
Streuung
an Ladungsverteilung, 16
Dirac, 16
Elektron-Kern, 81
Elektron-Proton, 81
Elektronen, 14
Lepton-Nukleon, 82
Mott, 15
Rutherford, 8, 12
tiefinelastische, 81
Strukturfunktion, 82
Superkamiokande, 64
Supersymmetrie, 64
Symmetrie, 77
Szintillationsdetektoren, 60
Szintillator, 60
anorganischer, 60
organischer, 60
T-Symmetrie, 80
93
Target, 11
Teilchenbeschleuniger, 56
Teilchendetektor, 56
Teilchenzoo, 67
Tevatron, 66
Tokamak, 45
Tröpfchenmodell, 18
Transformationen
diskrete, 77
kontinuierliche, 77
Transmission, 31
Triplett, 70
Tritium, 44
Triton, 6
Unitaritätsgrenze, 85
Universum, 90
Uranspaltung, 43
Vakuumpolarisation, 75
Volumenterm, 18
Wechselwirkung
elektromagnetische, 73
Gravitation, 75
schwache, 74
starke, 74
Wechselwirkungsrate, 66
Weizsäckersche Massenformel, 18
Wirkungsquerschnitt, 10
differentieller, 11
Woods-Saxon-Potential, 27
Yukawa-Potential, 67
Zählrohr, 57
Zündparameter, 45
Zeitprojektionskammer, 59
Zeitumkehr, 78
Zerfall, 29
Zerfallsbreite, 29
Zerfallskonstante, 29
Zerfallswahrscheinlichkeit, 29