1 Einleitung - G

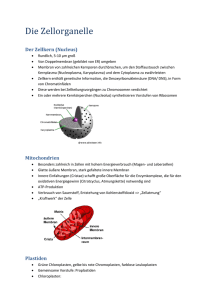
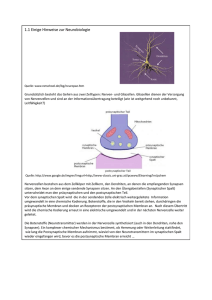
1 Einleitung
1.1 Was ist Computational Neuroscience?
1.2 Aufgaben der Computational Neuroscience
Was bedeutet Computation?
Der Aktivität unseres Gehirns liegt ein diskreter Zustand zugrunde.
Wie sind die Größen Codierung und Dynamik in der meßbaren neuronalen Aktivität
verschlüsselt? Antwort geben kann (manchmal) ein interdisziplinärer Ansatz (Computational Neuroscience):
Vereinigung von Disziplinen, wie Biologie, Medizin, Mathematik, Physik, Informatik.
1.3 Inhalt der Vorlesung
1. Biologische Grundlagen.
2. Einführung in die theoretische Neurowissenschaft.
4
a) Grundlagen.
b) Einfache Modelle (keine räumliche Auflösung.
c) Grundlagen zu räumlich aufgelösten Modellen.
3. Detaillierte Modellierung: Erfassung der räumlichen und zeitlichen Dynamik neuronaler Prozesse.
a) Einführung in die Theorie der partiellen Differentialgleichungen.
b) Numerische Diskretisierungsverfahren.
c) Lösungsverfahren für große Gleichungssysteme (vll.)
d) Bildverarbeitung und Rekonstruktionsverfahren für zelluläre Organellen.
4. Behandlung von Themen aus aktueller Forschung (Anwendung von 2. und 3.)
Notiz: Biologie und Numerik bleiben hier unvollständig! Die biologischen Grundlagen sind
jedoch ausreichend für die hier behandelten Themen. Für eine ausführliche Behandlung
der Numerik sowie Modellierung und Simulation sei auf andere Vorlesungen verwiesen.
5
2 Grundlagen der Neurobiologie
2.1 Von Genen zu Verhalten
Es existieren unterschiedliche Skalen bei der Betrachtung von Informationsverarbeitung
im Gehirn:
• Molekulare Skala (biochemische Untersuchungen)
• Zelluläre Skala (Elektrophysiologie, Einzelzellableitungen, Imagingverfahren)
• kleine Schaltkreise (s.o.)
• Netzwerke (Multielektrodensysteme)
• Areale (MRT, EEG, ...)
6
• Verhalten (Beobachtung)
Forschungsgebiete sind auf einzelne Skalen ausgerichtet, sehr schwierig zur Zeit ist die
Erfassung der Übergänge zwischen den Skalen!
2.2 Die Nervenzelle
Zelltheorie:
Ist das Gehirn ein topologisch zusammenhängendes Netzwerk, oder besteht es aus einzelnen Komponenten die miteinander kommunizieren?
Golgi-Verfahren (1885): Kalium-dichromat + Silbernitrat reagiert in der Zelle zu Silberchromat ⇒ Färbung einzelner Zellen im Netzwerk, dadurch lassen sich die elementaren
Einheiten (Zellen) darstellen.
2.2.1 Die Plasmamembran
Die Plasmamembran ist das definierende Element einer Zelle. Sie trennt den intra- und
extrazellulären Raum mit Hilfe ihrer Bilipid-Struktur.
Zusammensetzung:
55 % Proteine
25 % Phospholipide
13 % Cholesterin
4 % Lipide
3 % Kohlenhydrate
Proteine bilden den Baustein für Kanäle (passiv + aktiv) durch die selektiv definierte
Ionen zwischen Intra- und Extrazellulärraum ausgetauscht werden können (dies ist ein
wesentlicher Aspekt bei der Modellierung zellulärer Prozesse).
2.2.2 Dendriten
• Verzweigte Kabelstruktur, mit dunner werdenden Ästen je weiter man sich vom
Soma wegbewegt.
• passive Membraneigenschaften (Signaldämpfung während Signalausbreitung).
• Empfänger für Signale anderer Zellen.
• Weiterleitung elektrischer Signale zum Soma und Axon.
7
2.2.3 Axon
• Ähnliche Struktur wie Dendriten, kleinere Kabeldurchmesser.
• aktive Membraneigenschaft (keine Signaldämpfung)
• Myelinumhüllung ⇒ schnellere Signalgeschwindigkeit.
• Signalweiterleitung an verbundene Zellen.
2.2.4 Soma
• beherbergt den Zellkern, Endoplasmatisches Retikulum und andere Organellen
(Mitochondrien, Golgi-Apparat, ...)
• größter Teil des zellulären Volumens.
• verbindet Dendriten und Axon.
• gefüllt mit Zytosol.
2.2.5 Zellkern
• befindet sich im Soma der Zelle.
• im Zellkern ist die DNA aufgewickelt.
• durch Kernporen in der Doppel-bilipidmembran können Ionen diffundieren welche,
für die Zelle überlebenswichtige, biochemische Prozesse aktivieren können (z.B.
Kalzium).
• im Zellkern wird zusammen mit dem Endoplasmatischen Retikulum die DNA in
Proteine umgewandelt (Membranaufbau, Kanäle, Rezeptoren etc.) → Plastizität.
2.2.6 Endoplasmatisches Retikulum (ER)
• äußere Membran des Zellkerns erstreckt sich in das ER.
• Rauhes ER: Synthese von Proteinen.
• Glattes ER: Produktion bestimmter Lipide, Fettsäuren und Aufnahme von Kalzium.
• großer Kalziumspeicher: ER-Membran ermöglicht Austausch von Kalzium zwischen
Zytosol und ER (SERCA, IP3-R, RyR) → CICR.
• erstreckt sich weit in die Dendriten.
8
2.2.7 Mitochondrien
• Energieversorgung: über stark gefaltete innere Membran wird ein Protonengradient
aufgebaut. Darüber wird ATP-Produktion angetrieben (z.B. Zitronensäurezyklus).
• Kalziumspeicher.
2.2.8 Das Zytoskelett
Das Zytoskelett ist das Transportnetz der Zelle. Es besteht aus dynamischen Filamenten.
Eindimensionale Strukturen: Mikrotubuli
• 20nm Durchmesser.
• Motorproteine bewegen Moleküle und Organellen entlang von Mikrotubuli.
Zweidimensionale Strukturen: Aktin und Neurofilamente
Polymerisation von Aktin erzeugt eine 2D-Matrix welche in der Regel mit der Zellmembran verbunden ist (Formstabilität der Zelle).
Neurofilamente
1. bilden die Kernlamina (im Zellkern).
2. betten die DNA ein.
3. stabilisieren die Kernmorphologie.
Dreidimensionale Strukturen
Verbindungen zwischen 1D- und 2D-Zytoskelettbausteinen liefert der Zelle eine dreidimensionale Infrastruktur für den Transport von Molekülen und Organellen.
2.3 Verbindungen zwischen Nervenzellen
Wie sind Nervenzellen miteinander verbunden? Oder zuerst: Wann können Nervenzellen
eine Verbindung eingehen?
Rückblick: Axon leitet Signal weiter, Dendriten empfangen ⇒ Axon und Dendriten
müssen in Kontakt treten, räumliches Kriterium.
9
2.3.1 Gap Junctions
In Bereichen in denen Nervenbahnen dicht und parallel verlaufen können sich bei einem
Abstand von 2-4nm Gap Junctions ausbilden.
Gap Junction:
• Gap Junctions sind Proteinkomplexe welche transzellulären Ionenaustausch ermöglichen.
• sehr schnelle Signalübertragung.
• geringe Selektivität bei der Signalübertragung.
Q: Warum nimmt die Dichte der Gap Junctions bei höheren Lebewesen ab?
A: geringe Selektivität: GJ-gekoppelte Zellen leiten Signal immer weiter ⇒ Komplexitätsreduktion!
Erhöhung der Komplexität → chemische Synapsen.
2.3.2 Chemische Synapsen
Komplexere Signalweiterleitung als bei Gap Junctions.
Typeinteilung: nach Art des Neurotransmitters, grob: hemmende oder erregende Synapsen.
Präsynapse
• Neurotransmitter gelangt über das Axon oder die präsynaptische Membran in den
präsynaptischen Bouton.
• Umsetzung an der Vesikeloberfläche zu spezifischem Neurotransmitter und Befüllung der Vesikel.
• Vesikel wandern zu präsynaptischer Membran.
Exozytose
Fusion der Vesikelmembran mit präsynaptischer Membran.
Aktionspotential → Änderung der Membranspannung → Öffnung von Kalziukanälen
→ Kalziumeinstrom → Fusion.
Endozytose
Massenerhaltung bei Vesikeln, d.h. nach Exozytose müssen neue Vesikel entstehen. Dieser
Prozess wird als Endozytose bezeichnet.
Endozytose: Aus der fusionierten Membran (alle Proteinkomplexe vorhanden) wird
neben der active zone Membran abgeschnürt um neue, leere, Vesikel zu bauen. Diese
werden anschließend befüllt.
10
Signalübertragung durch den synaptischen Spalt
• freigesetzter Neurotransmitter diffundiert zur postsynaptischen Membran.
• Aktivierung postsynaptischer Rezeptoren.
• Öffnung ionenspezifischer Kanäle.
• Änderung der Membranspannung.
• Signalweiterleitung in postsynaptischer Zelle.
2.4 Aufbau der Großhirnrinde
Grobe Einteilung in
1. primäre und sekundäre sensorische Kortexareale.
2. primäre und sekundäre motorische Kortexareale.
3. Assoziationskortizes (Sprache, Informationsverarbeitung...)
In die Tiefe: schichtweise Anordnung der Zellen. Schichten werden nach dem Zelltyp
benannt, der sich dort befindet.
Häufigster Zelltyp: Pyramidenzellen (80%).
Häufig untersuchte Gehirnregion:
Hippocampus
1. Maßgeblich beteiligt bei Lernen und Gedächtnis.
2. sehr planare Struktur, d.h. experimentell sehr gut zugänglich.
2.5 Elektrische Eigenschaften von Neuronen
Ionenkanäle in der Plasmamembran sorgen für den Austausch spezifischer Ionen. Der
Austausch erfolgt entlang von Konzentrations- und Spannungsgradienten. Ionenpumpen
arbeiten entgegen des Gesamtgradienten (Energieverbrauch).
Kationen
K+
Na+
Ca2+
Mg2+
Kationen total
Innen [mM]
124
10
5
14
153
Außen [mM]
2
125
2
1
130
11
Anionen
Cl−
HCO−
3
Andere
Innen [mM]
2
12
139
Außen [mM]
77
27
26
Anionen total
153
130
2.5.1 Membranpotential, Membrankapazität und Membranwiderstand
Membranpotential
An der Plasmamembran baut sich eine Potentialdifferenz zwischen Intra- und extrazellulärem Raum auf, das Membranpotential. Außenraum wird per Konvention auf 0 gesetzt.
Membranpotential variiert im Ort ⇒ Zellen sind nicht isopotential. ⇒ Ionenfluss durch
die Zelle entlang des Potentialgradienten.
Satz 1. Sei IL der axiale Ionenfluss, RL der axiale Widerstand und rL der intrazelluläre
Widerstand eines Zylinders mit der Länge L und Basisfläche a. Bei x = 0 liegt die
Spannung V1 an, bei x = L Spannung V2 . Dann gilt:
V 2 − V1
RL
L
= rL 2
πa
IL =
RL
(2.1)
(2.2)
Elektrotonische Eigenschaften werden durch die Form der Zelle beeinflusst.
Q: Wie wirkt sich die Änderung des Membranpotentials in Zelle A und B aus?
A: Morphologisch kompakte Zellen sind auch elektrotonisch kompakt. Zelle B kann daher
näherungsweise als isopotential angenommen werden.
⇒ Einfachstes Modell: Zelle wird als eine Einheit modelliert.
Membrankapazität
Die Membran kann als Kondensator interpretiert werden.
Satz 2. Sei Cm die Membrankapazität, Q die Ladungsdifferenz und Vm die Membranspannung, dann gilt
Q = Cm Vm
12
(2.3)
Cm ist dabei proportional zur Zelloberfläche A.
Definition 1. Mit cm wird die spezifische Membrankapazität bezeichnet:
cm :=
Cm
A
(2.4)
Diese liegt typischerweise bei cm = 10nF/mm2 .
Membranwiderstand
Wenn eine Zelle aktiv ist, bedeutet dies ihr Membranpotential befindet sich nicht im
Ruhepotential, d.h. um sich aus dem Ruhezustand zu bewegen muss der Membranwiderstand überwunden werden.
Ohm’sches Gesetz:
∆V
(2.5)
Ie
Ie sei dabei der Strom der von einer Elektrode e injiziert wird, ∆V die Potentialdifferenz.
Bei Nervenzellen liegt der Membranwiderstand typischerweise im Bereich 10 − 100M Ω.
Rm =
Definition 2. Spezifische Größen:
rm : spezifischer Widerstand.
τm : Membran-Zeitkonste.
Die Membranzeitkonstante τm ist definiert als
τm := rm cm
2.5.2 Ionengleichgewichte
An der Plasmamembran herrscht ein Konzentrationsgradient sowie ein elektrischer Gradient. Befinden sich die gradientenabhängigen Austauschprozesse im Gleichgewicht, dann
ist der Netto Ionenfluss Null.
Berechnung des Ruhepotentials:
An der Membran existiert eine Potentialsprung (Vm = Vi −Va ), d.h. eine Energiebarriere.
Satz 3. Ein Teilchen mit Ladung z · q benötigt eine Energie E von mindestens
mit
z: Teilchenladung
q: Protonenladung
zur Überquerung der Membran.
E ≥ −zqV
13
(2.6)
Die Wahrscheinlichkeit dafür berechnet sich aus der Bolzmann-Verteilung der Wahrscheinlichkeitsdichten:
Satz 4. Sei T die absolute Temperatur und kb die Bolzmann-Konstante. Dann gilt:
P (E ≥ −zqV ) = exp(−zqV /kb T )
(2.7)
Definition 3. Sei R die allg. Gaskonstante und F die Faraday-Konstante. Die thermische Energie von 1 mol Ionen sei definiert als die Energie die benötigt wird um 1 mol
Ionen über die Membran zu transportieren:
�
�
R·T
kb T
VT ≡
=
(2.8)
F
q
Im Gleichgewicht gilt:
V = Vgg
(2.9)
⇒P (E ≥ −zqV ) = exp(zVgg /VT )
⇒[außen] = [innen] exp(zVgg /VT )
�
�
VT
[außen]
⇔Vgg =
ln
(N ernst − Gleichung)
z
[innen]
2.5.3 Goldman-Hodgkin-Katz Gleichung
Die Nernst-Gleichung berechnet das Ruhepotential bei Beteiligung eines Ionentyps.
Problem: Unterschiedliche Kanäle, verschiedene Ionentypen
⇒ GHK-Gleichung
Umkehrpotential Em =
 �n
PK + [Ki+ ]A +
�m
PA− [A−
j ]I

i=1
j=1
RT
i
j

ln  �n
�m
+
−
F
i=1 PK + [Ki ]I +
j=1 PA− [Aj ]A
i
j
(2.10)
Herleitung (angedeutet):
• Membran ionenpermeabel
• Ionen können per Diffusion (Fick’sches Gesetz) und per elektrischem Fluss
(beeinflusst vom elektrischem Feld) die Membran passieren
Gesamtionenfluss jIon :
�
�
d [Ion] nIon F Em
(∗) jIon = −DIon
−
·
[Ion]
(2.11)
dz
RT
L
n : V alenz
L : M embrandicke
14
Herleitung der GHK-Gleichung (ausführlich):
 �n

�m
+
−
P
+
P
+ [K ]
− [A ]
i=1
j=1
i
j
K
A
a
RT
i
i
j

Em =
ln  �n
�m
+
−
F
i=1 PK + [Ki ]i +
j=1 PA− [Aj ]a
i
(2.12)
j
2 Kräfte wirken auf Ionen:
1. Diffusion (Fick’sches Gesetz)
2. elektrischer Fluss (definiert durch elektrisches Feld)
Ionen, die die Membran passieren, folgen dem Gesamtfluss
�
�
d [Ion] nIon F Em
(∗) jIon = −DIon
−
·
[Ion]
dz
RT
L
(2.13)
n : V alenz
L : M embrandicke
Dies definiert ein 1-dimensionales Problem senkrecht zur Membran.
Lösung: Variablentrennung (z, [I]):
jI − DI ·
nI F Em
d [I]
·
[I] = −DI ·
RT
L
dz
⇔
Integration über Membran:
�
L
0
⇒L =
dz =
�
�
�
1
Ω[I]
ln −
− DjII
−
dz =
d [I]
− DjII
−
nI F
RT
·
Em
L
[I]
(2.14)
d[I]
(2.15)
[I]
�
�
�� �
�
jI
nI F E m
RT L
[I]a − ln −
−
[I]i
· −
DI
RT L
nI F Em
nI F Em
RT L
jI
nI F E m
−
DI
RT L
nI F E m
= ln (. . . [I]a ) − ln (. . . [I]i )
RT
� j
�
F Em
− DII − nIRT
[I]
nI F Em
a
L
⇔ e RT = −
F Em
− DjII − nIRT
[I]
i
L
⇔−
F Em
Sei µ definiert als µ :=
.
�
�RT
jI
nI
jI
nI
⇔ enI µ −
− µ [I]i = −
− µ [I]a
DI
L
DI
L
· nI µ ([I]i · enI µ − [I]a )
(1 − eni µ )
[I]a − [I]i · enI µ
⇐⇒
j
=
P
·
n
µ
·
I
I
I
D
(1 − eni µ )
PI = I
L
D
⇔ jI = − L
Definition 4. Sei die Stromdichte definiert durch JI := qA jA . Dabei bezeichnet qA die
Ladung.
15
Man betrachte den Gleichgewichtszustand Jges ≡ 0
⇒ Jges =
�
JI = 0
I
und den Fall nI = ±1 (Monovalenz, z.B. Na+ , K+ , Cl− ):
(u :=)


�
PKi [Ki+ ]a +
i
�
j

·
PAj [A−
j ]i


µ
�
�
· e ·µ
=
PKi [Ki+ ]i +
PAj [A−
]
j a
1 − eµ
i
µ
1 − eµ
(2.16)
(=: v)
j
u
⇔e =
v
u
⇔ µ = ln
v ��
�
�
PKi [Ki+ ]a + PAj [A−
]
F Em
j i
⇔
= ln �
�
RT
( PKi [Ki+ ]i + PAj [A−
j ]
µ
a
⇔Em
RT
=
ln(. . . )
F
Gleichung (∗) kann eindimensional in z geschrieben werden (z ⊥ Membran), wenn Rest
rotationssymmetrisch ist (Kabel).
⇒ Löse (∗) analytisch.
Beispiele:
1. Na+ , K+ , Cl−
Vm
RT
=
ln
F
�
PN a+ [N a+ ]A + PK + [K + ]A + PCl− [Cl− ]I
PN a+ [N a+ ]I + PK + [K + ]I + PCl− [Cl− ]A
�
(2.17)
2. Na+
Vm =
RT
ln
F
�
PN a+ [N a+ ]A
PN a+ [N a+ ]I
⇒ Nernst-Gleichung
16
�
=
RT
ln
F
�
[N a+ ]A
[N a+ ]I
�
(2.18)
2.5.4 Membranstrom
Definition 5. Als Membranstrom bezeichnet man den Gesamtladungsfluss über die Plasmamembran
Konvention: positiver Strom, wenn positive Ladungen von Extra- zu Interzellulärraum
wandern; negativer Strom, wenn andersherum.
Definition 6. Folgende Größen finden häufig Verwendung:
V − Ei
im =
�
i
gi
gi (V − Ei )
driving f orce f ür Ion i
Leitf ähigkeit (pro F läche)
M embranstrom
2.5.5 Experimenteller Ansatz
17
2.5.6 Messungen des Ruhepotentials
Experimentelle Ermittlung der Umkehrpotentiale im Vergleich zu Nernst- und GHKWerten.
Nernstgleichung liefert für kleine Na+ schlechte Werte.
EN a = +55 mV
EK = −75 mV
18
GHK für Na+ und K+ : Vm ≈ −60mV
PN a+ ≈
1
25
· PK +
2.5.7 Ein äquivalenter Schaltkreis
2.5.8 Das Aktionspotential
Beobachtung (Cole & Curtis 1939):
Q: Was bewirkt eine Depolarisierung bis 50 mV ?
• Änderung der Gesamtpermeabilität? Nein, da bei völliger Durchlässigkeit nur bis
0 mV.
• Na-Kanäle (Nernst ⇒ EN a+ ≈ 55 mV )
Experimentelle Untersuchung:
19
• Änderung der extrazellulären Na+ -Konzentration ⇒ Änderung der Amplitude (keine Änderung im Ruhepotential)
Erklärung von Cole & Curtis:
• Änderung in der Membranspannung bewirkt Änderung in der Na+ -Leitfähigkeit.
(Elektrochemischer Gradient von Na+ bewirkt Einstrom von Na+ -Ionen)
• Na+ -Ionenkanäle sind spannungsabhängig (Spannungssensor im Proteinkomplex)
2.5.9 Hodgkin-Huxley-Formalismus
Angestrebt wird ein Wechsel von der Beschreibung der Einkanaldynamik zur Beschreibung einer makroskopischen Kanaldynamik und die Beobachtung der zeitlichen Änderung von Leitfähigkeit und Ladungsfluss durch die Membran.
Experimenteller Ansatz:
Festsetzen des Membranpotentials auf unterschiedlichen Werten.
Exp 1: Depolarisierung um 60 mV in Tintenfisch-Axon
(a) unter normalen Bedingungen
(b) ohne Na+ -Ionen
(c) berechneter Na+ -Beitrag
Exp 2: Vm = 60 − 150 mV
(a)
(b) + TTX: Ausschalten der Na+ -Kanäle
(c) + TEA: Ausschalten der K+ -Kanäle
Interpretation:
K+ :
• Mit zunehmendem Vm nimmt die Leitfähigkeit der K+ -Kanäle zu.
• später ”on-set”
Na+ :
• Vm ↑ ⇒ Na+ -Leitfähigkeit ⇒
rung + Inaktivierung).
Vm ↑↑ ⇒ Leitfähigkeit ↓ (Na+ -Kanal Aktivie-
• früher ”on-set”
20
Das Aktionspotential:
Das Aktionspotential wird im Wesentlichen bestimmt von Na+ -Kanal Aktivierung +
Inaktivierung sowie K+ -Kanalaktivität.
⇒ Hodgkin-Huxley-Modell (später)
Unterschiede am Axon:
1. unmyeliniertes Axon
2. myeliniertes Axon
21