Arbeit und Leistung

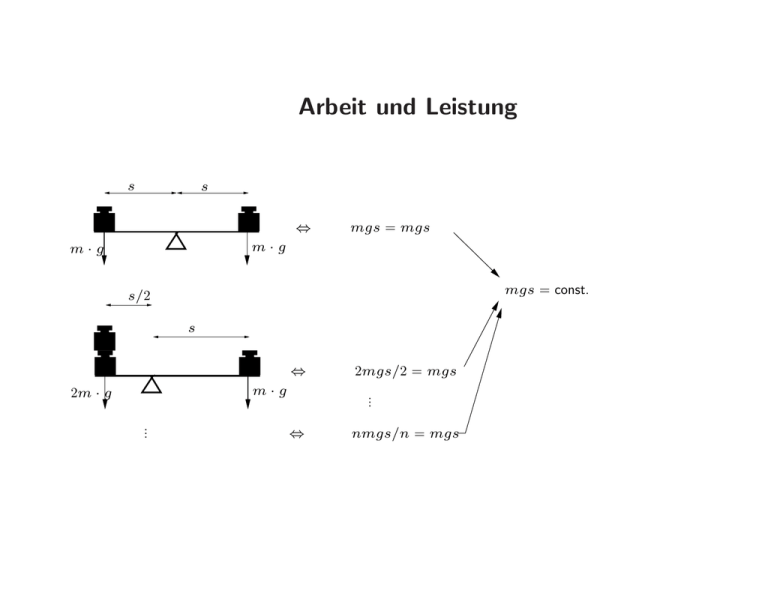
Arbeit und Leistung
s
s
m·g
m·g
⇔
mgs = mgs
mgs = const.
s/2
s
m·g
2m · g
..
.
⇔
2mgs/2 = mgs
⇔
nmgs/n = mgs
..
.
Arbeit und Leistung
Arbeit ist Kraft mal Weg
•
•
•
•
Gotthardstraße
Treppe und Lift
Feder
Bergsteiger/Wanderer
Arbeit und Leistung
F~Zug
F~tot = F~Zug − F~k
F~k
h
s
m·g
l = s cos α
α
Gleichmässige Bewegung:
F~zug = −F~k
Fk = m · g · sin α
A = Fk · s ; s = sinhα
A = mgsinsinααh = mgh
Arbeit und Leistung
Wunder ist
kein Wunder
Simon Stevin,
um 1600
Arbeit und Leistung
E=
R
d~s · F~ =
R
ds F cos α
F~
α
d~s
Arbeit und Leistung
Arbeit ist Kraft mal Weg [Arbeit] = N m = J = W s
Leistung = Arbeit pro Zeit [Leistung] = N m/s = J/s = W
Beispiel:
100 kg Backsteine 10 m hochtragen.
E = mgh = 100 · 9, 81 · 10 kg m2/s2 = 9810 J = 2, 725 Wh
dito innerhalb von 10 Minuten: Leistung P = 9810/600 J/s = 16, 35 W.
Potentielle und kinetische Energie
• Energie: gespeicherte, “mögliche” (potentielle) Arbeit
• potentielle Energie: Lageenergie (Wasser im Stausee,. . . )
• kinetische Energie: Bewegungsenergie
Epot = mgh −→ vh =
p
vh2
mgvh2
m 2
2gh −→ h =
=⇒ mgh =
= vh = Ekin
2g
2g
2
Energieerhaltung
Energie bleibt erhalten bzw. wird umgewandelt, d. h. E = Epot + Ekin = const.
Beispiele:
• Pendel
• Galilei’sches Hemmungspendel
Formal:
Z
dv
m 2
E = dx ma = m dx = m v dv = v .
dt
2
Umwandlung von potentieller in kinetische Energie. Oft wird Energie auch in
andere Formen umgewandelt, wie Wärme, Schall, Deformation, etc.
Z
Z
Bewegung in Systemen mit mehreren Massenpunkten
Wir betrachten ein System mit mehreren Massenpunkten. Für jeden Massenpunkt
i einzeln gilt nach Newton 2:
d~
pi
Fi =
.
dt
Für n Massenpunkte muss also ein System von n Bewegungsgleichungen gelöst
werden. Vereinfachend beginnen wir mit n = 2.
d~
p1
F~1 + F~21 =
,
dt
d~
p2
~
~
,
F2 + F12 =
dt
wobei F~21 die Kraft darstellt, welche Massenpunkt 2 auf Massenpunkt 1 ausübt.
F~1 stellt die Kraft dar, welche von außen auf Massenpunkt 1 wirkt. Die Kräfte
können z. B. vom Ort oder der Geschwindigkeit abhängen. Nach Newton 3 ist
F~21 = −F~12. Damit fallen die “inneren” Kräfte beim Bilden der Summe der
Bewegungsgleichungen heraus:
p2 d~
p
d~
p1 d~
+
= .
F~ = F~1 + F~2 =
dt
dt
dt
Ist F~ = 0, so ist
d~
p
= 0, bzw. p~ = const.,
dt
analog zum zweiten Newtonschen Gesetz.
Ohne Einwirkung äußerer Kräfte (F~ = 0) bleibt in einem System von n
p
Massenpunkten der Gesamtimpuls erhalten ( d~
dt = 0).
Impuls und Impulserhaltung
~v1 = ~v2 = ~0
~u1
m1
m2
~u2
Danach muss gelten
m1u1 + m2u2 = 0,
woraus sofort folgt, dass
m1
u1 .
m2
Beispiel: Rakete, hier verändert sich allerdings m mit der Zeit. . .
u2 = −
Impuls und Impulserhaltung
Anwendung: Ballistisches Pendel
α
√
u2 = 2g ∆h
mv1 = (m + M )u2
v1 = . . . Übung!
l
∆h
v1
m
M
M +m
u2
Frage: Wie groß ist der Anteil der Energie, der in Wärme und Deformation umgewandelt wird?
Stöße
Man unterscheidet verschiedene Sorten von Stößen:
• inelastischer Stoß: endotherm, Umwandlung kinetischer Energie in innere
Energie (z. B. Wärme)
• elastischer Stoß: Energieerhaltung
• schiefer Stoß: Geometrieeffekte
• (exothermer Stoß: Umwandlung innerer Energie in kinetische Energie
(z. B. e− − e+ −→ 2γ))
Inelastische Stöße
u1
v1
u2
v2
teilweise inelastisch
v1
v2
u
vollständig inelastisch
Inelastische Stöße II
Vollständig inelastischer Stoß:
m1v1 + m2v2 = (m1 + m2)u,
m1v1 + m2v2
also u =
.
(m1 + m2)
Vorzeichen von v1 und v2 beachten! Für m1 = m2 gilt offensichtlich
u=
v1 + v2
.
2
Aus den Geschwindigkeiten lässt sich die in innere Energie verwandelte kinetische
Energie berechnen (Übung!).
Elastische Stöße
Zusätzlich bleibt kinetische Energie erhalten!
1
1
1
1
2
2
2
m1v1 + m2v2 =
m1u1 + m2u22,
2
2
2
2
m1v1 + m2v2 = m1u1 + m2u2.
Zwei Unbekannte, zwei Gleichungen! Sortiere nach Körpern 1 und 2:
1
1
2
2
2
2
m1 v1 − u1 =
m2 u2 − v2 ,
2
2
m1 (v1 − u1) = m2 (u2 − v2) .
Dividiere Gleichung 1 durch Gleichung 2 und löse nach u1 und u2 auf.
(1)
(2)
Elastische Stöße
u1 =
u2 =
2m2
m1 − m2
v1 +
v2
m1 + m2
m1 + m2
m2 − m1
2m1
v2 +
v1
m1 + m2
m1 + m2
Spezialfälle:
• m1 = m2 =⇒ u1 = v2 und u2 = v1
• m1 ≫ m2 =⇒ u1 ≈ v1 und u2 ≈ 2v1 − v2
(3)
(4)
Stoß mit einer unbeweglichen Wand
m1 , u1
m1, v1
m2 = ∞
v2 = 0
u2 = 0
Mehrere Körper auf einer Linie
v1
m1
n1m1v1 = n2m2v2 (Impulssatz);
v2
m2
n
n2
n1
m1v12 = m2v22 (Energiesatz).
2
2
m1 = m2 =⇒ n1 = n2
Bewegung in der Ebene
v2,y
v1,x
y
v2,x
v1,y v
1
x
v2
α
α
Überlagerung einer Bewegung entlang von x mit einer Reflexion an einer Wand.
v2,x = v1,x; v2,y = −v1,y
m2 6= ∞
Wie soll nun ein Stoß in der Ebene behandelt werden, wenn m2 6= ∞? Aus der
Impuls- und Energieerhaltung
m1~v1 + m2~v2 = m1~u1 + m2~u2,
1
1
1
1
2
2
2
m1v1 + m2v2 =
m1u1 + m2u22
2
2
2
2
ergeben sich nur drei Bedingungen an die vier Unbekannten u1,x, u1,y , u2,x und
u2,y . Offensichtlich wird die Situation in drei Dimensionen noch schlimmer,
6 Unbekannten stehen nur vier Gleichungen gegenüber. Diese prinzipielle
Schwierigkeit lässt sich nicht beheben, wohl aber in handlichere Teilprobleme
unterteilen.
Der Schwerpunkt eines Systems
m1
~r1
z
m2
~r2
m3
~rS
~r3
y
x
N
X
m
~
r
1
.
i i
mi~ri
~rS = Pi=1
=
N
M
i=1 mi
i=1
PN
Schwerpunktgeschwindigkeit
Greifen keine äußeren Kräfte an, so bleibt der Impuls des Systems konstant.
N
X
d~
pi
i=1
dt
= 0.
Verändern sich die Massen nicht, so ändert sich auch die Geschwindigkeit des
Systems nicht, genauer,
N
X
d~vi
= 0.
mi
dt
i=1
Damit lässt sich eine mittlere Geschwindigkeit definieren, welche unverändert
bleibt:
Offensichtlich ist
N
. 1 X
~vS =
mi~vi.
M i=1
d~rS
,
dt
d. h. die Geschwindigkeit des Schwerpunktes des Systems bleibt erhalten.
Oft vereinfachen sich die auftretenden Gleichungen erheblich, wenn man in das
Schwerpunktsystem transformiert, denn
~vS =
p~S
=
N
X
mi~vi = M~vS
i=1
p~S,S
=
N
X
i=1
mi (~vi − ~vS ) =
N
X
i=1
mi~vi −
N
X
i=1
mi~vS = M~vS − M~vS = ~0.
Die kinetische Energie transformiert sich ebenso einfach:
Ekin =
=
=
=
Ekin =
1
1
2
m1v1 + m2v22
2
2
1
2
2
m1(~v1,S + ~vS ) + m2(~v2,S + ~vS )
2
1
1
2
2
2
2
m1v1,S + m2v2,S + m1vS + m2vS + (m1~v1,S + m2~v2,S ) · ~vS
2
2
1
1
2
2
2
2
m1v1,S + m2v2,S + m1vS + m2vS + 0
2
2
1
(S)
Ekin + M vS2
2
weil ja (m1~vS + m2~vS ) = ~0.
Bewegung zweier Teilchen im Schwerpunktsystem
Nach Voraussetzung wirken keine äußeren Kräfte auf das System, d. h. es wirken
nur die inneren Kräfte F~12 und F~21.
d~v1,S
F~21
;
=
dt
m1
d~v2,S
F~12
=
dt
m2
Subtraktion (unter Berücksichtigung von F~12 = −F~21) liefert
d(~v1,S − ~v2,S )
=
dt
1
1
+
F~21,
m1 m2
wo (~v1,S − ~v2,S ) = ~v12,S die Relativgeschwindigkeit zwischen den Teilchen
darstellt. Mit der Definition der reduzierten Masse µ
. m1 m2
µ=
m1 + m2
kann so eine besonders einfache Bewegungsgleichung gefunden werden
dv12,S
.
F~21 = µ
dt
Die Bewegung der beiden Teilchen kann also auf die Bewegung eines einzelnen
Teilchens der reduzierten Masse µ reduziert werden.
Elastische Stöße im Schwerpunktsystem
Wegen p~S,S = ~0 muss auch gelten
p~1,S = −~
p2,S
und p~′1,S = −~
p′2,S .
Einsetzen in den Energiesatz ergibt
1 1
1 1
1
1
=
+
p′2
+
p21,S + Q.
1,S
2 m1 m2
2 m1 m2
Verwende reduzierte Masse µ, so
p21,S
p′2
1,S
=
+ Q.
2µ
2µ
2
Für elastische Stöße ist Q = 0 (nach Definition), folglich p′2
1,S = p1,S und
2
p′2
2,S = p2,S .
Dies lässt lediglich eine Drehung der Impulse zu!
~v1′
~v2,S
~v2
~v1′ ,S
θ
~v2′
Laborsystem
~v1,S
~v2′ ,S
~v1
Schwerpunktsystem
Relativistische Formulierung
y
K
~
vA
~
uA
A
u=0
x
B
~
vB
y′
~
uB
K′
~
vA
u = vxA
~
uA
A
B
~
uB
~
vB
x′
Wir betrachten nun zwei Körper derselben Masse mA =
mB = m, die sich bei relativistischen Geschwindigkeien
begegnen. Wie sieht ein Stoß in diesem Falle aus? Dabei
bewegen wir uns in einem System K so, dass sich der
Körper A in y Richtung nur sehr langsam bewegt und
diese Impulskomponente beim Stoß umgekehrt wird,
vyA = −uyA. Dasselbe geschehe mit Körper B und
Körper A bewege sich immer noch mit Geschwindigkeit
vxA in x-Richtung. Der Impuls ist also erhalten.
Nun betrachten wir den Stoß im System K ′, welches
sich mit v = vxA entlang der x-Achse bewegt. In diesem
System sind also die Rollen von A und B vertauscht.
Die Geschwindigkeiten transformieren sich gemäß der
Lorentz-Transformation,
vy′
vy /γ
.
=
1 − vxv/c2
Nun ist im System K für die beiden Teilchen die Geschwindigkeit in x-Richtung
verschieden, weshalb sich auch die y-Komponenten der Geschwindigkeit anders
transformieren!
′
=
vyA
vyA/γ
vyA/γ
=
= γvyA,
2
2
2
1 − vxAv/c
1 − v /c
′
vyB
vyB /γ
= vyB /γ,
2
1 − vxB v/c
=
da v = vxA,
da vxB = 0,
während die entsprechenden Geschwindigkeiten im System K die Beträge |vyA|
und |vyB | haben, also
′
′
vyB
vyA
1
= γ und
= .
vyA
vyB
γ
In beiden Systemen gilt der Impulssatz. Weil beide System K und K ′ so gewählt
sind, dass beide Körper die y-Komponente ihres Impulses umdrehen, gilt
′
′
.
+ m′B vyB
mAvyA + mB vyB = 0 = m′AvyA
Dies ist aber für mA = m′A und mB = m′B nicht möglich, weil ja die yKomponenten der Geschwindigkeiten verschieden sind. Also müssen die Massen
m und m′ verschieden sein! Für kleine y-Komponenten gilt die Näherung
vA ≈ vxA = v
VB ≈ 0
′
, vA
≈ 0,
′
≈ vxB = v.
, vB
.
Damit können wir mit m0 = m(v = 0) schreiben
m(v)vyA + m0vyB
= 0,
′
m0vyA
+ m(v)vy′ B
= 0.
′
Wir nehmen die Terme mit vyB bzw. vyB
nach rechts, dividieren die Gleichungen
und erhalten
′
m2(v) vyB vyA
2
=
γ
.
=
′ v
m20
vyB
yA
m0
Damit erhalten wir
.
m(v) = γm0 = p
2
2
1 − v /c
Relativistische Energie: E = mc2
Wir wollen nun noch die bekannt EnergieMasse Beziehung E = mc2 verstehen. Dazu
E
betrachten wir einen leichten Wagen, an
Schwerdessen linker Wand ein Lichtblitz der Energie
Lichtblitz punkt
E ausgesandt wird. Nach den Gesetzen der
klassischen Physik hat er einen Impuls p =
∆x
E/c (Stoff kommt im zweiten Semester). Weil
E
der Wagen vor dem Blitz ruhen soll, muss
auch nach dem Blitz der Schwerpunkt am
selben Ort bleiben, der Gesamtimpuls bleibt
erhalten. Deshalb muss sich der Wagen ein
klein wenig nach links bewegen mit einer Geschwindigkeit v = −p/M = −E/M c.
Weil diese Geschwindigkeit sehr klein ist im Vergleich zur Lichtgeschwindigkeit,
L
v ≪ c, erreicht der Lichtblitz die rechte Wand nach einer Zeit ∆t = L/c,
während der sich der Wagen lediglich um ∆x = v∆t = −EL/M c2 nach links
bewegt hat. Erreicht der Blitz die rechte Wand, so hält der Wagen an. Damit
der Schwerpunkt unbewegt bleibt, muss dem Licht eine Masse m zugeschrieben
werden!
mL + M ∆x = 0.
Daraus folgt
mL − M EL/M c2 = 0,
=⇒
E = mc2.
Setzen wir darin nun unseren Ausdruck für die Masse ein, so finden wir
m0c2
E=p
= m0c2 − (m(v) − m0)c2,
1 − v 2/c2
wobei der erste Term dies sog. Ruheenergie und der zweite die eigentliche
kinetische Energie ist. Für diese gilt mit einer Potenzreihenentwicklung für γ
Ekin
4
1
3
v
= (m(v) − m0) c2 = m0v 2 + m0 2 + . . .
2
8 c
Für kleine Geschwindigkeiten v ≪ c finden wir den klassischen Ausdruck wieder.
Für richtige Rechnungen ist es oft nützlicher, die Energie-Impuls Beziehung zu
kennen:
q
E = c m20c2 + p2.
Relativistische Kraft
Wir nehmen den relativistischen Impuls p = γm0v und das zweite Newtonsche
Gesetz und erhalten
F~
=
=
d
d
m0~v
d~
p
p
= (m~v ) =
dt
dt
dt
1 − v 2/c2
!
d
m0
p
~v + m~a.
dt 1 − v 2/c2
!
,
Die innere Ableitung in der Klammer wird mit d/dt = (dv/dt)(d/dv) durch-
geführt:
F~
2
=
m0 v/c
(1 −
a
3/2
v 2/c2)
2
~v + m~a,
2
v ~v
v ~a
3
= γ m0 a 2 + 1 − 2
.
c v
c a
Die Kraft hat also nicht nur eine Komponente in Beschleunigungsrichtung
~a/a, sondern auch in Geschwindigkeitsrichtung ~v /v! Diese wird aber für kleine
Geschwindigkeiten v ≪ c vernachläßigbar.