VL9

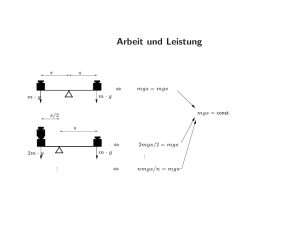
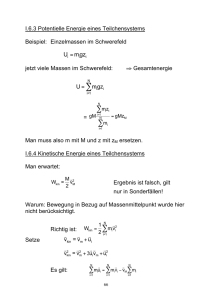
Mechanik II /Vorlesung 9 / Prof. Popov
Beispiele für Energieerhaltung, Impulserhaltung.
Literatur: Hauger, Schnell und Groß. Technische Mechanik III, 1.2.7, 2.5
I. Beispiele
B1. Schleifenfahrt (Looping)
Ein Körper gleitet von einer Höhe h mit der
Anfangsgeschwindigkeit v0 = 0 eine schiefe
Ebene hinab, die in einer Kreisschleife ausläuft. Es soll diejenige Höhe bestimmt werden,
für die kein Ablösen von der Kreisbahn mit
dem Radius R eintritt.
Bedingung
dafür ist, daß
der Bahndruck
im höchsten
Punkt P der
Kreisbahn
verschwindet,
d.h.
2
v
m 2 = mg .
R
Eine Energiebilanz zwischen dem Anfangspunkt und dem höchsten Punkt in der Schleife
liefert:
v2
0 + mgh = 2mgR + m 2
2
Daraus folgt die Höhe h = ( 5 / 2 ) R .
B2. Ein Fadenpendel wird nach links bis zur
Höhe h ausgelenkt und losgelassen. In der vertikalen Position
stößt der Faden
auf ein Hindernis.
Welche maximale
Höhe erreicht das
Pendel in der
rechten Position?
h
Lösung:
Am Anfang: K1 = 0 , U1 = mgh
Am Ende: K 2 = 0 , U 2 = mgh2 .
Zwangskräfte bleiben unberücksichtigt. Aus
dem Energieerhaltungssatz folgt h2 = h .
B3. Im Abstand h über dem
Ende einer ungespannten Feder befindet sich eine Masse
m. Sie wird ohne Anfangsgeschwindigkeit losgelassen.
Wie groß ist die maximale
Zusammendrückung der Feder?
Lösung: Sowohl Gravitations-
m
h
x
kraft als auch elastische Kraft sind konservativ.
Es gilt der Energieerhaltungssatz.
Am Anfang: K1 = 0 , U1 = mgh + 0
Am Ende: K 2 = 0 , U 2 = −mgx + c
x2
2
Energiesatz:
x2
. Daraus
2
mg ⎡
2hc ⎤
x=
⎢1 + 1 +
⎥ . Sonderfall: Bei h = 0
c ⎣
mg ⎦
ist x = 2mg / c - zwei Mal größer, als bei statischer Belastung.
mgh = − mgx + c
B4. Elastischer Stoß
(a) Zentrischer Stoß
Geschwindigkeiten vor dem
Stoß: v1 und v2 .
Geschwindigkeiten nach dem Stoß: v1′ und v2′ .
In einem abgeschlossenen System bleibt Impuls erhalten:
m1v1 + m2 v2 = m1v1′ + m2 v2′ .
(1)
Bei einem elastischen Stoß bleibt Energie erhalten:
2
2
2
2
m1v1 + m2 v2 = m1v1′ + m2 v2′ .
(2)
Diese Gleichungen können umgeschrieben
werden:
m1 ( v1 − v1′ ) = m2 ( v2′ − v2 )
(
)
(
m1 v1 − v1′ = m2 v2′ − v2
2
2
2
2
)
Wir teilen die zweite Gleichung durch die erste:
v1 + v1′ = v2′ + v2 oder v1 − v2 = − ( v1′ − v2′ )
(3)
Betrag der relativen Geschwindigkeit ändert
sich beim elastischen Stoß nicht.
Aus dem linearen Gleichungssystem (1) und
(3) folgt:
m v + m2 v2
m v + m2 v2
v1′ = − v1 + 2 1 1
v2′ = − v2 + 2 1 1
m1 + m2
m1 + m2
(b) Nicht zentrischer Stoß (hier nur Sonderfall
m1 = m2 , v2 = 0 ).
Der Impulserhaltungssatz nimmt die Form
G
G
G
G
m1v1 + m2 v2 = m1v1′ + m2 v2′
an. Energieerhaltung:
m1v12 + m2 v2 2 = m1v1′2 + m2 v2′ 2 .
Bei gleichen Massen bedeutet das
1
G G G
v1 = v1′ + v2′
v12 = v1′2 + v2′ 2 .
Aus der ersten Gleichung
ist ersichtlich, dass die
Vektoren
G G
G
v1 , v1′ und v2′ ein Dreieck
bilden. Die zweite Gleichung ist der Pythagoras-Satz. Daraus folgt,
dass dies ein rechtwinkliges Dreieck ist
( θ = 90° ): nach einem elastischen Stoß fliegen
die Kugeln unter einem rechten Winkel zu einander.
III. Gravitationsfeld einer Kugel
und
Eine dünne
Kugelschale
mit Masse m .
Masse des infinitesimalen Ringes:
ds
2π h ⋅ adθ
sin θ ⋅ dθ
dm = m
=m
= m⋅
.
2
2
4π a
4π a
2
Die durch den Ring erzeugte potentielle EnerGm ' dm
gie: dU = −
=
r
m'm
sin θ dϑ
= −G
2
2
R − 2 Ra cos θ + a 2
Die volle potentielle Energie:
π
Gm ' m
sin θ dθ
=
U =−
∫
2
2 0 R − 2 Ra cos θ + a 2
Gm ' m ⎡
( R − a)2 − ( R + a)2 ⎤
=
⎣
⎦
2 Ra
a
R > a:
U = −Gm ' m / R
II. Energieänderung beim plastischen Stoß
Betrachten wir noch einmal einen plastischen
Stoß, d.h. einen Zusammenstoß zweier Körper,
nach dem sie sich als ein Ganzes bewegen (an
einender kleben).
Die Wechselwirkungskräfte zwischen beiden
Körpern, unabhängig von deren Größe und
physikalischer Herkunft sind innere Kräfte.
Wirken am System keine weiteren Kräfte, so
ist das ein abgeschlossenes System. Der Impuls des Systems bleibt deshalb erhalten. Insbesondre gilt das für beliebige Zeitpunkte vor
und nach dem Stoß:
G
G
Impuls "vor": m1v1 + m2 v2
G
Impuls "nach" ( m1 + m2 ) v
b
1
2
2
2
2
⎛mv +m v ⎞
( m1 + m2 ) ⎜ 1 1 2 2 ⎟
2
2
⎝ m1 + m2 ⎠ − m1v1 − m2 v2
=
2
2
2
( m1v1 + m2v2 )
=
=
− m1v12 − m2 v22
2
( m1v1 + m2v2 )
(m v
=
2 2
1 1
=
2
m1 + m2
2
(
)
− m1v12 + m2 v22 ( m1 + m2 )
2 ( m1 + m2 )
) (
)
(
+ 2m1 v1 m2 v2 + m22 v22 − m12 v12 + m22 v22 − m1m2 v12 + v22
2 ( m1 + m2 )
(
2m1 v1 m2 v2 − m1m2 v12 + v22
2 ( m1 + m2 )
) = − m m (v
1
2
1
− v2
2 ( m1 + m2 )
)
2
und ist immer negativ: Energie geht bei einem
plastischen Stoß verloren.
U = −Gm ' m / a
IV. Kinetische Energie eines Mehrkörpersystems
Wenn keine äußeren Kräfte gewirkt haben:
G
G
G m1v1 + m2 v2
G
G
G
v
=
m1v1 + m2 v2 = ( m1 + m2 ) v ⇒
m1 + m2
Wie steht es mit der Energie der Körper?
Die Energieänderung ist gleich
( m + m2 ) v 2 − m1v12 − m2v22
∆K = K − K = 1
2
R<a:
)
0/
0→
m1
m2
02
0↑
0→
m5
m4
m3
→
m
G
v
Wir betrachten zwei Koordinatensysteme:
Laborsystem (x,y) und ein System, das sich
G
mit der Geschwindigkeit v des Schwerpunktes
bewegt (Schwerpunktsystem). Gegeben sind:
G
Geschwindigkeiten vi im Schwerpunktsystem
G
und Geschwindigkeit v des Schwerpunktes.
Zu bestimmen ist gesamte kinetische Energie.
Lösung: Geschwindigkeiten im Laborsystem
G
G G
sind vi ' = vi + v .
Die gesamte Kinetische Energie ist gleich
G G 2
mi ( vi + v )
mi vi '2
=∑
=
T =∑
2
2
GG
2
mi vi
mi 2vi v
m v2
=∑
+∑
+∑ i =
2
2
2
2
2
mv
G
G v
= ∑ i i + v ∑ mi vi + ∑ mi =
2
2
=0
m
2
2
mv
mv
=
+ ∑ i i
Kinetische
2
2
Energie im
„Kinetische Energie
des Schwerpunktes“
Schwerpunkt
System =
„innere Energie“
2