Berechnung einer Baugrube mit Abaqus

Berechnung einer Baugrube mit Abaqus∗†
A.Niemunis, Th.Meier, D.Rebstock
19. Oktober 2016
1
Inhaltsverzeichnis
1 Einführung
1
2 Aushub ohne Konsolidierung
2
2.1
Zur räumlichen Modellierung . . . . . . . . .
2
2.2
Definition eines FE-Netzes . . . . . . . . . . .
3
2.2.1
Knoten (Nodes)
. . . . . . . . . . . .
3
2.2.2
Elemente: . . . . . . . . . . . . . . . .
4
2.3
Balken . . . . . . . . . . . . . . . . . . . . . .
5
2.4
Flächen und Kontakte . . . . . . . . . . . . .
5
2.5
Anfangsbedingungen allgemein . . . . . . . .
7
2.6
Trockene Anfangsbedingung . . . . . . . . . .
8
2.7
Randbedingungen (RB) . . . . . . . . . . . .
9
2.8
Zeitlicher Ablauf und Diskretisierung . . . . . 11
2.9
Änderung des Modells während der Berechnung 11
2.10 Vorgespannte Anker und Steifen . . . . . . . 11
2.11 Beispiel (ohne Wasser, ohne Kontakte, ohne
Steife) . . . . . . . . . . . . . . . . . . . . . . 12
2.12 Kritisches Betrachten der Ergebnisse . . . . . 13
3 Aushub mit Konsolidierung
14
3.1
Konsolidierungselemente . . . . . . . . . . . . 14
3.2
Materialbeschreibung für die Konsolidierungsberechnung . . . . . . . . . . . . . . . . . . . 14
3.3
Undränierter Fall (grob) . . . . . . . . . . . . 14
3.4
Stoffgesetze
. . . . . . . . . . . . . . . . . . 14
3.5
AB für die Konsolidierungsberechnung . . . . 15
3.6
Mehr Flexibilität via USER
3.7
RB für Wasser . . . . . . . . . . . . . . . . . 16
3.8
Berechnung . . . . . . . . . . . . . . . . . . . 16
∗ Abaqus
. . . . . . . . . . 15
ist Markenzeichen der F-ma Simula.
† i11/didaktik/FE-Berechnung-inder-Geot-UEBUNG/FE-
Einführung
Die Hauptaufgabe bei einer FE-Berechnung der Baugrube
ist die Verformungsprognose im Umgebung des Aushubs.
Entscheidend für eine solche Prognose ist vor allem das konstitutive Verhalten des Bodens bei kleinen Verformungen.
Die Festigkeitsparameter sind zweitrangig, weil sie i.d.R.
nicht vollständig mobilisiert werden. Die Aufgabe bietet eine Gelegenheit besondere Flexibilität des FE-Programms
R
Abaqus
zu demonstrieren, u.a. die Änderung des Modells
während der Belastung (das Verschwinden der Elemente im
Aushub, Installation der vorgespannten Elemente), Umgang
mit Kontaktflächen, Definition der Anfangs- und Randbedingungen, Berechnung des Konsolidierungsvorgangs.
Bei der FE-Berechnung einer Baugrube sollen die folgenden
Aspekte berücksichtigt werden:
1. Bodenverhalten ist auch bei kleinen Verformungen stark
nichtlinar - Setzungen in der Umgebung der Baugrube
werden von dieser Nichtlinearität stark abhängig.
2. Bodenverhalten ist pfad- und zeitabhängig. Die zeitliche Abfolge des Aushubs kann berücksichtigt werden.
Sie hat Einfluss auf die Biegemomente der Wand in
verschiedenen Bauzuständen.
3. Untypische Situationen, z.B.: Geometrie der Baugrube, 3D-Effekte des Erddrucks, Einfluss der Vibration (Baumaschinen, Verkehr . . . ) erfordern sowohl eine raffinierte konstitutive Beschreibung als auch eine
komplizierte FE-Modellierung.
4. Die Bemessung nach EAB erfordert empirisch erhöhte
Erddruckansätze für einen verformungsarmen Verbau.
Die FE-Modellierung erlaubt dagegen eine direkte Verformungsprognose auch bei einer ungewöhnlichen Belastung oder Geometrie des Aushubs.
5. Der FE-Nachweis der Gebrauchstauglichkeit ist besonders interessant bei Anwesenheit von setzungsempfindlichen Altbebaungen.
6. Dimensionierung des Baugrubeverbaus mit einer FEBerechnung ist auch möglich. Sie wird aber i.d.R. nach
EAB berechnet. Diese Empfehlungen wurden algorithmisiert z.B. im Programm WALLS
http://www.fides-dvp.de/statik-hersteller/
fides/baugrubenberechnung/walls-baugrube/
Uebung.tex
R
Jede FE Berechnung mit Abaqus
benötigt vom Benutzer
eine Input-Datei, z.B. pit.inp. Sie wird mit einem Text
Editor (notepad++) nach den weiter beschriebenen Regeln
erzeugt und als eine Text-Datei gespeichert. Diese Datei
enthält Information über
1. Modell = Knoten + Elemente + Flächen + . . .
2. Kontakte
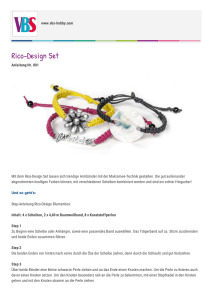
Abbildung 1: Ein großes Modell der Baugrube. Slomiński IBF Diss. Heft 169
a
b
3. Materialien = Eigenschaften der Elemente der Kontakte
a
h
4. Randbedingungen (RB)
a
5. Anfangsbedingungen (AB)
a = (2 bis 3) * max(h,b)
6. Step geostatic mit AB und mit dem Eigwengewicht
7. Steps mit Änderungen der Belastung der RB oder des
Modells
8. Anweisungen zum gewünschten Inhalt des Outputs
Die Berechnung startet man z.B. mit
abaqus j=1 inp=pit.inp
aus dem DOS-Fenster ”Eingabeaufforderung” im Verzeichnis wo pit.inp abgelagert wurde. Die Ergebnisse landen in
der Datei 1.odb und sich mit dem Programm Abaqus CAE
öffnen und angucken lassen.
Es ist empfohlen alle nichtlineare Teile der Aufgabe zunächst
auszuschalten, d.h.:
• Steps können ohne Option NLGEOM ausgeführt werden
(= nichtlineare Geometrie nach Hughes-Winget, siehe
Vorlesung 11 ”Numerik in der Geotechnik”)
• Materialeigenschaften können provisorisch als ELASTIC
definiert werden
• Kontakte können provisorisch fest verbunden werden
(z.B. mit PIN)
2
Aushub ohne Konsolidierung
Zunächst berechnen wir den Aushub als ein ebenes Problem, bei dem der Böden mit den CPE4 Elementen also
ohne Grundwasserströmung modelliert wird.
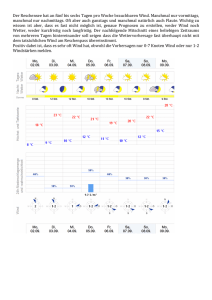
Abbildung 2: Empfehlung der DGGT
2.1
Zur räumlichen Modellierung
Bei der räumlichen FE-Modellierung einer Baugrube werden
die folgenden Aspekte berücksichtigt
1. Elementtypen Kontinuumselemente mit reduzierter/voller Integration, Konsolidierungselemente, Stäbe, Balken Federn, infinite Elemente für Dynamik (vor allem); Gefahr der shear locking bei der Modellierung
einer Schlitzwand mit Kontinuum-Elementen. Fehler
bei Durchbiegung kann sogar 500% betragen.
2. Ausnutzen von Symmetriebedingungen, spart Rechenaufwand. Ausnahme: Stabilitätsanalyse, z.B. eines Schachts
3. Wahl des Berechnungsausschnitts für die Diskretisierung. Orientierungswerte nach Empfehlungen Abschnitt
3 des Arbeitskreis 1.6 der DGGT ”Numerik in der
Geotechnik”:
Tiefe ≈ (2 bis 3)· Wandlänge,
Breite ebenfalls1 .
4. Ebene Verformung (Linienbauwerke) oder axialsymm.
(Pfähle, Säulen, CPT), 3D (Gurtung, Ecken, Gewölbewirkung)
5. Grosse Verformungen (NLGEOM bei STEPs)
1 Eine Kopie der DGGT-Empfehlungenliegt auf der homepage von
Niemunis unter ”Numerik in der Geotechnik”
6. Vereinfachte Unterteilung auf Schichten, evtl. spezielle Kompositelemente (parallele oder serielle Kopplung
ergibt eine transversale Isotropie)
7. Räumliche Diskretisierung :
- schwache Schichten genau,
- große Verformungsgradienten (Spannungskonzentrationen) genau
- Max B/5 unter dem Fundament
8. Je kleiner die Elemente, desto genauer ist das Ergebnis. Im Bereich der Wand genügen die Elemente mit
der Seitenlänge von etwa 20 cm (Orientierungswert)
9. Steifen (Federn, Stäbe, Balken, Kontinuumselemente)
Achtung auf Ausknicken ! (extra Knickanalyse: Handrechnung oder numerisch)
10. Achtung bei Verbindung von Elementen unterschiedlicher Knotenanzahl: Überlappung oder ”Lücken” dürfen
im Model nicht entstehen. Sie sollen mit MPCs oder
mit Übergangselemente verhindert werden.
11. Interfaces: Kontaktreibung zwischen der Wand und
dem Boden. Ein grosse Reibungswinkel (> 20◦ ) kann
manchmal zu numerischen Schwierigkeiten führen. Kontakte bei quadratischen Elemente, z.B. CPE8, schwieriger als bei linearen Elementen.
12. Kontaktflächen verwendet man für Schubverbund zwischen dem Gebirge und der Wand wenn eine relative
Bewegung zu erwarten ist. Die Rauhigkeit der Kontaktfläche ist vom Material und von der Herstellung
der Wand abhängig aber das Gleichgewicht der vertikalen Kräfte braucht dabei nicht berücksichtigt zu
werden (anders als in EAB).
13. Evtl. Berechnungsausschnitt aus dem Vergleich 3Dvs. 2D-Analyse bestimmen.
2.2
Definition eines FE-Netzes
Zuerst werden sämtliche Knoten (d.h. Eck- bzw. Zwischenpunkte) der zukünftigen Elemente definiert. Anschließend
werden die einzelnen Elemente unter Angabe des gewünschten
Typs generiert (z.B. 2D 4-Knoten Kontinuumselemente mit
ebener Verformung: CPE4[P], axialsymmetrisch 4-Knotenelement:
CAX4[P], das optionale P“ bewirkt, dass mit Porenwasserströmung gerechnet wird). Knoten und Elemente bzw. NSets
und ElSets werden wie folgt definiert.
2.2.1
Knoten (Nodes)
*NODE [,NSET= name ]
NodeNumber, x1 , x2 [, x3 ]
. . . zur Generierung von einzelnen Knoten.
Die Befehle
*NGEN [, NSET= name]
N1,N2, NNinc
oder
*NFILL [, NSET=name][, BIAS=b]
NSet1, NSet2, intervals, NNinc
...
501
502
401
401
402
402
301
301
201
102
2
103
205
104
3
Dabei muss darauf geachtet werden, dass alle Knoten NN1,
NN2, ... bereits existieren. Sie müssen für jedes Element
gegen den Uhrzeigersinn aufgelistet werden.
*ELGEN [, ELSET=Elset1 ]
Datenzeile
Die Datenzeile setzt sich wie folgt zusammen:
205
104
3
305
204
105
105
4
4
Elemente:
Die Standard-Syntax lautet:
*ELEMENT, TYPE=element type [,ELSET=Elset1 ]
EN, N N 1, N N 2, ...
305
204
103
2
1
304
203
2.2.2
405
405
304
203
102
1
303
202
101
404
404
303
202
101
403
302
505
504
403
302
201
2
503
5
5
a. Nummer des Muster-Elements (muss schon vorhanden
sein!)
Abbildung 4: Muster-Element und Muster-Zeile für *ELGEN b. Gesamtzahl der Elemente pro Zeile
c. Knoteninkrement innerhalb der Zeile von Element zu Element
d. Inkrement der Elementnummern innerhalb der Zeile
dienen zur Knotengenerierung zwischen zwei Knotennummern e. Anzahl der zu generierenden Zeilen
N 1 und N 2 oder Knotengruppennamen NSet1 und NSet2. f. Inkrement der entsprechenden Knotennummern von Zeile
Diese Gruppen müssen gleich viele Knoten enthalten und
zu Zeile
die Nummerierung muss zur angegebenen Anzahl von Ing.
Inkrement der entsprechenden Elementnummern von Zeitervallen und dem Knotennummer-Inkrement passen.
le zu Zeile
Die Knotengruppen seien definiert durch
Ein Beispiel dazu wurde in Abb. 4 dargestellt:
NSET, NSET= NSet1
ELGEN, ELSET=ALL
1, 2, 3, 4, 5 und
1, 10,
1,
1, 10, 100, 100
NSET, NSET=NSet2
mE, AnzahlE→, N-inc→, E-inc→, AnzahlZ↑, N-inc↑, E-inc↑
51, 52, 53, 54, 55
Eine Knotengruppe mit 30 Knoten wird durch:
Damit werden 10 Zeilen mit je 10 Elementen generiert. Alle
*NFILL, NSET=alle
Knoten müssen schon vorhanden sein. Die Knotennummer
NSet1, NSet2, 5, 10
erzeugt, d.h.
steigt um 1 wenn wir uns nach rechts bewegen und um 100
1, 2, 3, 4, 5
wenn wir uns nach oben bewegen. Identisch werden auch
11, 12, 13, 14, 15
die Elementnummer inkrementiert.
1
24, 25
34, 35
44, 45
54,55
face 3
4
face 1 2
1
Zum Beispiel, die Koordinaten des Knotens Nr 23 berechnen
sich aus der Interpolation x23 = x3 + 25 (x53 − x3 ).
3
face 2
21, 22, 23,
31, 32, 33,
41, 42, 43,
51,52,53,
face 4
3
elemok
3001 3002 3003 3004 3005 3006 3007 3008 3009 3010 3011 3012 3013 3014
Die BIAS-Option ermöglicht eine Konzentration der generierten Knoten zu einem der Ränder hin.
2901 2902 2903 2904 2905 2906 2907 2908 2909 2910 2911 2912 2913 2914
2901 2902 2903 2904 2905 2906 2907 2908 2909 2910 2911 2912 2913 2914
Der *NFILL-Befehl funktioniert nur mit NSets und nicht mit
Knotennummern!
2801 2802 2803 2804 2805 2806 2807 2808 2809 2810 2811
Mit
*NCOPY, OLD SET=NSet1, NEW SET=NSet2,
CHANGE NUMBER=∆NN, SHIFT
∆x1 , ∆x2 , ∆x3
wird der Knotensatz NSet1 um ∆x1 , ∆x2 , ∆x3 verschoben, der resultierende NSet2 hat die alten Knotennummern
plus ∆N N . Die Leerzeile (2. Datenzeile) ist obligatorisch.
Der *NSET-Befehl fasst die Knoten zu Sätzen zusammen (benennt eine existierende Knotengruppe):
*NSET, NSET=name
NN1, NN2, ..., NNn
*NSET, NSET=name, GENERATE
NN1, NNn, increment
Der Befehl *NSET erzeugt keine Knoten!
2701 2702 2703 2704 2705 2706 2707 2708 2709 2710
2701 2702 2703 2704 2705 2706 2707 2708 2709 2710 2711
2
3
aushub3
Littleexcavation
1
Abbildung 5: Das ELSET elemok wird von oben belastet
(Druck 5 kPa auf face-3) ELSET aushub3 wird entfernt mit
MODEL CHANGE, REMOVE
Für die Ansprache einer Gruppe der Elemente dient:
*ELSET, ELSET=ElSet [,GENERATE]
funktioniert analog zu *NSET.
Das Beispiel-Netz aus Abb. 4 wird nun vollständig generiert:
Es soll ein Quadrat von 1 m Kantenlänge mit 10x10 CPE4
Elementen generiert werden. Die obere linke Ecke soll im Ursprung liegen. Die Nummerierung der Knoten und Elemente
darf lückenhaft sein, muss aber in sich konsistent und eindeutig sein. Die Knoten des rechten und linken Rands werden zu NSets zusammengefasst (z.B. zum Aufbringen von
(Verschiebungs) RB, Einzellasten, Porenwasserdrücken), die
Randelemente entsprechend zu ElSets (z.B. zum späteren
Aufbringen von Flächenlasten oder zur Definition von Kon- mit den Eigenschaften
taktflächen bei Interaktionsproblemen.)
∗BEAM general s e c t i o n ,
...
∗∗
∗∗ K o n t e n d e f i n i t i o n
∗∗
∗NODE
1, 0, 0
11 , 1 , 0
∗NGEN, NSET=nunten
1 , 11 , 1
∗NCOPY, OLD SET=nunten , NEW SET=noben ,
CHANGE NUMBER=900 , SHIFT
0 , 10 , 0
∗NFILL , NSET=n a l l
noben , nunten , 9 , 100
∗NSET, NSET=n l i n k s , GENERATE
1 , 901 , 100
∗NSET, NSET=n r e c h t s , GENERATE
11 , 911 , 100
∗∗
∗∗ E l e m e n t d e f i n i t i o n
∗∗
∗ELEMENT, TYPE=CPE4
1,
1,
2 , 102 , 101
∗ELGEN, ELSET=a l l
1 , 10 , 1 , 1 , 9 , 100 , 100
∗ELSET , ELSET=l i n k s , GENERATE
1 , 901 , 100
∗ELSET , ELSET=r e c h t s , GENERATE
10 , 910 , 100
...
s e c t i o n=general , e l s e t=Balken
0 . 2 , 0 . 6 7 E−03 , , , , ,
0 , 0 ,−1
2 . 1 E+08 , 8 . 2 E+07
∗element , type=s p r i n g 2 , e l s e t=A u s s t e i f u n g
6001 , 9000 ,
3011
wobei in der 1. Datenzeile die Querschnittsfläche A = 0.2
3
10.23
=
m2 (pro lfm) und Trägheitsmoment I = bh
12 =
12
0.67 · 10−3 m4 (pro lfm) stehen. Für ebene Probleme ist
die 2. Datenzeile immer 0, 0, −1 (Orientierungsvektor). Die
3. Datenzeile beinhaltet die elastischen Steifigkeitsmodule
E = 2.1 108 kPa und G = 8.2 107 kPa.
2.4
Flächen und Kontakte
Die Flächen sind bei multipoint constraints (=MPC), bei
Definition der Kontaktfläche oder bei Definition der Belastung ganz nützlich. Eine einfache Form der Definition ist
die Angabe der Elemente, bzw. Elementsätze gefolgt durch
die Angabe der entsprechender Seite
∗Surface , type=ELEMENT, name=s u r f l o a d
10 , S3
11 , S3
...
Alternativ gibt es verschiedenste Netzgeneratoren die InputFiles für gängige FE Codes erzeugen können (z.B. ABAQUS Die Nummerierung der Seiten hängt von der Reihenfolge der
Knotennummerierung ab. Die Seite F1 (F=face) des EleCAE oder HyperMesh).
ments liegt zwischen den Knoten mit den lokalen Nummern
1 und 2; die Seite F2 zwischen den Knoten 2 und 3 usw.
,siehe Abb. 7
2.3 Balken
Eine biegsame Stützkonstruktion kann aus Balkenelementen
konstruiert werden, z.B.
∗ELEMENT, type=B21
5001 , 1411 , 1511
∗ELGEN, e l s e t=Balken
5001 , 16 , 100 , 1
21
F1
11
9000
6001
3011
5016
2911
5015
2811
5014
2711
5013
2611
5012
2511
5011
2411
5010
2311
5009
2211
5008
2111
5007
2011
5006
1911
5005
1811
5004
1711
5003
1611
5002
1511
5001
1411
Abbildung 6: Balken = Wand und Feder = Aussteifung
F4
100
F2
22
F3
12
*ELEMENT, TYPE=CPE4
100, 21, 11, 12, 22
Abbildung 7: Die Nummerierung der Seiten F 1 . . . F 4 wird
durch die Reihenfolge der Knotennummern in der Definition
des Elements impliziert.
Nach der Angabe der Name eines Elsets ohne Seitennummer, z.B.
∗Surface , type=ELEMENT, name=s u r t o p
topElements ,
leftElements ,
R
erkennt Abaqus
automatisch den ganzen freien Rand der
Elementgruppe
topElements und leftElements
Achtung: in Fällen wie in Abb. 8 werden bei den Eckelementen (markiert mit x in Abb. 8) zwei Seiten als surtop
gewählt
Bei einem 2D-Balken ist es erforderlich die Seite des Balkens
zu zeigen (mit SPOS oder SNEG) auf welcher die Fläche definiert wird. Werden die Knoten eines Balkenelements von
links nach rechts aufgelistet dann liegt SPOS oben und SNEG
unten, Abb. 9.
0 224
S5
SPO
SNEG
Aushub ?
A
B
B
A
Abbildung 9: Die Bezeichnungen (SPOS, SNEG) der Seiten
eines Balkenelements wird durch die Reihenfolge der Knotennummern in der Definition des Elements impliziert.
Master
104
*ELEMENT, type=B21
50,104,224
Master
Abbildung 8: Die Definition der Fläche ohne Seitennummer
beinhaltet die L-Häkchen an den Eckelementen.
31
1
Slave
surtop
B
A
1401 1411 5011 5031
PIN 1431
1401
11411
C
besser
leftElements
surtop
x
Aussteifung PseudoBalken
13011Balken
3001 3011 6611 6631
Slave
x
topElements
surtop
surtop
Spitze
Um eine Kontaktfläche (z.B. zwischen dem Balken und dem
Erdreich) zu definieren, benötigen wir zwei Reihen von Knoten. Für einen Balken mit Kontaktflächen auf beiden Seiten
erfordert dies drei Knotenreihen entlang des Balkens. Dafür
unterteilen wir das Erdreich in drei Teile A,B,C, Abb. 10
∗heading
d r e i F e l d e r und e i n Balken
∗∗ ∗∗∗∗∗∗∗∗ TEIL−C ∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗
∗node
1,
0.0 ,
0.0
31 , 1 5 . 0 ,
0.0
∗ngen , nset=Cunten
1 , 31 , 1
∗node
1401 , 0 . 0 ,
7.0
1431 , 1 5 . 0 ,
7.0
∗ngen , nset=Coben
1401 , 1431 , 1
∗nset , nset=CobenGLUE , generate
1411 , 1431 , 1
∗NFILL , nset=Cknoten
Cunten , Coben , 14 , 100
∗nset , nset=C l i n k s , generate
1 , 1401 , 100
∗nset , nset=C r e c h t s , generate
31 , 1431 , 100
∗element , type=c p e 4
1 , 1 , 2 , 102 , 101
∗elgen , e l s e t=a l l e C e l e m e n t e
1 , 30 , 1 , 1 , 14 , 100 , 100
∗∗ ∗∗∗∗∗∗∗∗ TEIL−A ∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗
∗nset , nset=Aunten , generate
1401 , 1411 , 1
∗node
3001 , 0 , 15
3011 , 5 , 15
∗ngen , nset=Aoben
3001 , 3011 , 1
∗NFILL , nset=Aknoten
Aunten , Aoben , 16 , 100
∗nset , nset=A l i n k s , generate
1401 , 3001 , 100
∗nset , nset=A r e c h t s , generate
1411 , 3011 , 100
∗element , type=c p e 4
1401 , 1401 , 1402 , 1502 , 1501
∗elgen , e l s e t=a l l e A e l e m e n t e
1401 , 10 , 1 , 1 , 16 , 100 , 100
∗∗ ∗∗∗∗∗∗∗∗ TEIL−B ∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗
Abbildung 10: Diskretisierung für Kontakflächen.
∗node
5011 , 5 . 0 , 7 . 0
5031 , 1 5 . 0 , 7 . 0
∗ngen , nset=Bunten
5011 , 5031 , 1
∗node
6611 , 5 . 0 , 1 5 . 0
6631 , 1 5 . 0 , 1 5 . 0
∗ngen , nset=Boben
6611 , 6631 , 1
∗NFILL , nset=Bknoten
Bunten , Boben , 16 , 100
∗nset , nset=B l i n k s , generate
5011 , 6611 , 100
∗nset , nset=B r e c h t s , generate
5031 , 6631 , 100
∗element , type=c p e 4
1411 , 5011 , 5012 , 5112 , 5111
∗elgen , e l s e t=a l l e B e l e m e n t e
1411 , 20 , 1 , 1 , 16 , 100 , 100
∗∗ ∗∗∗∗∗∗∗ BALKEN ZWISCHEN A UND B ∗∗∗∗∗∗
∗ncopy , o l d s e t=A r e c h t s , new s e t=b a l k e n k n o t e n ,
changenumber=10000 , s h i f t
0.0 , 0.0
∗element , type=B21
5001 , 11411 , 11511
∗elgen , e l s e t=Balken
5001 , 16 , 100 , 1
∗ e l s e t , e l s e t=B a l k e n O h n e S p i t z e , generate
5002 , 5016 , 1
∗element , type=B21
8001 , 1411 , 1511
∗elgen , e l s e t=PseudoBalken
8001 ,
16 ,
100 ,
1
(∗mE , AnzahlE , Ninc , E i n c ∗ )
∗∗ ∗∗∗∗∗∗∗∗∗∗∗∗∗∗ KLEBEN B UND C UND SPITZE ∗∗∗∗∗∗∗∗
∗MPC
PIN ,
Bunten , CobenGLUE
∗MPC
PIN , 11411 ,
1411
∗∗
Beachte die obligatorische leere Zeile am Ende von *ncopy. Die Rauhigkeit wird definiert mit
Damit sind die Seiten des Balkens vom Erdreich A und B ∗∗ Def . R a u h i g k e i t : 1 . 0 = D i c k e i n x 3 , 0 . 3 6 4
getrennt (bis auf den Knoten an der Spitze). Noch muss die ∗surface i n t e r a c t i o n , name=z w e i d r i t t e l p h i
Feder auf einen neuen Knoten verlegt werden
1.0
∗node
9000 , 0 . 0 , 15
∗element , type=s p r i n g 2 , e l s e t=A u s s t e i f u n g
6001 , 9000 , 13011
= t a n 20 ◦
∗Friction
0.364
∗surface behavior , no s e p a r a t i o n
Die Situation vor der Wand ist komplizierter, weil dort die
Elemente des Aushubs zu einem späteren Zeitpunkt entfernt werden müssen. Die Oberfläche würde danach ohne die
∗node
unterliegenden Elemente bleiben. Die Kontaktfläche trägt
9000 , 0 . 0 , 15
dann zwar keine Kontaktkräfte aber die fehlenden Elemen∗element , type=T2D2 , e l s e t=A u s s t e i f u n g
te führen zu numerischen Problemen (die durch keine Ele6001 , 9000 , 13011
mente verbundenen Knoten führen zur singulären SteifigKontakt zwischen dem Balken und dem Erdreich besteht keitsmatrix). Um dies zu verhindern definieren wir künstlich
aus der MASTER Fläche (ein Polygon, das nicht durchdring- einen Pseudo-Balken mit einer vernachlässigbaren Steifigbar für die kontaktierten Knoten ist) und aus der SLAVE keit. Er verbindet die Knoten auf der rechten Seite des Bereichs A und dient für die Definition der Oberfläche. Nach
Fläche (eigentlich eine Liste von Knoten aber nicht mit dem Aushub bleibt der Pseudo-Balken stehen und unterstützt
NSET sondern mit SURFACE definiert). Bei unterschiedlicher die Kontaktfläche (auch wenn ohne Kräfte). Diese Prozedur
Diskretisierung des Randes soll grober diskretisierte Rand erfolgt mit
als MASTER gewählt werden. Die Flächen des Balkens wer∗ e l s e t , e l s e t=VorBalkenElement , generate
den mit SLAVE definiert. Als MASTER wählt man i.d.R. die 1410
, 2910 , 100
Flächen des Bodens, weil sie ”überzogen” (mit L-Häkchen) ∗surface , name=V o r B a l k e n S u r f a c e
definiert werden können. Solche ”überzogene” MASTER Flächen PseudoBalken , SNEG
verhindern, dass SLAVE Knoten infolge einer relativen Ver- ∗surface , name=V o r B a l k e n B a l k e n S u r f a c e
B a l k e n O h n e S p i t z e , SPOS
schiebung hinter die MASTER Fläche geraten und dort blockiert ∗CONTACT
PAIR ,
werden. Um solche Gefahr zu meiden, müsste man die gan- INTERACTION
=z w e i d r i t t e l p h i
ze Oberfläche der linke Spalte der Elemente aus B (mit L- V o r B a l k e n B a l k e n S u r f a c e , V o r B a l k e n S u r f a c e
Häkchen) als SURFACE definieren
Die Reihenfolge der INTERACTION-Liste ist von Bedeutung.
∗ e l s e t , e l s e t=H i n t e r B a l k e n E l e m e n t , generate
Die erste Fläche wird als Slave und die zweite als Master
1411 , 2911 , 100
∗surface , name=H i n t e r B a l k e n S u r f a c e
interpretiert.
oder ein Stab (T = truss) statt Feder
∗∗ H i n t e r B a l k e n E l e m e n t , S4
HinterBalkenElement ,
und nicht nur die S4 Seite von HinterBalkenElement. Wir
entscheiden uns aber trotzdem für die S4 Variante:
2.5
Anfangsbedingungen allgemein
Die Anfangsbedingungen definiert man nach der Beschreibung der Geometrie (Knoten, Elemente) und der Materia• Die Spitze (Knoten 11411) des Balkens wird ohnehin leigenschaften. In geotechnischen Berechnungen werden die
mit dem Boden verbunden (*MPC mit PIN)
geologischen Prozesse der Sedimentation nicht nachgerechnet sondern der aktuell vorhandene Zustand in-situ wird
• Die Slave Knoten sind mit dem elastischen Balken ver- als ”undeformiert” (x, t=0) = 0 angenommen. Die Setbunden also können nicht ”plastisch” über die Master
zungen (und die horizontalen Verschiebungen) werden von
Fläche fließen.
dem Zustand vor dem Aushub gemessen. Manchmal ist es
sinnvoller, die Setzungen von einem anderen Bauzustand zu
• Die Master Polygon wird abgerundet (default
berechnen , z.B. vom Zeitpunkt wenn die Konstruktion sta*contact pair, smooth=0.2),
tisch unbestimmt geworden ist. Anders als bei Stahlbau ist
womit der Kontakt des oberen Knotens (13011) des die undeformierte Konfiguration im Boden nicht spannungsBalkens verloren geht.
frei. Deshalb muss der Anfangsspannungszustand (ein Feld
σ(x, t=0) 6= 0 definiert werden. Ähnlich soll der SpannungsDie Definition der Kontaktfläche hinter der Wand (auf der zustand in den vorgespannten Ankern definiert werden.
rechten Seite) besteht aus folgenden Teilen:
Alle moderne Stoffgesetze der Bodenmechanik benutzen als
Zustandsvariable nicht nur die Spannung sondern auch die
• Wahl der Elementengruppe des Bereichs B und ihre Porenzahl (oder eine äquivalente Variable, z.B. p im Came
Oberfläche = Master
clay Modell). Deshalb soll i.d.R. auch das Anfangsfeld der
• Wahl der rechten Oberfläche (SNEG) der Wand = Slave Porenzahl e(x, t=0) definiert werden.
• Definition des Kontakts zwischen Master und Slave
Diese Prozedur erfolgt mit
∗ e l s e t , e l s e t=H i n t e r B a l k e n E l e m e n t , generate
1411 , 2911 , 100
∗surface , name=H i n t e r B a l k e n S u r f a c e
H i n t e r B a l k e n E l e m e n t , S4
∗surface , name=H i n t e r B a l k e n B a l k e n S u r f a c e
B a l k e n O h n e S p i t z e , SNEG
∗CONTACT PAIR ,
INTERACTION=z w e i d r i t t e l p h i
HinterBalkenBalkenSurface , HinterBalkenSurface
∗∗ ∗ 1 . s l a v e
∗∗∗∗∗∗∗
2 . m a s t e r ∗∗∗∗∗∗∗
1. Anfangsspannungen als K0 -Zustand:
• Nur für normalkonsolidierte Böden gilt K0 ≈
1−sin ϕ. Für überkonsolidierte Böden kann sogar
K0 > 1 (London clay) erforderlich sein.
• Bei horizontaler GoK ist die vertikale und die horizontale Spannungskomponente die Hauptspannungen zu definieren. Eine z.B. vertikal zunehmende Schubspannung τ ist aber nicht erlaubt,
siehe Skript BM II, Kapitel ”Grenzzustände nach
Rankine”
• Transversale Isotropie bzw. Orthotropie (in geologischen Maßstäben) kann via K0 x1 6= K0 x3
eingegeben werden
• Bei einer Baugrube in der Böschung soll das Feld
der Anfangsspannung wie in der BM II im Kapitel ”Grenzzustände nach Rankine” vorgegeben
werden. Eine solche Definition ist mit Hilfe von
*INITIAL CONDITIONS,TYPE=STRESS,GEOSTATIC
leider nicht möglich.
2. Bei einer hügeligen GoK kann eine elastische Berechnung mit einer Poissonzahl ν aus K0 ≈ ν/(1 − ν)
verwendet werden, um das Anfangsfeld σ(x, t=0) zu
erzeugen. Dafür:
• setzt man die Anfangsspannung zu Null
• bringt man das Bodeneigengewicht in einem STEP
ohne NLGEOM auf
• führt man die elastische Berechnung des Anfangsgleichgewichts aus
• schreibt man die erhaltene Spannung in einer externen Datei auf
∗INITIAL CONDITIONS, TYPE=STRESS , GEOSTATIC
(1)
(1)
(2)
(2)
elset, σ22 , x2 , σ22 , x2 , K0x1 , K0x3
wobei die ’senkrechte’ Richtung x2 für 2D durch x3 für 3D
ersetzt wird. Das Eigengewicht aus Gravitation GRAV wird
im ersten *STEP aktiviert für die Materialien mit definierten DICHTEn. Der STEP mit dem geostatischen Gleichgewicht
hat die Form
∗STEP
∗GEOSTATIC
∗DLOAD
elset, GRAV,g, ~g1 , ~g2 , ~g3
...
∗END STEP
Die Gravitation g wird durch den Betrag g = kgk und durch
die Neigung des normalisierten Vektors ~g mit Komponenten in 1-, 2- und 3-Richtung definiert, z.B. {~g1 , ~g2 , ~g3 } =
{0, −1, 0} für 2D und {~g1 , ~g2 , ~g3 } = {0, 0, −1} für 3D
Anschließend startet man die Berechnung mit einem Ein Beispiel für das Anfangsgleichgewicht:
geeigneten bodenmechanischen Stoffgesetz und verwendet das aus der elastischen Berechnung erhaltene
x2
Spannungsfeld als die Anfangsspannung für die einp = 5kPa
gentliche Berechnung. Eine ähnliche Prozedur kann
man auch bei schräg liegenden Bodenschichten verx 2 =15
elemok
T22 = 5kPa
wenden. Es ist empfohlen das maximale Spannungs1
1
1
1
verhältnis aus der elastischen Berechnung in allen Ele1+sin ϕ
3
menten zu überprüfen (z.B., ob σmax /σmin < 1−sin
ϕ
γ = 20 kN/m
gilt).
3. Ein nach unten abnehmendes Feld der Porenzahl wird
i.d.R. vorgegeben.
x2 = 0
T22= 305kPa
4. Die räumliche Fluktuationen der Spannung und Porenzahl kann bei Prognose der Differenzialsetzung bei Abbildung 11: Anfangsspannung (Gesamtspannung bei
statisch unbestimmten Konstruktionen von besonde- CPE4 oder effektive Spannung bei CPE4P)
rer Wichtigkeit sein. Räumliche Korrelation der stochastischen Verteilung der Parameter macht das Zufallsfeld unabhängig von der Diskretisierung
∗SOLID SECTION, ELSET=a l l e , MATERIAL=sand
∗MATERIAL, NAME=sand
5. Eine möglich genaue Initialisierung des Porenzahl-Feldes ∗ELASTIC
1 0 . E3 , 0 . 2 5
ist meistens sehr wichtig:
(a) Unterschied Kontraktanz/Dilatanz (dadurch sehr
grosse Unterschiede bei undränierter Festigkeit =
bei schneller Belastung )
(b) unterschiedlicher Kriechraten (gefährlich bei statisch unbestimmten Bauwerken)
(c) Unterschiedliches Verhalten bei Akkumulation infolge einer zyklischen Belastung
6. Korrekte (zeitlliche) Abfolge ist ein Muss bei Plastizität. Eine präzise Reihenfolge in welcher die Lasten
und Modell-Änderungen berücksichtigt werden ist unabdingbar.
2.6
Trockene Anfangsbedingung
Die Anfangsspannung definieren wir mit
∗INITIAL CONDITIONS, TYPE=STRESS
elset, σ11 , σ22 , σ33 , σ12 , σ13 , σ23
oder mit
∗DENSITY
2.0
...
∗INITIAL CONDITIONS, TYPE=STRESS , GEOSTATIC
a l l e , −5.0 , 15 , −305.0 , 0 . 0 , 0 . 5
∗STEP
∗GEOSTATIC
∗DLOAD
a l l e , GRAV, 10 , 0 , −1 , 0
elemok , P3 , 5
∗END STEP
Erläuterung des Beispiels:
das Eigengewicht γ = 20 kN/m3 ergibt sich aus der Dichte2
*DENSITY 2.0 t/m3 und aus der Gravitation GRAV 10 m/s2
in der Richtung −x2 .
Die Flächenlast auf der GoK bei x2 = 15m beträgt 5 kPa
(wirkt auf die P3-Seite der Elemente elemok an der OK).
Die vertikale Spannung (Kompression negativ) in der Elementgruppe alle ist damit σ22 = (x2 − 15) · 20 − 5 kPa.
Nach der Angabe
2 Bei einer Berechnung mit CPE4 wird als *DENSITY die feuchte Dichte ρ angegeben. Bei CPE4P wird als *DENSITY trockene Dichte ρd erfordert, siehe die Berechnung mit Konsolidierung.
∗INITIAL CONDITIONS, TYPE=STRESS , GEOSTATIC
a l l e , −5.0 , 15 , −305.0 , 0 . 0 , 0 . 5
R
iterpoliert Abaqus
σ22 zwischen den Werten -305 kPa und
-5 kPa für die Koordinaten x2 = 0 bzw. 15 m. Eine andere
Interpolation als entlang x2 in 2D oder entlang x3 in 3D ist
nicht möglich. Die Schubkomponenten der Spannung (z.B.
in einer unendlichen Böschung) können nicht definiert werden. Der Erddruckbeiwert wurde im Beispiel als K0 = 0.5
vorgegeben (die letzte Zahl in der Datenzeile). Die verteilte
Last *DLOAD beinhaltet u.a. eine GRAV -Zeile. Sie beschriebt
die Gravitation, in diesem Beispiel g = {0, −10, 0}.
DOF4..6 = Verdrehungen
DOF8 = Porenwasserdruck
Die folgende RB für nset in einem *STEP setzt die u2 Komponente der Verschiebung auf einen neuen Wert u0 (und
nicht ”ändert um” u0 ):
*BOUNDARY, OP=MOD
nset, 2, 2, u0
Ähnliches kann in jedem STEP erscheinen. Diese RB bewirkt
eine Verschiebung der Knoten in nset um u0 in 2-Richtung
und ist sehr nützlich, z.B. für Stützensenkung, vorschubDas Anfangsgleichgewicht soll ohne Knotenverschiebung(!) gesteuerter Triaxial- oder Ödometerversuch, Grundwassererfüllt werden, unabhängig vom Material. Im globalen Gleich- spiegeländerungen). Der Wert u0 ist als Verschiebung von
gewichtssystem K · u = R soll der Belastungsvektor ver- der Anfangskonfiguration zu verstehen.
schwinden 3 , d.h.
Standard Option ist OP=MOD(ify), hier werden nur Änderungen
Z
Z
Z
angegeben. u0 ist aber kein Inkrement der Verschiebung im
0
Rαi =
Nα ti dS +
Nα fi dV −
Bkl αi σkl
dV = 0αi , aktuellen Schritt. Die Option OP=MOD bewirkt lediglich, dass
St
V
V
die RB aus früheren STEPs an anderen Freiheitsgraden unverändert weiter gelten. Im betreffenden STEP ändern die
wobei das Paar der Indizes α (=Knotennummer) und i (=Rich-gewählten Freiheitsgrade ihre Werte linear (default) von
tung) einem globalen Freiheitsgrad entspricht
Summe dem aktuellem (am Anfang des STEPs) zu dem vorgegebeP Die
über alle Elemente verbirgt sich unter V =
V e.
nem u0 (am Ende des STEPs).
Durch eine Kontrolle der Verschiebungen nach dem ersten Bei Verwendung von OP=NEW werden alle zuvor definierten
*STEP kann man sehr einfach zu prüfen, ob das Spannungs- RB gelöscht und müssen ggf. neu definiert werden.
feld richtig initialisiert wurde.
Kopplung von Freiheitsgraden einzelner Knoten:
Das multipoint constraint *MPC ist eine Zwangsbedingung,
die verschiedene Freiheitsgrade miteinander koppelt, z.B.
uαi = uβj . Dies geschieht unabhängig von der Steifigkeit
der
Elemente. *MPCs können mit verschiedenen Optionen
Die Randbedingungen können an allen Knoten (also nicht
nur am ”Rand” im geometrischen Sinne) definiert werden. (PIN, TIE,*EQUATION) angegeben werden. Intern wird ein
Die natürlichen (Neumann) RB werden als Belastungen (via *MPC durch Koeffizienten von a in der linearen Gleichung
*CLOAD, *DLOAD, *DSLOAD) vorgegeben. Nur die essentielaT · u − a0 = 0
(1)
len (Dirichlet) RB werden unter dem Schlüsselwort *BOUNDARY
eingeführt. Nicht nur Verschiebungen sondern auch PWDoder Temperatur-Knotenwerte können mit *BOUNDARY de- definiert, in unserem Beispiel aαi = 1, aβj = −1 und Rest
finiert werden. Die RB (nur die Variante ohne Optionen) Null. Man kann eine zusätzliche Nebenbedingung nicht einkönnen bei der Beschreibung des Modells oder in einzelnen fach dem globalen Gleichungssystem anhängen und das SyBelastungsschritten definiert werden. Die RB-en können von stem dadurch überbestimmt machen. Um (1) zu erfüllen
Step zu Step geändert, OP=MOD, oder neu definiert, OP=NEW, benötigt man (z.Z. unbekannte) verallgemeinerte Reaktion
die den Belastungen überlagert werden sollen (wie bei einem
werden.
Auflager uβj = 0).
Fixierung einzelner Freiheitsgrade:
2.7
Randbedingungen (RB)
Angabe der Knotenwerte (VerschiebungsRB, Porenwasserdrücke (ggf. veränderlich), Temperatur) erfolgt mit
*BOUNDARY, OP=[MOD/NEW]
nset, DOF1, DOF2
Die Freiheitsgrade DOF1 bis DOF2 der Knotengruppe nset
werden zu Null gesetzt (falls am Anfang des des STEP’s noch
nicht gleich Null dann linear auf Null innerhalb des STEP’s
gefahren). Mit *BOUNDARY, OP=[MOD/NEW]
nset, DOF1, DOF2, value
werden die Freiheitsgrade DOF1 bis DOF2 werden zu value
innerhalb des STEP’s gefahren. Der Wert value wird von undeformierten Konfiguration gemessen, d.h. us handelt sich
hier um kein Inkrement, auch nicht dann, wenn die Option
*BOUNDARY, OP= MOD angegeben wird.
Mit der Variante
*BOUNDARY, FIXED
nset, DOF1, DOF2
werden DOF1 BIS DOF2 bei aktuellen Werten fixiert (keine
Änderungen möglich im betreffenden STEP möglich).
Die Freiheitsgrade (= DOFs = degrees of freedom) sind bei
allen Kontinuumselementen identisch nummeriert:
DOF1..3 = Verschiebungen
3 vgl.
”Numerik in der Geotechnik”, Vorlesung 7
Drei Methoden verwendet man für *MPC in der Literatur.
Die ”Penalty” Methode addiert den mit λ kKk vergrößerten Fehler λ(aT · u − a0 )2 zur potentiellen Energie
und bildet damit man die erweiterte pot. Energie Π = u ·
K · u − R · u + λ(aT · u − a0 )2 . Das Minimum von Π bei Variationen δu berücksichtigt das MPC. In der Lagrange’sche
Methode wird die potentielle Energie dagegen zu Π̄ = u ·
K · u − R · u + λ̄(aT · u − a0 ) erweitert (mit unbekanntem
λ̄). Die Lösung findet man aus δΠ = 0 infolge der Variationen δu und δ λ̄. (Lagrange’sche Multiplikator λ̄ wird als
R
Reaktion zum MPC berechnet). Abaqus
benutzt die Kondensationsmethode. Gl. (1) wird mit a0 = 0 verwendet und
umgestellt
X
uαi = āT · ū oder uαi =
āβj ūβj
(2)
βj6=αi
wobei ū kürzer als u ist (um die αi -te Komponente). Analog
ā ist kürzer als a und kann aus dem Vergleich von (1) und (2)
berechnet werden. In K · u = R kann die Zeile zαi · u = Rαi
gestrichen weren. Sie gilt nicht, weil die Reaktion zur MPC
bei Rαi fehlt. Die restlichen Zeilen werden mit (2) wie folgt
kombiniert. Die Spalte k̄αi der gedrungenen Matrix K wird,
∗EQUATION
statt mit uαi , mit der rechten Seite von (2) multipliziert.
Aus K bildet man eine reduzierte Steifigkeit K̄ ohne αi -te
Zeile und αi -te Spalte und aus u und R bilden wir ū und
R̄ durch Entfernung jeweils der αi -ten Komponente. Die
K*u = R
- - K*u = R
k αi
N
nset1, DOF1, A1 , ... ,nsetN, DOFN , AN
wobei N die Anzahl der Summands auf der linken Seite von
(4) bezeichnet. Die Zweite Zeile beschreibt die Freiheitsgrade und die Faktoren in einzelnen Summands.
Beispiel: Knoten 100 soll sich immer genau so weit in 1Richtung bewegen wie Knoten 200:
∗EQUATION
2
100, 1, 1, 200, 1, -1
αi
* =
* =
oder nset1 soll sich halb so weit in 1- wie nset2 in 2-Richtung
bewegen:
x
αi
∗EQUATION
2
Abbildung 12: Modifikation des Gleichungssystems mit nset1, 1, 1, nset2, 2, -2
MPC: der Freiheitsgrad αi wird eliminiert.
Der Freiheitsgrad des zuerst genannten Knotens (nset1) wird
aus dem Gleichungssystem eliminiert, kann also hinterher
kondensierte Form
nicht mehr mit z.B. *BOUNDARY oder *CLOAD angesprochen
werden.
K̄ · ū + k̄αi uαi = K̄ + k̄αi āT · ū = R̄
(3)
(Ober-)Flächenlasten:
mit der Dyade k̄αi āT kann direkt gelöst werden4 .
Auch eine wie in Abb. 13 dargestellte RB kann mit MPC
beschrieben werden.
Die Lasten werden statisch (ggf. alternierend) oder dynamisch: lotrecht, horizontal (Bremskräfte) definiert.
Flächenlasten werden mit dem *DLOAD-Befehl (distributed
loads) definiert und das nur innerhalb von (Berechnungs-)
*STEPs, sie gehören nicht zur eigentlichen Modelldefinition.
Allgemeine Syntax:
∗DLOAD
elset, loadtype, load
α
Abbildung 13: Das bewegliche Auflager auf einer Böschung
kann mit *EQUATION definiert werden.
Die Lastart (loadtype) hängt von der jeweiligen Anwendung und den verwendeten Elementen ab. Für z.B. Gleichstreckenlasten bei viereckigen Kontinuumselementen gibt es
P1, P2, P3 und P4. Das P“ steht für pressure und die Zahl
gibt die gewünschte Seite”(Kante, oder face in Abaqus Manual) an. Die Nummerierung ist abhängig von der Knotenreihenfolge bei der Elementdefinition.
Sollen sich Freiheitsgrade (Verschiebungen, Verdrehungen, Parameter OP=MOD (Default) wie zuvor bedeutet:
Porenwasserdrücke) einzelner Knoten abhängig von Freiheitsgraden anderer Knoten ändern, gibt es zwei verschie1. der gesamte Wert der Belastung muss definiert werden
dene Möglichkeiten, dies im input-file zu realisieren (*MPC
(es ist also kein Inkrement bezüglich des vorherigen
und *Equation):
Steps)
∗MPC
2. die vorherigen Belastungen an anderen Stellen werden
beibehalten
PIN, nset1, nset2
oder
3. die Belastung wird innerhalb des STEPs vom aktuellen
Wert auf den vorgegebenen Wert am Ende des STEPs
linear (default) geändert.
∗MPC
TIE, nset1, nset2
erzwingt gleiche Verschiebungen (PIN, DOF1,2 u. 3) bzw.
Gleichheit sämtlicher Freiheitsgrade der Knoten (TIE) in Parameter OP=NEW bedeutet, dass die vorherigen Belastunden beiden nsets.
gen an anderen Stellen auf Null reduziert werden. Die DateiFlexibler ist der *EQUATION-Befehl mit dessen Hilfe folgende Zeile besteht aus dem Namen der Fläche, Typ der Belastung, z.B. P für pressure, und Wert
Gleichung definiert wird:
Nützliche Variante von *DLOAD bietet *DSLOAD.
Q
R
A1 uP
i + A2 uj + ... + AN uk = 0
(4)
dabei ist uP
i eine Knotenvariable des Knoten P, Freiheitsgrad i und An sind beliebige feste Koeffizienten. Die allgemeine Syntax lautet:
4 Für
a 6= 0 lässt sich die Methode
einfach
erweitern. Wir haben (3)
in der Form K̄ · ū + k̄αi uαi = K̄ + k̄αi āT · ū = R̄ − k̄αi a0
∗DSLOAD, OP=MOD
topsurf , P, 100.0
Der Vorteil bei *DSLOAD ist, dass man nicht auf die Seiten
der einzelnen Elemente achten muss sondern eine Flächendefinition
nutzt.
Der Druck auf die Oberfläche (via Befehle *DLOAD oder
*DSLOAD) wird bei geometrisch nichtlinearen Berechnungen
(d.h. mit *STEP, NLGEOM) als Folgelast betrachtet. Er steht
?
OK
NLGEOM
Abbildung 14: Folgelasten richtig und falsch angesetzt.
links , 1 , 1
rechts , 1 , 1
unten , 2 , 2
9000 , 1 , 2
∗CONTROLS, ANALYSIS=DISCONTINUOUS
∗NODE OUTPUT
U
∗ELEMENT OUTPUT, p o s i t i o n=n o d e s
S, E
∗end step
Im einem Schritt werden mit *boundary, fixed alle Knosenkrecht zur Oberfläche des Elements auch nach der Ver- ten festgehalten und einige Elemente mit
formung. Es ist für eine verteilte Last aus dem Wasserdruck
richtig, aber falsch bei einer Aufschüttung, Abb. 14. Die ∗model change , type=element , remove
Komponenten der Knotenlasten (*CLOAD) werden in globalen kartesischen Komponenten angegeben und ändern sich werden entfernt. Im nächstem Schritt werden die Knoten
nicht bei Deformation.
allmählich losgelassen (bis auf die neu definierten RB-en).
Bei bodenmechanischen Stoffgesetzen soll Druck Null vermieden werden. Dafür wird eine kleine ”künstliche” Ober2.10 Vorgespannte Anker und Steifen
flächenlast oder eine kleine Kapillarkohäsion vorgegeben.
2.8
Zeitlicher Ablauf und Diskretisierung
1. Krafteinleitung in den Boden soll nie über nur einen
Knoten modelliert werden sondern über einen Verpresskörper.
1. Ablauf so genau wie möglich, da Stoffverhalten pfadabhängig, d.h. Eigengewicht des Untergrunds, ggf.
Nachbarbebauung, ggf. Absenken des Grundwassers,
Berücksichtigung des Bauablaufs:
Aushubstufen = Anker / Steifen-Abstand sonst maximal h/3,
Anker/Steifeneinbau + ggf. Vorspannung
2. Inkrementierung: Jeder step wird in Zeitinkremente
unterteilt, die ausreichend klein sein müssen aufgrund
Nichtlinearität des Stoffgesetz; Orientierungswert 500 Abbildung 15: Einleitung der Ankerkraft in Boden über
bis 1000 Inkremente pro step bei Verwendung von mehrere Knoten
(Visko-) Hypoplastizität . Ausnahme: Anfangsgleichgewicht soll in einem Zeitinkrement erfolgen, nur dann
2. Die Vorspannung kann man über ein Kräftepaar einGleichgewicht der inneren und äußeren Kräfte und keigeleitet werden am Kopf und in der Mitte des Verne Deformationen.
preßkörpers
3. Bei Verwendung von zeitabhängigen Stoffgesetzen, muss
3. Anker haben in Wirklichkeit ein 3D Tragverhalten,
reale Zeit verwendet werden.
das i.Allg. nicht ohne Weiteres 2D modelliert werden
kann (räumliche Verspannung). Das Tragverhalten in
∗STEP ,INC=1000 ,NLGEOM
2D Berechnungen hängt von der Diskretisierung im
∗STATIC
Bereich der Krafteinleitungsstrecke ab.
∆tini , tEnde , ∆tmin , ∆tmax
2.9
Änderung des Modells während der Berechnung
Angenommen alle *Nsets und *Elsets wurden bereits sinnvoll definiert kann man den Aushub mit folgenden Schritten
simulieren:
∗step , nlgeom
S c h r i t t −2 = 1 . Aushub : Elemente l o e s c h e n
∗static , d i r e c t
1 ,1
∗boundary , f i x e d
alleknoten ,1 ,6
9000 , 1 , 2
∗model change , type=element , remove
aushub1
∗end step
.............
.............
∗step , extrapolation=no , nlgeom , INC=100000
S c h r i t t −4 Knoten an n e u e r O b e r f l a e c h e l o e s e n
∗static
0.001 , 1.0 , 0.0001 , 0.1
∗boundary , op=new
4. Bei Herstellung kann es zu Auflockerung im Bereich
der freien Ankerlänge (vor dem Verpresskörper) kommen! Durch Anpassung der Elemente oder ggf. Einschalten weicherer Elemente vor dem Verpreßkörper
kann die Kraft-Verschiebungslinie des Ankers an Messdaten angepasst werden (siehe Dissertation Slominski,
IBF 2006).
5. Vorspannung auf 80% der endgültiger Kraft ist ein Erfahrungswert. Der Rest (20%) während des weiteren
Aushubs kommt dazu. Die Richtigkeit dieser Annahme läßt sich mit FE überprüfen. Dafür betrachten wir
z.B. einen vorgespannten Anker bei -3m gefolgt durch
einen Aushub bis -6m. Die danach fehlende Reaktion
aus dem Erdwiederlager von -3 bis -6 m wird durch
• Anker
• Reduktion des Erddrucks auf der aktiven Seite
• Erhöhung des Erdwiderstands auf der passiven
Seite unterhalb von -6m
u
Belastung
durch
Aushub
Belastung
durch
Aushub
EA1
EA2
EA1 EA
2
EA
A3
EA3
Abbildung 16: Infolge des Aushubs erhält der Anker ein Teil
der Belastung proportional zu seiner Steifigkeit, analog zu
zwei verspannt zusammengeschraubten I-Profilen die auseinander gezogen werden.
∗NODE OUTPUT
U
∗ELEMENT OUTPUT, p o s i t i o n=n o d e s
S, E
∗CONTACT OUTPUT
CSTRESS
∗end step
Im entsprechenden STEP wird die Aussteifung wieder addiert:
∗step , extrapolation=no , nlgeom , INC=100000
S c h r i t t −3 = Einbau e i n e r ( v o r g e s p a n n t e n ? ) A u s s t e i f u n g
∗static , d i r e c t
1 ,1
∗model change , type=element , ADD=s t r a i n f r e e
Aussteifung
∗CONTROLS, ANALYSIS=DISCONTINUOUS
∗OUTPUT, FIELD , FREQUENCY=2
∗NODE OUTPUT
U
∗ELEMENT OUTPUT, p o s i t i o n=n o d e s
S, E
∗end step
Die vorgespannte Aussteifung definieren wir unter Anfangsbedingung
∗ i n i t i a l conditions , type=s t r e s s
A u s s t e i f u n g , −1.0E4
Hätten wir diese vorgespannte Aussteifung so eingebaut,
dann würde die Vorspannung zum Teil abgebaut. Es ist
Abbildung 17: Verpresskörper
durch die Verformung des Bodens und der Steife verursacht
die nach dem Einbau stattfindet. Um den Abbau der Vorspannung zu verhindern wird eine der Vorspannung entspreersetzt. Wie viel von dieser Kraft der Anker bekommt chende Kraft vor dem Einbau der Aussteifung in das Modell
hängt vom Verhältnis der drei Steifigkeiten da die aufgebracht
Bewegung der Wand als gemeinsam gesehen werden
∗CLOAD
kann.
13011 , 1 , 4 . 0 E2
Vorgespannte Steifen
dann die Steife mit
∗model change , type=element , ADD=s t r a i n f r e e
Aussteifung
1. Steifen können entweder als Federn (1 oder 2 KnotenElemente), Stäbe mit (EA) oder Balken (EAI) model- einbauen und danach, zusammen mit dem Loslassen der
liert werden.
Knoten (schon mit der Aussteifung)
2. Vorspannung funktioniert außer bei 1 Knoten-Federn ∗CLOAD
ähnlich wie bei Ankern. Aufbringen einer Einzellast 13011 , 1 , 0 . 0
und anschließendes Fixieren des freien Endes!!! Vorsicht bei der Wahl der Entsprechenden Federsteifigkeit Eine so eingeleitete Vorspannung bleibt erhalten, Abb. 18.
k bei Ausnutzung von Axialsymmetrie: nur die Hälfte Bei anschließender Belastung, z.B. bei einer Fortsetzung des
der tatsächlichen Steifenlänge soll als L in k = EA/L Aushubs, kann sich die Kraft in der Aussteifung frei ändern.
berücksichtigt werden.
Es macht Sinn, den Aushub schichtweise zu simulieren. Nach 2.11 Beispiel (ohne Wasser, ohne Kontakeinem Teilaushub kann ein Element (oder El.Gruppe) z.B.
te, ohne Steife)
Austeifung oder Anker, zum Modell mit
*model change, type=element, ADD=strain free
addiert werden. Dies ist aber nur dann möglich wenn das Modell einer Baugrube und die Berechnung des Aushubs
Element vorher entfernt wurde. Deshalb muss die Ausstei- ∗HEADING
l i t t l e −−e x c a v a t i o n
fung im Modell definiert und gleich im ersten Schritt *geostatic
∗NODE
entfernt werden.
1 ,0 ,0
∗ i n i t i a l conditions , type s t r e s s , g e o s t a t i c
....
∗ i n i t i a l conditions , type s t r e s s
A u s s t e i f u n g , −1000.0
.....
∗step
S c h r i t t −1 = g e o s t a t i s c h e s e q u i l i b r i u m
∗geostatic
∗dload
a l l e A B C e l e m e n t e , grav , 10 , 0 , −1 , 0
elemOK , P3 , 5
∗model change , type=element , remove
Aussteifung
∗CONTROLS, ANALYSIS=DISCONTINUOUS
∗OUTPUT, FIELD , FREQUENCY=2
31 , 15 , 0
∗NGEN, NSET=unten
1 , 31 , 1
∗NODE
3001 , 0 , 15
3031 , 15 , 15
∗NGEN,NSET=oben ,
3001 , 3031 , 1
∗NSET,NSET=b a l k e n k n o t e n ,GENERATE
1411 , 3011 , 100
∗NFILL ,NSET=a l l e k n o t e n
unten , oben , 30 , 100
∗NSET,NSET=l i n k s ,GENERATE
1 , 3001 , 100
∗NSET,NSET=r e c h t s ,GENERATE
Abbildung 18: Vorgespannte Anker: die Simulation der Einbaumethode ohne Abbau der Vorspannungskraft. Slomiński,
Diss. IBF Heft 169.
31 , 3031 , 100
∗ELEMENT, TYPE=CPE4
1 , 1 , 2 , 102 , 101
∗ELGEN,ELSET=a l l e
1 , 30 , 1 , 1 , 30 , 100 , 100
∗ELSET , ELSET=elemok ,GENERATE
2901 , 2930 , 1
∗ELSET ,ELSET=aushub1 ,GENERATE
2901 , 2910 , 1
∗ELSET ,ELSET=aushub2 ,GENERATE
2801 , 2810 , 1
∗ELSET ,ELSET=aushub3 ,GENERATE
2701 , 2710 , 1
∗ELSET ,ELSET=aushub4 ,GENERATE
2601 , 2610 , 1
∗ELSET ,ELSET=aushub5 ,GENERATE
2501 , 2510 , 1
∗ELSET ,ELSET=aushub6 ,GENERATE
2401 , 2410 , 1
∗ELSET ,ELSET=aushub7 ,GENERATE
2301 , 2310 , 1
∗ELSET ,ELSET=aushub8 ,GENERATE
2201 , 2210 , 1
∗ELSET ,ELSET=aushub9 ,GENERATE
2101 , 2110 , 1
∗ELSET ,ELSET=aushub10 ,GENERATE
2001 , 2010 , 1
∗ELEMENT, TYPE=B21
5001 , 1411 , 1511
∗ELGEN,ELSET=b a l k e n
5001 , 15 , 100 , 1
∗∗ −−−−−−−−−−−−−−−−−−−−−
∗∗
∗SOLID SECTION, ELSET=a l l e , MATERIAL=sand
∗MATERIAL, NAME=sand
∗ELASTIC
1 0 . E3 , 0 . 2 5
∗DENSITY
2.0
∗∗−−−−−−−−−−−−−−−−−−−−−
∗∗
∗BEAM GENERAL SECTION, SECTION=GENERAL, ELSET=b a l k e n
1 . 0 6 E−02 , 9 . 6 8 E−06 , , , , ,
0 , 0 ,−1
2 . 1 E+08 , 8 . 2 E+07
∗∗−−−−−−−−−−−−−−−−−−−−−
∗PREPRINT, ECHO=YES, CONTACT=YES, MODEL=YES
∗∗−−−−−−−−−−−−−−−−−−−−−
∗∗
∗∗ e f f e k t i v e spannungen
∗∗
∗BOUNDARY
unten , 2 , 2
links ,1 ,1
rechts ,1 ,1
∗INITIAL CONDITIONS, TYPE=STRESS , GEOSTATIC
a l l e , −5.0 , 15 , −305.0 , 0 . 0 , 0 . 5
∗∗==========STEPS==========
∗STEP
∗GEOSTATIC
∗DLOAD
a l l e , GRAV, 10 , 0 , −1 , 0
elemok , P3 , 5
∗CONTROLS, ANALYSIS=DISCONTINUOUS
∗OUTPUT, FIELD , FREQUENCY=2
∗NODE OUTPUT
U
∗ELEMENT OUTPUT, POSITION=NODES
S, E
∗END STEP
∗∗===========================
∗STEP , NLGEOM
1 . aushub : e l e m e n t e l o e s c h e n
∗STATIC , DIRECT
1 ,1
∗BOUNDARY, FIXED
alleknoten ,1 ,2
∗MODEL CHANGE, TYPE=ELEMENT, REMOVE
aushub1
aushub2
aushub3
aushub4
aushub5
aushub6
aushub7
aushub8
aushub9
aushub10
∗END STEP
∗∗============================
∗STEP , EXTRAPOLATION=NO, NLGEOM, INC=100000
1 . k n o t e n an n e u e r o b e r f l a e c h e l o e s e n
∗STATIC
0.001 , 1.0 , 0.0001 , 0.1
∗BOUNDARY, OP=NEW
links , 1 , 1
rechts , 1 , 1
unten , 2 , 2
∗NODE OUTPUT
U
∗ELEMENT OUTPUT
S, E
∗END STEP
2.12
Kritisches Betrachten der Ergebnisse
Gebrauchstauglichkeit (Verformungen, Verschiebungen) sieht
man direkt in Ergebnissen aber Verlust der Tragfähigkeit
(bei einer Last-Steuerung) zeigt sich nur als ein Problem bei
der Gleichgewichtsiteration. Die Berechnung wird abgebrochen mit der Begründung, dass die Konvergenz zu langsam
3.2
Materialbeschreibung für die Konsolidierungsberechnung
Neben des Stoffgesetzes und der Dichte braucht Abaqus die
Durchlässigkeit die in Abhängigkeit von der Porenzahl tabellarisch vorgegeben werden können.
*MATERIAL, NAME=name
...
*PERMEABILITY, TYPE=ISOTROPIC, SPECIFIC=10.0
k1 , e1
k2 , e2
...
mit den Durchlässigkeiten ki und den Porenzahlen ei (zu beachten: ei+1 ≥ ei ). Die Durchlässigkeit k ist ISOTROPIC und
die Wichte von Porenflüssigkeit ist SPECIFIC=10.0 kN/m3
Zum Beispiel
Abbildung 19: Verschiebungen infolge des Aushubs (elastisch).
ist oder sogar dass die Lösung numerisch divergiert. Das ist
kein Fehler im Programm sondern das Versagen des Materials. Bei einer Weg-Steuerung kann man sowohl die Peakals auch die Restfestigkeit (Verhalten nach dem Versagen)
des Systems untersuchen.
Die Tragfähigkeit eines FE Problems kann man mit einem
kinematischen Mechanismen überprüfen, z.B. mit dem Mathematica Programm LittleKEM.m
1. Parameter cu und φu = 0
2. Wichte ρ (mit Wasser ohne Auftrieb)
3. Mit der Tiefe zunehmendes cu , da die Poranzahl e
kleiner wird
4. Mechanismus mit einer Hebung der Sohle nicht vergessen. Ohne Kontaktelemente an der Wand kann der
Mechanismus nicht auftreten.
3
Aushub mit Konsolidierung
Der Porenwasserdruck wird wie eine weitere Knotenvariable
R
durch Abaqus
behandelt. Sie entspricht dem Freiheitsgrad DOF8 (DOF1...3 = Verschiebungen DOF4...6 = Rotationen der Knoten). Der Freiheitsgrad DOF8 wird nur
dort aktiviert, wo die speziellen Konsolidierungselemente
benutzt werden.
3.1
Konsolidierungselemente
Für 2D Probleme bietet Abaqus:
CPE4P, CPE4PH, CPE4RP, CPE4RPH, CPE6.., CPE8..
und für 3D Probleme:
C3D8P, C3D8PH, C3D8RP, C3D8RPH, C3D10.., C3D20..
mit PWD als Freiheitsgrad5 DOF8 an allen oder nur an den
Eckknoten.
5 2-D Elemente (DOF1, 2, 8 at corner nodes 1, 2 at midside nodes for
all elements except CPE6MP and CPE6MPH, which also have degree
of freedom 8 active at midside nodes)
3-D Elemente (DOF1, 2, 3 at midside nodes for all elements except
C3D10MP and C3D10MPH, which also have degree of freedom 8 active
at midside nodes 1, 2, 3, 8 at corner nodes)
∗SOLID SECTION, ELSET=e l e m g r u p p e , MATERIAL=sand
∗MATERIAL, NAME=sand
∗ELASTIC
1 0 . E3 , 0 . 2 5
∗DENSITY
2.0
∗PERMEABILITY,TYPE=ISOTROPIC ,SPECIFIC=1 0 . 0
2 . E−5 ,
0.7
2 . E−4 ,
1.2
3.3
Undränierter Fall (grob)
1. Der hohe Kompressionsmodul → 2.2GPa! führt bei
gewöhnlichen Elementen z.B. CPE4 zu volumetric locR
king. Jedoch das von Abaqus
zur Verfügung gestellte CPE4 Element verwendet die selektiv reduzierte
Integration (default).
2. Vereinfachte Methode via Steifigkeitsmatrix des Materials (z.B. ν = 12 ) setzt ideal undränierte Bedingungen
voraus.
Konsolidierungsanalyse ist aufwendiger und erfordert:
1. Spezielle Elemente z.B. CPE4P oder CPE8P
2. Spezieller gekoppelte Berechnungen bei Lösung des
RWPs, mit Verschiebungen und dem Porenwasserdruck
als Knotenwariablen (unbekannte Felder) z.B.
∗STEP ,AMPLITUDE=RAMP
∗SOILS , CONSOLIDATION
3.4
Stoffgesetze
1. Eine elastische Berechnung (fehlt Begrenzung des Spannungsverhältnisses (zu Fest und i.d.R. zu steif)) ist
nützlich um eine untere Grenze der Verformung zu
stellen und um die Geometrie des Modells so wie den
Ablauf der Berechnung zu überprüfen.
2. Mohr Coulomb / D-P / M-N (fehlt Dilatanz/Kontraktanz → sehr gefährlich, Skempton A,B)
3. Cam clay (Achtung auf die überhöhten K0 -Werte.
Akkumulation der Baugrubenwand-Verschiebung infolge einer zyklischen Belastung, z.B. infolge einer starken Vibration, wird nicht berücksichtigt)
4. Viskohypoplastizität (evtl. hysteretisch mit iD) iD nötig
für die Setzungsprognosen für benachbarte Gebäuden
5. Mögliche Schwierigkeiten bei zyklischer Beanspruchung Im Laufe der Berechnung kann sich die Porenzahl e infolge
der volumetrischen Verformung ändern.
• Aufbau des Porenwasserdrucks (Tragfähigkeit, proAnfangsporenwasserdrücke p(x) definiert man als Feld
gressiver Bruch)
• Akkumulation der Verformung (Gebrauchstauglichkeit)
• Mehrflächenmodelle notwendig
• Berechnung mit konventionellen und hochzyklischen Modellen möglich
∗INITIAL CONDITIONS, TYPE=PORE PRESSURE
EckKnoten1, p1 [, x1i , p2 , x2i ]
EckKnoten2, p1 [, x1i , p2 , x2i ]
...
Es ist zu beachten, dass bei CPE8P nur die Eckknoten den
Porenwaserdruck als DOF8 beinhalten. Nur die Eckknoten
werden deshalb mit EckKnotenGruppe angesprochen (sonst
R
6. Small-strain stiffness (Übergang dynamische - stati- Warnung von Abaqus
).
sche Steifigkeit wichtig für die Verformungsprognose,
besonders bei Verformmungsarmen Stützbauwerken. Anfangssättigungsgrade: definiert man die mit
Edyn /Estat ≈ 5)
∗INITIAL CONDITIONS, TYPE=SATURATION
EckKnoten1, Sr1 [, x1i , Sr2 , x2i ]
EckKnoten2, Sr1 [, x1i , Sr2 , x2i ]
3.5 AB für die Konsolidierungsberechnung . . .
und evtl. eine Abhängigkeit zwischen der Sättigung und dem
Anfangsporenzahlen und Anfangsspannung
PWD mit dem Befehl
Die Anfangsporenzahl definiert man mit
∗SORPTION,TYPE=ABSORPTION ,LAW=TABULAR
(1)
∗INITIAL CONDITIONS, TYPE=RATIO
EckKnotenGruppe1, e1 [, x1i , e2 , x2i ]
EckKnotenGruppe2, e1 [, x1i , e2 , x2i ]
p(1) , Sr
(2)
p(2) , Sr
(3)
p(3) , Sr
...
und die effektive Anfangsspannung (Kompression negativ) . . .
wodurch die Abhängigkeit Sr (p) tabellarisch definiert wurdefiniert man mit
de. Für p > 0 (Kompression im Wasser) werden wir i.d.R.
∗INITIAL CONDITIONS; TYPE=STRESS ,GEOSTATIC
Sr = 1 setzen.
(1)
(1)
(2)
(2)
ElemGruppe1, σ22 , x2 , σ22 , x2 , K0
Soll eine Teilsättigung berücksichtigt werden soll, definiert
(1)
(1)
(2)
(2)
ElemGruppe2, σ22 , x2 , σ22 , x2 , K0
man neben *SORPTION,TYPE=ABSORPTION analog auch:
...
*SORPTION,TYPE=EXSORPTION und
*SORPTION,TYPE=SCANNING In dem Beispiel verwenden wir
Bei Bestimmung der Anfangsspannung σ 0 (x, t = 0) muss keine *SORPTION Definitionen.
die Anfangsporenzahl e(x, t=0) berücksichtigt werden, weil
*DENSITY in der Materialdefinition als ρd verstanden wird.
Die effektive Spannung errechnet sich aus der Wichte γ 0 unter Auftrieb. Die Wichte unter Auftrieb berechnet Abaqus
unter Verwendung der Porenzahl e (initialisiert mit RATIO)
und der *DICHTE die als γd interpretiert wird.
3.6
Mehr Flexibilität via USER
Die Anfangsfelder lassen sich mit Fortran Routinen initialisieren, die durch Abaqus automatisch kompiliert und zum
Hauptprogramm gelinkt werden.
Beispiel:
Beispiele:
Eine Sandsäule zwischen x2 = 0 und x2 = 9 m habe Trocken3
wichte γd = 15 kN/m , Porenzahl e = 1.0, Porenanteil n = ∗INITIAL CONDITIONS, TYPE=STRESS , USER
e/(1 + e) = 0.5. Die Kornwichte ist γs = γd /(1 − n) = 30.0 bewirkt den Aufruf der externen subroutine SIGINI(....)
kN/m3 und die Auftriebswichte ist γ 0 = (1 − n)(γs − γw ) = die die Spannung initialisiert.
10 kN/m3 . Im geostatischen und hydrostatischen Zustand
ergibt sich daraus die effektive Spannung z.B.
∗INITIAL CONDITIONS, TYPE=SOLUTION, USER
∗INITIAL CONDITIONS; TYPE=STRESS ,GEOSTATIC
ElemGruppe,
-90,
0.0,
0.0 , 9.0 ,
0.5
Und bei der Materialbeschreibung setzen wir die Dichte
∗SOLID SECTION, ELSET=e l e m g r u p p e , MATERIAL=sand
∗MATERIAL, NAME=sand
∗ELASTIC
1 0 . E3 , 0 . 2 5
∗DENSITY
2.0
∗PERMEABILITY,TYPE=ISOTROPIC ,SPECIFIC=1 . 0
2 . E−5 ,
0.7
2 . E−4 ,
1.2
und schalten wir die Gravitation ein
∗STEP
∗GEOSTATIC
∗DLOAD
ElemGruppe , GRAV, 10 , 0 , −1 , 0
bewirkt den Aufruf der externen subroutine SDVINI(....)
womit die die vom Stoffgesetz gelesene Zustandsgrößen6 initialisiert werden.
∗INITIAL CONDITIONS, TYPE=PORE PRESSURE, USER
bewirkt den Aufruf der externen subroutine UPOREP(....)
die den Porenwasserdruck initialisiert.
∗INITIAL CONDITIONS, TYPE=RATIO, USER
bewirkt den Aufruf der externen subroutine VOIDRI(....)
die die Porenzahl initialisiert.
6 Manchmal wird so eine ’private’ Porenzahl für internen Gebrauch
im Stoffgesetz definiert. Eine solche Porenzahl ist mit den Gauss Punkten verknüpft und muss nicht identisch mit der Porenzahl RATIO (eine
Knoten-Variable) sein.
3.7
RB für Wasser
Dem Freiheitsgrad DOF8 (PWD nur an den Eckknoten)
müssen die RB am Anfang der Berechnung oder innerhalb
eines *STEPs zugewiesen werden (in alten Abaqus Versionen
RB für DOF8 nur in *STEPs). Ein undurchlässiger Rand
lässt sich nicht definieren7 , d.h. die Undurchlässigkeit ergibt sich aus der Topologie (z.B. die angrenzenden Elemente sind CPE8 und nicht mehr CPE8P), wenn man dort keine Dirichlet’sche RB definiert (kein Druck vorgibt). Eine Flussdichte 6= 0 lässt sich nicht definieren. Die Eckknoten, die sich im ’Inneren’ eines mit CPE8P bestückten Bereichs befinden, sind immer durchlässig 8 Am geometrischen
Rand9 wird entweder ein Porenwasserdruck p festgelegt (via
DOF8) oder eine Undurchlässigkeit vorausgesetzt (und p ergibt sich aus der Berechnung).
Im nachfolgenden Beispiel werden wir den ”trockenen” Bereich oberhalb des GWSpiegels mit CPE4- und den ”nassen” Bereich mit CPE4P-Elementen modellieren10 . An der
Wasserspiegeloberfläche (engl. phreatic surface) definieren
wir deshalb eine RB mit dem Wasserdruck p = 0 ohne Kapillarität.
∗STEP ,NLGEOM,AMP=RAMP
∗SOILS , CONSOLIDATION, END=PERIOD ,UTOL= 0 . 1
∆t0 , tEnde , ∆tmin , ∆tmax , ṗmin
führt eine instationäre Berechnungen der Wasserströmung
(mit Konsolidierung) aus.
Automatische Zeitschrittsteuerung:
• Sie basiert auf der erlaubten maximalen Änderung
des Porendrucks an einem Punkt während eines Inkrements.
• Der dem UTOL zugewiesene Wert 0.1 gibt, bei einer
instationaren Berechnung, die Hohe der maximal erlaubten Porendruckänderung pro Zeitinkrement an.
R
• Abaqus
begrenzt die Zeitschritte so, daß dieser Wert,
außer bei festgehaltenen Knoten, nicht überschritten
wird.
• Bei einer stationären Berechnung kann UTOL irgendein Wert ungleich Null zugewiesen werde. Die automatische Zeitsteuerung ist dann eingeschalten.
Ist die Spundwand durch einen Balken ohne Kontaktelemente modelliert (so wie im Modell ohne Wasser), kann Wasser Fehlt der Parameter UTOL werden die festgelegten Zeitschritte verwendet und die automatische Zeitsteuerung bleibt ausdurch eine solche Wand Widerstandsfrei fließen.
geschaltet
3.8
Berechnung
Sowohl bei Sickerströmung als auch bei der Konsolidierungsanalyse ist die Steifigkeit unsymmetrisch und daher Parameter UNSYMM=YES wird per Default in *SOILS-Berechnungen
verwendet, z.B.
∗STEP ,UNSYMM=YES
∗SOILS
∆t0 , tEnde , ∆tmin , ∆tmax
Der Aufruf eines STEPS mit:
∗STEP
∗SOILS
Die Abbruchskriterien für die STEP-Berechnung sind
• STEP-Zeit11 t > tEnde wird der Konsolidierungsprozess
• das Erreichen des stationären Zustands SS (engl. steaR
dy state) Ein ṗmin Kriterium definiert, was Abaqus
als ”stationär” akzeptieren soll (??)
• ...
Der Integrationsvorgang von ABAQUS stellt eine Beziehung
zwischen dem minimalen(!) verfügbaren Zeitinkrement ∆t
und der Elementgroße L her.
ohne Parameter CONSOLIDATION setzt stationäres Wasserγw 2
fließen voraus. Bei den Berechnungen wird zugrundegelegt,
∆t >
L ,
wobei
(5)
6Ek
daß die Zeit ausreicht, um instationäre Effekte vernachlässigen
zu können. Stationarität betrifft nur die Sickerströmung und
bei Stoffgesetzen (z.B. beim Kriechen) wird tEnde von *STEP γw die Wichte der Porenflussigkeit, E der Steifigkeitsmodul
des Bodens, k der Durchlassigkeitskoeffizient des Bodens ist.
berücksichtigt.
Wenn Zeitschritte kleiner als dieser Wert werden, können
Der Aufruf
nummerische Oszillationen der Lösung auftreten.
∗STEP ,NLGEOM,AMP=RAMP
∗SOILS , CONSOLIDATION,END=SS
∆t0 , tEnde , ∆tmin , ∆tmax , ṗmin
oder
7 Vergl.
stationäre Sickerströmmung, Num. in der Geot., Vorlesung
6.
8 vorausgesetzt
die Durchlässigkeit (*PERMEABILITY) der dortigen
Elemente > 0 ist.
9 In der FEM darf man generell die Verschiebungs- oder BelastungsRB an beliebigen Knoten definieren, auch in der Mitte eines diskretisierten Bereichs. Topologisch gesehen liegt also der Rand am jeden
Knoten. Per default wird überall die Knotenlast als Null angesetzt.
”Geometrischer” Rand eines CPE4P Bereichs entspricht dagegen einem Außenrand des Modells oder einer CPE4P-CPE4-Grenze.
10 Ein Versuch den trockenen Bereich mit CPE4P-Elementen zu modellieren mit Sr = 0 und mit der AB und RB p = 0 ergibt einen
R
Fehler. Die Anfangswichte wird durch Abaqus trotz Sr = 0 zu γ 0 ,
also mit Auftrieb (!!), ausgewertet.
Änderungen von Lasten und Randbedingungen während eines Berechnungsvorgangs sollten im selben Schritt definiert
und mit geeigneten Amplitudendefinitionen *AMPLITUDE für
deren Zeitverlauf versehen werden. Wenn Lasten und Randbedingungen fur diesen Schritt ohne die Option *AMPLITUDE
angegeben wird, benutzt ABAQUS den Wert des Parameters *AMPLITUDE in der Option *STEP, bzw. die Voreinstellungen.
∗HEADING
l i t t l e −−e x c a v a t i o n
∗NODE
1 ,0 ,0
31 , 15 , 0
∗NODE,NSET=w i d e r l a g e r F u e r S t e i f e
9000 , 0 , 15
∗NGEN
1 , 31 , 1
∗NSET,NSET=unten ,GENERATE
1 , 31 , 1
∗NODE
11 Im
Abaqus gibt es noch die globale Zeit
3001 , 0 , 15
3031 , 15 , 15
∗NGEN
3001 , 3031 , 1
∗NSET,NSET=oben ,GENERATE
3001 , 3031 , 1
∗NSET,NSET=b a l k e n k n o t e n ,GENERATE
1411 , 3011 , 100
∗NFILL ,NSET=a l l e k n o t e n
UNTEN,OBEN , 30 , 100
∗NSET,NSET=l i n k s ,GENERATE
1 , 3001 , 100
∗NSET,NSET=r e c h t s ,GENERATE
31 , 3031 , 100
∗NSET,NSET=t r o c k e n e k n o t e n ,GENERATE
1901 , 1931 , 1
2001 , 2031 , 1
2101 , 2131 , 1
2201 , 2231 , 1
2301 , 2331 , 1
2401 , 2431 , 1
2501 , 2531 , 1
2601 , 2631 , 1
2701 , 2731 , 1
2801 , 2831 , 1
2901 , 2931 , 1
3001 , 3031 , 1
∗NSET,NSET=n a s s e k n o t e n ,GENERATE
1,
31 , 1
101 ,
131 , 1
201 ,
231 , 1
301 ,
331 , 1
401 ,
431 , 1
501 ,
531 , 1
601 ,
631 , 1
701 ,
731 , 1
801 ,
831 , 1
901 ,
931 , 1
1001 ,
1031 , 1
1101 ,
1131 , 1
1201 ,
1231 , 1
1301 ,
1331 , 1
1401 ,
1431 , 1
1501 ,
1531 , 1
1601 ,
1631 , 1
1701 ,
1731 , 1
1701 ,
1731 , 1
1801 ,
1831 , 1
∗NSET,NSET=g w s p i e g e l k n o t e n ,GENERATE
1801 ,
1831 , 1
∗ELEMENT, TYPE=CPE4P
1 , 1 , 2 , 102 , 101
∗ELGEN,ELSET=n a s s e b o d e n e l e m e n t e
1 , 30 , 1 , 1 , 18 , 100 , 100
∗ELEMENT, TYPE=CPE4
1801 , 1801 , 1802 , 1902 , 1901
∗ELGEN,ELSET=t r o c k e n e b o d e n e l e m e n t e
1801 , 30 , 1 , 1 , 12 , 100 , 100
∗ELSET , ELSET=a l l e b o d e n e l e m e n t e
trockenebodenelemente , nassebodenelemente
∗ELSET , ELSET=elemok ,GENERATE
2901 , 2930 , 1
∗ELSET ,ELSET=aushub1 ,GENERATE
2901 , 2910 , 1
∗ELSET ,ELSET=aushub2 ,GENERATE
2801 , 2810 , 1
∗ELSET ,ELSET=aushub3 ,GENERATE
2701 , 2710 , 1
∗ELSET ,ELSET=aushub4 ,GENERATE
2601 , 2610 , 1
∗ELSET ,ELSET=aushub5 ,GENERATE
2501 , 2510 , 1
∗ELSET ,ELSET=aushub6 ,GENERATE
2401 , 2410 , 1
∗ELSET ,ELSET=aushub7 ,GENERATE
2301 , 2310 , 1
∗ELSET ,ELSET=aushub8 ,GENERATE
2201 , 2210 , 1
∗ELSET ,ELSET=aushub9 ,GENERATE
2101 , 2110 , 1
∗ELSET ,ELSET=aushub10 ,GENERATE
2001 , 2010 , 1
∗ELSET ,ELSET=t r o c k e n e b o d e n e l e m e n t e ,GENERATE
1801 , 1830 , 1
1901 , 1930 , 1
2001 , 2030 , 1
2101 , 2130 , 1
2201 , 2230 , 1
2301 , 2330 , 1
2401 , 2430 , 1
2501 , 2530 , 1
2601 , 2630 , 1
2701 , 2730 , 1
2801 , 2830 , 1
2901 , 2930 , 1
∗ELSET ,ELSET=n a s s e b o d e n e l e m e n t e ,GENERATE
1,
30 , 1
101 ,
130 , 1
201 ,
230 , 1
301 ,
330 , 1
401 ,
430 , 1
501 ,
530 , 1
601 ,
630 , 1
701 ,
730 , 1
801 ,
830 , 1
901 ,
930 , 1
1001 ,
1030 , 1
1101 ,
1130 , 1
1201 ,
1230 , 1
1301 ,
1330 , 1
1401 ,
1430 , 1
1501 ,
1530 , 1
1601 ,
1630 , 1
1701 ,
1730 , 1
1701 ,
1730 , 1
∗ELEMENT, TYPE=B21
5001 , 1411 , 1511
∗ELGEN,ELSET=b a l k e n
5001 , 16 , 100 , 1
∗∗ ∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗∗
SPRING
∗∗∗∗∗∗∗∗∗∗∗
∗ELEMENT, TYPE=SPRING2 , ELSET=a u s s t e i f u n g
6001 , 9000 , 3011
∗∗=================MATRIALS===========
∗SOLID SECTION, ELSET=t r o c k e n e b o d e n e l e m e n t e ,
MATERIAL=t r o c k e n e r s a n d
∗MATERIAL, NAME=t r o c k e n e r s a n d
∗ELASTIC
1 0 . E3 , 0 . 0
∗DENSITY
1.5
∗SOLID SECTION, ELSET=n a s s e b o d e n e l e m e n t e ,
MATERIAL=n a s s e r s a n d
∗MATERIAL, NAME=n a s s e r s a n d
∗ELASTIC
1 0 . E3 , 0 . 0
∗DENSITY
1.5
∗PERMEABILITY,TYPE=ISOTROPIC ,SPECIFIC=1 0 . 0
2 . E−5 ,
0.7
2 . E−4 ,
1.2
∗BEAM GENERAL SECTION, SECTION=GENERAL, ELSET=b a l k e n
1 . 0 6 E−02 , 9 . 6 8 E−06 , , , , ,
0 , 0 ,−1
2 . 1 E+04 , 8 . 2 E+04
∗∗ 2 . 1 E+08 , 8 . 2 E+07
∗SPRING, ELSET=a u s s t e i f u n g
1, 1
1E6
∗PREPRINT, ECHO=YES, CONTACT=YES, MODEL=YES
∗∗−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
∗∗
∗BOUNDARY
unten , 2 , 2
links ,1 ,1
rechts ,1 ,1
∗∗================INITIAL CONDITIONS=========
∗INITIAL CONDITIONS, TYPE=RATIO
ALLEKNOTEN , 1 . 0
∗INITIAL CONDITIONS, TYPE=SATURATION
nasseknoten , 1.0
∗INITIAL CONDITIONS, TYPE=PORE PRESSURE
nasseknoten ,
90.0 ,
0.0 ,
0.0 ,
9.0
∗INITIAL CONDITIONS, TYPE=STRESS , GEOSTATIC
trockenebodenelemente ,
−5.0 , 15 , −95.0 , 9 . 0 , 0 . 5
n a s s e b o d e n e l e m e n t e , −95.0 , 9 , −185.0 , 0 . 0 , 0 . 5
∗∗
herleitung :
−185 = −5 − 6 ∗15 − 9 ∗10
∗∗
mit $ \gamma d$=15 und $ \gamma ’ $=10 und f l ä c h e n l a s t=5
∗∗=================STEPS=====================
∗STEP
∗GEOSTATIC
∗DLOAD
ALLEBODENELEMENTE , GRAV, 10 , 0 , −1 , 0
elemok , P3 , 5
∗MODEL CHANGE, TYPE=ELEMENT, REMOVE
aussteifung
∗BOUNDARY
trockeneknoten ,8 ,8
gwspiegelknoten ,8 ,8
∗CONTROLS, ANALYSIS=DISCONTINUOUS
∗OUTPUT, FIELD , FREQUENCY=2
∗NODE OUTPUT
U
∗ELEMENT OUTPUT, POSITION=NODES
S , E ,POR , SAT
∗END STEP
∗∗============================================
∗STEP
1 . aushub : e l e m e n t e l o e s c h e n
∗STATIC , DIRECT
1 ,1
∗BOUNDARY, FIXED
ALLEKNOTEN , 1 , 2
9000 , 1 , 2
∗MODEL CHANGE, TYPE=ELEMENT, REMOVE
aushub1
∗END STEP
∗∗===========================================
∗STEP , EXTRAPOLATION=NO, NLGEOM, INC=100000
einbau e i n e r vorgespannten a u s s t e i f u n g
∗STATIC , DIRECT
1 ,1
∗MODEL CHANGE, TYPE=ELEMENT, ADD=STRAIN FREE
aussteifung
∗CLOAD
9000 , 1 , 1 0 0 . 0
∗CONTROLS, ANALYSIS=DISCONTINUOUS
∗OUTPUT, FIELD , FREQUENCY=2
∗NODE OUTPUT
U
∗ELEMENT OUTPUT, POSITION=NODES
S, E
∗END STEP
∗∗=========================================
∗STEP , EXTRAPOLATION=NO, NLGEOM, INC=100000
1 . k n o t e n an n e u e r o b e r f l a e c h e l o e s e n
∗STATIC
0.001 , 1.0 , 0.0001 , 0.1
∗BOUNDARY, OP=NEW
links , 1 , 1
rechts , 1 , 1
unten , 2 , 2
9000 , 1 , 2
∗CONTROLS, ANALYSIS=DISCONTINUOUS
∗OUTPUT, FIELD , FREQUENCY=2
∗NODE OUTPUT
U
∗ELEMENT OUTPUT, POSITION=NODES
S, E
∗END STEP
∗∗==========================================
∗STEP , NLGEOM
1 . aushub : e l e m e n t e l o e s c h e n
∗STATIC , DIRECT
1 ,1
∗BOUNDARY, FIXED
alleknoten ,1 ,2
9000 , 1 , 2
∗MODEL CHANGE, TYPE=ELEMENT, REMOVE
aushub2
aushub3
aushub4
aushub5
aushub6
aushub7
aushub8
aushub9
aushub10
∗END STEP
∗∗=========================================
∗STEP , NLGEOM, AMPLITUDE=RAMP
1 . KNOTEN AN NEUER OBERFLAECHE LOESEN
∗SOILS , UTOL=0 . 1
0.001 , 1.0 , 0.0001 , 0.1
∗BOUNDARY, OP=NEW
links , 1 , 1
rechts , 1 , 1
unten , 2 , 2
9000 , 1 , 2
∗CONTROLS, ANALYSIS=DISCONTINUOUS
∗OUTPUT, FIELD , FREQUENCY=2
∗NODE OUTPUT
U
∗ELEMENT OUTPUT, POSITION=NODES
S, E
∗∗∗ELEMENT OUTPUT, ELSET=a u s s t e i f u n g
∗∗ S11
∗END STEP