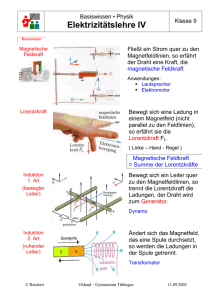
Bewegte Ladungen in Feldern

Bewegte Ladungen in Feldern
Elektronen verhalten sich in verschiedenen Feldern anders! In einem homogenen
elektrischen Feld verläuft die Flugbahn eines Elektrons, das senkrecht in das Feld
eintritt parabelförmig. Elektronen werden entgegengesetzt zur Feldrichtung
abgelenkt, da sie aufgrund ihrer negativen Ladung zum +-Pol gezogen werden. Man
kann dabei die Flugbahn in zwei Richtungen unterteilen, in x-Richtung und in yRichtung! Hierbei gilt:
In x-Richtung bewegt sich das Elektron mit:
s x =v⋅t
In y-Richtung bewegt das Elektron sich mit:
1
s y = ⋅a⋅t² ,dabei gilt
2
F =m⋅a mit
F =E⋅e
also: E⋅e=m⋅a
⇔a=
E⋅e
m
es ergibt sich:
1
⋅E⋅e
2
s y=
⋅t²
m
Bei der Berechnung der Flugbahn kann die Gravitationskraft außer acht gelassen
werden, da diese bei der sehr geringen Masse eines Elektrons extrem schwach ist!
Die Flugbahn eines Elektrons in einem Magnetfeld bildet hingegen eine Kreisbahn
oder einen Kreisausschnitt, da die magnetischen Feldlinien zu jedem Zeitpunkt
senkrecht zur Bewegungsrichtung sind, weil die Richtung der Lorentzkraft sich mit
dem Elektronenfluss ändert. Hierbei gilt Lorentzkraft=Zentripetalkraft F L =F Z
Warum Lorentz-Kraft?
Bei der Veranschaulichung der Lorentzkraft anhand der Leiterschaukel Tritt der Fall
ein, dass die Magnetfeldlinien auf der einen Seite sich verdichten, da jeder Strom
durchflossene Leiter ein Magnetfeld bildet, dessen Richtung man mit der
Linkenhand-Regel ermitteln kann, dies führt ebenfalls dazu, dass die
Magnetfeldlinien auf der anderen Seite weniger werden. Dieser Effekt führt dazu,
dass die Leiterschaukel von dem stärkeren Magnetfeld (in der Abbildung links vom
Leiter) weggedrückt wird. Dies passiert so lange bis die Gewichtskraft größer als die
Lorentzkraft wird. Dann bewegt sich der Leiter zurück und wir anschließend wieder
von der Lorentzkraft weggedrückt!
Die Richtung der Lorentzkraft kann mit der Drei-Finger-Regel der linken Hand
ermittelt werden.
Exkurs: Funktionsweise einer Photovoltaik-Anlage, Halbleiter, p- und n-dotierte
Halbleiter
→ http://www.planet-schule.de/sf/multimedia-interaktiveanimationen-detail.php?projekt=solarzelle