4. Klassenarbeit Mathematik 7b - hubert

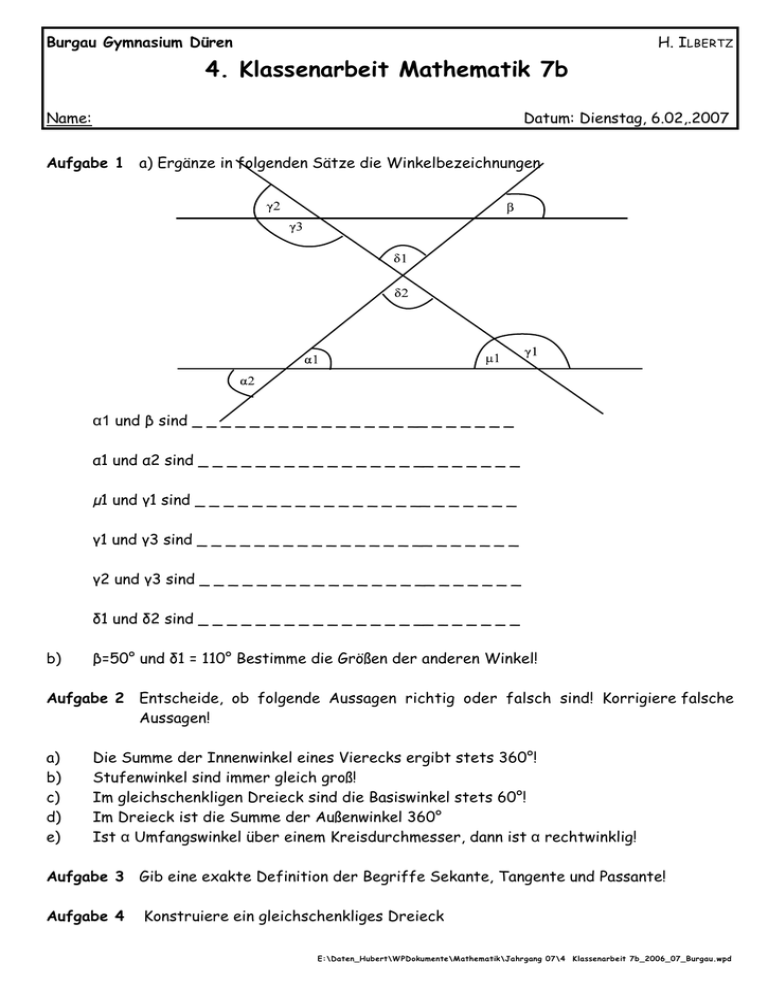
Burgau Gymnasium Düren
H. ILBERTZ
4. Klassenarbeit Mathematik 7b
Name:
Datum: Dienstag, 6.02,.2007
Aufgabe 1 a) Ergänze in folgenden Sätze die Winkelbezeichnungen
α1 und β sind _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ __ _ _ _ _ _ _
α1 und α2 sind _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ __ _ _ _ _ _ _
µ1 und γ1 sind _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ __ _ _ _ _ _ _
γ1 und γ3 sind _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ __ _ _ _ _ _ _
γ2 und γ3 sind _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ __ _ _ _ _ _ _
δ1 und δ2 sind _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ __ _ _ _ _ _ _
b)
β=50° und δ1 = 110° Bestimme die Größen der anderen Winkel!
Aufgabe 2 Entscheide, ob folgende Aussagen richtig oder falsch sind! Korrigiere falsche
Aussagen!
a)
b)
c)
d)
e)
Die Summe der Innenwinkel eines Vierecks ergibt stets 360°!
Stufenwinkel sind immer gleich groß!
Im gleichschenkligen Dreieck sind die Basiswinkel stets 60°!
Im Dreieck ist die Summe der Außenwinkel 360°
Ist α Umfangswinkel über einem Kreisdurchmesser, dann ist α rechtwinklig!
Aufgabe 3 Gib eine exakte Definition der Begriffe Sekante, Tangente und Passante!
Aufgabe 4
Konstruiere ein gleichschenkliges Dreieck
E:\Daten_Hubert\WPDokumente\Mathematik\Jahrgang 07\4 Klassenarbeit 7b_2006_07_Burgau.wpd
4. Klassenarbeit Mathematik 7b
Seite 2
mit folgenden Maßen: a = b= 6cm und γ=35°
Aufgabe 5
Nenne den Satz des Thales und beweise ihn mit
Hilfe einer Skizze, ohne den Mittelpunktswinkelsatz zu benutzen!
Aufgabe 6 Bestimme die Größen der Winkel und
begründe deine Angaben!
Aufgabe 7 In einer alten Schatzkarte des einäugigen Piraten Johnny Holzbein. heißt
es. Auf der Insel Takatuka stehen
zwei einsame Palmen. Ich habe in einem Umkreis von 30m um die
größere Palme einen wertvollen Schatz vergraben. Vom Punkt des
Schatzes aus sieht man die Palmen unter einem rechten Winkel!
Suche den Schatz durch geometrische Konstruktion. Alle Konstruktionslinien müssen sichtbar sein! Wähle als Maßstab 1cm ^
= 10m Beschreibe dein
Vorgehen!
Bonne chance!
E:\Daten_Hubert\WPDokumente\Mathematik\Jahrgang 07\4 Klassenarbeit 7b_2006_07_Burgau.wpd