Beispielaufgaben aus der zentralen Klassenarbeit Mathematik

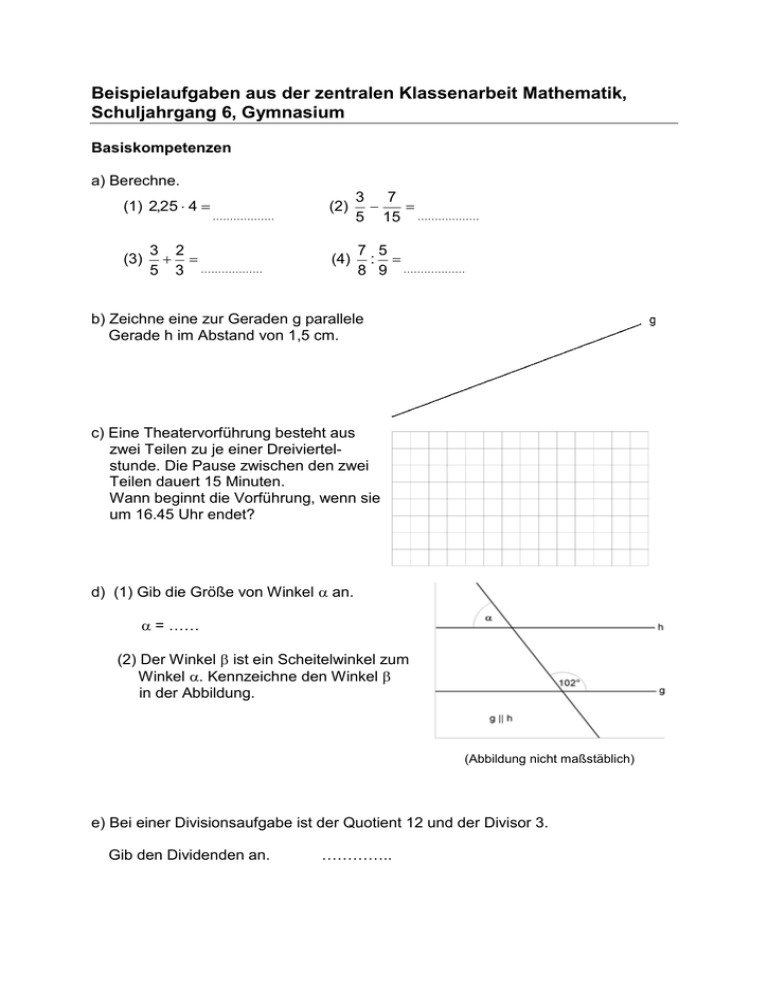
Beispielaufgaben aus der zentralen Klassenarbeit Mathematik,
Schuljahrgang 6, Gymnasium
Basiskompetenzen
a) Berechne.
(1) 2,25  4 
(3)
………………
3 2
 
5 3 ………………
(2)
3 7


5 15 ………………
(4)
7 5
: 
8 9 ………………
b) Zeichne eine zur Geraden g parallele
Gerade h im Abstand von 1,5 cm.
c) Eine Theatervorführung besteht aus
zwei Teilen zu je einer Dreiviertelstunde. Die Pause zwischen den zwei
Teilen dauert 15 Minuten.
Wann beginnt die Vorführung, wenn sie
um 16.45 Uhr endet?
d) (1) Gib die Größe von Winkel  an.
 = ……
(2) Der Winkel  ist ein Scheitelwinkel zum
Winkel . Kennzeichne den Winkel 
in der Abbildung.
(Abbildung nicht maßstäblich)
e) Bei einer Divisionsaufgabe ist der Quotient 12 und der Divisor 3.
Gib den Dividenden an.
…………..
Geometrie – Länge, Fläche und Volumen
a) Kira hat für einen Vortrag über Längen, Flächen und Volumen folgende Beispiele
aufgeschrieben. Sie hat bei der Zuordnung der Maßeinheiten einen Fehler
gemacht.
Korrigiere die falsche Maßeinheit.
(1) Länge eines Blumenkastens:
(2) Wohnfläche im Kinderzimmer:
(3) Wassermenge in einem Pool:
(4) Rasenfläche eines Sportplatzes:
1m
18 m³
150 m³
300 m²
b) Justin kann den 1,20 m langen und 60 cm breiten Schreibtisch seiner Tante für
sein Zimmer bekommen. Er möchte den Schreibtisch an eine Wand stellen ohne
das Zimmer umräumen zu müssen.
Zeichne in die gegebene Abbildung eine Möglichkeit ein, wie er den Schreibtisch
stellen kann.
c) Die Talsperre Wendefurth dient unter anderem dem Schutz vor Hochwasser.
In dem Stausee der Talsperre befinden sich rund 8 400 000 m³ Wasser. Die
Hälfte des Wassers soll an einem Tag abgelassen werden. Dabei fließen in einer
Minute 4 200 m³ Wasser aus dem Stausee.
Überprüfe durch eine Rechnung, ob die Hälfte des Wassers des Stausees an
einem Tag abgelassen werden kann.
Geometrie – Dreieck
Planfigur
1. Von einem Dreieck ABC sind gegeben:
a = BC = 6,0 cm
c = AB = 4,5 cm
 = ∢BAC = 80°
a) Fertige eine Planfigur an.
b) Konstruiere das Dreieck ABC.
c) Lisa behauptet, dass der folgende Kongruenzsatz für diese Konstruktionsdurchführung gilt.
Zwei Dreiecke sind zueinander kongruent, wenn sie in zwei Seiten und dem
eingeschlossenen Winkel übereinstimmen.
Entscheide, ob Lisa Recht hat und begründe deine Entscheidung.
2. Von einem gleichschenkligen Dreieck ABC sind die folgenden Stücke bekannt:
Länge der Basis:
Winkel an der Spitze:
Länge der Höhe:
c = 7,0 cm
 = 80°
hc = 4,0 cm
a) Berechne den Flächeninhalt des Dreiecks ABC.
b) Berechne die Größe eines Basiswinkels.
c) Nur eine der folgenden Seitenlängen ist die Schenkellänge des gegebenen
gleichschenkligen Dreiecks.
Kreuze diese Seitenlänge an und begründe deine Entscheidung.




b = 5,3 cm
b = 7,0 cm
b = 7,6 cm
b = 8,0 cm
Begründung
................................................................................................................................
................................................................................................................................
................................................................................................................................
Stochastik – Datenauswertung
1. Eine Klassenarbeit der Klasse 6a hat folgendes Ergebnis:
Zensur
Anzahl
1
3
2
4
3
10
4
6
5
2
6
0
a) Berechne den Durchschnitt der Klassenarbeit.
b) Paul und Tina waren krank und müssen die Klassenarbeit nachschreiben.
Sie erhalten die Zensuren 2 und 4.
Ändert sich der Durchschnitt der Klassenarbeit? Begründe deine Antwort.
c) Die Klasse 6b erreichte bei dieser Klassenarbeit folgendes Ergebnis:
Zensur
Anzahl
1
6
2
8
3
10
4
2
5
2
6
0
Der Durchschnitt der Klassenarbeit beträgt 2,5.
Max und Elias haben die Klassenarbeit nachgeschrieben. Der Durchschnitt
dieser Klassenarbeit hat sich dadurch nicht geändert.
Welche Zensuren könnten Max und Elias erhalten haben?
Zensur von Max:
………
Zensur von Elias: ………
2. Mario findet auf einem Notenblatt die folgende Melodie:
a) Er möchte wissen, wie viele Noten mit welchen Notenwerten es in dieser Melodie
gibt.
Stelle die jeweilige Anzahl fest und vervollständige folgende Tabelle.
Notenwerte
Anzahl
Ganze Noten
Halbe Noten
Viertel Noten
Achtel Noten
b) Veranschauliche die Anzahl der jeweiligen Notenwerte in einem Diagramm.
Stochastik – Tabellen
In der folgenden Tabelle sind Angaben zu den neun
Nachbarstaaten der Bundesrepublik Deutschland
zusammengestellt.
Nachbarstaat
Belgien
Dänemark
Frankreich
Luxemburg
Niederlande
Österreich
Polen
Schweiz
Tschechische Republik
Länge der
Grenze zu
Deutschland
in km
156
67
448
135
567
815
442
316
811
Fläche des
Landes
in km2
Anzahl der
Einwohner
in 1000
30 518
43 096
543 965
2 586
41 864
83 853
312 683
41 293
78 864
10 708
5 493
62 277
489
16 645
8 337
38 126
7 648
10 424
a) Gib an, wie viele Einwohner Frankreich hat. …………..................................
b) Tim sagt: „Je kleiner die Fläche eines Nachbarstaates ist, desto kürzer ist seine
Grenze zu Deutschland.“
Was meinst du dazu? Begründe.
c) Vergleiche die Bevölkerungsdichte (Anzahl der Einwohner pro km²) der
Niederlande mit der Bevölkerungsdichte der Schweiz. Setze das richtige Zeichen
(<; =; >) und begründe.
Bevölkerungsdichte der Niederlande
.……...
Bevölkerungsdichte der Schweiz
……….
Begründung: