17. Wärme und erster Hauptsatz

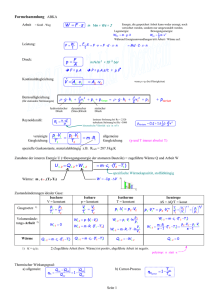
03.04.2014
17. Wärme und erster Hauptsatz
17.1 Wärmekapazität C
Wärme war historisch schwer vorstellbar (Transport, ohne Materie ?). Modell: „Calorikum“
bis Mitte 19. Jahrh.
Was ist Wärme ?
Eine Form der Energie: Die Energie, die von einem System auf ein
Anderes aufgrund einer Temperatur-Differenz übertragen wird.
keine eigenständige physikalische Größe, sondern nur eine gleichwertige Form von Energie,
wie z.B. die mechanische.
Einheit: Wärme Q [Joule] [J], (historisch Kalorie [cal])
Beispiel: Abschrecken eines heißen Stahls in kaltem Wasser
Q
T1
T2
heisser Stahl
T1 > T2 
kaltes Wasser
Im selben System oder 2 Systeme in Kontakt: Temperaturausgleich
bis ein thermisches Gleichgewicht erreicht ist, d.h. T1 = T2
Körper 1 gibt Wärmemenge Q1 ab und kühlt dadurch ab; Körper 2 nimmt die Wärmemenge
Q2 auf und erwärmt sich: Es muß gelten (Energieerhaltung): Q1 = Q2 = Q
Ausgleich über: Wärmeleitung, -strahlung oder Konvektion (siehe 17.8)
Welche Wärmemenge Q muss zu- / abgeführt werden um ein ΔT zu erzielen?
Q  C  T
vgl. elektrisch:
Q  C  
C Wärmekapazität
mit Massetransport verbunden
bei Wärme auch ohne Stofftransport möglich

elektrisches Potential
17-1
03.04.2014
Bezogen auf die Masse:
Q  c  m  T
mit
c
C
m
spezifische Wärme (-kapazität)
Beispiel:
cW  4,17
1 kg H2O; ΔT = 0°C auf 100°C;
kJ
kg  K
Q  1 kg  4,17
kJ
 100 K  417 kJ
kg  K
Welche Masse mCu muß ein Kupferblock mit T = 500°C besitzen, um 1 kg H2O von 0°C auf
100°C zu erwärmen? Die gemeinsame Endtemperatur beträgt T = 100°C. cCu  0,382
Q
417
kJ  kg  K

 2,73 kg
cCu  T 0,382  400 kJ  K
mCu 
T  400C  400 K
kJ
kg  K
Molare Wärmekapazität, bezogen auf 1 Mol, d.h. konst. Teilchenzahl
Wichtig:
cm  M  c
M Molmasse
C  n  cm
für n  Mol
c wird entweder bei konst. Druck (cp) oder konst. Volumen (cv) bestimmt.
Eine Temperaturänderung hat vor allem bei Gasen auch eine Änderung des
Drucks bzw. des Volumens zur Folge.
Meisten Körper: Volumenausdehnung für T 
Q

T

aber auch
V
d.h. c p  cv
mechanische Arbeit (siehe 17.5)
für V = const.:
nur T
für P = const.:
V  const : V und T, d.h. T ist kleiner als für V = const.
 mit Q = geg. und c p 
Q
T
17-2
 cp 
03.04.2014
Für Festkörper und Flüssigkeit:
c p  cv geringe Volumenausdehnung (siehe 15.4.2)
Für Gase :
c p  cv
Tab.17.1: Wärmekapazitäten fester Stoffe bei 20°C und flüssiger Stoffe bei 25°C.
cp / J kg-1 K-1
Stoff
Beryllium
C (Graphit)
C (Diamant)
Aluminium
Eisen
Kupfer
Zink
Molybdän
Silber
Gold
Blei
Al2 O3
SiO2(Quarz)
CaF2
KCl
Benzol (C6 H5 OH)
Äthanol (C2 H5 OH)
Methanol (CH3 OH)
Quecksilber
Wasser
H2O:
1750
676
502
888
452
382
387
251
235
129
129
764
745
868
682
1740
2420
2550
140
4170
cp / J mol-1 K-1
15,80
8,12
6,03
24,00
25,20
24,30
25,30
24,10
25,30
25,40
26,80
77,20
44,76
67,70
50,80
135,90
111,50
81,71
28,10
75,12
sehr großes c : d.h. die pro kg gespeicherte Energie ist sehr groß  Wärmespeicher
 Milderung von Temperturschwankungen am Meer (Meeresklima)
c ist meist = f (T), für H2O jedoch sehr konstant. Nachteil: TDampf niedrig.
Tab. 17.2: Spezifische Wärmekapazitäten von Gasen bei 25°C und 1 bar.
Stoff
He
Ar
Kr
Xe
H2
Cl2
N2
O2
CO2
cp [J/(kg K)]
5233
523
248
160
14300
473
1041
917
837
cp [J/(mol K)]
cv [J/(mol K)] cp / cv
20,95
20,90
20,78
21,00
28,83
33,54
29,16
29,34
36,84
12,62
12,47
12,30
12,65
20,45
24,84
20,81
21,12
28,49
17-3
1,660
1,676
1,690
1,660
1,410
1,350
1,401
1,389
1,239
cp – cv [J/(mol K)]
8,33
8,43
8,48
8,35
8,38
8,70
8,35
8,22
8,35
03.04.2014
17.2 Latente Wärme, Umwandlungswärme
lat.: latere = verbergen
Versuch: Schmelzen von Lötzinn
reversibel
- Bereiche konstanter Temperatur trotz
dQ
 const (konstante Wärmezufuhr)
dt
- Wärme wird nicht zur Temp.- Erhöhung genutzt, sondern für Phasenübergänge
- Phasenübergänge: fest
 flüssig:
Schmelz-
energie

Erstarrungs-
energie
flüssig  gasförmig: Verdampfungs- energie

fest
QV [J/kg]
Kondensation- energie
 gasförmig: Sublimations- energie

Q  m  Qi
QS [J/kg]
QSub [J/kg]
Kondensations- energie
Qi materialspezifisch i: S, V, Sub
fest  flüssig  gasförmig: Steigender Abstand der Moleküle/Atome  Aufbrechen von
Bindungen
und
Überwinden
von
Anziehungskräften
(elektrisch). Keine Umwandlung der Wärme in kin.-Energie
(Temp.-Erhöhung) sondern pot.-Energie
17-4
03.04.2014
Tab. 17.3: Schmelzpunkte und Siedepunkte sowie Schmelzwärmen QS und Verdampfungs-
wärmen QV einiger Substanzen bei 103 mbar. (Die Werte für Kohlendioxid beziehen sich auf
die Sublimation, da flüssiges CO2 bei Atomsphärendruck nicht existent ist).
Substanz
Schmelzpunkt / K
Blei
Brom
Ethanol
Gold
Helium
Kohlendioxid
Kupfer
Quecksilber
Sauerstoff
Schwefel
Silber
Stickstoff
Wasser
Zink
600
266
159
1336
1356
234
54,4
388
1234
63
273,15
692
QS / kJ  kg-1
Siedepunkt / K QV / kJ  kg-1
24,7
67,4
109
62,8
205
11,3
13,8
38,5
105
25,7
333,5
102
2023
332
351
3081
4,2
194,6
2839
630
90,2
717,75
2436
77,35
373,15
1184
858
369
879
1701
21
573
4726
296
213
287
2323
199
2257
1768
Beispiel: 1 kg Eis von T = -20°C in Dampf (T = 100°C)
kJ
kg  K
-20°C  0°C:
c p  2,05
Q1  1 kg  2,05
fest  flüssig :
Schmelzwärme: QS = 333,5 kJ/kg
0°C  100 °C:
c p  4,17
flüssig  gas:
Verdampfungswärme: Qv  2257
Eis
kJ
 20K  41 kJ
kgK
Q2  m  Qs  333,5 kJ
kJ
kgK
Q3  1 kg  4,17  100K  417 kJ
kJ
kg
Q4  m  Qv  2257 kJ
Viel Energie für Phasenübergänge !
Hinweis:
Wasserkühlung durch Verdunsten: Schwitzen des Körpers, Nähe von
Gewässern, Spanische Tonkrüge, Ziegenschlauch
Kondensation an kalten Körpern: Abgabe von Wärme a. d. kühlere Medium
17-5
03.04.2014
17.3 Innere Energie U
Temperaturerhöhung eines Systems  Zufuhr von Wärme  höhere kin. Energie der
Teilchen (Atome, Moleküle)  höhere Energie des Systems. Das System bewegt sich
jedoch nicht. Wkin = 0.
Unterschied: Innere und äußere Energie
Äußere Energieformen Wa:
Translation
- Kinetische Energie Wkin
Rotation
- Potentielle Energie Wpot
z.B.: Bewegung einer Thermoskanne
Innere Energieformen Wi:
- thermische Energie (Wärme): Translation, Rotation,
Schwingungsenergie der Moleküle / Atome
(siehe kin.
Gastheorie)
- chemische Energie: potentielle Energie steckt in den
Bindungen: exotherm oder endotherm; Phasenübergänge
- nukleare Energie: Bindungsenergie im Kern: (Kernfusion,
-spaltung)
z.B.: heiße Flüssigkeit in einer Thermoskanne
System:
Wges  Wa  Wi
Wa  Wkin  W pot
mit Wi  U
innere Energie
U  Wges  Wa
U  f (T , P, V , m) = Zustandsgröße
wegunabhängig
17-6
03.04.2014
17.4 Erster Hauptsatz
Annahme zur Vereinfachung:
Geschlossenes System: Austausch von Wärme und Arbeit, kein Austausch von m
Beispiel: Joules Experiment
W Zufuhr von mechanischer Energie
Das Rühren erhöht T und damit U
Q
Wpot
Abgabe von Wärme (schlechte Isolation)
Regel: (aus der Sicht des Systems)
Zugeführte Energie:
positiv
Abgeführte Energie:
negativ
mit Wab  0 und Qab  0 :
Bilanz der Arbeit: W  Wzu  Wab
Bilanz der Wärme: Q  Qzu  Qab
Gesamtbilanz:
U  Wzu  Qzu  Wab  Qab  Q  W
1. Hauptsatz der Thermodynamik:
Satz von der Energieerhaltung
- Zufuhr:
Sowohl in Form von Q (siehe Kap. 17.1) als auch als W
- Im System: Alles wird als innere Energie U gespeichert, nicht als Wärme Q oder als
mechanische Energie W. Nicht mehr unterscheidbar.
U   Wkin  
n
 k T
2
als „Temperatur“ gespeichert
Annahme: ideales Gas, d.h. keine Chemie,
geringer Druck
n Anzahl der Freiheitsgrade (1-atomig: n=3)
- Abgabe:
U kann sowohl in Q oder W umgewandelt werden, hängt vom System ab.
17-7
03.04.2014
17.5 Volumenarbeit
Annahme: beweglicher, reibungsfreier Kolben, ideales Gas, m = const.
F  P A
mechanische Arbeit:
dW  F  dx  P  
A dx
dV
dW   P  dV
aus der Sicht des Systems:
Expansion:
dV > 0 Arbeit abgeben
dW < 0
Kompression: dV < 0 Arbeit aufnehmen dW > 0
Beispiel: Isotherme Expansion / Kompression
V2
W12    P (V )  dV
Expansion
V1
V1
W21    P (V )  dV
Kompression
V2
Beispiel: Isoth. Expansion ( d.h. W12 < 0): für T = const  mit U 
n
k  T  U = const.
2
mit Wzu = Qab = 0
ΔU = 0 = W12 + Qzu  W12 = Qzu 
Frage:
Zufuhr von Wärme für isotherme Expansion
wie groß ist Q12 auf dem Weg von 1 nach 2?
für ideales Gas:
P1  V1  P2  V2  n  R  T
n Anzahl der Mole!
3 mögliche Wege: Sind U12, Q12, W12 wegabhängig?
Alternativen
17-8
s.o.
03.04.2014
A) Weg 1:
Weg 2:
B) Weg 1:
Weg 2:
Prozeß
Abgegebene mechanische Energie W12
Erwärmen für P1 = const:
W1   P1 ( V2  V1 )
Isobare Expansion
Abkühlen für V = const:
W2  0
Isochore Abkühlung
Gesamt
W A   P1 (V2  V1 )
Abkühlen für V = const:
W1  0
Isochore Abkühlung
Erwärmen für P2 = const:
W2   P2 (V2  V1 )
Isobare Expansion
Gesamt
WB   P2 (V2  V1 )
dWC   P  dV  
C) Isotherme Expansion:
n  R T
dV
V
V2
1
V
dV   n  R  T ln 2
V
V1
V1
dWC   n  R  T 
Gesamt
Ergebnis: Unterschiedliche Wege  unterschiedliche Expansionsarbeit W12.
Endpunkte gleich heißt keine Temperaturänderung  gleiche innere Energie U.
U  Q  W  0

Q  W
Folgt: unterschiedlich zugeführte Wärmemengen: ΔQA > ΔQC > ΔQB (= Fläche ΔW)
W, Q keine Zustandsgrössen  ! Wegabhängig !
U
Zustandsgröße
 ! Wegunabhängig !
17.6 Adiabatische Zustandsänderung
Definition: Kein Austausch von Wärme mit der Umgebung (ideale Wärmeisolation).
Näherung für sehr schnelle Prozesse ohne Temperaturausgleich (dauert).
Q  0
U  Q  W
 U  W
die mechanische Arbeit (Expansion) wird durch Änderung der inneren Energie (d.h. T sinkt)
bereitgestellt und umgekehrt.
17-9
03.04.2014
 
cP
cV
P  V   const
Adiabatenkoeffizient
T  V  1  const
T
 const
P 1
Poisson Gleichungen
vgl:
Isotherme:
dT = 0  dU = 0
Isochore:
dV = 0  dW = 0
Isobare:
dP = 0
Adiabate:
dQ = 0  dW = dU
17.7 Kreisprozesse
Definition: geschlossener Umlauf  dU = 0 für ideales Gas
da T = const nach einem Umlauf:
(für ideales Gas wird U nur in Form von
T gespeichert)
z.B.: Ottomotor
(einfache Näherung)
a,c adiabatisch, d.h. dQ = 0
Wab
b, d isochor, d.h. dV = 0
ΔW insgesamt abgegebene Arbeit
Wzu
1. Rechtsläufig:
a) Expansion:
im Uhrzeiger im P-V Diagramm
Abgabe von Volumenarbeit:
c) Kompression: Zufuhr von Volumenarbeit
Wab  Wa    P dV  0
dV  0
Wzu  Wc    P dV  0
dV  0
Bilanz der mechanischen Arbeit ΔW = Wzu + Wab < 0 : mehr Abgabe als Aufnahme
17-10
03.04.2014
b) Abkühlung:
Qab < 0
Bilanz ΔQ > 0: mehr Wärmeaufnahme
d) Erwärmung: Qzu > 0
U  Wab  Wzu  Qab  Qzu  0
<0
2. Linksläufig:
>0
Bilanz: Arbeitsaufnahme und Wärmeabgabe
Beispiel: rechtsläufig:
linksläufig:
1. Hauptsatz
Wärmekraftmaschine: Motoren
Kältemaschine: Kühlschrank mit Kompressor
Wirkungsgrad W einer Wärmekraftmaschine (Motor):
W 
Nutzen
verrichtete Arbeit

Aufwand zugeführte Wärme
Aufwand = Qzu zugeführte Wärme;
insgesamt verrichtete Arbeit = W  Wzu  Wab
abgeführte Qab ist verloren für den Kreisprozess!
evtl. andere Nutzung (Kraft – Wärme Kopplung)
U  0 
W  Qzu  Qab
W  0
verrichtete Arbeit
aus der Sicht des Systems
W 
Qzu  Qab
Q
 1  ab
Qzu
Qzu
mit
Qab < 0
oder
W  1 
Qab
Qzu

W  1
W groß wenn Qab klein, d.h. kein Abkühlen
ohne Abkühlen (Qab = 0) aber kein sinnvoller Kreisprozeß möglich: für identischen Rückweg
 mechanische Arbeit mit W = 0).
d.h. W = 1 nicht möglich, d.h. nicht alle zugeführte Wärme Qzu wird in Arbeit W umgesetzt.
17-11
03.04.2014
Wärmereservoir zum Aufheizen (z.B. Benzin)
Wärmekraftmaschine
Kältereservoir zum Abkühlen (z.B. Kühler)
2. Hauptsatz:
Es gibt keine periodische Maschine, die Wärme vollständig in mechanische Arbeit
umsetzt. Stets gilt: ηW < 1
Idealfall: Carnot-Prozeß (Wärmekraftmaschine)
Vollständig reversibler Prozeß und idealisiert  maximal möglicher Wirkungsgrad, d.h.
ideale Maschine (geht nicht real) zur Abschätzung des Grenzfalles:
1-2:
isotherme Expansion dU = 0
QW   WW   P  dV  
 n  R  TW  ln
3-4:
n  R  TW
dV
V
V2
V1
isotherme Kompression dU = 0
 QK  WK    P  dV  n  R  TK  ln
2-3:
adiabatische Expansion dQ = 0:
mit T  V  1  const allgemein
TW  V2 1  TK  V3 1
TW  V3 
 
TK  V2 
17-12
 1
V3
V4
03.04.2014
4-1:
adiabatische Kompression dQ = 0:
TK  V4 1  TW  V1 1
TW  V4 
 
TK  V1 
 1
Carnot Wirkungsgrad für reversible Prozesse
mit W  1 
Qab
QZu

W max  1 
QK
T
 1 K
QW
TW
in [K] !
 = 1 nur für TK = 0 K: geht nicht (siehe Kap. 18.4.3: 3. Hauptsatz))
 groß für TK /TW klein
real:  real  Carnot  1
Ursache für nicht reversible Prozesse: z.B. Reibung, Turbulenzen, Nichtgleichgewicht
Beispiele:
Kohlekraftwerk
25 ... 50 %
Dampfmaschine
3 ... 44 %
Dieselmotor
bis 45 %
Ottomotor
bis 37 %
Elektromotor
20 ... 99,5 %
Elektromotor mit Strom aus Kohle: 0,5 · 0,9 = 0,45
Carnot Kältemaschine (ideale Kühlschrank, Klimaanlage):
an Umgebung
linksläufig: Wärme QK aus dem Bereich mit
niedrigerer TK (Kühlschrank innen) abführen
QW in einen Bereich höherer Temperatur TW
(Umgebung). Dazu muß Arbeit W verrichtet
werden (Kompressor).
aus Kühlraum
17-13
03.04.2014
Leistungszahl der Kältemaschine:
abgeführte Wärme QK

verrichtete Arbeit W
K 
abgeführte Wärme aus dem Kühlraum = zugeführte Wärme QK zum Kompressor
aus dU  0  W   QW  QK  0
K 
1
QK

QW  QK QW  1
QK
Für Carnot gilt (s.o.):
QW TW

QK TK
 K max 
TK
1

TW
 1 TW  TK
TK
Typ. Werte für einen Kühlschrank: ε  5
17.8 Wärmetransport
3 Arten: Wärmeleitung
Konvektion
Materie gebunden
ohne
Materietransport
Wärmestrahlung
ohne Materie
mit
Materietransport
nur
Energietransport
In der Praxis Mischung aus allen drei
Prinzip:
Wärme Q strömt immer längs eines Temperaturgefälles = negativer
Temperaturgradient
17-14
03.04.2014
17.8.1 Wärmeleitung
Definition: Materiegebundener Transport ohne Materietransport. Vorherrschend in
Festkörpern
TW  TK  T
T
 Temperaturgradient
x
Ausgleichsvorgang: Wärmestrom I 
dQ
bis TW  TK
dt
Thermodynamisches Gleichgewicht
Es fließt nur Energie keine Materie !
Annahme:
Stationärer Zustand oder Fließgleichgewicht:
d.h. große Reservoire
TW  const; TK  const
z.B. TW = geheizte Wohnung und TK = Umgebung
Physikalischer Mechanismus: Energieübertragung durch Atomstöße. In Metallen zusätzlich
Unterstützung durch frei bewegliche Ladungen
Beschreibung durch empirisches Gesetz:
Wärmestrom:
I
dQ
T
   A
dt
x
Stromdichte:
j
T
I

x
A
W
Q ist Wärme nicht elektr. Ladung
W
 m 2 
 W 
 spez. Wärmeleitfähigkeit 
 m  K 
17-15
03.04.2014
Tab. 17.4: Spezifische Wärmeleitfähigkeiten bei Raumtemperatur
Material
 W/(m·K)
Material
 W/(m·K)
Silber
428
Polyurethanschaum
0,024
Kupfer
400
Wasser
0,6
Stahl
14 - 40
Eis
0,59
Beton
0,19 – 1,3
menschl. Gewebe
0,2
Ziegel
0,84
Wolle
0,04
Holz
0,1 - 1
Daunen
0,025
Glas
0,7 – 0,9
Luft
0,023
 = (T) jedoch konstant für Metalle im Bereich 0°C < T < einige 100°C
im stationären Zustand gilt: I = const. ≠ f (t)
T  I 
damit:
R
Wärmewiderstand:
x
 I R
A
x
A
K
 W 
  U  I  R mit R 
vgl. elektrisch:
l
 A
Serienschaltung:
T1  T2  T3
1)
T1  T2  I  R1
2)
T2  T3  I  R2
1) + 2) T1  T3  I  R1  R2 
n
Rges  R1  R2  ...  Rn   Ri
i 1
Beispiel: Wärmedämmung
17-16
03.04.2014
Parallelschaltung:
n
1
1

Rges i 1 Ri
Beispiel: Thermographie Hausfront
dunkel: kalt, hohes R
hell: warm, kleines R
Haus: T1
1 Fenster
T2 aussen
2 Wand
RHolz > RZiegel > RFenster + Vorhang > RFenster. Dach schlecht isoliert
Frage: Warum ist die Sauna aus Holz und nicht aus Metall?
Hohe Wärmeleitfähigkeit von Metall führt schnell Wärme zu (fühlt sich heisser an),
Holz hat eine wesentlich niedrigere Leitfähigkeit. Metallische Gegenstände in der
Sauna können Verbrennungen hervorrufen. Aufguß erhöht die Leitfähigkeit der Luft,
„es wird wärmer“.
17.8.2 Konvektion
Definition: Mit Materietransport verbundener Wärmetransport. Vorherrschend in
Gasen und Flüssigkeiten.
Beispiele:
passive: Meeresströmung, Thermik
aktive: Ventilator
17-17
03.04.2014
Mathematische Beschreibung sehr komplex und nur näherungsweise möglich.
Wärmeübergang:
Randschichten an der Grenzfläche fest – gas
dort der größte Teil des Temperaturabfalls
hängt ab von der Strömungsgeschwindigkeit
Beispiele:
Glasfenster: Erhöhung von R um bis zu 45% je Seite mit vLuft = 0. d.h. das Glas
isoliert nur zu 10%
Doppelverglasung: optimaler Abstand zwischen den Scheiben ca. 1 – 2 cm,
sonst Konvektion; zusätzlich Vorhänge, Rollos reduzieren vLuft
Wind Chill Faktor
Vorteil von Daunen, Schäumen (kleine eingeschlossene Luftvolumen)
17.8.3 Wärmestrahlung
Definition: Braucht keine Materie. Reiner Energietransport durch elektromagnetische
Strahlung
Emission:
Abgestrahlte Leistung: Stefan – Boltzmann Gesetz
PE  e    A  T 4
e
Emissionsgrad (materialabhängig)

Stefan – Boltzmann Konstante = 5,67·10-8
A
abstrahlende effektive Fläche
T
Temp. des Körpers [K]
W
m  K4
Emission durch Elektronenübergänge im Festkörper
Absorption: Leistungsaufnahme aus der Umgebung
PA  e    A  T04
T0
Umgebungstemperatur [K]
Jeder Körper emittiert und absorbiert gleichzeitig:
T > T0
Emission überwiegt
T < T0
Absorption überwiegt

PN  e    A  T 4  T04
Nettostrahlungsleistung:
17-18

2
03.04.2014
Emissionsgrad:
e
gilt für Emission und Absorption. Jeder Körper emittiert und
absorbiert gleich gut.
e = 1:
schwarzer Strahler (Körper) oder idealer Strahler
e=0
sehr helle, reflektierende Oberflächen
e=
f (Wellenlänge )
Versuch: Strahlungswürfel
Heizen mit heißem Wasser; Messen mit Termoelement
4 Flächen : Spiegel / Metall matt / Heizkörperfarbe / Schwarze Farbe:
Meßwerte:
0,38
0,39
2,9
2,9 (gemessene Temp. nicht e)
Wellenlängenabhängigkeit für schwarze Strahler:
max
Wien’sche Verschiebungsgesetz:
max mm 
2,898
T K 
(Verteilungsfunktion u(, T) siehe Kap. 19)
Beispiele:
maximal sichtbare Wellenlänge  800 nm 
Abstrahlung
bei
kleiner
Temperatur
nicht
Tsichtbar > 500°C
sichtbar,
aber
meßbar
(Thermographie)
Körpertemperatur: T  33°C = 306 K
max  9,47 μm
e (9,47 μm)  1 unabhängig von Hautfarbe
d.h auch im sichtbaren Bereich nicht schwarze Strahler
können im IR-Bereich schwarze Strahler sein
17-19
03.04.2014
Blau:
kalt
schlecht durchblutet
Rot:
warm
gut durchblutet
vorher
Sonne:
nach einer Zigarette
max  500 nm  T  5800 K
Mitte des sichtbaren Spektralbereichs – Zufall ?
Abgestrahlte Leistung:
Pe  1350 J/(m2·s)
Klarer Tag:
PErde  1000 J/(m2·s)
Absorbierte Wärme:
Q
J
 1000 2  e  A  cos 
t
m s
Solarkonstante
Aeff  A  cos 
Jahreszeiten:
Aeff = f (Jahreszeit)
17-20