Anfänger-Praktikum I WS 11/12 Praktikumsbericht: Stoßgesetze

Anfänger-Praktikum I WS 11/12
Michael Seidling
Timo Raab
Praktikumsbericht: Stoßgesetze
1
Inhaltsverzeichnis
Inhaltsverzeichnis
I. Einführung
4
II. Grundlagen
4
1. Die Zykloide
4
2. Das Trägheitsmoment
5
3. Die Energie
3.1. Kinetische Energie . . .
3.1.1. Rotationsenergie
3.1.2. Bewegungsenergie
3.2. Potentielle Energie . . .
3.3. Energieerhaltungssatz . .
.
.
.
.
.
6
6
6
6
7
7
4. Der Impuls
4.1. Impulserhaltungssatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
8
5. Der Stoß
5.1. elastischer Stoß . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2. inelastischer Stoß . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
9
9
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
III. Versuch
10
1. Beschreibung
10
2. Aufbau
10
3. Durchführung
10
4. Messung
11
5. Auswertung
14
6. Fehlerbetrachtung
18
IV. Fragen
18
1. Frage 1: rotation von rollenden Kugeln
18
2
Inhaltsverzeichnis
V. Anhang
20
1. Abbildungs- und Tabellenverzeichnis
20
2. Quellen
20
3
1 DIE ZYKLOIDE
Teil I.
Einführung
Das Ziel dieses Versuchs ist, die Gesetzmäßigkeiten beim Zusammenstoß von zwei Kugeln
in zwei Dimensionen zu betrachten. Dabei überprüfen wir die Gültigkeit des Energieerhaltungssatzes, sowie des Impulserhaltungssatzes.
Teil II.
Grundlagen
Bei einem Stoß handelt es sich um die Wechselwirkung zwischen zwei Körpern, bzw. Teilchen. Um diesen Prozess beschreiben zu können benötigt man den Energieerhaltungssatz
der Mechanik, sowie den Impulserhaltungssatz. Des weiteren werden Zykloide, sowie das
Trägheitsmoment eine Rolle in der Betrachtung spielen.
1. Die Zykloide
Betrachtet man einen Punkt auf einem Kreis, der über eine Ebene rollt, beobachtet man
eine Zykloide.
Abbildung 1: Gewöhnliche Zykloide
Die Bahnkurve ~x(t) eines Kreises mit dem Radius r, lässt sich dann beschreiben:
x(t)
rt − r · cos(t)
~x(t) =
=
(1)
y(t)
r − r · sin(t)
Die besondere Eigenschaft der gewöhnlichen Zykloiden, die wir uns im Versuch zu
nutze machen, ist die Tautochronie. Wenn man die Reibung vernachlässigt und auf einer
umgekehrten Zykloide 2 Massenpunkte an unterschiedlichen Stellen gleichzeitig freigibt,
kommen sie gleichzeitig am unteren Ende an. Dabei haben sie aber eine unterschiedliche
Geschwindigkeiten. Der Grund dafür ist, dass es die Zykloidenbahn oben steiler ist und
so diese Kugel stärker beschleunigt wird wie eine Kugel, die nicht so nahe am oberen
Ende ist.
4
2 DAS TRÄGHEITSMOMENT
Abbildung 2: zwei Kugeln rollen von unterschiedlichen Startpositionen in dem selben
Zeitintervall an das Ende der Bahn
2. Das Trägheitsmoment
Das Trägheitsmoment J ist eine Größe, die die Masseverteilung in einem Körper beschreibt. Dabei spielt die Masse mi sowie der jeweilige Abstand ri von der Rotationsachse
ω durch den Schwerpunkt des Körpers ab:
X
J=
∆mi ri2
(2)
i
Betrachtet man infinitessimal kleine Massen ergibt sich für einen Körper mit konstanter
Dichte ρ das Trägheitsmoment:
Z
2
J = lim ∆mi ri = ρ ri2 dV
(3)
∆mi →∞
Bei einer Kugel mit dem Radius R und der Masse M erhält man:
2
J = M · R2
5
5
(4)
3 DIE ENERGIE
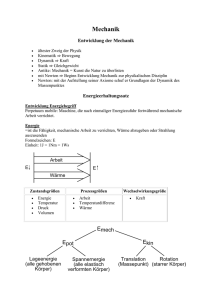
3. Die Energie
Die Energie ist eine nicht absolute mathematische Hilfsgröße. Sie beschreibt Zustände
eines Körpers im Vergleich zu einem frei wählbaren Nullniveau. Es gibt verschiedene
Arten von Energie. Diese können ineinander umgewandelt werden.
3.1. Kinetische Energie
Um einen Körper zu bewegen, muss eine Kraft auf ihn wirken, diese beschleunigt ihn nach
dem 1. Newtonschen Axiom F = ma. Es gibt zwei verschiedene Arten von kinetischer
Energie Ekin , Bewegungsenergie T und Rotationsenergie Erot :
Ekin = T + Erot
(5)
Allgemeiner kann man sagen, dass der Betrag des Bewegungszustandes p ausschlaggebend ist:
Ekin =
p2
2m
(6)
3.1.1. Rotationsenergie
Um einen Körper in Rotation zu versetzen, muss eine Kraft auf ihn wirken. Diese
Kraft verrichtet Arbeit, die als Rotationsenergie Erot gespeichert wird. Dabei spielt das
Trägheitsmoment J, sowie die Winkelgeschwindigkeit ω eine Rolle:
1
Erot = Jω 2
2
(7)
Bei einer Kugel mit dem Radius R und der Rollgeschwindigkeit vr gilt für die Winkelgeschwindigkeit ωr :
~ = ω~r · R
~ · sin π ⇔ ωr = vr
vr = |ω~r × R|
2
R
(8)
3.1.2. Bewegungsenergie
Um einen Körper in Bewegung zu versetzen, muss ihn eine Kraft auf ihn wirken. Diese
Kraft verrichtet Arbeit, die als Bewegungsenergie T gespeichert wird. Diese ist proportional zur Masse m des Körpers und hängt von dem Betrag der Geschwindigkeit |~v | = v
des Körpers ab.
1
T = mv 2
2
6
(9)
4 DER IMPULS
3.2. Potentielle Energie
Die potentielle Energie Epot , ist die Energie die in der Lage des Körpers gespeichert
ist. Zudem muss man sich in einem konservativen Kraftfeld befinden. Das heißt, dass
die Kraft F~ die auf den Körper wirkt nicht von der Geschwindigkeit v oder der Zeit t
abhängt. An einem bestimmten Ort ~r gilt für die Kraft:
F~(~r) ∗ ~r = −Epot(~r)
(10)
Wird ein Körper entlang eines Kraftvektors bewegt, gilt bei einer Bewegung von dem
Ort ~r1 zu dem Ort ~r2 :
∆Epot = Epot(~r2 ) − Epot(~r1 )
(11)
Da das Gravitationsfeld der Erde in der Nähe der Erdoberfläche nahezu ein konservatives Kraftfeld ist gilt für die Kraft F~ = m ∗ ~g , daraus ergibt sich für einen Körper der
Masse m der sich in der Höhe h über einem freigewählten Nullniveau befindet:
Epot = mgh
(12)
3.3. Energieerhaltungssatz
In einem geschlossenen System kann Energie nicht erschaffen“ werden oder verloren“
”
”
gehen. Das bedeutet die Gesamtenergie E ist zeitlich konstant. Mittels des Energieerhaltungssatzes der Punktmechanik, in der nur die potentielle Energie Epot und die kinetische
Energie Ekin eine Rolle spielt, kann man einge Probleme lösen.
E = Epot + Ekin = const.
(13)
4. Der Impuls
Der Impuls ist ein vektorielles Maß für den Bewegungszustand eines Körpers. Nach dem
1. Newtonschen Axiom ist der Impuls eines Körpers zeitlich kostant.Für den Impuls p~
eines Körpers mit der Masse m und der Geschwindigkeit ~v gilt:
p~ = m~v
(14)
Nach dem 2. Newtonschen Axiom ist eine Impulsänderung eines Körpers zwingend
mit dem wirken einer Kraft F~ verbunden, wobei wir die Masse des Körpers als zeitlich
konstant betrachten:
d~v
dm
d~p
= m + ~v
= m~a
(15)
F~ =
dt
dt
dt
|{z}
=0
7
4 DER IMPULS
Das 3. Newtonsche Axiom besagt, dass in einem geschlossenen System jede wirkende
Kraft F~w eine gleichgroße in Gegenrichtung gerichtete Kraft F~r bewirkt:
F~w = −F~r
(16)
Verbindet man nun die Glechungen (15) und (16) so erhält man:
pw d~pr
(15) d~
F~w + F~r = 0 ⇔
+
=0
dt
dt
Nach der Integration über die Zeit:
Z
Z
Z
d~pr
d~pw
dt +
dt = 0 dt
dt
dt
p~w + p~r = const.
(17)
(18)
4.1. Impulserhaltungssatz
Aus (18) folgt, das der Gesamtimpuls p~ in einem geschlossenen System konstant ist. Das
bedeutet, wenn zwei Körper in einem geschlossenen System in Wechselwirkung treten,
ist die Summe der Impulse p~1 und p~2 gleich zu der Summe der Impulse p~∗1 und p~∗2 danach:
p~ = p~1 + p~2 = p~∗1 + p~∗2 = const.
m1~v1 + m2~v2 = m1~v1∗ + m2~v2∗ = const.
8
(19)
(20)
5 DER STOSS
5. Der Stoß
Der Stoß ist eine Wechselwirkung zwischen zwei Teilchen oder Körpern. Es gibt zwei
Arten von Stößen, den elastischen und den inelastischen Stoß. In beiden Fällen handelt
es sich um ein geschlossenes System, indem keine Kraft von außerhalb wirkt. Somit
gilt der Impulserhaltungssatz und der Energieerhaltungssatz, die zum Beschreiben von
Stoßprozessen benutzt werden.
5.1. elastischer Stoß
Bei dieser Art von Stoß geht keine kinetische Energie von den Teilchen oder Körpern
verloren. Das bedeutete es sind idealisierte Bedingungen. Reibung spielt hier also keine
Rolle. Zudem darf keine Energie bei dem Stoß an sich verloren gehen, also der Körper
darf nach dem Stoß nicht deformiert sein.
∗
Ekin = Ekin
∗
∗
E1kin + E2kin = E1kin
+ E2kin
p2
p∗2
p∗2
p21
+ 2 = 1 + 2
2m1 2m2
2m1 2m2
(21)
(22)
5.2. inelastischer Stoß
Bei dem inelastischen Stoß wird ein Teil der kinetischen Energie, die vor dem Stoß
vorhanden war, in andere Energiearten umgewandelt. Beispielweise kann Energie zum
Verformen eines Körpers verwendet oder in Wärme umgewandelt werden. Dennoch gilt
der Impulserhaltungssatz und der Energieerhaltungssatz wird nicht verletzt.
∗
Ekin = Ekin
+W
9
(23)
3 DURCHFÜHRUNG
Teil III.
Versuch
1. Beschreibung
Der Versuch Stoßgesetze“ dient zur Überprüfung des Energieerhaltungssatzes und des
”
Impulserhaltungssatzes. In dem Versuch führen zwei Kugeln einen nahezu elastischen
Stoß aus.
2. Aufbau
Abbildung 3: Aufbau
Zwei Bahnen, die die Eigenschaft der Tauchatrie haben, werden so an die Tischkante gestellt, dass wenn die zwei Kugeln gleichzeitig freigegeben werden, sich in der Luft
treffen. Um das gleichzeitige freigeben zu gewährleisten, ist auf jeder Bahn ein Elektromagnet montiert, der verschoben werden kann, und die mit einem Schalter ein und
ausgeschaltet werden können. Deshalb müssen die Kugeln magnetisch sein. Auf dem Boden wird ein großes Papier ausgebreitet, sodass die Kugeln darauf landen. Desweiteren
wird ein Senklot benötigt, um die Tischkante sowie den Ort an dem sich die Kugeln
Stoßen auf dem Papier zu markieren.
3. Durchführung
Die beiden Kugeln werden gewogen und erhalten ihre Bahn. Es wird geprüft, ob sich
die Kugeln in der Luft treffen. Ist dies nicht der Fall, muss mithilfe von Papier, dass
zwischen einer Kugel und dem Elektromagneten plaziert wird, die Auslöszeit korrigiert
10
4 MESSUNG
werden.Der Ort des Zusammenstoßes wird mit Hilfe des Senklots markiert und beschriftet, ebenso wie die Position der Abwurfpunkte und der Tischkante. Ist alles markiert,
wird jede Kugel einzeln drei mal ihre Bahn heruntergerollt und der Auftreffort mithilfe
von Kohlepapier markiert. Dann werden beide Kugeln drei mal gleichzeitig gestartet
und ihre neuen Auftrefforte werden auf dem Blatt markiert. Das wiederholt man mit
geänderter Geschwindigkeit von einer Kugel, sowie einem geänderten Winkel der Bahn.
4. Messung
Für die Auswertung wurde ein Koordinatensystem angelegt. Damit können wir die Geschwindigkeit der Kugeln durch die Differenz berechnen. Für die Differenzkoordinaten
bei den Treffpunkten ist zu beachten, dass die erste Differenz die Strecke zwischen dem
jeweiligen Treffpunkt und der rechten Bahn ist, der zweite Wert steht für die Strecke
zwischen dem jeweiligen Treffpunkt und der linken Bahn. Außerdem haben wir von der
rechten Bahn immer die schwere Kugel starten lassen, von der linken immer die leichte.
mgr = 66, 8g
mkl = 43, 4g
(24)
(25)
Der Fehler für das Gewicht der Kugeln beträgt 5%.
Die Abwurfhöhe betrug immer (0, 781 ± 0, 001) m.
Für die Messungen standen die Bahnen in folgendem Verhältnis:
Messung 1 (*): Die Kugeln wurden von identischen Höhen losgelassen“
”
Messung 2 (#): Die Höhe der rechten Bahn, also der schweren Kugel wurde verringert
Messung 3 (@): Die Höhen wurden wie bei Messung 2 belassen, der Winkel zwischen
den Bahnen wurde vergrößert
Auf dem nachfolgenden Bild kann man die Auftreffpunkte auf dem Blatt und alle anderen wichtigen Punkte sehen. Die genauen Koordinaten kann man den darauffolgenden
Tabellen entnehmen. Unter Messrelevante Punkte fallen alle Punkte, die mit dem Lot
bestimmt wurden, also die Abwurfposition der Kugeln und ihre Treffpunkte bei gemeinsamen Würfen “.
”
Fehlerrechnung Da wir nicht genau messen konnten, da wir kein Lineal zur Verfügung
hatten, und es öfters ansetzen mussten mit einem Fehler von ca. 2%. Dieser Fehler setzt
sich in ∆x und ∆y dann fort1 :
δ∆ = δM essung1 + δM essung2
δM essung1
δM essung2
δ∆
=
+
|∆|
|M essung1| |M essung2|
1
Nach Fehlerrechnung des AP: (C.1.5)
11
(26)
(27)
4 MESSUNG
Beschriftung
Rechte Bahn
Linke Bahn Anfang
Treffpunkt *
x-Koordinate
-0,2
-0,15
3,65
y-Koordinate
25,65
19,95
22,8
K gem 1*
K gem 2*
K gem 3*
G gem 1*
G gem 2*
G gem 3*
G allein 1*
G allein 2*
G allein 3*
K allein 1*
K allein 2*
K allelin 3*
29,25
24,9
25,4
37,4
40,1
40,4
34,95
34,7
34,85
33,9
33,9
33,6
3,2
5,7
5,55
34,75
34
33,25
11,45
10,85
11,5
40,3
40,1
40,15
12
∆x
∆y
δx
δy
3,85 -2,85
3,8
2,85
25,6 -19,6 0,6 0,5
21,25 -17,1 0,5 0,5
21,75 -17,25 0,5 0,5
33,75 11,95 0,8 1,2
36,45 11,2 0,8 1,2
36,75 10,45 0,8 1,2
35,15 -14,2 0,7 1,2
34,9 -14,8 0,7 0,7
35,05 -14,15 0,7 0,7
34,05 20,35 0,7 0,7
34,05 20,15 0,7 0,7
33,75 20,2 0,7 0,7
4 MESSUNG
Beschriftung
Rechte Bahn
Linke Bahn Anfang
Treffpunkt #
x-Koordinate
-0,2
-0,15
1,8
y-Koordinate
25,65
19,95
22,5
K gem 1#
K gem 2#
K gem 3#
G gem 1#
G gem 2#
G gem 3#
G allein 1#
G allein 2#
G allein 3#
K allein 1#
K allein 2#
K allein 3#
41,25
40,2
40,5
19,3
20
19,8
23,5
23,5
23,3
33,6
34
34
13,7
13,9
13,9
32,75
32,6
33
16
16,3
16,05
41
40,6
40,35
Beschriftung
Rechte Bahn
Linke Bahn verändert
Treffpunkt @
x-Koordinate
-0,2
-0,25
1,9
y-Koordinate
25,65
21,4
23,8
K gem 1@
K gem 2@
K gem 3@
G gem 1@
G gem 2@
G gem 3@
G allein 1@
G allein 2@
G allein 3@
K allein 1@
K allein 2@
K allein 3@
39,9
37,7
37,55
21,9
23,15
23,55
23,5
23,6
23,7
37,4
37,25
37,7
11,35
10,05
10,7
30,75
31,5
31,55
16
15,7
15,85
35,45
36,1
35,2
13
∆x
∆y
δx
δy
2,0
-3,15
22,65 2,55
39,45 -8,8 0,8 0,7
38,4
-8,6 0,8 0,7
38,7
-8,6 0,8 0,7
17,5 10,25 0,4 1,2
18,2 10,1 0,4 1,2
18
10,5 0,4 1,2
23,7 -9,65 0,5 0,8
23,7 -9,35 0,5 0,8
23,5
-9,6 0,5 0,8
33,75 21,05 0,7 1,2
34,15 20,65 0,7 1,2
34,15 20,4 0,7 1,2
∆x
∆y
δx
δy
2,1
-1,85
2,15
2,4
38
-12,45 0,8 0,7
35,8 -13,75 0,8 0,6
35,65 -13,1 0,8 0,6
20
6,95 0,4 1,1
21,25
7,7
0,5 1,1
21,65 7,75 0,5 1,1
23,7 -9,65 0,5 0,8
23,8 -9,95 0,5 0,8
23,9
-9,8 0,5 0,8
37,65 14,05 0,8 1,1
37,5
14,7 0,8 1,2
37,95 13,8 0,8 1,1
5 AUSWERTUNG
5. Auswertung
Für den Fehler in unseren Abstandsmessungen nehmen wir einen Fehler von 2% an.
Es ist noch zu sagen, dass wir nur die Bewegungen in x- und y-Richtung betrachten.
Nach Gleichung (14) benötigen wir für die Berechnung des Impulses die Geschwindigkeit
der Kugeln.
Für die Geschwindigkeit benötigen wir zunächst die Zeit, die die Kugeln in der Luft
waren. Dafür verwenden wir als Formel:
r
1 2
2s
s = gt ⇒ t =
(28)
2
g
s ist hier nun unsere Abwurfhöhe aus Kapitel 4, also (0,781 ± 0,001)m.
g ist unsere Fallbeschleunigung. Für diese nehmen wir 9,81 sm2 an.
tGesamt = (0, 399s ± 0, 0001)s. 2
Nun werden zunächst die Einzelwürfe “ausgewertet. Hierfür bestimmen wir jeweils den
”
Mittelwert aus den 3 Würfen. Danach berechnen wir zunächst die Gesamtstrecke.
p
sGesamt = ∆x2 + ∆y 2
(29)
Mit diesen berechnen wir dann unsere Geschwindigkeiten mit der Formel:
v=
s
t
(30)
t ist in diesem Fall 0,399s. Dies wurde zuvor durch die Fallstrecke ermittelt.
Mit der Geschwindigkeit ermitteln wir dann unseren Impuls nach Gleichung (14).
Dies alles wird auf Grund der Übersicht in der folgenden Tabelle geschehen.
Die Strecken sind in cm angegeben, v in ms und der Impuls in kg ms .
Fehlerrechnung Der Fehler von ∆x und ∆y wird erst quadriert, dann addiert, und
daraus die Wurzel gezogen. Damit erhält man für (29):
δs
δx
δy
= 0, 5 · 2 ·
+2·
|s|
|∆x|
|∆y|
δx
δy
⇔ δs =
+·
· |s|
|∆x|
|∆y|
(31)
(32)
Für Gleichung (14) und (30) ergibt sich für den Fehler 3 :
δa
δb
δc
=
+
|a|
|∆b| |∆c|
14
(33)
5 AUSWERTUNG
Beschriftung
G allein 1*
G allein 2*
G allein 3*
K allein 1*
K allein 2*
K allein 3*
G allein 1#
G allein 2#
G allein 3#
K allein 1#
K allein 2#
K allein 3#
G allein 1@
G allein 2@
G allein 3@
K allein 1@
K allein 2@
K allein 3@
∆x
∆y
35,15 -14,2
34,9 -14,8
35,05 -14,15
34,05 20,35
34,05 20,15
33,75 20,2
23,7 -9,65
23,7 -9,35
23,5
-9,6
33,75 21,05
34,15 20,65
34,15 20,4
23,7 -9,65
23,8 -9,95
23,9
-9,8
37,65 14,05
37,5
14,7
37,95 13,8
MW ∆x
MW ∆y
sGesamt
δs
v
δv
p
35,18
-14,38
38,01
1,5
0,95 0,04
0,063 0,006
33,95
20,23
39,52
1,6
0,99 0,04
0,043 0,004
23,63
-9,53
25,48
1,1
0,64 0,03
0,043 0,004
34,02
20,70
39,82
1,6
1,00 0,04
0,043 0,004
23,80
-9,80
25,74
1,1
0,65 0,03
0,43
0,004
37,70
14,18
40,28
1,6
1,01 0,04
0,44
0,004
Für die gemeinsamen Würfe benötigen wir eine andere Zeit, um die Geschwindigkeit
nach dem Stoß zu ermitteln. Die Kugeln sind bei Stößen gleich lang unterwegs wie bei
Würfen ohne Stoß. Um die Zeit zwischen dem Abwurf und dem Stoß und der Gesamtzeit steht im gleichen Verhältnis wie die die Strecke zwischen Abwurf und Stoß und
Gesamtstrecke.
tAbwurf →Stoss
sAbwurf →Stoss
=
sGesamt
tGesamt
(34)
Dies muss für jede Kugel und für jeden Stoß einzeln bestimmt werden. Hierfür gilt dann:
tStoss→Boden = tGesamt − tAbwurf →Stoss
tStoss→Boden = tGesamt ∗ (1 −
sAbwurf →Stoss
)
sGesamt
(35)
(36)
Fehlerechnung Die Vererbung des Fehlers ist Identisch zu Gleichung (33).
Den Gesamtimpuls berchnen wir nun, indem wir bei den gemeinsamen Würfen die
Impulse betragsmäßig addieren.
pGesamt = pKugel1 + pKugel2
2
3
Nach Fehlerrechnung des AP: (C.1.8)
nach Fehlerrechnung des AP (C.15)
15
(37)
δp
5 AUSWERTUNG
Versuchsreihe
*
#
@
Beschriftung
K gem 1*
K gem 2*
K gem 3*
G gem 1*
G gem 2*
G gem 3*
K gem 1#
K gem 2#
K gem 3#
G gem 1#
G gem 2#
G gem 3#
K gem 1@
K gem 2@
K gem 3@
G gem 1@
G gem 2@
G gem 3@
Bahn
Rechts
Links
Rechts
Links
Rechts
Links
sGesamt
38,01
39,52
25,48
39,82
25,74
40,28
sAbwurf →Stoss
4,79
4,75
3,73
3,21
2,80
3,22
∆x
∆y
sGesamt
25,6 -19,6
32,24
21,25 -17,1
27,28
21,75 -17,25 27,76
33,75 11,95
35,80
36,45 11,2
38,13
36,75 10,45
38,21
39,45 -8,8
40,42
38,4
-8,6
39,35
38,7
-8,6
39,64
17,5 10,25
20,28
18,2
10,1
20,81
18,0
10,5
20,84
38,0 -12,45 39,99
35,8 -13,75 38,35
35,65 -13,1
37,98
20,0
6,95
21,17
21,25
7,7
22,60
21,65 7,75
23,00
Versuchsreihe
*
δs
1,3
1,1
1,1
1,4
1,5
1,5
1,6
1,6
1,6
0,8
0,8
0,8
0,8
1,5
1,5
0,8
0,9
0,9
pGesamt Einzeln δpEinzeln
0,106
0,010
0,086
0,008
0,087
0,008
#
*
16
tStoss→Boden
0,349
0,351
0,341
0,366
0,356
0,367
v
0,919
0,777
0,791
1,03
1,09
1,09
1,10
1,08
1,08
0,59
0,61
0,61
1,09
1,04
1,03
0,59
0,63
0,65
δv
0,09
0,08
0,08
0,10
0,11
0,11
0,11
0,11
0,11
0,06
0,06
0,06
0,11
0,10
0,10
0,06
0,06
0,07
δtStoss→Boden
0,02
0,02
0,02
0,02
0,02
0,02
p
0,040
0,034
0,034
0,069
0,073
0,073
0,048
0,047
0,047
0,039
0,041
0,041
0,047
0,045
0,045
0,039
0,042
0,043
δp
0,006
0,005
0,005
0,010
0,011
0,011
0,007
0,007
0,007
0,006
0,006
0,006
0,007
0,007
0,007
0,006
0,006
0,006
pGesamt Stoß δpStoss
0,109
0,016
0,107
0,016
0,107
0,016
0,087
0,013
0,088
0,013
0,088
0,013
0,088
0,013
0,087
0,013
0,088
0,013
5 AUSWERTUNG
Zur Berchnung der Energie wird diese Formel verwendet:
1
Ekin = mv 2
2
Für die Fehlerrechnung werden folgende Formeln verwendet:
Zunächst wird nur der Fehler der kinetischen Energie bestimmt.
δEkin
1
δm
= ∗(
+2∗
Ekin
2
m
δm
Ekin
∗(
+2∗
⇒ δEkin =
2
m
Versuchsreihe
*
#
@
Wurf
Einzeln G
Einzeln K
G gem 1
K gem 1
G gem 2
K gem 2
G gem 3
K gem 3
Einzeln G
Einzeln K
G gem 1
K gem 1
G gem 2
K gem 2
G gem 3
K gem 3
Einzeln G
Einzeln K
G gem 1
K gem 1
G gem 2
K gem 2
G gem 3
K gem 3
v
0,95
0,99
1,03
0,919
1,09
0,777
1,09
0,791
0,64
1,00
0,59
1,10
0,61
1,08
0,61
1,08
0,65
1,01
0,59
1,09
0,63
1,04
0,65
1,03
δv
0,04
0,04
0,10
0,09
0,11
0,08
0,11
0,08
0,03
0,04
0,06
0,11
0,06
0,11
0,06
0,11
0,03
0,04
0,06
0,11
0,06
0,10
0,07
0,10
17
δv
)
v
δv
)
v
Ekin δEkin
0,030 0,001
0,021 0,001
0,035 0,003
0,018 0,001
0,040 0,003
0,013 0,001
0,040 0,003
0,014 0,001
0,014 0,001
0,022 0,001
0,012 0,001
0,026 0,002
0,012 0,001
0,025 0,002
0,012 0,001
0,025 0,002
0,014 0,001
0,022 0,001
0,012 0,001
0,026 0,002
0,013 0,001
0,023 0,002
0,014 0,001
0,023 0,002
(38)
(39)
Ekin,Gesamt
δEkin,Gesamt
0,051
0,002
0,053
0,004
0,053
0,004
0,054
0,004
0,036
0,002
0,036
0,003
0,037
0,003
0,037
0,003
0,036
0,002
0,038
0,003
0,036
0,003
0,037
0,003
1 FRAGE 1: ROTATION VON ROLLENDEN KUGELN
6. Fehlerbetrachtung
Im Allgemeinen gilt, dass die Abweichung innerhalb unsereres Fehlers liegt. Somit kann
man sagen, dass bei diesem Versuch die Impulserhaltung und die Energieerhaltung im
Rahmen unseres Fehlers gilt.
Zu Fehlern in unseren Werten führen vor allem unsere Messungenauigkeiten. Außerdem
entstehen noch Fehler durch die Verwendung von idealisierten Systemen, so nehmen wir
z.B. keine Reibung beim Fall der Kugel an. Auch nehmen wir an, dass beim Stoß keine
Energie verloren geht, die Kugeln also einen elastischen Stoß durchführen. Auch dies
ist in der Praxis nicht ganz korrekt. Diese Annahmen können wir aber nicht in unsere
Berechnung einfließen lassen, wodurch wir dieses nur Abschätzen können.
Teil IV.
Fragen
1. Frage 1: Rotation von rollenden Kugeln
Warum würde man nicht die richtige Fluggeschwindigkeit der Kugeln vor dem Stoß erhalten, wenn man versuchen würde, nach dem Energieerhaltungssatz die Lageenergie der
Kugeln an den Elektromagneten in kinetische Energie der Translationsbewegung am Ende der Bahn umzurechnen? Wie müsste man stattdessen rechnen?
Antwort:
Die Lageenergie ist die potentielle Energie, die die Kugel ganz zu Beginn hat. Die kinetische Energie der Translationsbewegung ist die Bewegungsenergie. Die potentielle
Energie, die die Kugel am Elektromagneten hat, wird bis zum Ende der Bahn, wenn
dies als Nullpotiential gesetzt wird, komplett in andere Energiearten umgewandelt. Das
meiste wird in Bewegungsenergie umgewandelt, aber da eine Kugel, wenn sie rollt, aber
auch rotiert, ist nicht die komplette potentielle Energie Epot0 in Bewegungsenergie T1
umgewandelt, sondern ein Teil der Energie wird in Rotationsenergie Erot1 umgewandelt.
Epot0 = T1 + Erot1
(40)
Aus Gleichungen (12) und (9) sowie (7) folgt:
1
1
mgh0 = mv12 + Jω12
2
2
18
(41)
1 FRAGE 1: ROTATION VON ROLLENDEN KUGELN
Für eine Kugel mit der Masse m,dem Trägheitsmoment nach Gleichung (4) und der
Winkelgeschwindigkeit nach Gleichung (8):
1 2 1 2 2 v1 2
mgh0 = mv1 + · mr
2
2 5
r
r
10 · gh0
⇔ v1 =
7
19
(42)
(43)
2 QUELLEN
Teil V.
Anhang
1. Abbildungs- und Tabellenverzeichnis
Abbildungsverzeichnis
1.
2.
3.
Gewöhnliche Zykloide . . . . . . . . . . .
zwei Kugeln rollen von unterschiedlichen
Zeitintervall an das Ende der Bahn . . .
Aufbau . . . . . . . . . . . . . . . . . . .
. . . . . . . . .
Startpositionen
. . . . . . . . .
. . . . . . . . .
. . . . . . . . .
in dem selben
. . . . . . . . .
. . . . . . . . .
4
5
10
2. Quellen
• Skriptum - Vorlesung zum Integrierten Kurs, Prof. Dr. Wokfgang Belzig & Prof.
Dr. Thomas Dekorsy, November 2006
• Demtröder, Wolfgang: Experimentalphysik 1, 5. Auflage, Springer Verlag, 2008
• Vorlesungsmitschrift vom WS 2011/12, Prof. Dr. Ulrich Nowak & Prof. Dr. Thomas
Dekorsy
• Fehlerrechnung des Anfänger Praktikums
20