Technische Informatik I

Technische Informatik I
Prof. Dr. M. Radetzki
Universität Stuttgart
Vorlesung im Sommersemester 2009
Folienmaterial mit freundlicher Genehmigung von
Dr. D. Stoffel, TU Kaiserslautern
Folie 1-1
Einführung
Vorlesungstermine
Termine:
• montags,
• dienstags,
11.30 – 13.00 Uhr, V38.01
11.30 – 13.00 Uhr, V38.01
Achtung!
Nicht an jedem Termin findet eine Vorlesung statt!
Die jeweils nächsten Termine werden in der Vorlesung
bekanntgegeben.
Terminvorschau außerdem auf der Vorlesungs-Webseite:
http://www.iti.uni-stuttgart.de
→ Kurse
→ Sommersemester 2009
→ Vorlesung Technische Informatik I
Folie 1-2
Einführung
Übungen - Ablauf
•
•
•
•
Gruppenübungen (Tutorien)
5 Übungsgruppen
Insgesamt 5 Übungstermine pro Gruppe
Übungsblätter können von der Übungswebseite
heruntergeladen werden
• Übungen werden von der Abteilung Parallele Systeme (Prof.
Simon) durchgeführt
http://www.ipvs.uni-stuttgart.de
→ Abteilungen: Parallele Systeme
→ Lehre: Lehrveranstaltungen
→ Technische Informatik 1 Übung
→ Materialien
Folie 1-3
Einführung
Online-Anmeldung zu den Übungen
Zu den Übungen ist eine Online-Anmeldung erforderlich. Die
Anmeldungs-Webseite ist über die Übungs-Webseite erreichbar:
http://uebungsgruppen.informatik.uni-stuttgart.de
→Technische Informatik
→ Übungen zu Technische Informatik I
Dienstags,
15:45-17:15 Uhr in 0.363, 14-tägig
Dienstags,
17:30-19:00 Uhr in 0.108, 14-tägig
Donnerstags, 14:00-15:30 Uhr in 0.463, 14-tägig
Die Online-Anmeldung wird ab
Dienstag, 21.04.2009, 14:00 Uhr
freigeschaltet.
Anmeldung möglich bis Freitag, 24.04.2009, 18:00 Uhr!
Folie 1-4
Einführung
Sonstiges
Kriterien für Erwerb des Übungsscheins:
• Anwesenheitspflicht und aktive Mitarbeit in der Übung als
Voraussetzung für die Zulassung zur Scheinklausur
• Scheinklausur in der letzten Vorlesungswoche
(lernen Sie vorlesungsbegleitend!)
• Auch wenn Sie den Schein nicht brauchen: die Inhalte dieser
Vorlesung machen 50% der Prüfungsklausur aus!
Skript/Folien:
• Tafelanschrieb mitschreiben!
• Buch „Technische Informatik 1“ in der Inf.-Bibliothek.
• Folien stehen über die Vorlesungs-Webseite zur Verfügung.
• Benutzername und Passwort am Ende dieser Vorlesung.
Folie 1-5
Technische Informatik I
Technische Informatik I
Prof. Dr. Martin Radetzki
Universität Stuttgart
Kapitel 1
Einführung
Folie 1-1
Einführung
Informationstechnik – Technische Informatik
Informationstechnische Systeme
halten Einzug in viele Bereiche
des täglichen Lebens:
PC, Handy, Multimedia,
Automobil etc.
Überall im Alltag stoßen wir auf technische Systeme, die Information speichern,
übertragen und verarbeiten.
Folie 1-2
Einführung
Technische Informatik
Die Technische Informatik ist ein wichtiges Grundgebiet der
Informatik.
Ihr Gegenstand sind die Techniken, die die
Speicherung,
Übertragung und
Verarbeitung
von Information ermöglichen.
Was ist Information ? „etwas Wissbares“ (S. Wendt)
Was ist „wissbar“ ? …
(unsere intuitive Vorstellung soll uns genügen)
Information wird in physikalisch realisierbaren Mustern symbolisiert: „Daten“
(In der Informatik betrachten wir meistens nur die Daten, nicht die symbolisierte
Information.)
Folie 1-3
Einführung
Speicherung
von Information (oder „Daten“) in technischen Systemen
Speichermedien sind beispielsweise:
Hauptspeicher eines Computers (RAM), Festplatte eines Computers, FlashSpeicher, CDs, DVDs, Plastikkarte mit Magnetstreifen, Leitz-Ordner
Wie realisiere ich elektronische Speichermedien physikalisch?
Mit dieser Frage beschäftigen sich beispielsweise Mikroelektronik oder
Halbleiterphysik.
Folie 1-4
Einführung
Speicherung
von Information (oder „Daten“) durch technische Systeme
Es kommen wichtige Fragen hinzu:
Wie strukturiert, wie repräsentiert man die Information, so dass man:
• sie möglichst einfach (und schnell) abspeichern kann?
• sie möglichst einfach (und schnell) wieder abrufen kann?
• möglichst wenig Ressourcen benötigt?
Solche Fragen werden z.B. in der Datenbanktechnik behandelt, wo es darum geht,
große Mengen von Daten zu verwalten,
oder z.B. in der Rechnerarchitektur, wo man sich Speicherhierarchien
(Register→Cache→Hauptspeicher→Festplatte →Magnetband) überlegt, um eine
möglichst schnelle und dennoch kostengünstige Informationsverarbeitung zu
gewährleisten.
Folie 1-5
Einführung
Übertragung
von Information (oder „Daten“) durch technische Systeme
Information (Daten) wird heute in Kommunikationsnetzwerken übertragen, in
denen unterschiedliche Übertragungsstrecken zusammengeschaltet sind. Damit
beschäftigt sich die Kommunikationstechnik.
Beispiele für Übertragungsstecken:
Richtfunk, Kupferkabel, Glasfaserkabel,
per Satellit etc.
Wie realisiert man Kommunikationsnetzwerke mit guten physikalischen
Übertragungseigenschaften?
Aber auch:
Wie repräsentiert („kodiert“) man Information, so dass man in möglichst kurzer
Zeit unter Aufwendung möglichst geringer Ressourcen möglichst viel
Information übertragen und möglichst einfach weiterverarbeiten kann?
Folie 1-6
Einführung
Verarbeitung
von Information (oder „Daten“) durch technische Systeme
Information (Daten) wird in technischen Systemen unterschiedlicher Art
verarbeitet.
Der Informationsverarbeitung in technischen Systemen liegt stets ein formales
Verfahren zugrunde, also eine Abfolge von vorher festgelegten elementaren
Verfahrensschritten.
Im Unterschied dazu verarbeitet der Mensch Information häufig ohne ein (ihm
bewusstes) formales Verfahren.
Folie 1-7
Einführung
Beispiele
informationsverarbeitender Systeme
Der Getränkeautomat
Eingabe von Daten in Form von
unterschiedlichen Münzen und mit einer
Tastatur zur Auswahl einer Getränkesorte
Ausgabe einer Getränkedose und von
Wechselgeld entsprechend der eingeworfenen
Geldsumme
Der Getränkeautomat muss ein einfaches formales Verfahren besitzen, mit
dem er für jede Eingabe entscheidet, ob eine Getränkedose bestimmten Typs
ausgegeben wird und wieviel Wechselgeld zurückgegeben wird.
Folie 1-8
Einführung
Beispiele
informationsverarbeitender Systeme
Das Überdruckventil eines Schnellkochtopfs
Eingabe ist der Dampfdruck im Inneren des Topfes.
Ausgabe ist ein Pfeifgeräusch, das ertönt, wenn der Druck einen bestimmten
Schwellenwert übersteigt, sowie das Auslösen des Ventils, um den Dampf
entweichen zu lassen.
Das Überdruckventil kann z. B. durch eine einfaches mechanisches Verfahren
basierend auf einer Feder realisiert werden.
Folie 1-9
Einführung
Beispiele
informationsverarbeitender Systeme
Der Computer
Eingabe von Daten über Tastatur, Maus, Netzwerk und andere periphere Geräte
Ausgabe von Daten über Monitor, Lautsprecher, Netzwerk, Drucker und andere
periphere Geräte
Durch Programmierbarkeit können je nach Anwendung und Art der Ein-/Ausgabedaten unterschiedliche formale Verfahren zur Informationsverarbeitung
„implementiert“ werden:
z.B.
•
•
•
•
Verfahren zur Lösung mathematischer Probleme
Verfahren zur Steuerung von produktionstechnischen Anlagen
Verfahren zur Unterstützung verwaltungstechnischer und betrieblicher Abläufe
Verfahren zur Unterstützung von Entwurfsprozessen (CAD)
Folie 1-10
Einführung
Verarbeitung
von Information (oder „Daten“) durch technische Systeme
Wie realisiert man informationsverarbeitende Systeme?
Wie realisiert man die physikalischen Vorgänge, die informationsverarbeitenden
Prozessen zugrunde liegen?
Dies ist eine Fragestellung der Mikroelektronik, der Elektronik und der
Schaltungstechnik.
Wie strukturiert man die Information und ihre Verarbeitung?
Welche informationellen Strukturen und welche Formalismen legt man
informationsverarbeitenden Systeme zugrunde?
Dies ist eine Fragestellung der Informatik.
Folie 1-11
Einführung
Verarbeitung
von Information (oder „Daten“) durch technische Systeme
Beispiel: Formalismus zur Darstellung nichtnegativer ganzer Dezimalzahlen als
Dualzahl
Man gibt zur Identifikation einer Zahl jeweils diejenigen Zweierpotenzen an, deren
Summe die gemeinte Zahl ist. Zum Beispiel ist mit 11001 die Zahl fünfundzwanzig
gemeint, weil 1·24 + 1·23 + 0·22 + 0·21 + 1·20 = 16 + 8 + 1 = 25 ist.
Für ein physikalisches System zur Darstellung einer Dualzahl gibt es viele
Möglichkeiten, z.B. eine Folge von Speicherzellen (Bits) in einem Register, eine
Folge von Leuchtdioden, eine Lochkarte, etc.
Zum Verständnis der Funktion eines solchen Systems benötigt man beides:
•
Kenntnis der elektrotechnisch/physikalischen Realisierung,
•
Kenntnis des zugrundeliegenden Formalismus, mit dem eineInterpretation
verbunden ist. Diese muss man kennen, wenn man das System seinem Zweck
entsprechend einsetzen will.
Folie 1-12
Einführung
Die Trennung zwischen den informationellen Strukturen eines informationstechnischen Systems, die man mit bestimmten Formalismen beschreiben kann und
den Techniken zu ihrer physikalischen Realisierung ist unvermeidlich, wenn man
große, komplexe Systeme entwerfen will.
Beispiel: Computerprogramm
Ein Programm ist zunächst lediglich eine Beschreibung eines technischen Systems. Es
ist selbst nicht zu Wechselwirkungen mit seiner Umwelt fähig. Im Bereich software
engineering beschäftigt man sich mit den Strukturen eines Programms. Sie sind nicht
mit den Strukturen des durch das Programm beschriebenen Systems zu verwechseln.
Das beschriebene System wird realisiert, indem man das Programm in ein programmierbares System einbringt, so dass es sich gemäß dem Programm verhalten kann.
Während man das Programm entwirft, braucht man sich nicht mit den technischen
Realisierungen zu beschäftigen, für die es viele Möglichkeiten gibt. Während man die
technischen Realisierungen entwirft, braucht man sich nicht mit den Programmen
beschäftigen, die später darauf abgearbeitet werden sollen.
Nur durch diese Trennung ist es möglich, große Systeme zu entwerfen.
Folie 1-13
Einführung
Thema der Vorlesung "Technische Informatik I"
physikalische/elektrotechnische
Hilfsmittel,
einfache Bausteine zur Realisierung
informationstechnischer Systeme
mathematische Hilfsmittel
(Formalismen)
zur Beschreibung
informationstechnischer Systeme
Methodik für den Entwurf komplexer
informationstechnischer Systeme
In dieser Vorlesung betrachten wir die elektrotechnischen Grundlagen
der technischen Informatik und die Anwendung ihrer Formalismen auf
den Entwurf digitaler Schaltungen.
Folie 1-14
Einführung
Beispiel: Signale
Information kann in unterschiedlichen physikalischen Erscheinungsformen
übermittelt werden, z.B. mittels
Schallwellen, Spannungs- und Stromschwankungen in einem Leiter, elektromagnetischen Wellen.
Die Prozesse der räumlichen und zeitlichen Änderung dieser physikalischen
Größen beschreiben wir mathematisch durch Signale.
Auf Signale und ihre Klassifikation wird später noch genauer eingegangen.
Die meisten technischen Systeme zur Informationsverarbeitung verbinden
Information mit bestimmten Objekten, z.B. Münzen (Getränkeautomat) oder
binäre Zahlen (Computer). Kennzeichen dieser Objekte ist, dass sie voneinander
unterscheidbar (diskret) und somit abzählbar sind.
Folie 1-15
Einführung
Digital versus analog
Digitale und analoge Signale
+5
+5
1
0
1
V
V
Zeit
Zeit
–5
Digital:
es können nur diskrete Werte
angenommen werden (hier werden
sogar nur zwei Werte unterschieden,
es handelt sich deshalb um ein
binäres Signal)
–5
Analog:
Werte variieren kontinuierlich über
den gesamten Wertebereich
Folie 1-16
Einführung
Vorteile digitaler Systeme
Analoges System: kleine Schwankungen am Eingang können zu großen
Schwankungen am Ausgang führen
Digitales System: höhere Robustheit und Genauigkeit, kleine Signalschwankungen
werden „wegabstrahiert“
einzelne Systemkomponenten können leichter zusammengesetzt
werden
Computer benutzen intern digitale Schaltungen.
Die reale physikalische Welt ist analog. Interface-Schaltungen (z.B. Sensoren und
Aktuatoren) sind daher meist analog.
Folie 1-17
Einführung
Digitale Hardware
Binäre Systeme
• Zwei diskrete Werte:
on, 5 Volt, high, Strom fließt, magnetischer Nordpol, "1"
off, 0 Volt, low, kein Strom fließt, magnetischer Südpol, "0"
• Vorteile binärer Systeme:
sehr gut durch Gesetze der mathematischen Logik beschreibbar,
vor allem: technologisch leicht realisierbar
Beispiel:
WENN
WENNdie
dieAmpel
Ampelfür
fürdie
dieHauptstraße
Hauptstraßegrün
grünist
ist
UND
die
Ampel
für
die
einmündende
Straße
UND die Ampel für die einmündende Straßerot
rotist
ist
UND
UND45
45Sekunden
Sekundenseit
seitdem
demletzten
letztenWechsel
Wechselvergangen
vergangensind,
sind,
DANN
wird
die
Ampel
für
die
Hauptstraße
gelb
DANN wird die Ampel für die Hauptstraße gelb
Folie 1-18
Einführung
Beispiel einer Implementierung
Beispiel einer Implementierung eines informationstechnischen
Systems mit Hilfe eines Netzwerkes von Schaltern:
Jeder Schalter wird von einem Steuersignal bedient.
Man kann mit einem solchen Schalternetzwerk die Gültigkeit
logischer Aussagen bestimmen.
Hauptstraße
grün
True
einmündende
Straße rot
45 s seit
letztem Wechsel
Hauptstraße
wird gelb
WENN
WENNdie
dieAmpel
Ampelfür
fürdie
dieHauptstraße
Hauptstraßegrün
grünist
ist
UND
die
Ampel
für
die
einmündende
Straße
UND die Ampel für die einmündende Straßerot
rotist
ist
UND
UND45
45Sekunden
Sekundenseit
seitdem
demletzten
letztenWechsel
Wechselvergangen
vergangensind,
sind,
DANN
wird
die
Ampel
für
die
Hauptstraße
gelb
DANN wird die Ampel für die Hauptstraße gelb
Folie 1-19
Einführung
Gliederung
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
Einführung
Physikalische und mathematische Grundbegriffe
Das elektrostatische Feld
Elektrischer Strom und elektrische Netzwerke
Elektromagnetische Vorgänge
Halbleiterbauelemente
Digitale Grundschaltungen
Optimierung von Schaltnetzen
Bausteine digitaler Entwürfe
Automaten als Verhaltensmodelle sequenzieller Netzwerke
Schaltwerke
Funktionseinheiten sequenzieller Systeme
Aufbau eines Rechners
Entwurfsautomatisierung
Folie 1-20
Einführung
Literatur (1)
Manfred Albach:
Grundlagen der Elektrotechnik I
2004, Pearson Studium Verlag, ISBN 3-8273-7106-6, 292 S.
Wolfram Schiffmann, Robert Schmitz:
Technische Informatik 1
5. Aufl., 2004, Springer-Verlag, ISBN 3-540-40418-7, 337 S.
Bernd Becker, Rolf Drechsler, Paul Molitor:
Technische Informatik
Eine Einführung.
2005, Pearson Studium Verlag, ISBN 3-8273-7092-2, 390 S.
Randy Katz:
Contemporary Logic Design
1994, Benjamin/Cummings-Verlag, ISBN 0-8053-2703-7.
Folie 1-21
Einführung
Literatur (2)
U. Schöning:
Logik für Informatiker
1995, Spektrum Lehrbuch, Akademischer Verlag, ISBN 3-86025-684-X.
S. Wendt:
Nichtphysikalische Grundlagen der Informationstechnik
Interpretierte Formalismen
1991, Springer-Verlag, ISBN 3-540-54452-6, 487 S.
Folie 1-22
Technische Informatik I
Prof. Dr. Martin Radetzki
Universität Stuttgart
Kapitel 2
Physikalische und mathematische Grundbegriffe
Folie 2-1
Physikalische und mathematische Grundbegriffe
Physikalische Größen
Die Physik befasst sich mit messbaren Eigenschaften von Naturvorgängen
und den zwischen ihnen bestehenden gesetzmäßigen Beziehungen.
Eigenschaften werden durch den Begriff „Physikalische Größe“
bezeichnet.
Physikalische Größen sind beispielsweise:
•
•
•
•
•
Länge (gemessen in Meter,m)
Zeit (gemessen in Sekunde,s)
Kraft (gemessen in Newton,N)
elektrische Spannung (gemessen in Volt,V)
...
Physikalische Größen sind durch mathematische Gleichungen, so
genannte Größengleichungen, miteinander verknüpft. Diese Gleichungen
beschreiben physikalische Gesetzmäßigkeiten, beispielsweise:
Spannung = elektrischer Widerstand mal Stromstärke
U=R•I
(Ohm'sches Gesetz)
Folie 2-2
Physikalische und mathematische Grundbegriffe
Physikalische Größen
Der Wert einer physikalischen Größe ist das Produkt aus einem
Zahlenwert und einer Einheit:
Wert der Größe = Zahlenwert • Einheit
Bsp.: U = 5,2 V bedeutet:
gemessene Spannung U beträgt das 5,2fache eines Volt.
Zahlenwert = 5,2
Einheit = V
Zur besonderen Kennzeichnung der Einheit wird die eckige Klammer
verwendet.
Bsp.: [I] = A bedeutet:
die Einheit der elektrischen Stromstärke I ist Ampere.
Folie 2-3
Physikalische und mathematische Grundbegriffe
Basisgrößenarten
In der Physik werden 7 Basisgrößenarten verwendet. Sie sind voneinander
unabhängig. Von ihnen lassen sich alle anderen Größen ableiten. Die
Basiseinheiten sind im internationalen Système International d’Unités (SI)
festgelegt.
übliches
Formelzeichen
SI-Basiseinheit
Länge
l
das Meter (m)
Masse
m
das Kilogramm (kg)
Zeit
t
die Sekunde (s)
elektrische Stromstärke
I
das Ampere (A)
Temperatur
T, ϑ
das Kelvin (K)
Stoffmenge
n
das Mol (mol)
Lichtstärke
IV
die Candela (cd)
MKSA-System
Basisgrößenart
Für die Beschreibung mechanischer sowie elektromagnetischer Vorgänge
reichen die vier SI-Basisgrößen des MKSA-Systems (Meter, Kilogramm,
Sekunde, Ampere) aus.
Folie 2-4
Physikalische und mathematische Grundbegriffe
Abgeleitete Einheiten
Aus den Basiseinheiten lassen sich durch Multiplikation, Division und
Potenzierung abgeleitete Einheiten bilden, die ihrerseits einen eigenen
Namen bzw. ein eigenes Zeichen besitzen können.
Beispiele:
[Ladung] = Coulomb
[Q] = C
mit 1 C = 1 As
[Kraft] = Newton
[F] = N
mit 1 N = 1 kg m/s2
[Frequenz] = Hertz
[f] = Hz
mit 1 Hz = 1/s
Die Dimension dim x einer Größe x gibt den Zusammenhang
zwischen x und den Basisgrößen an. Sie wird als Produkt von
Potenzen der Basisgrößen-Formelzeichen angegeben.
Beispiel: Die Dimension der Geschwindigkeit v (= Weg/Zeit) lautet
dim v = l t–1
Folie 2-5
Physikalische und mathematische Grundbegriffe
Weitere Einheiten
Neben den SI-Einheiten existieren noch einige andere Einheiten für die
Anwendung in speziellen Gebieten. Ihr Zusammenhang mit den SIEinheiten wird experimentell ermittelt. Die für uns wichtigen Beispiele sind
das Elektronenvolt (eV) und die atomare Masseneinheit (u).
Ein Elektronenvolt (eV) entspricht der kinetischen Energie, die ein
Elektron beim Durchlaufen einer Potenzialdifferenz von 1 V im Vakuum
gewinnt.
1eV = 1,6021892 · 10–19 J
Die atomare Masseeinheit u wird angegeben in kg und entspricht 1/12 der
Masse eines Kohlenstoffisotops 12C.
1u = 1,66057 · 10–27 kg
Folie 2-6
Physikalische und mathematische Grundbegriffe
SI-Vorsätze
Ist der Zahlenwert einer physikalischen Größe unpraktisch groß
oder klein, so kann eine Zehnerpotenz der Einheit verwendet
werden.
Die Zehnerpotenz wird durch einen der folgenden Vorsätze
gekennzeichnet:
Potenz Name Zeichen
Potenz Name Zeichen
1015
Peta
P
10-3
Milli
m
1012
Tera
T
10-6
Mikro
µ
109
Giga
G
10-9
Nano
n
106
Mega
M
10-12
Piko
p
103
Kilo
k
10-15
Femto
f
Folie 2-7
Physikalische und mathematische Grundbegriffe
SI-Vorsätze
Der Vorsatz wird so gewählt, dass der Zahlenwert der Größe
zwischen 0,1 und 1000 liegt.
Bsp.: Ein Radiosender sendet auf einer Frequenz von 106 300 000 Hertz
106 300 000 Hz = 106 300 kHz = 106,3 MHz
Anmerkung:
Eine Besonderheit bildet die SI-Basiseinheit Kilogramm (kg). Die Vorsätze
werden nicht auf kg, sondern auf die Einheit Gramm (g) angewendet.
Beispielsweise werden 10-3 g als mg und nicht als µkg bezeichnet.
Folie 2-8
Physikalische und mathematische Grundbegriffe
Skalare und vektorielle Größen
Physikalische Größen sind entweder Skalare oder Vektoren.
Skalare Größen sind durch Zahlenwert und Einheit vollständig
charakterisiert.
Beispiele skalarer Größen:
Zeit t, Temperatur T, elektrische Ladung Q, Masse m, ...
Vektorielle Größen haben neben Zahlenwert und Einheit auch noch
eine Richtung.
Beispiele vektorieller Größen:
Geschwindigkeit v, Kraft F, elektrische Feldstärke E, ...
Benötigt man von einer vektoriellen Größe A nur Zahlenwert und
Einheit, also den Betrag des Vektors A, so schreibt man |A| oder nur
kurz A.
Folie 2-9
Physikalische und mathematische Grundbegriffe
Freie und gebundene Vektoren
In der Physik unterscheidet man zwischen freien Vektoren und
gebundenen Vektoren.
Bei freien Vektoren spielt die Position ihres Anfangspunktes keine
Rolle, d.h. sie können frei im Raum verschoben werden.
Gebundene Vektoren sind an ihren Anfangspunkt gebunden und
somit ortsabhängig.
Bsp.:
die Feldvektoren der elektrischen Feldstärke. Sie sind im
Allgemeinen von Ort zu Ort nach Betrag und Richtung verschieden.
Vektoren, die in einem festen Punkt (z.B. dem Koordinatenursprung)
beginnen, können überhaupt nicht verschoben werden und heißen
Ortsvektoren.
Axiale Vektoren tragen die Information eines Drehsinns. Ihre
Richtung verläuft parallel (oder antiparallel) zur Drehachse. Das
Vorzeichen kennzeichnet den Drehsinn.
Folie 2-10
Physikalische und mathematische Grundbegriffe
Negativer Vektor, Einheitsvektor, Nullvektor
Unter einem Vektor -a versteht
man einen Vektor mit dem
gleichen Betrag wie +a, aber
mit entgegengesetzter Richtung.
Ein Vektor vom Betrag 1 wird
Einheitsvektor genannt. Jeder
Vektor kann aus einem Betrag
(seiner Länge) und einem in
Richtung des Vektors
zeigenden Einheitsvektor
dargestellt werden.
Der Nullvektor 0 ist ein Vektor mit Betrag 0. Er hat keine Richtung.
Für den Nullvektor ist auch die Schreibweise 0 (ohne Vektorpfeil)
gebräuchlich.
Folie 2-11
Physikalische und mathematische Grundbegriffe
Addition und Subtraktion von Vektoren
Vektoraddition a+b:
Parallelverschiebung und
"Aneinanderhängen".
Die Vektoraddition ist
kommutativ:
Vektorsubtraktion –b:
Bildung von –b, danach
Vektoraddition:
r
r r r
a − b = a + ( −b )
r r r r
a+b =b +a
Folie 2-12
Physikalische und mathematische Grundbegriffe
Multiplikation von Vektor und Skalar
Die Multiplikation eines Vektors mit einem Skalar ergibt wieder
einen Vektor gleicher (oder entgegegengesetzter) Richtung.
a
b = ·a ,
b = ·a ,
>0
<0
Folie 2-13
Physikalische und mathematische Grundbegriffe
Skalarprodukt ("inneres Produkt")
Das Skalarprodukt a·b zweier Vektoren a und b ist ein Skalar und
ist definiert als:
a·b = |a|·ea · |b|·eb = a·b·cos
Folie 2-14
Physikalische und mathematische Grundbegriffe
(Skalarprodukt)
Das Skalarprodukt ist kommutativ:
a·b = b·a
Das Skalarprodukt ist distributiv bezüglich der
Vektoraddition und Vektorsubtraktion:
a·(b + c) = a·b + a·c
Für parallele bzw. senkrecht aufeinander stehende Vektoren a und b
gelten folgende Spezialfälle:
a·b = ab
wenn a und b parallel sind
a·b = 0
wenn a und b senkrecht zueinander sind
a·b = –ab
wenn a und b antiparallel sind
Folie 2-15
Physikalische und mathematische Grundbegriffe
Vektorprodukt ("Kreuzprodukt", "äußeres Produkt")
Das Vektorprodukt a×b zweier Vektoren a und b ist ein Vektor c
definiert durch:
Betrag:
|c| = |a|·|b|·sin
= ab sin
Richtung: c steht senkrecht auf der von a und b
aufgespannten Ebene und zwar so, dass
a, b und c ein Rechtssystem bilden.
Folie 2-16
Physikalische und mathematische Grundbegriffe
(Vektorprodukt)
Das Vektorprodukt ist nicht kommutativ:
a×b = – b×a
Das Vektorprodukt ist distributiv bezüglich der
Vektoraddition und Vektorsubtraktion:
a×(b + c) = a×b + a×c
Für parallele bzw. senkrecht aufeinander stehende Vektoren a und b
gelten folgende Spezialfälle:
a×b = 0
wenn a und b parallel sind
a×b = ab ec
wenn a und b senkrecht zueinander stehen
a×b = 0
wenn a und b antiparallel sind
Folie 2-17
Physikalische und mathematische Grundbegriffe
Kartesisches Koordinatensystem
Die Koordinatenachsen sind
zueinander orthogonal.
Die Einheitsvektoren ex, ey und ez
verlaufen parallel zu den Koordinatenachsen und bilden ein Rechtssystem.
Ein Raumpunkt P wird bezogen auf
den Koordinatenursprung 0 durch einen
Ortsvektor r der Länge r = | r |
beschrieben.
r = x ex + y ey + z ez
r
r = r = x2 + y2 + z2
Folie 2-18
Physikalische und mathematische Grundbegriffe
Vektoroperationen im kartesischen Koordinatensystem
Mit a = ax ex + ay ey + az ez und b = bx ex + by ey + bz ez lassen sich die
Vektoroperationen in kartesischen Koordinaten wie folgt berechnen:
Vektoraddition: a + b = (ax + bx) ex + (ay + by) ey + (az + bz) ez
Vektorsubtraktion: a – b = (ax – bx) ex + (ay – by) ey + (az – bz) ez
Multiplikation mit Skalar:
Skalarprodukt:
a =
a x ex + a y ey + a z ez
a · b = axbx + ayby + azbz
Vektorprodukt: a × b = (aybz – azby) ex + (azbx – axbz) ey + (axby – aybx) ez
Folie 2-19
Physikalische und mathematische Grundbegriffe
Beispiele krummliniger Koordinatensysteme
Zylinderkoordinaten
Ein Raumpunkt P wird durch die Koordinaten , und z beschrieben.
Die (ortsabhängigen) Einheitsvektoren e , e und ez bilden in jedem
Raumpunkt ein orthogonales Rechtssystem.
Folie 2-20
Physikalische und mathematische Grundbegriffe
Beispiele krummliniger Koordinatensysteme
Kugelkoordinaten
Ein Raumpunkt P wird durch die Koordinaten r, ϑ und beschrieben.
Die (ortsabhängigen) Einheitsvektoren er, eϑ und e bilden in jedem
Raumpunkt ein orthogonales Rechtssystem.
Folie 2-21
Technische Informatik I
Prof. Dr. Martin Radetzki
Universität Stuttgart
Kapitel 3
Das elektrostatische Feld
Folie 3-1
Elektrostatisches Feld
Bohr'sches Atommodell
Niels Bohr (1885-1962)
–
–
0 + 0 Atomkern, ∅ ~ 10-14 m
+0+
0+
–
+
Proton
–
Elektron
0
Neutron
Elektronenhülle, ∅ ~ 10-10 m (!)
–
Folie 3-2
Elektrostatisches Feld
Elektrische Ladung
Die kleinste (nicht weiter teilbare) Ladungsmenge heißt
Elementarladung e = 1.6021892·10-19 As
Protonen tragen die Ladung +e.
Elektronen tragen die Ladung –e.
Da die Anzahl der Protonen und Elektronen in den Atomen gleich groß ist,
verhalten sich Atome nach außen elektrisch neutral.
Ladungen sind stets ein Vielfaches der Elementarladung.
In einem abgeschlossenen System ist die Summe der Ladungen stets
konstant.
Ladungen gleichen Vorzeichens stoßen sich gegenseitig ab.
Ladungen unterschiedlichen Vorzeichens ziehen sich gegenseitig an.
Folie 3-3
Elektrostatisches Feld
Coulomb'sches Gesetz
Durch Messung hat Charles Augustin de
Coulomb (1736-1806) für die Kraft F zwischen
zwei Punktladungen Q1 und Q2 festgestellt:
Q1Q2
F~ 2
r
Die Proportionalitätskonstante ist 1/4 0. Der Faktor 0 heißt
elektrische Feldkonstante und beträgt 0 = 8,854·10-12 As/Vm.
Mit der Festlegung eines
Einheitsvektors er in Richtung
von Q1 nach Q2 ergibt sich der
Kraftvektor nach Betrag und
Richtung zu:
r
F=
1 Q1Q2 r
er
2
4πε 0 r
Folie 3-4
Elektrostatisches Feld
Elektrisches Feld
Die Ladung Q2 erfährt durch das Vorhandensein der Ladung Q1 eine
Kraftwirkung. Die Kraftwirkung ist direkt proportional zu Q2 und abhängig
vom Ort der Ladung Q2.
Man sagt, die ruhende Ladung Q1 ruft ein elektrisches Feld hervor, das sich
durch Kraftwirkung auf Probeladungen Q2 bemerkbar macht.
r
F=
r
1 Q1 r
e ⋅ Q2 = E ⋅ Q2
2 r
4πε 0 r
r
E=
1 Q1 r
e
2 r
4πε 0 r
Die Größe E wird elektrische Feldstärke genannt und hat die Einheit V/m.
Der Zusammenhang zwischen der Kraft F auf eine Ladung Q in einem
elektrischen Feld und der elektrischen Feldstärke E lautet
r r
F = E ⋅Q
Folie 3-5
Elektrostatisches Feld
(Elektrisches Feld)
Der Begriff elektrische Feldstärke bezeichnet einen Vektor in einem speziellen
Raumpunkt. Die Gesamtheit der Feldvektoren im Raum wird als elektrisches
Feld bezeichnet.
Eine positive Punktladung ruft eine radial nach außen gerichtete elektrische
Feldstärke hervor. Bei einer negativen Punktladung zeigt der Feldstärkevektor
zur Punktladung hin.
Die Kraft auf eine positive Punktladung hat die gleiche Richtung wie die
elektrische Feldstärke an der Stelle der Punktladung. Bei einer negativen
Punktladung zeigen Feldstärke und Kraft in entgegengesetzte Richtungen.
Auf die Ladung Q2 wirkt eine Kraft infolge des durch Q1 hervorgerufenen
elektrischen Feldes. Q2 erzeugt aber ihrerseits ein elektrisches Feld, das eine
gleich große, entgegengesetzt gerichtete Kraft F1 = E2Q1 = –F2 auf die
Punktladung Q1 ausübt.
Folie 3-6
Elektrostatisches Feld
Überlagerung von Feldern
Die Gesamtfeldstärke einer aus mehreren Ladungen bestehenden Anordnung
ergibt sich durch lineare Überlagerung der Beiträge der Einzelladungen:
r
r r
1
ri
E ( rP ) =
Qi 3
∑
4πε 0 i =1, 2,... ri
mit
r r r
ri = rP − rQi
und
r
ri = ri
Bsp.: Das Feld dreier
Punktladungen Q1, Q2 und
Q3 in einem Raumpunkt P:
Folie 3-7
Elektrostatisches Feld
Darstellung von Feldern
Als Feldlinien bezeichnet man
Raumkurven, bei denen die Tangente
in jedem Punkt in Richtung der
elektrischen Feldstärke zeigt.
Die Dichte der in einem Feldlinienbild eingezeichneten Feldlinien
kann in vielen Fällen so gewählt werden, dass sie ein Maß für den
Betrag der Feldstärke darstellt.
Die Feldlinien beginnen immer bei positiven Ladungen und enden auf
negativen Ladungen.
Folie 3-8
Elektrostatisches Feld
Beispiele von Feldlinienbildern
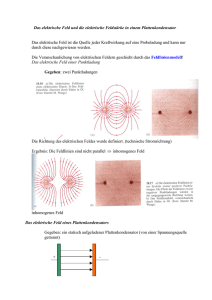
Feldlinienbilder zweier Punktladungen
Folie 3-9
Elektrostatisches Feld
(Beispiele für Feldlinienbilder)
Feldlinienbild einer einzelnen positiven Punktladung.
Zur Vereinfachung nimmt man an, dass sich die zugehörigen negativen
Ladungen auf einer unendlich fernen Hülle befinden.
Folie 3-10
Elektrostatisches Feld
(Beispiele für Feldlinienbilder)
Elektrisches Feld zwischen zwei mit den Ladungen +Q und –Q
geladenen Platten.
Folie 3-11
Elektrostatisches Feld
Arbeit
Wenn eine Kraft einen Körper auf einem bestimmten Weg verschiebt,
so verrichtet sie am Körper Arbeit.
Unter der physikalischen Größe der Arbeit W versteht man das
Produkt aus Kraft F und Weg s.
Die verrichtete Arbeit W vergrößert die Energie des Körpers um W.
SI-Einheit der Arbeit bzw. der Energie:
[W] = [F]·[s] = N·m = Joule (J) = W·s = kg·m2/s2
Wenn W die verrichtete Arbeit, F die konstante Kraft, die in
Wegrichtung wirkt und s der vom Körper zurückgelegte Weg ist,
dann gilt W = F · s.
Bilden Kraft- und Wegrichtung einen Winkel , dann darf nur die
Kraftkomponente in Wegrichtung mit dem Weg multipliziert werden:
W = F · s · cos , oder, in vektorieller Schreibweise: W = F · s.
Folie 3-12
Elektrostatisches Feld
(Arbeit)
Im allgemeinen Falle, wenn die Kraft nicht konstant, sondern nach
Betrag und Richtung ortsabhängig ist, dann ist die Arbeit das
Wegintegral der Kraft:
r r
W = ∫ F ds
P2
P1
Merke:
• Die Arbeit ist eine skalare Größe!
• Das Integral zählt die durch die Kraft verrichtete Arbeit.
• Bewegt man den Körper gegen die Kraft, so wird die aufzuwendende
Arbeit aufgrund der Eigenschaften des Skalarprodukts negativ.
Folie 3-13
Elektrostatisches Feld
Arbeit im elektrischen Feld
Auf eine Punktladung Q wirkt in einem
äußeren, durch andere Ladungen
hervorgerufenen elektrischen Feld eine
(ortsabhängige) Kraft. Verschiebt man
P
die Punktladung gegen die Feldkraft von 1
einem Punkt P1 zu einem Punkt P2, so
beträgt die aufzuwendende Arbeit:
P2
P2
r r
r r
= ∫ F ⋅ ds = Q ∫ E ⋅ ds
P2
WP1 → P2
P1
P1
Verschiebt man die Punktladung auf einem anderen Weg von P2 wieder
zurück nach P1, so ist die aufzuwendende Arbeit
P1
r r
r r
= ∫ F ⋅ ds = Q ∫ E ⋅ ds
P1
WP2 → P1
P2
P2
Folie 3-14
Elektrostatisches Feld
Konservatives Feld (Energieerhaltung)
Im elektrischen Feld wechselt das Vorzeichen der Arbeit bei Umkehrung des
Weges (Vertauschung von Start- und Endpunkt), deshalb gilt:
WP1 → P2 → P1
⎛ P2 r r ⎞ ⎛ P1 r r ⎞
⎛ P2 r r P2 r r ⎞
= ⎜ Q ∫ E ⋅ ds ⎟ + ⎜ Q ∫ E ⋅ ds ⎟ = Q ⎜ ∫ E ⋅ ds − ∫ E ⋅ ds ⎟ = 0
⎜ P
⎟ ⎜ P
⎟
⎜P
⎟
P
1
⎝ 1
⎠ ⎝ 2
⎠
⎝ 1
⎠
Darüber hinaus ist die genaue Wahl des Weges für die Arbeit unerheblich, es
kommt lediglich auf den Start- und Endpunkt an. Deshalb gilt für jeden
beliebigen geschlossenen Weg von einem beliebigen Startpunkt zu sich selbst:
r r
∫ E ⋅ ds = 0
(Ein geschlossener Integrationsweg wird durch einen
Ring im Integralzeichen gekennzeichnet.)
Diese Eigenschaft bezeichnet man als Konservativität: auf einem „Rundweg“
wird weder Energie gewonnen noch verloren; vgl. Radfahren: die beim
Bergauffahren investierte Energie wird bei der Abfahrt wieder gewonnen,
wenn man von Reibungsverlusten absieht.
Folie 3-15
Elektrostatisches Feld
Elektrostatisches Potential
Jeder Punkt des Raumes in einem
(elektrostatischen) konservativen
Feld kann durch eine skalare
Größe charakterisiert werden,
die (elektrostatisches) Potential
genannt wird, so dass gilt:
P0
ϕ2
P2
ϕ1
P1
W12 = Q ⋅ (ϕ1 − ϕ 2 )
Das Potential ist auf einen Punkt P0 bezogen (Bezugspunkt). Der Bezugspunkt
und sein Potentialwert können frei gewählt werden, da sich nur durch Addition
eines konstanten Werts auf ϕ1 und ϕ2 auswirken und so wie oben auch im
Folgenden stets nur Potentialdifferenzen verwendet werden.
Übliche Vereinbarungen für den Bezugspunkte mit (P0)= 0:
• Erdoberfläche (Äquipotentialfläche, siehe Folie 3-18)
• "Masse" in Schaltungen, z.B. Minuspol der Batterie oder Gehäuse
• eine gedachte unendliche ferne Hülle
Folie 3-16
Elektrostatisches Feld
Berechnung des elektrostatischen Potentials
P0
W12 = W10 + W02
P1
P2
ϕ1
r r
r r
= Q ∫ E ⋅ ds + Q ∫ E ⋅ ds
P0
ϕ2
P2
P1
P0
⎛ P0 r r P0 r r ⎞
= Q⎜ ∫ E ⋅ ds − ∫ E ⋅ ds ⎟ ≡ Q ⋅ (ϕ1 − ϕ 2 )
⎜P
⎟
P2
⎝ 1
⎠
Es folgt: Das elektrostatische Potential (P) an einem Punkt P ist der Quotient
aus der Arbeit, die nötig ist, um eine Ladung Q von einem Punkt P0 mit dem
Bezugspotential (P0)=0 zum Punkt P zu bringen, und der Ladung Q:
Pi
r r
r r
W0i
ϕ i = ϕ ( Pi ) = ∫ E ⋅ ds = − ∫ E ⋅ ds = −
Q
Pi
P0
P0
Folie 3-17
Elektrostatisches Feld
Äquipotentialflächen
Auf Äquipotentialflächen ist
das Potential konstant. Bewegt
man Ladungen entlang dieser
Flächen, so ändert sich ihre
potentielle Energie nicht.
Die elektrischen Feldlinien
stehen senkrecht auf den
Äquipotentialflächen.
Äquipotentiallinien sind die
Schnittlinien der Äquipotentialflächen mit der Zeichenebene.
Zeichenkonvention:
Der Abstand zwischen jeweils
benachbarten Linien entspricht
einer festen Potentialdifferenz.
(Potential einer Punktladung Q:)
Q
1
⋅
ϕ (r) =
4πε 0 r
Folie 3-18
Elektrostatisches Feld
Elektrische Spannung
Die Potentialdifferenz zwischen zwei beliebigen Punkten P1 und P2 in einem
elektrischen Feld E wird als elektrische Spannung U bezeichnet.
r r
U12 = ϕ ( P1 ) − ϕ ( P2 ) = ∫ E ⋅ ds
P2
P1
Die Einheit der elektrischen Spannung ist das Volt: 1 V = 1 J/As = 1 kg m2/As3
(nach Alessandro Giuseppe Antonio Anastasio Graf von Volta, 1745–1827).
Die potentielle Energie, die eine Ladung Q im Punkt P1 gegenüber dem Punkt
P2 besitzt, ist gegeben durch das Produkt aus der Spannung zwischen P1 und
P2 und der Ladung Q:
W12 = Q ⋅ U12
Folie 3-19
Elektrostatisches Feld
Elektrisches Feld geladener Platten
Wenn der Abstand der
Platten klein ist im Vergleich
zu den Abmessungen der
Platten, ist das elektrische
Feld, wie in b) skizziert,
nahezu homogen, d.h. die
elektrische Feldstärke ist in
Betrag und Richtung überall
gleich. Außerdem ist das
Streufeld am Rande der Platten und im Außenraum vernachlässigbar klein.
gegeben:
A = Innenfläche einer Platte
Q = Ladung auf einer Platte
gesucht:
E = Feldstärke (Betrag des
homogenen elektrischen Feldes)
Folie 3-20
Elektrostatisches Feld
Elektrisches Feld geladener Platten
+
+ + + +
...
Die elektrische Feldstärke kann berechnet werden,
indem die Fläche der ebenen Platte als kleiner
Ausschnitt der Oberfläche einer sehr großen Kugel
(Radius r
∞) aufgefasst wird.
+
+
+
+
+
+
+
Plattenfläche A
+
Das Feld außerhalb einer Kugel mit gleichmäßig
auf A: Ladung Q
+
über die Oberfläche verteilter Ladung ist das
+
gleiche, als wäre die gesamte Ladung im
+
Mittelpunkt der Kugel konzentriert (Punktladung!).
+
Die äquivalente Mittelpunktladung ist:
+
+
2
...
Kugeloberfläche
4π r
QKugel = Q ⋅
es folgt:
A
= Q⋅
A
1 QKugel
1 Q ⋅ 4π r 2 1 Q
E=
=
=
2
2
4πε 0 r
4πε 0 A ⋅ r
ε0 A
Folie 3-21
Elektrostatisches Feld
Spannung zwischen geladenen Platten
Da das Feld homogen ist, berechnet sich die Spannung zu:
r r d
∫ E ⋅ ds = ∫ Edx = Ed
rechte Platte
U=
linke Platte
Mit
1 Q
E=
ε0 A
0
ergibt sich
1 d
U=
Q
ε0 A
Die Spannung U ist also nur von den geometrischen Abmessungen (Fläche A
und Plattenabstand d) sowie der Ladung Q abhängig.
Folie 3-22
Elektrostatisches Feld
Influenz
In das homogene Feld zwischen den beiden
Platten bringen wir einen aus zwei dünnen
leitenden Scheiben bestehenden ungeladenen
Körper.
Auf die Ladungsträger in den Scheiben werden
infolge des elektrischen Feldes Kräfte ausgeübt.
Die freien Elektronen werden zur positiven
Platte hin angezogen, auf der gegenüberliegenden Seite entsteht ein entsprechender
Elektronenmangel. Man spricht von
influenzierten Ladungen.
(Nachweisbar durch getrenntes Herausnehmen
der Scheiben und Messung der Ladungen).
Das elektrische Feld der influenzierten Ladungen kompensiert das äußere
Feld im Innern des Leiters. Der Leiter ist im Innern feldfrei.
Folie 3-23
Elektrostatisches Feld
Nichtleitende Materie im elektrischen Feld
Bringt man ein nichtleitendes homogenes Material (ein Dielektrikum) in ein
elektrisches Feld ein, so wird die elektrische Feldstärke geschwächt.
Im Versuch mit den geladenen Platten sinkt bei gleichbleibender Ladung die
Spannung zwischen den Platten ab.
Vakuum
Nichtleiter
Leiter
Folie 3-24
Elektrostatisches Feld
Dielektrische Polarisation
Die Ursache für dieses Verhalten liegt im inneren Aufbau des isolierenden
Materials. Im Gegensatz zu einem Leiter sind die Elektronen zwar nicht frei
beweglich, dennoch tritt eine Ladungsverschiebung innerhalb der atomaren
Strukturen auf. Infolge des von außen angelegten elektrischen Feldes wirken
Kräfte auf die Ladungsträger, die dazu führen, dass Atome bzw. Moleküle in
der einen Richtung negativ und in der entgegengesetzten Richtung positiv
polarisiert werden.
Die Ursachen für die Polarisation sind vielfältig.
Ein Beispiel: Verschiebungspolarisation, Elektronenpolarisation
Folie 3-25
Elektrostatisches Feld
Nichtleitende Materie im elektrischen Feld
1 Q
E=
ε0 A
im Vakuum
1 Q
E=
,εr > 1
ε 0ε r A
im Dielektrikum
E=0
im Leiter
Folie 3-26
Elektrostatisches Feld
Dielektrizitätszahl
Stoff
r
für verschiedene Materialien
r
Stoff
r
Trockene Luft
1,000594
Polyäthylen
2,3
Bariumtitanat
1000 ... 4000
Polystyrol
2,3 ... 2,7
Bernstein
2,8
Porzellan
6,0 ... 8,0
Gummi
2,6
Quarz
3,5 ... 4,5
Hartpapier
5,0 ... 6,0
Quarzglas
4
Papier
1,2 ... 3,0
Destilliertes Wasser
81
Folie 3-27
Elektrostatisches Feld
Kapazität
Wir haben bereits beim Plattenkondensator gesehen, dass die elektrische
Spannung U zwischen den Platten der gespeicherten Ladung ±Q
proportional ist. Diese Proportionalität gilt unabhängig von der Geometrie
der Anordnung.
Q~U
Q = CU
Unter der Kapazität C versteht man das Verhältnis aus der aufgenommenen
Ladung Q zu der angelegten Spannung U. Sie ist ein Maß für die Fähigkeit
eines Körpers, Ladungen zu speichern.
Die Einheit der Kapazität ist das Farad: 1 F = 1 As/V = 1 C/V.
(Nach Michael Faraday, 1791-1867).
Kondensatoren sind Bauelemente zur Ladungsspeicherung mit definierter
Kapazität C.
Schaltsymbol des Kondensators:
Folie 3-28
Elektrostatisches Feld
Kapazität des Plattenkondensators
U=
1 d
Q
ε 0ε r A
A⎞
⎛
Q = ⎜ ε 0ε r ⎟U
d⎠
⎝
Die Kapazität des Plattenkondensators berechnet
sich zu
A
A
C = ε 0ε r = ε
d
d
Die Kapazität des (idealen) Plattenkondensators hängt also nur von der
Fläche der Platten, dem Abstand der Platten und von den Materialeigenschaften ab, nicht aber von der auf den Platten befindlichen
Ladung.
Folie 3-29
Elektrostatisches Feld
Parallelschaltung von Kondensatoren
Alle oberen und alle unteren Kondensatorplatten liegen jeweils auf gleichem
Potential, d.h., die Spannung U ist für alle Kondensatoren gleich. Für den
Gesamtkondensator (Ersatzschaltbild) muss Qges = CgesU gelten.
n
n
n
k =1
k =1
k =1
Qges = ∑ Qk = ∑ CkU = U ∑ Ck = U Cges
n
Cges = ∑ Ck
k =1
Folie 3-30
Elektrostatisches Feld
Reihenschaltung von Kondensatoren
Die gesamte an den Eingangsanschlüssen vorhandene Spannung
(Potentialdifferenz) Uges setzt sich als Summe der Teilspannungen über den
einzelnen Kondensatoren zusammen. Bringt man auf die beiden äußeren, mit
den Anschlussklemmen verbundenen, Platten eine Ladung ±Q, dann werden
auf allen inneren Kondensatoren ebenfalls Ladungen ±Q influenziert.
n
Q
1
1
= ∑U k = ∑
= Q∑
=Q
Cges
k =1 Ck
k =1 Ck
k =1
n
U ges
n
n
1
1
=∑
Cges k =1 Ck
Folie 3-31
Elektrostatisches Feld
Praktische Ausführungsformen von Kondensatoren
Vielschichtkondensator
Die Schichten wirken wie eine Parallelschaltung von Kondensatoren.
Besteht jeder Kondensatoranschluss aus n Platten, dann sind 2n-1
Kondensatoren parallel geschaltet.
Folie 3-32
Elektrostatisches Feld
(Praktische Ausführungsformen von Kondensatoren)
Drehkondensator
In Abhängigkeit von der
Rotorposition ändert sich
die überdeckte Fläche und
damit auch die Kapazität.
Wickelkondensator
Zwei Metallfolien,
dazwischen zwei Kunststofffolien. Durch das Aufwickeln
tragen beide Seiten der
Metallfolie zur Kapazität bei.
Folie 3-33
Elektrostatisches Feld
Im Kondensator gespeicherte Energie
Die in einem Kondensator gespeicherte elektrische Energie ist proportional
zum Produkt aus der Kapazität C und dem Quadrat der angelegten
Spannung U.
1
1
2
We = CU = QU
2
2
Diese Beziehung ist unabhängig von der speziellen Geometrie des
Kondensators. (Alle geometrischen Einflüsse sind in der Kapazität C
berücksichtigt).
Bemerkung: W = Q ·U gilt nur, wenn die Spannung konstant ist. Wird
elektrische Arbeit verrichtet, sinkt die Spannung durch Entladung
(dies wird im folgenden Abschnitt behandelt).
Folie 3-34
Technische Informatik I
Prof. Dr. Martin Radetzki
Universität Stuttgart
Kapitel 4
Elektrischer Strom
und elektrische Netzwerke
Folie 4-1
Elektrischer Strom und elektrische Netzwerke
Elektrischer Strom
Elektrode 1
+Q
1
r
E
Elektrode 2
-Q
2<
1
Zwischen zwei Elektroden mit den Ladungen +Q und –Q besteht ein
elektrisches Feld. Die Elektrode 1 liegt auf dem Potential 1, die Elektrode 2
liegt auf dem Potential 2. Zwischen den Elektroden besteht demnach die
Spannung U12 = 1– 2.
Folie 4-2
Elektrischer Strom und elektrische Netzwerke
(Elektrischer Strom)
Elektrode 1
I
+Q
Verbindet man die Elektroden durch eine
leitende Verbindung, in der sich die
Elektronen frei bewegen können, so findet
ein Ladungsausgleich statt, und zwar
solange, bis zwischen den Elektroden keine
Spannung mehr vorhanden ist.
Elektrode 2
-Q
Die Bewegung der Ladungsträger bezeichnet man als elektrischen Strom.
Definition der Stromrichtung:
Ein positiver Strom fließt von der Elektrode höheren Potentials zur Elektrode
niedrigeren Potentials (technische Stromrichtung).
Die Elektronen bewegen sich entgegengesetzt zur technischen Stromrichtung!
Folie 4-3
Elektrischer Strom und elektrische Netzwerke
Elektrische Stromstärke
Die elektrische Stromstärke ist die Ladungsmenge Q, die in einer Zeitspanne
t durch die leitende Verbindung von der Elektrode 1 zur Elektrode 2 fließt.
ΔQ
I=
Δt
Die elektrische Stromstärke ist eine SI-Basiseinheit. Ihre Einheit ist das
Ampere (nach André Marie Ampère, 1775 – 1836).
SI-Basiseinheit der Stromstärke: [I] = A = Ampere
Wenn die Stromstärke zeitlich nicht konstant ist, dann gibt obige Beziehung
lediglich die mittlere Stromstärke während des Zeitabschnittes t an. Die
momentane Stromstärke zu einem Zeitpunkt t erhält man als
Δ Q dQ
=
I (t ) = lim
Δt →0 Δt
dt
Folie 4-4
Elektrischer Strom und elektrische Netzwerke
Ladungsträgerbewegung im Leiter
Bei Metallen sind die Elektronen auf der äußersten Schale nur sehr schwach
gebunden. Sie können sich quasi frei innerhalb des Atomverbandes bewegen.
Ohne äußere Einflüsse bewegen sich die Atome ungeordnet mit gleicher
Wahrscheinlichkeit in alle Richtungen. Der Mittelwert über alle Bewegungen
ist Null, das heißt, ein elektrischer Strom ist nicht feststellbar.
Folie 4-5
Elektrischer Strom und elektrische Netzwerke
(Ladungsträgerbewegung im Leiter)
In einem elektrischen Feld
erfahren die Elektronen
eine Kraft und damit eine
permanente Beschleunigung entgegengesetzt zum
Feldstärkevektor. Ihre
Bewegung wird immer
wieder durch Stöße mit den
ortsfesten Atomen und an
den Unregelmäßigkeiten im
Gitteraufbau unterbrochen.
An den Stoßstellen werden die Elektronen gestreut, d.h., sie werden
abgebremst und ändern ihre Richtung, wobei sie kinetische Energie verlieren.
Im Mittel erlangen sie aber durch das elektrische Feld eine mittlere
r
Driftgeschwindigkeit:
r
v e = − μe E µe: Beweglichkeit der Elektronen
Folie 4-6
Elektrischer Strom und elektrische Netzwerke
Stromdichte
Wir betrachten einen Ausschnitt
aus einem stromführenden Leiter.
Der Leiterquerschnitt habe die
Fläche A. Im Leiter befinden
sich positive Ladungsträger mit
einer Driftgeschwindigkeit vx in xRichtung.
Die Stromdichte J gibt den Strom bezogen auf die
durchströmte Fläche an. Sie hat die Einheit A/m2:
Die Raumladungsdichte gibt die pro Volumenelement zum Ladungstransport zur Verfügung stehende
Ladung an. Sie hat die Einheit As/m3.
J=
ΔQ
ΔI
ΔQ Δx
=
=
⋅
= ρ v , vektoriell:
ΔA ΔAΔt ΔAΔx Δt
ΔI
J=
ΔA
ΔQ
ρ=
ΔV
r
r
J = ρv
Folie 4-7
Elektrischer Strom und elektrische Netzwerke
Ohm'sches Gesetz in differentieller Form
Bezeichnen wir mit n die Anzahl der freien Ladungsträger pro Volumen
(Ladungsträgerkonzentration), dann lässt sich die zum Ladungstransport
zur Verfügung stehende Raumladungsdichte ausdrücken als
ρ = − en
r
r
r
r
Mit v e = − μe E und J = ρ v ergibt sich für die Stromdichte:
r
r
r
J = neμe E = κ E
Die Größe heißt
spezifische Leitfähigkeit
und hat die Einheit
[
J ] A/m
[κ ] = =
[E ] V/m
1
=
m
ACHTUNG:
und
2
ρR =
R
1
κ
Ohm'sches Gesetz in
differentieller Form
Der Kehrwert von heißt
spezifischer Widerstand
und hat die Einheit
[ρ ] = [E ] = V/m2
[J ] A/m
= m
sind grundverschiedene Größen!
Folie 4-8
R
Elektrischer Strom und elektrische Netzwerke
Temperaturabhängigkeit des spezifischen Widerstands
Der spezifische Widerstand ist im Allgemeinen temperaturabhängig. Für die
meisten technischen Anwendungen kann man die Temperaturabhängigkeit
durch eine lineare Näherung hinreichend genau beschreiben.
ρ R (T ) = ρ R (20°C) ⋅ [1 + α (T − 20°C)]
kurz:
ρ R (T ) = ρ R (20°C) ⋅ [1 + α ΔT ]
Ursache für die Temperaturabhängigkeit:
Bei höherer Temperatur schwingen die Atome im Gitter stärker; die Wahrscheinlichkeit, dass Elektronen mit Atomen zusammenstoßen, steigt. Daher ist
bei allen reinen Metallen der Temperaturkoeffizient positiv und liegt in etwa
derselben Größenordnung. Bei Legierungen dominiert der Effekt, dass Elektronen am unregelmäßigen Gitteraufbau gestreut werden. Der spezifische Widerstand von Legierungen ist daher grundsätzlich größer. Die Bewegungen der
Gitteratome spielen bei Legierungen für die Streuung der Elektronen kaum eine
Rolle, so dass der Temperaturkoeffizient deutlich geringer ist.
Folie 4-9
Elektrischer Strom und elektrische Netzwerke
Leitfähigkeit, Widerstand und Temperaturkoeffizient
verschiedener Materialien bei 20°C
Leiter
Aluminium
Chromnickel
· m-1 mm2
35
0,91
R
·m
-1mm-2
· 103 K
0,0287
3,8
1,1
0,2
Eisen
10
0,10
6,1
Gold
44
0,022
3,9
Graphit
0,125
8
-0,2
Konstantan*)
2
0,5
0,0035
Manganin*)
2,3
0,43
0,02
Kupfer
56
0,0178
3,9
Messing
12,5
0,08
1,5
Silber
62,5
0,016
3,8
Wolfram
18
0,055
4,1
*) Konstantan:
Manganin:
Legierung aus 54% Cu, 45%Ni, 1% Mn
Legierung aus 84% Cu, 4% Ni, 12% Mn
Folie 4-10
Elektrischer Strom und elektrische Netzwerke
Strom und Spannung an einem stromdurchflossenen Leiter
r r
E, J
Für die Spannung gilt:
r r
U = ϕ 1 − ϕ 2 = ∫ E ds = E ⋅ l
U
Mit
I
E = J = ρR J = ρR
κ
A
1
l
U = ρR I
A
ergibt sich
Ohm'sches Gesetz in
integraler Form!
l
R = ρR
A
Folie 4-11
Elektrischer Strom und elektrische Netzwerke
Ohm'sches Gesetz in integraler Form
Das Ohm'sche Gesetz (nach Georg Simon Ohm, 1789 – 1854) beschreibt eine
empirische Erfahrung:
Die an einem Leiter anliegende Spannung ist der durch den Leiter fließenden
Stromstärke proportional.
U
U = R⋅I
R
I
(Schaltsymbol eines el. Widerstandes)
Der Proportionalitätsfaktor R heißt elektrischer Widerstand.
Er hat die Einheit [R] = V/A = = Ohm.
In vielen Fällen bietet es sich an, dass man nicht den
Widerstand, sondern seinen Kehrwert G = 1/R verwendet.
G heißt elektrischer Leitwert und besitzt die Einheit 1/
= A/V.
1
G=
R
Folie 4-12
Elektrischer Strom und elektrische Netzwerke
(Ohm'sches Gesetz in integraler Form)
Temperaturabhängigkeit des elektrischen Widerstands:
R(T ) = ρ R ( 20°C) ⋅
l
⋅ [1 + α (T − 20°C)]
A
R(T ) = R( 20°C) ⋅ [1 + α (T − 20°C)]
Bsp.:
Ein Kupferdraht habe bei 20°C
einen Widerstand von 1 . Wie
groß ist sein Widerstand bei
100°C?
1
⎡
⎤
R(100°C) = R( 20°C) ⋅ ⎢1 + 3,9 3 ⋅ 80K ⎥ ≈ 1,31Ω
10 K
⎣
⎦
Folie 4-13
Elektrischer Strom und elektrische Netzwerke
Leistung des elektrischen Stroms
Beim Transport von Ladung durch einen Leiter infolge eines elektrischen
Feldes wird an den Ladungsträgern Arbeit verrichtet. Diese Energie wird dem
Energieinhalt des elektrischen Feldes entnommen und im Leiter als
Wärmeenergie umgesetzt.
Die Leistung gibt die verrichtete Arbeit pro
Zeiteinheit an.
Sie hat die Einheit [P] = VA = Watt (W)
(nach James Watt, 1736 – 1819).
ΔW dW
=
P(t ) = lim
Δt →0 Δt
dt
Für einen elektrischen Widerstand R gilt:
U
1
R
I
2<
1
2
U
P = UI = I 2 R =
R
Folie 4-14
Elektrischer Strom und elektrische Netzwerke
Festwiderstände - Bauformen
Folie 4-15
Elektrischer Strom und elektrische Netzwerke
Weitere Widerstandsformen
Einstellbare Widerstände (Potentiometer):
Ein Schleifkontakt wird über das nicht isolierte Widerstandsmaterial
bewegt, und damit ein bestimmter Bruchteil des insgesamt möglichen
Widerstands abgegriffen.
Bauformen:
• Schiebewiderstand (linear angeordneter Widerstandskörper)
• Drehwiderstand (ringförmig angeordneter Widerstandskörper)
Temperaturabhängige Widerstände
• NTC (negative temperature coefficient), oder Heißleiter: er hat bei
Raumtemperatur einen hohen Widerstand, im Betrieb erhitzt er sich und
hat einen niedrigen Widerstand. (Verwendung beispielsweise zur
Begrenzung von Einschaltströmen).
• PTC (positive temperature coefficient), oder Kaltleiter:
Temperaturverhalten genau umgekehrt wie beim NTC.
Folie 4-16
Elektrischer Strom und elektrische Netzwerke
Elektrische Netzwerke
Zur Beschreibung elektronischer Schaltungen verwendet man elektrische
Netzwerke. Man verwendet für die elektronischen Bauelemente einfache
Modelle (Ersatzschaltbilder), in denen das Verhalten der realen Bauelemente
durch integrale Größen wie z. B. Widerstand R und Kapazität C modelliert
werden.
Ein zentraler Begriff bei der Behandlung von Netzwerken ist der des
Zweipols. Unter einem Zweipol versteht man ein Bauelement mit zwei
Anschlussklemmen. Aus Sicht des Netzwerkes spielt nur noch das
Klemmenverhalten (d. h. der Zusammenhang zwischen Strom und
Spannung) am betreffenden Bauelement eine Rolle.
Zur vollständigen Beschreibung eines elektrischen Netzwerkes (Schaltkreis)
kommt zum Klemmenverhalten der einzelnen Bauelemente auch ihre
Verknüpfung hinzu (Schaltungstopologie).
Folie 4-17
Elektrischer Strom und elektrische Netzwerke
Schaltbilder
Die grafische Darstellung von Netzwerken bezeichnet man als Schaltbilder.
Zur Darstellung der Bauelemente werden Schaltsymbole verwendet. Die
leitenden Verbindungen zwischen den Bauelementen werden als ideale, d.h.
widerstandslose, Leiter angesehen und spielen bei der Rechnung keine Rolle.
Kreuzen sich Verbindungslinien, so
gelten sie nur als verbunden, wenn dies
durch einen Punkt ("Lötpunkt")
markiert ist. Diese Verbindungspunkte
heißen Knoten des Netzwerkes. Die
Bauelemente zwischen den Knoten
stellen zusammen mit ihren leitenden
Verbindungen Zweige des Netzwerks
dar.
Folie 4-18
Elektrischer Strom und elektrische Netzwerke
Zählpfeile
Strom und Spannung sind skalare Größen. Dennoch werden ihnen in
Schaltungen Pfeile zugeordnet. Diese Pfeile dienen der Zählweise und dürfen
nicht mit Vektoren verwechselt werden.
Ein Spannungspfeil in Richtung der elektrischen Feldstärke zeigt positive
Spannungen an. Er zeigt von einem Punkt höheren Potentials zu einem Punkt
niedrigeren Potentials.
Ein Strompfeil in Bewegungsrichtung der positiven Ladungsträger zeigt
positive Ströme an. Er wird in die Verbindungslinie eingezeichnet, die den
Strom führt.
U
1
R
I
2
<
1
für U > 0
Folie 4-19
Elektrischer Strom und elektrische Netzwerke
Spannungs- und Stromquellen
Ein Kondensator produziert nur solange einen Strom, bis seine gesamte
Ladung abgeflossen ist. Als Gleichstromquelle ist er nicht geeignet.
Eine Gleichstromquelle muss die von den Platten abfließenden Ladungen
immer wieder nachliefern.
Folie 4-20
Elektrischer Strom und elektrische Netzwerke
Ideale Spannungs- und Stromquellen
I
U
Gleichspannung
i(t)
u(t)
Gleichstrom
zeitlich veränderliche Spannung
zeitlich veränderlicher Strom
Bei einer idealen Spannungsquelle hängt die Ausgangsspannung nicht vom
angeschlossenen Netzwerk ab, (sondern nur der gelieferte Strom).
Bei einer idealen Stromquelle hängt der Ausgangsstrom nicht vom
angeschlossenen Netzwerk ab, (sondern nur die gelieferte Spannung).
Folie 4-21
Elektrischer Strom und elektrische Netzwerke
Zählpfeilsysteme
An Verbrauchern werden Strom und Spannung in der gleichen Richtung
gezählt (Verbraucherzählpfeilsystem).
An Spannungs- und Stromquellen sind Spannung und Strom entgegengesetzt
gerichtet (Generatorzählpfeilsystem).
Hintergrund: Quellen liefern Energie, Verbraucher nehmen sie auf.
Folie 4-22
Elektrischer Strom und elektrische Netzwerke
Netzwerkanalyse
Ziel der Netzwerkanalyse ist die Berechnung aller Ströme und Spannungen
an den einzelnen Bauelementen.
Bsp.: Wie groß sind die Spannungen an den Widerständen R1 bis R5 und wie
groß sind die Ströme durch die Widerstände? Wie groß ist der Strom, den die
Gleichspannungsquelle liefert?
Das Ohm'sche Gesetz alleine reicht für die Beantwortung dieser Fragen nicht
aus.
Folie 4-23
Elektrischer Strom und elektrische Netzwerke
Kirchhoff'sche Gleichungen
Maschenregel
r r
∫ E ⋅ ds = 0
⇒ U R1 + U R 3 − U R 4 = 0
∑U = 0
Masche
Die Summe aller Spannungen beim Umlauf in einer
geschlossenen Masche ist Null.
Spannungen, deren Zählpfeil dabei entgegen der
Umlaufrichtung verläuft, werden negativ gezählt.
Folie 4-24
Elektrischer Strom und elektrische Netzwerke
Kirchhoff'sche Gleichungen: Knotenregel
Knotenregel
Ein Schaltungsknoten
hat keine Kapazität.
Alle Ladung, die in ihn
hineinfließt, muss auch
wieder aus ihm
herausfließen.
⇒
I R1 − I R 3 − I R 5 = 0
∑I = 0
Knoten
Die Summe aller in einen Knoten hineinfließenden
Ströme ist Null.
Ströme, deren Zählrichtung vom Knoten wegzeigt,
werden dabei negativ gezählt.
Folie 4-25
Elektrischer Strom und elektrische Netzwerke
Reihenschaltung von Widerständen
Alle Widerstände werden vom selben Strom
durchflossen. Anwendung der Maschenregel
liefert:
n
n
U ges = ∑U k =∑ Rk I = Rges I
k =1
k =1
n
Rges = ∑ Rk
k =1
n
1
1
=∑
Gges k =1 Gk
Folie 4-26
Elektrischer Strom und elektrische Netzwerke
Parallelschaltung von Widerständen
An allen Widerständen liegt dieselbe Spannung.
Anwendung der Knotenregel liefert:
n
I ges
n
U
U
= ∑ I k =∑
=
Rges
k =1
k =1 Rk
n
1
1
=∑
Rges k =1 Rk
n
Gges = ∑ Gk
k =1
Folie 4-27
Elektrischer Strom und elektrische Netzwerke
Spannungsteiler
Mit einer Reihenschaltung
von Widerständen kann man
eine gegebene Spannung U
mit hoher Genauigkeit in
kleinere Teilspannungen
aufteilen.
Es gilt:
U1 R1
=
U 2 R2
und
U2
R2
=
U
R1 + R2
Folie 4-28
Elektrischer Strom und elektrische Netzwerke
Spannungsabfall am Widerstand
Die an einem Widerstand entstehende Teilspannung wird als Spannungsabfall
bezeichnet.
Bsp.: Potentialverlauf an einer Reihenschaltung. Definiert man das
Bezugspotential = 0 für die rechte Klemme (Minuspol der Spannungsquelle),
dann besitzt die linke Klemme das Potential = U. Innerhalb der Widerstände
nimmt das Potential linear ab.
Folie 4-29
Elektrischer Strom und elektrische Netzwerke
Belasteter Spannungsteiler
Schließt man an den
Spannungsteiler einen
Verbraucher an, zum
Beispiel ein Spannungsmessgerät (Voltmeter), so
entspricht der gemessene
Wert nicht mehr dem oben
berechneten, d.h.
U2
R2
≠
U
R1 + R2
In die Berechnung muss noch der Widerstand des Verbrauchers (hier
der Innenwiderstand des Messgerätes) berücksichtigt werden.
Im Beispiel:
U2
R2 ⋅ RM
=
U
R1 (R2 + RM ) + R2 ⋅ RM
Folie 4-30
Elektrischer Strom und elektrische Netzwerke
(Belasteter Spannungsteiler)
U2
R2 ⋅ RM
=
U
R1 (R2 + RM ) + R2 ⋅ RM
Auswertung des Beispiels
für (R1+R2) = 10 k ,
0 ≤ R2 ≤ 10 k
und
verschiedene Werte von RM.
Man sieht: mit kleinerem Innenwiderstand RM geht die Linearität
zwischen der Potentiometerstellung und der Ausgangsspannung verloren.
Folie 4-31
Elektrischer Strom und elektrische Netzwerke
Stromteiler
Mit einer Parallelschaltung von
Widerständen kann ein
Gesamtstrom I in mehrere
Teilströme aufgeteilt werden.
Es gilt:
I1 R2 G1
=
=
I 2 R1 G2
und
I2
R1
G2
=
=
I
R1 + R2 G1 + G2
Folie 4-32
Elektrischer Strom und elektrische Netzwerke
Reale Spannungsquelle - Ersatzschaltbild
Wird eine reale Spannungsquelle durch
einen Verbraucher belastet, dann ruft
der Strom einen Spannungsabfall und
damit interne Verluste hervor. Man
modelliert dies durch einen mit der
Quellenspannung U0 in Reihe
liegenden Innenwiderstand Ri.
Man kann die Quelle vollständig
charakterisieren durch ihre Leerlaufspannung und ihren Kurzschlussstrom:
Leerlaufspannung:
U = UL = U0
Kurzschlussstrom:
IK = U0 / Ri
Im Kurzschlussbetrieb werden beide Klemmen leitend verbunden. Die
gesamte Leistung wird dann am Innenwiderstand umgesetzt!
Folie 4-33
Elektrischer Strom und elektrische Netzwerke
Reale Stromquelle - Ersatzschaltbild
Wird eine reale Stromquelle durch
einen Verbraucher belastet, dann ruft
die Spannung über dem Verbraucher
eine Reduzierung des Stroms und
damit interne Verluste hervor. Man
modelliert dies durch einen parallel
zum Quellenstrom I0 liegenden
Innenwiderstand Ri.
Man kann die Quelle vollständig
charakterisieren durch ihre Leerlaufspannung und ihren Kurzschlussstrom:
Leerlaufspannung:
UL = I0 Ri
Kurzschlussstrom:
I = IK = I0
Im Leerlaufbetrieb ist kein Verbraucher angeschlossen. Die gesamte
Leistung wird dann am Innenwiderstand umgesetzt!
Folie 4-34
Elektrischer Strom und elektrische Netzwerke
Äquivalente Quellen
Spannungs- und Stromquelle können ineinander umgerechnet werden. Dazu
muss sichergestellt werden, dass beide Quellen die gleiche Leerlaufspannung
und den gleichen Kurzschlussstrom aufweisen. Beide Forderungen sind
erfüllt, wenn für Quellenspannung und Quellenstrom gilt:
U0 = I0 Ri
Folie 4-35
Elektrischer Strom und elektrische Netzwerke
Überlagerungsprinzip
Enthält eine Schaltung mehrere Quellen, dann können die Ströme und
Spannungen in den einzelnen Zweigen durch Überlagerung von
Teillösungen berechnet werden. Voraussetzung: lineare Beziehungen
zwischen Strom und Spannung an den Netzwerkelementen.
Berechnung von Teillösungen:
• nur eine einzige Quelle wird betrachtet
• alle anderen Stromquellen werden durch Leerlauf ersetzt (I = 0)
• alle anderen Spannungsquellen werden durch Kurzschluss ersetzt (U = 0)
Berechnung der Gesamtlösung aus den Teillösungen:
• alle Teilströme eines Zweiges werden addiert
• alle Teilspannungen eines Zweiges werden addiert
Folie 4-36
Elektrischer Strom und elektrische Netzwerke
(Überlagerungsprinzip) Beispiel
Bsp.:
Wie groß ist der Strom I2 durch R2?
Folie 4-37
Elektrischer Strom und elektrische Netzwerke
(Überlagerungsprinzip Beispiel)
Teillösung a)
Setze I0 = 0,
d.h., ersetze die Stromquelle
durch Leerlauf.
U0
I 2a =
R1 + R2
Teillösung b)
Setze U0 = 0,
d.h., ersetze die Spannungsquelle
durch Kurzschluss.
R1 I 0
I 2b =
R1 + R2
Folie 4-38
Elektrischer Strom und elektrische Netzwerke
(Überlagerungsprinzip Beispiel)
Zusammengesetzte Gesamtlösung:
U 0 + R1 I 0
I 2 = I 2a + I 2b =
R1 + R2
Folie 4-39
Elektrischer Strom und elektrische Netzwerke
Aufladung eines Kondensators
R
t=0
i(t)
U0
u(t)
Für die Ladung q(t) am Kondensator gilt:
Mit
i (t ) =
Der Kondensator sei
zunächst ungeladen. Zum
Zeitpunkt t=0 werde der
Schalter geschlossen.
dq
dt
folgt daraus:
Anwendung der Maschenregel:
und damit die Differentialgleichung:
C
Gesucht:
Das zeitliche Verhalten der
Spannung u(t) und des
Stromes i(t) in der
gezeigten Schaltung.
q(t ) = Cu(t )
du
dt
Ri (t ) + u(t ) = U 0
i (t ) = C
du
RC
+ u(t ) = U 0
dt
Folie 4-40
Elektrischer Strom und elektrische Netzwerke
(Aufladung eines Kondensators)
du
+ u(t ) = U 0
dt
Lineare inhomogene Differentialgleichung:
RC
Zugehörige homogene Differentialgleichung:
du
RC
+ u (t ) = 0
dt
Lösungsansatz (z.B. durch Separation der Variablen):
u(t ) = K ⋅ e
−
t
RC
Dabei ist K eine aus den Randbedingungen
noch zu bestimmende Konstante.
Eine offensichtliche spezielle Lösung der inhomogenen
Differentialgleichung ist:
u(t ) = U 0
Damit ergeben sich alle Lösungen zu
u(t ) = K ⋅ e
−
t
RC
+ U0
Folie 4-41
Elektrischer Strom und elektrische Netzwerke
(Aufladung eines Kondensators)
Bestimmung der Konstanten K aus den Randbedingungen:
Zum Zeitpunkt t=0 wird der Schalter geschlossen. Der Kondensator soll zu
diesem Zeitpunkt noch ungeladen sein, d.h. u(0) = 0.
Einsetzen in u(t ) = K ⋅ e
−
t
RC
+ U0
ergibt K = – U0
Damit ergibt sich für die Spannung am Kondensator:
t
−
⎛
⎞
RC ⎟
⎜
u (t ) = U 0 ⎜1 − e ⎟
⎝
⎠
du
Für den Strom i(t) erhält man aus i (t ) = C
dt
t
U 0 − RC
U0
e
i (t ) =
Anfangsstrom: i (0) =
R
R
Folie 4-42
Elektrischer Strom und elektrische Netzwerke
(Aufladung eines Kondensators)
u(t)
U0
t
−
⎛
⎞
RC
u(t ) = U 0 ⎜⎜1 − e ⎟⎟
⎝
⎠
63% ·U0
U0
t
t
du U 0 − RC
=
e
dt RC
=RC
i(t)
U0
R
t
Die Zeitkonstante = RC ist ein Maß dafür, wie schnell die Kondensatorspannung ihren Endwert erreicht. Nach t = 1 erreicht sie ca. 63% ihres
Endwertes; nach t = 3 sind es bereits ca. 95%.
Folie 4-43
Technische Informatik I
Prof. Dr. Martin Radetzki
Universität Stuttgart
Kapitel 6
Halbleiterbauelemente
Folie 7-1
Halbleiterbauelemente
Mikroelektronik – 1970 bis heute
Keine andere Technologie macht eine so rasante Entwicklung durch wie die
Mikroelektronik – und das seit vielen Jahrzehnten!
Intel 1101 256-bit SRAM
Intel 4004 4-bit-Mikroprozessor
(1971, ca. 2500 Transistoren, ca.
100kHz, 30mm2, 4 Designer)
Folie 6-2
Halbleiterbauelemente
Prozessortechnologie 2007: Beispiel
2006: AMD Athlon-64-FX, ca. 3 000 000 kHz Taktfrequenz,
ca. 227 400 000 Transistoren, ca. 230 mm² Chipfläche.
Folie 6-3
Halbleiterbauelemente
Batch production
Auf einer Silizium-Scheibe (engl. wafer) kann eine Vielzahl von
Kopien einer Schaltung gleichzeitig hergestellt werden.
Folie 6-4
Halbleiterbauelemente
In 2003 überstieg die Zahl der jährlich produzierten Transistoren weltweit die
Marke von einer Trillion (1018) Transistoren. Damit werden im Schnitt für
jeden Menschen auf der Erde jährlich 100 Millionen Transistoren produziert.
Umsätze in der Mikroelektronik - global
(Milliarden US$)
200
150
100
50
0
1982
1984
1986
1988
1990
1992
1994
1996
1998
2000
2002
Jahr
Folie 6-5
Halbleiterbauelemente
Moore's Gesetz - Transistorzahlen
Die Anzahl der Transistoren pro CPU-Typ verdoppelt sich etwa alle 26 Monate.
Quelle: http://www.intel.com/technology/mooreslaw/
Folie 6-6
Halbleiterbauelemente
Moore's Gesetz - Taktfrequenzen
CPU-Taktfrequenzen verdoppeln sich ca. alle 34 Monate.
10,000
4004
1,000
8008
Taktfrequenz (MHz)
8080
8086
100
80286
Intel386
Intel486
10
Pentium
Pentium Pro/II/III
Pentium 4
1
1970
1975
1980
1985
1990
1995
2000
2005
Jahr
Die Transistoren werden kleiner; dadurch werden sie auch schneller,
verbrauchen weniger Energie und kosten weniger pro Stück.
Folie 6-7
Halbleiterbauelemente
Grade der Integration
Man klassifiziert integrierte Schaltungen nach dem Grad ihrer Integration,
d.h. nach der Größenordnung, in der sich die Anzahl ihrer Gatter bewegen.
Small Scale Integration
SSI
~ 10 Gatter
z.B. 7404 InverterBaustein
Medium Scale Integration
MSI
~ 1000 Gatter
z.B. 74161 ZählerBaustein
Large Scale Integration
LSI
~10.000 Gatter
z.B. einfacher 8-bitMikroprozessor
Very Large Scale
Integration
VLSI > 10.000 Gatter z.B. heutige
Prozessoren,
Systems-on-Chip
Folie 6-8
Halbleiterbauelemente
Leiter – Halbleiter - Nichtleiter
Leiter
Halbleiter
Nichtleiter (Isolatoren)
Wir betrachten im weiteren Verlauf das Element Silizium. Es ist
wirtschaftlich das bedeutendste Halbleitermaterial. Die physikalischen
Zusammenhänge sind mit nur geringen Modifikationen auf andere
Halbleitermaterialien übertragbar.
Folie 6-9
Halbleiterbauelemente
Modell des Siliziumatoms
Die erste Schale hat 2 Elektronen, die zweite 8 und die dritte ("Valenzschale")
hat 4 Elektronen (Valenzelektronen). Sie ist nicht vollständig aufgefüllt, da sie
bis zu 8 Elektronen aufnehmen kann.
Folie 6-10
Halbleiterbauelemente
Kovalente Bindung im Siliziumkristall
Jedes Siliziumatom teilt sich mit seinen vier Nachbarn je ein Elektron.
Folie 6-11
Halbleiterbauelemente
Diamantgitter
Die Struktur des Siliziumkristalls ist dieselbe wie beim Diamant (Kristall des
Kohlenstoffs). Größe der Einheitszelle (Seitenlänge): 5,43·10−10 m.
Anzahl der Atome pro Einheitszelle: 8.
Folie 6-12
Halbleiterbauelemente
Herstellung von Silizium-Wafern
Das Ausgangsmaterial für die IC-Prozesstechnologie ist monokristallines Silizium in
hoher Reinheit. Es wird mit der sogenannten
Czochralski-Methode hergestellt. Dazu wird
ein Impfkristall (engl. seed crystal) in geschmolzenes Silizium abgesenkt. Beim Herausziehen aus der Schmelze lagern sich Siliziumatome an. Es wächst ein Kristall, dessen
Gitterstruktur durch die des Impfkristalls vorgegeben ist.
Das Ziehen des Kristalls geschieht unter
Rotation. Dadurch entstehen zylinderförmige
Kristalle, die in Scheiben, sogenannte Wafer,
gesägt werden.
Folie 6-13
Halbleiterbauelemente
Energieniveaus am Beispiel des Wasserstoffatoms
n=3
–1,51eV
EH / eV
0 eV
n=∞
n=3
n=2
n=1
–13,6eV
–5 eV
n=2
–3,4eV
–10 eV
Die möglichen Energien, die das Elektron
des Wasserstoffatoms einnehmen kann,
13,6 eV
sind quantisiert:
EH = −
Für n
n
n=1
2
∞ ist das Elektron nicht mehr an den Atomkern gebunden.
Folie 6-14
Halbleiterbauelemente
Atome in Wechselwirkung miteinander
EH / eV
In einem Kristall sind die
0 eV
Atome nahe beieinander
angeordnet und stehen in
Wechselwirkung miteinander. Die Elektronen müssen dabei unterschiedliche
Energiezustände einneh- –5 eV
men (Pauli-Prinzip).
Bei N Atomen gibt es 2N
mögliche Energieniveaus
für die Elektronen.
–10 eV
Die Energieniveaus lassen
sich durch Energiebänder
veranschaulichen, in denen
sehr viele Energieniveaus
dicht beieinander liegen.
Kristall
(N Atome)
2-atomiges
Molekül
einzelnes
Atom
Atomabstand
Folie 6-15
Halbleiterbauelemente
Bändermodell
E
(Elektronenenergie)
Eoben
Leitungsband
EC
EC
EV
EV
EG
Valenzband
Eunten
x
(Ortskoordinate im Halbleiterkristall)
Bändermodell
(stark vereinfacht)
Bändermodell
Die inneren 10 Elektronen der Siliziumatome sind sehr stark an den
Atomkern gebunden. Sie werden durch die inneratomaren Kräfte kaum
gestört. Es genügt daher, die Energiezustände, die aus der Valenzschale
entstanden sind, sowie die Energiezustände, die aus den höheren
Energieniveaus des Siliziumatoms, entstanden sind, zu betrachten.
Man spricht von Valenzband und Leitungsband.
Folie 6-16
Halbleiterbauelemente
Leitungsvorgang im Halbleiterkristall
Durch thermische Anregung entstehen freie Elektronen und Löcher.
Folie 6-17
Halbleiterbauelemente
Löcherleitung
Löcher können wandern und damit Ladung transportieren.
Sie wirken wie positiv geladene Ladungsträger.
Folie 6-18
Halbleiterbauelemente
Leitungsvorgänge im Bändermodell
(Leitungsband leer)
EC
EC
EC
EV
EV
EV
(Valenzband
komplett gefüllt)
keine Leitung
thermische Erzeugung eines
Elektron-Loch-Paares
Leitungsvorgang
In einem reinen Halbleiterkristall kann elektrischer Strom fließen, wenn
thermisch erzeugte Ladungsträger zur Verfügung stehen. Elektronen und
Löcher entstehen dabei gleichzeitig ("Generation") und tragen auch
gleichzeitig zum Stromtransport bei. Elektronen fließen im Leitungsband.
Löcher fließen im Valenzband. Ein reiner Halbleiter besitzt also eine gewisse
Eigenleitfähigkeit (bei Silizium ca. 10-2/( m), Germanium ca. 1/( m)).
Elektronen und Löcher können (unter Abgabe von Energie) auch wieder
miteinander verschmelzen ("Rekombination").
Folie 6-19
Halbleiterbauelemente
Klassifizierung der Materialien: Nichtleiter und Halbleiter
Obwohl für Halbleiter entwickelt, lässt sich das Bändermodell (mit geringen
Modifikationen) auf alle Materialien übertragen. Der Hauptunterschied liegt
nicht in der Natur der Energiebänder, sondern in der Größe der Bandlücke
(engl. band gap) , d.h. im Abstand von Valenzband zu Leitungsband.
EC
EC
EG
EG
EG ~ 8 eV (SiO2)
EG ~ 5 eV (Diamant)
EV
Nichtleiter:
thermische Anregung unwahrscheinlich,
nur wenige Elektron-/Lochpaare werden
generiert.
EV
EG = 1,12 eV (Si)
EG = 0,67 eV (Ge)
(bei Zimmertemperatur)
Halbleiter:
thermische Anregung relativ leicht
möglich, eine mittlere Zahl von
Elektron-/Lochpaaren werden
generiert.
Folie 6-20
Halbleiterbauelemente
(Klassifizierung der Materialien:) Leiter
EG
EV
EC
EC
Bandabstand EG sehr klein
oder
sich überlappende Bänder
Bei Metallen ist der Bandabstand entweder sehr klein, oder Valenzband und
Leitungsband überlappen sich sogar. Eine thermische Anregung ist mit
geringem Energieaufwand möglich. Es stehen daher sehr viele Ladungsträger
zur Verfügung. Metalle sind ausgesprochen gute Leiter.
Folie 6-21
Halbleiterbauelemente
Dotierung des Halbleiters
Man kann die Leitfähigkeit des Halbleiters gezielt durch den Einbau von
Fremdatomen ins Kristallgitter (sog. Störstellen) verändern, und zwar um
Größenordnungen. Für die Halbleitermaterialien Silizium und Germanium,
die 4 Valenzelektronen haben, werden zumeist folgende Elemente
verwendet:
Elemente mit 5 Valenzelektronen:
Arsen (As)
Antimon (Sb)
Phosphor (P)
Elemente mit 3 Valenzelektronen:
Bor (B)
Aluminium (Al)
Indium (In)
Der Einbau von Fremdatomen wird Dotieren (engl. doping) genannt.
Die Konzentrationen der Fremdatome (sog. Dotierungsgrad) liegt zwischen
1013 und 1020 Fremdatomen/cm3.
Folie 6-22
Halbleiterbauelemente
Dotierung mit 5-wertigen Elementen (n-Dotierung)
Beim Einbau von 5-wertigen Elementen (sog.
Donatoren) in das Kristallgitter gehen nur 4
Valenzelektronen eine kovalente Bindung ein. Das
fünfte Elektron ist nur lose an den Kern gebunden,
d.h. es kann mit geringem Energieaufwand ins
Leitungsband gehoben werden. Wenn das passiert,
bleibt im Gitter ein positiv geladener Atomrumpf
zurück.
Die Energieniveaus der Donatoren (ED) liegen nur
geringfügig (~ 0,05 eV) unter der Leitungsbandkante.
P+
T
0K
EC
ED
EC
ED
EC
ED
EV
EV
EV
steigende Temperatur
Störstellenreserve
Zimmertemperatur
Störstellenerschöpfung
Folie 6-23
Halbleiterbauelemente
Dotierung mit 3-wertigen Elementen (p-Dotierung)
Beim Einbau von 3-wertigen Elementen (sog.
Akzeptoren) in das Kristallgitter gehen 3 Valenzelektronen eine kovalente Bindung ein. Dem
Fremdatom fehlt ein weiteres Elektron für die
Bindung an alle Nachbaratome. Es "besitzt ein
Loch", in das unter geringem Energieaufwand
Nachbarelektronen springen können. Wenn das
passiert, stellt das Akzeptoratom eine ortsfeste
negative Ladung dar.
Die Energieniveaus der Akzeptoren (EA) liegen nur
geringfügig (~ 0,05 eV) über der Valenzbandkante.
B−
T
0K
EC
EC
EC
EA
EV
EA
EV
EA
EV
steigende Temperatur
Störstellenreserve
Zimmertemperatur
Störstellenerschöpfung
Folie 6-24
Halbleiterbauelemente
Störleitung
Bei Zimmertemperatur sind alle Störstellen (Akzeptoren oder Donatoren) ionisiert. Die
Leitfähigkeit ist im Wesentlichen durch die Dotierung festgelegt. Man spricht (im
Gegensatz zur Eigenleitung eines undotierten Halbleiters) von Störstellenleitung.
n
ND
2,0
In einem n-dotierten Halbleiter
herrscht dann ein Elektronenüberschuss. Es werden gleichzeitig
mehr Löcher durch Rekombination
aufgefüllt. Ihre Zahl geht dadurch
zurück. Im n-Halbleiter bezeichnet
man die Elektronen daher als
Majoritätsträger, die Löcher als
Minoritätsträger.
Störstellenreserve
1,5
Störstellenerschöpfung
1,0
0,5
Eigenleitung
100
200
300
400
500
600
T
K
Schematische Darstellung der Majoritätsträgerkonzentration für n-dotiertes Silizium.
(ND=1015 cm-3)
In einem p-dotierten Halbleiter sind
die Verhältnisse gerade umgekehrt.
Die Löcher sind die Majoritätsträger,
die Elektronen die Minoritätsträger.
Folie 6-25
Halbleiterbauelemente
pn-Übergang
Die Funktion der meisten Halbleiterbauelemente beruht darauf, dass im Halbleiter
Zonen unterschiedlicher Dotierung existieren.
Wir betrachten zunächst den Fall, dass ein p-dotierter und ein n-dotierter Halbleiter in
Kontakt gebracht werden. Wir nehmen an, dass alle Störstellen (Akzeptoren und
Donatoren) ionisiert sind.
Im p-Halbleiter sind die Löcher als
Majoritätsträger in großer Zahl
vorhanden, im n-Halbleiter
entsprechend die Elektronen. Aufgrund
des Konzentrationsunterschiedes
bewegen sich Löcher vom p-Halbleiter
p-Halbleiter
n-Halbleiter
in den n-Halbleiter und Elektronen vom
n-Halbleiter in den p-Halbleiter. Dort
sind sie jeweils Minoritätsträger.
Diese Ladungsträgerbewegung geschieht als thermische Diffusion.
Die Löcher, die im n-Halbleiter ankommen, rekombinieren dort mit Elektronen.
Die Elektronen, die im p-Halbleiter ankommen, rekombinieren dort mit Löchern.
Da die ionisierten Störstellenatome an ihre Orte im Kristallgitter gebunden sind,
entsteht eine Raumladungszone, in der so gut wie keine beweglichen Ladungsträger
vorhanden sind (Sperrschicht, Verarmungszone).
Folie 6-26
Halbleiterbauelemente
pn-Übergang im thermischen Gleichgewicht
Sperrschicht
pBahngebiet
nBahngebiet
p-Halbleiter
Raumladungsdichte
n-Halbleiter
(x)
x
elektrische Feldstärke
E(x)
elektrisches Potential
(x)
UD
x
Die Raumladungszone (x) erzeugt
ein elektrisches Feld E(x). Dieses
wirkt der thermischen Diffusion der
Ladungsträger entgegen. Es entsteht
ein Gleichgewicht, bei dem sich der
Diffusionsstrom und Driftstrom
(Strom aufgrund des elektrischen
Feldes) kompensieren.
Das elektrische Feld verursacht eine
Potentialdifferenz zwischen nHalbleiter und p-Halbleiter, die
sogenannte Diffusionsspannung
UD. Ihr Wert ist abhängig von der
Dotierung und liegt meistens bei
etwa 0,7 Volt.
x
Folie 6-27
Halbleiterbauelemente
pn-Übergang im Bändermodell (1)
Sperrschicht
pBahngebiet
Energie der Elektronen, E
p-Halbleiter
nBahngebiet
n-Halbleiter
eUD
EC
eUD
EV
x
Der Potentialunterschied (die Diffusionsspannung) sorgt für eine "Verbiegung" der Bänder. Elektronen im
p-Bahngebiet (dort Minoritätsträger)
besitzen nun eine potentielle Energie
gegenüber dem n-Bahngebiet. In der
Sperrschicht werden sie durch das
elektrische Feld in positiver x-Richtung beschleunigt. ("Sie rutschen die
Leitungsbandkante hinab.")
Für die Löcher im n-Bahngebiet (dort
ebenfalls Minoritätsträger) kann man
eine ähnliche Betrachtung anstellen.
Sie besitzen eine positive potentielle
Energie gegenüber dem p-Bahngebiet.
In der Sperrschicht werden sie durch
das elektrische Feld in negativer xRichtung beschleunigt. ("Sie steigen
wie Luftblasen an der Valenzbandkante empor.")
Folie 6-28
Halbleiterbauelemente
pn-Übergang im Bändermodell (2)
Sperrschicht
pBahngebiet
Energie der Elektronen, E
p-Halbleiter
Für die Majoritätsträger (Elektronen
im n-Bahngebiet und Löcher im pBahngebiet) ist es schwierig, auf die
jeweils andere Seite zu diffundieren.
Sie müssen mindestens die
thermische Energie eUD besitzen,
um die Potentialbarriere des
elektrischen Feldes der Sperrschicht
zu überwinden. Es fließt ein
geringer Diffusionsstrom.
nBahngebiet
n-Halbleiter
eUD
EC
eUD
EV
Im thermischen Gleichgewicht
halten sich beide Ströme die Waage,
d.h. die thermische Diffusion der
Majoritätsträger kompensiert den
Driftstrom der Minoritätsträger.
x
Folie 6-29
Halbleiterbauelemente
pn-Übergang: Anlegen einer Spannung – Sperrpolung
Sperrschicht
pBahngebiet
nBahngebiet
p-Halbleiter
−
elektrisches Potential
U+UD
UD
n-Halbleiter
U
+
(x)
x
Legen wir eine negative Spannung
zwischen p-Halbleiter und n-Halbleiter an (der p-Halbleiter wird an den
Minuspol angeschlossen, der n-Halbleiter an den Pluspol), dann werden
die freien Ladungsträger von den
Elektroden angezogen. Das elektrische Feld wird größer und die Raumladungszone wird breiter. Der pnÜbergang ist in Sperrrichtung
gepolt. Nur Minoritätsträger, die
durch thermische Generation entstehen, können zu einem Stromfluss
beitragen. Dieser Sperrstrom ist von
der Spannung unabhängig, jedoch
abhängig von der Temperatur. Er ist
sehr klein (im Bereich von µA).
Folie 6-30
Halbleiterbauelemente
pn-Übergang: Anlegen einer Spannung – Flusspolung
Sperrschicht
pBahngebiet
nBahngebiet
p-Halbleiter
+
elektrisches Potential
UD
U−UD
n-Halbleiter
U
−
(x)
x
Legen wir eine positive Spannung
zwischen p-Halbleiter und n-Halbleiter an (der p-Halbleiter wird an
den Pluspol angeschlossen, der nHalbleiter an den Minuspol), dann
verringert sich das elektrische Feld
und die Raumladungszone wird
schmaler. Man sagt, der pn-Übergang ist in Flussrichtung oder
Durchlassrichtung gepolt.
Die Ladungsträger können nun mit
wesentlich geringerem Energieaufwand den Übergang passieren.
Der Diffusionsstrom vom p- ins nGebiet überwiegt den entgegengerichteten Driftstrom. Es fließt ein
positiver "Nettostrom".
Folie 6-31
Halbleiterbauelemente
Diode
Schaltsymbol der Diode
Der pn-Übergang lässt Stromfluss nur in
Durchlasspolung zu. (In Sperrrichtung
fließt lediglich der vernachlässigbar
kleine Sperrstrom, im Bereich von µA).
Ein pn-Übergang stellt eine Diode dar.
Die Kennlinie der idealen Diode ergibt
sich aus der Kennliniengleichung
I
I = I S ( eU / U T −1)
U
UT : sog. Temperaturspannung.
UT ≈ 25.2 mV bei Raumtemperatur.
IS : Sättigungsstrom in Sperrrichtung.
US
I
I
R=
US
Modell mit
Schleusenspannung
U
US
ΔU
ΔI
U
Modell mit
Schleusenspannung
und Bahnwiderstand
In vielen Fällen kann eine reale
Diodenkennlinie durch zwei
Geradenstücke angenähert werden.
Dabei ist der Schnittpunkt der Tangente
an die Kurve die sogenannte
Schleusenspannung US.
US ≈ 0,7 V bei Si, bei Raumtemperatur.
Folie 6-32
Halbleiterbauelemente
Bipolartransistor
Der Transistor wurde 1947 in den Bell Laboratories von Shockley, Bardeen und
Brattain erfunden. Er heißt Bipolartransistor, weil in ihm beide Ladungsträgertypen
(Elektronen und Löcher) zum Stromtransport beitragen.
Der Transistor besteht aus drei Zonen unterschiedlich dotierten Halbleitermaterials.
Beim npn-Transistor werden zwei n-dotierte Gebiete durch ein p-dotiertes Gebiet
getrennt. Beim pnp-Transistor werden zwei p-dotierte durch ein n-dotiertes Gebiet
getrennt. Es ergibt sich jeweils eine Abfolge von zwei nebeneinanderliegenden pnÜbergängen.
Die Zonen haben die Bezeichnungen Emitter (E), Basis (B) und Kollektor (C).
C
C
C
p
n
B
p
C
B
B
n
B
p
n
E
E
npn-Transistor
E
E
pnp-Transistor
Folie 6-33
Halbleiterbauelemente
(Bipolartransistor)
Die pn-Übergänge stellen Halbleiterdioden dar. Man spricht von der Basis-EmitterDiode (BE-Diode) und der Basis-Kollektor-Diode (BC-Diode).
Im Normalbetrieb wird die BE-Diode in Durchlassrichtung, die BC-Diode in
Sperrrichtung gepolt.
Beim npn-Transistor werden in dieser
Beschaltung Elektronen vom Emitter in
IC
das Basisgebiet injiziert. Die
UCB > 0
IB
Elektronen, die in der Basis nicht mit
UCE > 0
Löchern rekombinieren, können in die
Sperrschicht der BC-Diode
UBE > 0
IE
diffundieren. Dort werden sie durch
das elektrische Feld "abgesaugt" und
zum Kollektor transportiert.
Damit die injizierten Elektronen den Kollektor erreichen können, bevor sie mit Löchern
in der Basis rekombinieren, wird die Basisweite sehr klein gewählt.
Die Basis injiziert ihrerseits Löcher in den Emitter, die dort mit Elektronen
rekombinieren. Durch eine entsprechend schwache Dotierung der Basis sorgt man
dafür, dass der Basisstrom IB viel kleiner ist als der Emitterstrom IE.
Folie 6-34
Halbleiterbauelemente
Ströme (npn-Transistor)
n
p
n
IE
IC
E
C
IB
Stromanteile im npn-Transistor
bei Normalbetrieb:
•
•
B
Elektronen als Emitterstrom IE aus dem Emitterbereich in die Basis. Der größte
Teil gelangt als Transferstrom zum Kollektor und bildet den Kollektorstrom IC.
Ein kleiner Teil rekombiniert mit Löchern in der Basis.
Löcher als Löcherstrom aus dem Basisbereich in den Emitter. Zusammen mit
den in der Basis rekombinierenden Elektronen bildet er den Basisstrom IB.
Folie 6-35
Halbleiterbauelemente
Stromverstärkung (npn-Transistor)
Mit der an der BE-Diode anliegenden Spannung in Durchlassrichtung kann die Rate der
vom Emitter in die Basis injizierten Elektronen und damit auch die Rate der am
Kollektor ankommenden Elektronen gesteuert werden. Der Kollektorstrom IC wird also
durch die Spannung UBE gesteuert. Die Basis wirkt dabei als Steuerelektrode.
Da der gesteuerte Kollektorstrom wesentlich größer ist als der Basisstrom, stellt der
Bipolartransistor ein Halbleiterbauelement mit Verstärkereigenschaften dar. Das
Verhältnis von Kollektorstrom zu Basisstrom im Normalbetrieb wird bezeichnet
als
IC
Der Wert von BN liegt typischerweise
Stromverstärkung
BN =
zwischen 100 und 200, ist also sehr
IB
viel größer als 1.
Integrierter npn-Transistor
Weil der Transistor (nur!) im Prinzip
symmetrisch aufgebaut ist, kann man
die Anschlüsse von Kollektor und
Emitter vertauschen. In einem solchen
Rückwärtsbetrieb (Inversbetrieb) ist die
Stromverstärkung allerdings viel
kleiner (≈1).
Folie 6-36
Halbleiterbauelemente
Kennlinien des Bipolartransistors (Beispiel)
IB
IB = 100 µA
IC
100 µA
10 mA
IB = 80 µA
80 µA
8 mA
IB = 60 µA
60 µA
6 mA
IB= 40 µA
40 µA
4 mA
IB= 20 µA
20 µA
2 mA
IB= 0 µA
0
0,2V
0,4V 0,6V
0,8V UBE
0
Eingangskennlinie
5V
10V
Ausgangskennlinien
Beispiel: Kennlinien für einen npn-Transistor
Folie 6-37
UCE
Halbleiterbauelemente
Betriebsbereiche des npn-Transistors
Gesperrter Bereich:
Beide pn-Übergänge sind gesperrt (UBE < US; –UCB < US; US: Schleusenspannung).
Über den Transistor fließen trotz angelegter Ausgangsspannung UCE > 0 nur sehr kleine
Restströme. Der Transistor hat einen hohen Kollektor-Emitter-Widerstand – er entspricht einem geöffneten Schalter. (Im Kennlinienfeld der vorigen Folie: Kennlinie für
IB=0µA).
Linearer Bereich:
Der Basis-Emitter-Übergang ist leitend, der Basis-Kollektor-Übergang ist gesperrt
(UBE > US; –UCB < US). Die Injektion von Elektronen in die Basis wird durch die BasisEmitter-Spannung gesteuert, der Kollektorstrom IC hängt kaum von UCE ab. (Dieser
Bereich wird in der Verstärkertechnik verwendet).
Gesättigter Bereich:
Beide pn-Übergänge sind leitend (UBE > US; –UCB > US). Dies wird erreicht, wenn die
Kollektor-Emitter-Spannung UCE kleiner als die Basis-Emitter-Spannung UBE gewählt
wird. Dann injizieren sowohl Emitter als auch Kollektor Elektronen in die Basis –
Kollektor- und Basisstrom steigen stark an. Dies entspricht einem niedrigen Widerstand
– in der Digitaltechnik verwendet man den Transistor in diesen Zustand wie einen
geschlossenen Schalter.
Folie 6-38
Halbleiterbauelemente
Bipolartransistor als gesteuerter Schalter
Durch Änderung der Basis-Emitter-Spannung UBE kann der Strom IC gesteuert
werden. Damit eignet sich der Bipolartransistor als gesteuerter Schalter.
IC
IB, EIN > 0
Für die Anwendung als Schalter kommen
zwei Arbeitspunkte in Frage:
1.
Arbeitspunkt "EIN": Bei Ansteuerung
mit einer hohen Basis-Emitter-Spannung
fällt auch bei hohem Strom IC nur eine
geringe Kollektor-Emitter-Spannung ab.
Der Transistor hat einen niedrigen
Kollektor-Emitter-Widerstand.
2.
Arbeitspunkt "AUS": Bei Ansteuerung
mit einer kleinen Basis-EmitterSpannung fließt so gut wie kein Strom IC.
Der Transistor hat einen hohen
Kollektor-Emitter-Widerstand.
Arbeitspunkt "EIN":
Hoher Strom bei niedriger
Spannung
niedriger Widerstand
Arbeitspunkt "AUS":
Niedriger Strom bei hoher
Spannung
hoher Widerstand
IB, AUS = 0
0
UCE
Folie 6-39
Halbleiterbauelemente
Isolierschicht-Feldeffekttransistor (MOSFET)
MOSFETs sind die wichtigsten Bauelemente heutiger integrierter Digitalschaltungen.
MOS steht für Metall-Oxid-Silizium-Kapazität. FET steht für Feld-Effekt-Transistor.
Es gibt n-Kanal- und p-Kanal-MOSFETs.
Wesentlicher Bestandteil des MOSFETs ist der MOS-Kondensator. Er besteht aus der
Gate-Elektrode ("Metall"), dem Dielektrikum aus Siliziumdioxid ("Oxid") und dem
Substrat ("Silizium"). Das Substrat ist mit dem Anschluss "Bulk" verbunden.
Gate (G)
Isolierschicht
SiO2
Source
(S)
schematischer Aufbau
Substrat
p-Silizium
Drain
(D)
Bulk
Folie 6-40
Halbleiterbauelemente
MOS-Kapazität
G
UGB > 0
UGB < Uth
p-Si
B
Verhalten der MOS-Kapazität eines
n-Kanal-MOSFET:
Bei Anlegen einer positiven
Spannung UGB zwischen Gate und
Bulk bildet sich im n-KanalMOSFET an der Grenzfläche
zwischen Substrat und Oxid eine
negative Influenzladung. Sofern die
Spannung nicht zu groß ist, besteht
diese Influenzladung lediglich aus
einer negativen Raumladungszone
(Verarmungszone, Sperrschicht).
Verhalten der MOS-Kapazität eines p-Kanal-MOSFET:
Sie verhält sich prinzipiell wie die des n-Kanal-MOSFET, allerdings sind die
Polaritäten der Spannungen und Ladungen umzukehren.
Im Folgenden betrachten wir die Verhältnisse beim n-Kanal-MOSFET. Die
Bedingungen für den p-Kanal-MOSFET können daraus leicht abgeleitet werden.
Folie 6-41
Halbleiterbauelemente
(MOS-Kapazität)
G
UGB > Uth
p-Si
B
(Verhalten der MOS-Kapazität eines
n-Kanal-MOSFET: )
Überschreitet die Spannung UGB die sogenannte Schwellspannung Uth, (engl.
threshold voltage) dann kann die Gate-Ladung nicht mehr alleine durch die
Raumladung im p-Silizium kompensiert werden. Es bildet sich eine dünne Schicht
freier Elektronen (entstanden aus thermischer Generation), genannt Kanal. An der
Oberfläche des p-Siliziums hat eine Umkehr (Inversion) des Leitungstyps
stattgefunden. Der Kanal ist n-leitend geworden (Inversionskanal). Es existieren
nun freie Ladungsträger, die für Stromtransport zur Verfügung stehen.
Folie 6-42
Halbleiterbauelemente
Schwellspannung Uth
Die Schwellspannung Uth ist abhängig von der Geometrie der Anordnung, der Substratdotierung, dem Gatematerial sowie von festen Flächenladungen an der Si-SiO2-Grenzfläche. Sie lässt sich bei der Herstellung in gewissen Grenzen einstellen. Sie kann sogar
negativ werden: Wird unterhalb der Isolierschicht ein leitender Kanal eingebracht (z.B.
durch Ionenimplantation), dann fließt bereits bei UGS= 0 ein Strom, wenn an den Kanal
eine Spannung UDS angelegt wird. Eine negative Schwellspannung Uth bedeutet also:
Erst wenn die Gate-Source-Spannung negativ ist und unterhalb von Uth liegt, wird ein
solcher Transistor ausgeschaltet. Ansonsten leitet er.
n-Kanal-MOSFETs werden nach dem Vorzeichen ihrer Schwellspannung klassifiziert
in zwei Typen:
Uth > 0:
selbstsperrend, "Anreicherungstyp", engl. "enhancement mode"
Uth < 0:
selbstleitend, "Verarmungstyp", engl. "depletion mode"
Für p-Kanal-MOSFETs gilt Entsprechendes. Es ändern sich nur die Vorzeichen aller
Spannungen und Ströme.
Folie 6-43
Halbleiterbauelemente
Integrierter n-Kanal-MOSFET
Source (S)
Gate (G)
UGS > Uth
Drain (D)
SiO2
n
D
Raumladungszone
G
n
S
p-Substrat
n-Kanal
Schaltsymbol
n-Kanal-MOSFET
L
Ein integrierter n-Kanal-MOSFET besteht aus einem p-Substrat mit zwei stark ndotierten Zonen im Abstand L (Kanallänge) voneinander. Die n-Zonen bilden Source
und Drain des Transistors. Über dem Kanalgebiet befindet sich die Isolierschicht (SiO2)
und darüber die Gate-Elektrode. Der Bulk-Anschluss ist meist mit dem niedrigsten
Potential in der gesamten Schaltung (z.B. 0V, Masse) verbunden.
Legt man eine positive Gate-Source-Spannung UGS > Uth an, so bildet sich die
Raumladungszone und der n-leitende Kanal aus.
Legt man dann eine positive Drain-Source-Spannung UDS an, so fließt ein Strom. Der
MOSFET verhält sich dann wie ein spannungsgesteuerter Widerstand.
Folie 6-44
Halbleiterbauelemente
Integrierter p-Kanal-MOSFET
Source (S)
Gate (G)
Drain (D)
D
UGS < Uth
SiO2
p
Raumladungszone
G
p
n-Substrat
UB
p-Kanal
S
Schaltsymbol
p-Kanal-MOSFET
Der p-Kanal-MOSFET ist entsprechend aus n-Substrat und p-dotierten Zonen für
Source und Drain aufgebaut. Der Bulk-Anschluss ist meist mit dem höchsten
Potential in der gesamten Schaltung verbunden (z.B. Betriebsspannung UB).
Um die Inversion einzuleiten, ist eine negative Gate-Source-Spannung UGS < Uth
notwendig. Eine negative Drain-Source-Spannung UDS führt zu einem Stromfluss
durch den Transistor.
Folie 6-45
Halbleiterbauelemente
Abschnüreffekt (pinch-off) beim n-Kanal-MOSFET
UGS > Uth
UDS > UGS−Uth
G
S
n
D
Raumladungszone
n
p
Kanal
"pinch-off"
Mit zunehmender Spannung wird die influenzierte Ladung im Kanal ortsabhängig.
Durch den Spannungsabfall im Kanal wird am Kanalende kaum noch Ladung
influenziert. Der Kanal wird "abgeschnürt" (engl.: "pinched off"). Dies führt dazu,
dass der Strom ID nicht mehr weiter ansteigen kann, sondern einen Sättigungswert
annimmt. Dieser hängt von der Gate-Source-Spannung UGS ab.
Folie 6-46
Halbleiterbauelemente
Betriebsbereiche des n-Kanal-MOSFET
Sperrbereich:
UGS < Uth
ID
ID = 0
UDS
Der Transistor sperrt, es fließt kein nennenswerter
Drainstrom. Das Kanalgebiet hat einen sehr hohen
Widerstand.
UGS
Widerstandsbereich oder ohm'scher Bereich:
UGS > Uth
UDS < UGS − Uth = UDS,sat
U DS ⎞
⎛
I D = β ⎜U GS − U th −
⎟U DS
2 ⎠
⎝
mit
β = μe
ε 0ε r W
tox L
Der Faktor enthält Geometriegrößen (Kanalbreite W, Kanallänge L, Dicke
des Gateoxids tox) sowie Materialgrößen (Beweglichkeit µe der Elektronen,
Dielektrizitätszahl r des Gateoxids).
Der Transistor verhält sich wie ein spannungsgesteuerter Widerstand. Sein
Leitwert ändert sich in Abhängigkeit von UGS.
Folie 6-47
Halbleiterbauelemente
(Betriebsbereiche des n-Kanal-MOSFET)
ID
Sättigungsbereich oder Abschnürbereich:
UGS > Uth
UDS
UDS ≥ UGS − Uth = UDS,sat
UGS
I D,sat =
β
2
(U GS − U th )2
mit
β = μe
ε 0ε r W
tox L
Der Drainstrom ändert sich nicht mehr bei weiterer Erhöhung der DrainSource-Spannung UDS über den Wert UDS,sat= UGS − Uth hinaus.
Betriebsbereiche des p-Kanal-MOSFET
Für die Betriebsbereiche des p-Kanal-MOSFET gilt Entsprechendes; es
sind dabei lediglich die Vorzeichen der Spannungen und Ströme sowie die
Vergleichsoperatoren (<, ≤, >, ≥) umzukehren.
Folie 6-48
Halbleiterbauelemente
Kennlinien des MOSFET (Beispiel)
WiderstandsBereich
ID
ID
0,8 mA
UGS= 3,0 V
0,8 mA
Sättigungsbereich
UGS= 2,6 V
UDS=6 V
0,6 mA
0,6 mA
0,4 mA
0,4 mA
UGS= 2,2 V
0,2 mA
0,2 mA
Uth= 1 V
Sperrbereich UGS= 1,8 V > Uth
UGS= 0,5 V < Uth
0
1V
2V
3 V UGS
Transferkennlinie
0
4V
2V
6V
8V
Ausgangskennlinien
Beispiel: Kennlinien für einen n-Kanal-MOSFET
Folie 6-49
UDS
Halbleiterbauelemente
MOSFET als gesteuerter Schalter
Durch Änderung der Gate-Source-Spannung UGS kann der Strom ID gesteuert werden.
Damit eignet sich auch der MOSFET als gesteuerter Schalter.
ID
Für die Anwendung als Schalter kommen
zwei Arbeitspunkte in Frage:
UGS, EIN > Uth
1.
Arbeitspunkt "EIN": Bei Ansteuerung
mit einer Spannung UGS > Uth ist der
Transistor leitend, d.h. bei hohem
Drainstrom fällt eine geringe DrainSource-Spannung ab. Der Transistor hat
einen niedrigen Drain-SourceWiderstand.
2.
Arbeitspunkt "AUS": Bei Ansteuerung
mit einer Spannung UGS < Uth sperrt der
Transistor. Es fließt so gut wie kein ID.
Der Transistor hat einen hohen DrainSource-Widerstand.
Arbeitspunkt "EIN":
Hoher Strom bei niedriger
Spannung
niedriger Widerstand
Arbeitspunkt "AUS":
Niedriger Strom bei hoher
Spannung
hoher Widerstand
UGS, AUS < Uth
0
UDS
Folie 6-50
Halbleiterbauelemente
Schaltkreisfamilien
Schaltkreisfamilien sind Kollektionen standardisierter digitaler Bausteine, die die
gleiche Basistechnologie verwenden und gleiche elektronische Kenngrößen besitzen.
Man kann aus ihnen auf einfache Weise größere Digitalschaltungen zusammensetzen.
In den frühen Jahren der Mikroelektronik wurden integrierte Digitalschaltungen
zunächst mit Bipolartransistoren aufgebaut. Die ersten Schaltkreisfamilien hießen
RTL (Resistor-Transistor Logic), DTL (Diode-Transistor Logic), TTL (TransistorTransistor Logic) und ECL (Emitter-Coupled Logic). TTL und ECL werden auch
heute noch in bestimmten Anwendungen eingesetzt.
Der Großteil der integrierten Digitalschaltungen, aus denen informationstechnische
Systeme heute aufgebaut werden, basieren auf der MOS-Technik. Hier hat sich
insbesondere die CMOS-Technologie durchgesetzt (CMOS=Complementary MOS).
Dazu mehr im nächsten Kapitel.
Folie 6-51
Halbleiterbauelemente
Vergleich Bipolartechnologie vs. MOS-Technologie
Vorteile der Bipolartechnologie:
•
•
•
Fähigkeit, große Ströme zu treiben (dadurch sind schnelle Umladevorgänge
möglich).
Die Basis-Emitter-Schleusenspannung von ca. 0,7 V ist sehr stabil und
reproduzierbar einzustellen und nur wenig von der Prozesstechnologie abhängig.
Kurze Umschaltzeiten und damit hohe Arbeitsfrequenzen möglich.
Vorteile der MOS-Technologie:
•
•
•
Weil das Gate isoliert ist, fließt im stationären Fall kein Strom ins Gate. Dadurch
niedrige Leistungsaufnahme.
Der stromführende Kanal ist durch den Transistoraufbau bereits isoliert. Dadurch
ist keine zusätzliche Isolation notwendig. Ein MOS-Transistor ist ein sehr
platzsparendes Bauelement und erlaubt daher hohe Integrationsdichten.
Schwellspannung Uth ist einstellbar.
Die Weiterentwicklung der Technologie führt allerdings auch bei der MOS-Technik
zu immer schnelleren Bauelementen, so dass der Geschwindigkeitsvorsprung der
Bipolartechnik allmählich verschwindet.
Folie 6-52
Technische Informatik I
Kapitel 7
Digitale Grundschaltungen
Folie 7-1
Digitale Grundschaltungen
Informationsverarbeitung in digitalen Schaltungen
Die technische Informationsverarbeitung beruht auf der Kodierung der
Information durch zwei Werte (binäre Kodierung). Die Information wird
dabei durch physikalische Größen wie z.B. Strom oder Spannung
repräsentiert. Die Prozesse der räumlichen und zeitlichen Änderung dieser
physikalischen Größen beschreiben wir mathematisch durch Signale. Man
benötigt eine eindeutige Zuordnung der beiden binären Informationswerte zu
den Werten der Signale. Man spricht von Signalpegeln, denen die
Informationswerte zugeordnet sind.
In den herkömmlichen Schaltkreisfamilien (TTL, CMOS) wird die
Information in den Werten der elektrischen Spannung kodiert. Man
identifiziert einen hohen Spannungspegel, genannt Hi, und einen niedrigen
Spannungspegel, genannt Lo, mit den logischen Werten 0 oder false und 1
oder true. Es gibt zwei Möglichkeiten der Zuordnung:
positive Logik:
negative Logik:
0 (false) Lo, 1 (true) Hi
0 (false) Hi, 1 (true) Lo
Im Folgenden verwenden wir in unseren Beispielen positive Logik.
Folie 7-2
Digitale Grundschaltungen
Implementierung digitaler Systeme mit gesteuerten Schaltern
In vielen Bausteinfamilien der 1970er und 1980er Jahre betrug der Hi-Wert
des Spannungspegels 5V. Für heutige hochintegrierte Transistoren, die viel
geringere Bauelementeabmessungen haben (das Gateoxid z.B. ist nur noch
wenige Atomlagen dick), wären diese Spannungen zu hoch. Mit der
fortschreitenden Miniaturisierung der geometrischen Abmessungen werden
auch die Betriebsspannungen (und damit der Hi-Pegel) kleiner. Typische
Werte sind heutzutage 3V, 1.8V, 1.5V oder darunter.
Mit dem Bipolartransistor und dem MOSFET stehen uns steuerbare Schalter
zur Verfügung. Das einfachste Modell dieser Bauelemente in positiver Logik
sieht demnach so aus:
Bipolartransistor:
C
B = Lo
B = Hi
C
C
OFF
B
E
E
ON
E
Folie 7-3
Digitale Grundschaltungen
Implementierung digitaler Systeme mit gesteuerten Schaltern
MOSFET:
D
G = Lo
G = Hi
D
D
G
nMOS
OFF
S
S
S
D
D
D
ON
G
pMOS
ON
S
S
OFF
S
Folie 7-4
Digitale Grundschaltungen
Implementierung digitaler Systeme mit gesteuerten Schaltern
gesteuerter Schalter
Ein gesteuerter Schalter verbindet zwei Punkte in
Abhängigkeit von einem Steuersignal.
Normally Open
wenn das Steuersignal 0 (false) ist, ist der Schalter offen
wenn das Steuersignal 1 (true) ist, ist der Schalter geschlossen
Normally Closed
wenn das Steuersignal 0 (false) ist, ist der Schalter geschlossen
wenn das Steuersignal 1 (true) ist, ist der Schalter offen
True
Steuersignal
geschlossener
Schalter
True
Steuersignal
False
offener
Schalter
False
Normally Closed
Normally Open
offener
Schalter
geschlossener
Schalter
Folie 7-5
Digitale Grundschaltungen
Netzwerke von Schaltern
Beispiel:
WENN Ampel für Hauptstraße grün
UND Ampel für einmündende
Straße rot
True
UND 45 s seit letztem Wechsel
DANN Ampel für Hauptstraße
wird gelb
Beispiel:
WENN 45 s seit letztem Wechsel
ODER (Fußgänger drückt
UND NICHT weniger als 10s
seit letztem Wechsel)
Hauptstraße grün
UND
DANN Hauptstraße wird gelb
Hauptstraße
grün
einmündende
Straße rot
45 s seit
letztem Wechsel
Hauptstraßenampel
wird gelb
weniger als 10 s
seit Wechsel
Fußgänger
drückt
Hauptstraße
grün
True
Hauptstraßenampel wird gelb
True
45 s seit
letztem Wechsel
Knoten im Schwebezustand (floating):
was passiert, wenn Hauptstraße nicht grün?
Ausgang im Schwebezustand und nicht auf False
Wichtige Prinzipien in einem Schalternetzwerks: Für alle Werte der Steuersignale gilt:
(1) alle Ausgänge müssen über irgendeinen Pfad entweder mit True oder
mit False verbunden sein (kein Schwebezustand)
(2) kein Ausgang ist gleichzeitig mit True und False verbunden (keine Konflikte)
Folie 7-6
Digitale Grundschaltungen
Implementierung von AND- und OR-Funktion durch Schalter
A
False
B
A
output
True
AND-Operation
(Konjunktion)
Serienschaltung zu TRUE
B
False
output
True
OR-Operation
(Disjunktion)
Parallelschaltung zu TRUE
Folie 7-7
Digitale Grundschaltungen
Schaltlogik
Ein Netzwerk aus normally open- und normally closed-Schaltern, das für jede
binäre Wertekombination an den Steuersignalen einen binären Signalwert true
oder false auf den Ausgang durchschaltet, kann durch eine aussagenlogische
Formel beschrieben werden.
Die Wertekombination an den Steuersignalen entspricht der Belegung der
Formel. Der binäre Signalwert am Ausgang des Netzwerks entspricht dem
Wahrheitswert der Formel.
Schreibweisen in der Digitaltechnik:
a + b statt a ∨ b
a · b oder ab statt a ∧ b
a' oder a statt ¬a
a = 1 statt A(a) = 1
f = g statt f ≡ g
f ⊕ g statt f ↔ g
Schalternetzwerke, die
grundlegende logische
Operationen (UND, ODER,
NICHT …) realisieren, werden zu
„Gattern“ zusammengefasst. Sie
dienen als Bauelemente einer
digitalen Schaltung.
Folie 7-8
Digitale Grundschaltungen
Logische Gatter und Schaltlogik
Gattersymbol
x
NOT (Negation)
AND (Konjunktion)
OR (Disjunktion)
x
y
x
y
Wahrheitstabelle
x
0
1
x
z
z
x
0
0
1
1
x
0
0
1
1
x
1
0
y
0
1
0
1
z
0
0
0
1
y
0
1
0
1
z
0
1
1
1
Schalternetzwerk
true
x
false
x
false
x·y
true
x
y
false
x +y
true
x
Folie 7-9
y
Digitale Grundschaltungen
NAND, NOR
Wahrheitstabelle
Gatter
NAND
x
y
z
x
0
0
1
1
y
0
1
0
1
z
1
1
1
0
Schalternetzwerk
true
x ·y
false
x
NOR
x
y
z
x
0
0
1
1
y
0
1
0
1
z
1
0
0
0
y
true
x +y
false
x
In der Praxis:
y
NAND- und NOR-Gatter kommen in der Praxis häufiger vor als
AND und OR.
technologisch einfacher realisierbar!
Auch NOT-Gatter (Inverter) können durch NAND oder NOR realisiert werden.
(NOT ist NAND oder NOR mit zusammengeschlossenen Eingängen)
Folie 7-10
Digitale Grundschaltungen
XOR, XNOR
XOR: x oder y aber nicht beides („Antivalenz“, „exclusive OR“)
XNOR: x und y sind gleich („Äquivalenz“)
XNOR-Gatter
XOR-Gatter
x
y
Wahrheitstabelle
x y
0 0
0 1
1 0
1 1
x ⊕ y = x y' + x' y
z
z
0
1
1
0
x
y
Wahrheitstabelle
x y
0 0
0 1
1 0
1 1
z
z
1
0
0
1
(x ⊕ y)' = x y + x' y'
Folie 7-11
Digitale Grundschaltungen
Gattersymbole
übliches Symbol
(amerikanisch)
nach DIN 40900
a
b
y
OR
a
b
≥1
y
a
b
y
AND
a
b
&
y
a
1
XOR
a
b
=1
NAND
a
b
&
y
y
NOR
a
b
≥1
y
y
XNOR
a
b
=1
y
a
a
b
a
b
a
b
a
b
y
Inverter (NOT)
y
y
y
y
Folie 7-12
Digitale Grundschaltungen
Logische Grundschaltungen mit gesteuerten Schaltern
Inverterschaltung mit Lastwiderstand
UB
UB
RL
RL
Steuersignal
Lo
Steuersignal
Ua = UB = Hi
Hi
Ua = 0V = Lo
Folie 7-13
Digitale Grundschaltungen
Inverter mit Bipolartransistor
UB
UB
RL
RL
IC
IC
Ua
Ue
Ua,2
Ue,2
Der Ausgang eines Gatters muss in der Lage sein, ein gleichartiges Gatter
korrekt anzusteuern. Das bedeutet, dass die Ausgangsspannung Ua gültige
Hi- und Lo-Spannungspegel erzeugen muss.
Folie 7-14
Digitale Grundschaltungen
Inverter mit Bipolartransistor
IC
UB
UB
RL
RL
ON
IC
Ua
Ue
OFF
Inverterschaltung
mit bipolarem Transistor
0
UB UCE =Ua
Kennlinienfeld des Bipolartransistors
mit Lastgeraden für RL
Folie 7-15
Digitale Grundschaltungen
(Inverter mit Bipolartransistor)
Arbeitspunkt "OFF":
Liegt an den Eingangsklemmen des Inverters ein Lo-Pegel
(d.h. für Ue = UBE < US ≈ 0,7V), so sperrt der Transistor. Es fließt ein
vernachlässigbar kleiner Kollektorstrom. Am Lastwiderstand RL fällt keine
nennenswerte Spannung ab. An den Ausgangsklemmen stellt sich der hohe
Spannungspegel Hi ein (im Sperrbereich des Kennlinienfeldes).
Arbeitspunkt "ON":
Liegt an den Eingangsklemmen des Inverters ein Hi-Pegel
(d.h. für Ue = UBE > 0,7V), so leitet der Transistor. Der Lastwiderstand
begrenzt dabei den Strom. (Würde der Transistor ideal leiten, so wäre der
Strom IC=UB/RL.) Der Transistor befindet sich im gesättigten Bereich (die
Basis-Kollektor-Diode ist in Flussrichtung gepolt). Es fällt die
Sättigungsspannung UCE,sat über dem Transistor ab. Diese Spannung ist
kleiner als die Schleusenspannung US und entspricht damit einem Lo-Pegel.
Ein an die Ausgangsklemmen angeschlossener Bipolartransistor (z.B. der
eines nachfolgenden Gatters) würde also sperren.
Folie 7-16
Digitale Grundschaltungen
Inverter in nMOS-Technik
UB
UB
nMOSLasttransistor
nMOSLasttransistor
ID
nMOSSchalttransistor
ID
Ua
Ue
nMOSSchalttransistor
CG
Ua,2
Ue,2
Inverter in nMOS-Technik
nachgeschalteter zweiter Inverter
Die Ausgangsspannung des ersten Inverters muss zwar keinen stationären
Strom an das nachgeschaltete Gatter liefern. Sie muss allerdings die GateKapazität CG des Eingangstransistors aufladen. Diese Kapazität wird
durch den eingezeichneten Kondensator modelliert.
Folie 7-17
Digitale Grundschaltungen
Inverter in nMOS-Technik
UB
ID
nMOSLasttransistor
ID
nMOSSchalttransistor
ON
Ua
UGS–Uth
Ue
OFF
0
Inverterschaltung
in statischer nMOS-Technik
mit Lasttransistor
UB–Uth
UB UDS =Ua
Kennlinienfeld des nMOSFET mit
Lastkennlinie des Lasttransistors
Folie 7-18
Digitale Grundschaltungen
(Inverter in nMOS-Technik)
Arbeitspunkt "OFF":
Liegt an den Eingangsklemmen des Inverters ein Lo-Pegel
(d.h. für Ue = UGS < Uth), so sperrt der Schalttransistor. Der Lasttransistor
lädt die nachfolgende Eingangskapazität CG. Dabei steigt die Ausgangsspannung an, allerdings nicht bis UB sondern nur bis UB–Uth, denn der
Lasttransistor sperrt ebenfalls, sobald seine Gate-Source-Spannung unter die
Schwellspannung fällt. Der Drainstrom des Schalttransistors ID ist 0. Der
Endwert der Ausgangsspannung Ue = UB–Uth ist ein Hi-Pegel.
Arbeitspunkt "ON":
Liegt an den Eingangsklemmen des Inverters ein Hi-Pegel
(d.h. für Ue = UGS > Uth), so leitet der Schalttransistor. Der Lasttransistor
leitet ebenfalls. Über die Wahl der Kanallängen L und Kanalbreiten W der
beiden Transistoren können ihre Widerstände eingestellt werden. Der Lasttransistor muss einen hohen, der Schalttransistor einen niedrigen Widerstand
besitzen, so dass im Arbeitspunkt "ON" die Ausgangsspannung Ua kleiner
ist als die Schwellspannung Uth des Eingangstransistors des nachfolgenden
Gatters. Diese Ausgangsspannung stellt einen Lo-Pegel dar.
Folie 7-19
Digitale Grundschaltungen
Inverter in CMOS-Technik
+5V
Hi
+5V
Lo
Eingang ist Hi
Lasttransistor sperrt
Schalttransistor leitet
Ausgang mit Lo verbunden
Lo
Hi
Eingang ist Lo
Lasttransistor leitet
Schalttransistor sperrt
Ausgang mit Hi verbunden
Folie 7-20
Digitale Grundschaltungen
Übertragungskennlinie eines CMOS-Inverters
Eingangsspannung Lo
Ua
5V
Inverterausgangsspannung Ua ist Funktion
der Eingangsspannung Ue
Eingangsspannung steigt von 0V auf 5V:
Ausgang behält 5V für einen gewissen
Bereich von Eingangsspannungswerten
bei, danach sinkt die Ausgangsspannung
schnell ab.
4V
3V
2V
1V
Ein wesentlicher Strom fließt nur beim
Umschalten, im undefinierten Spannungspegelbereich.
ID
0
1V
2V
3V
4V
5V Ue
Eingangsspannung Hi
Ein Logikgatter ist zunächst einmal eine elektronische Schaltung, die mit
analogen Strömen und Spannungen arbeitet.
Die Aussagenlogik beschreibt das Verhalten digitaler Systeme
im eingeschwungenen (stationären) Zustand.
Folie 7-21
Digitale Grundschaltungen
Zeitverhalten logischer Gatter (1)
Ue
t
Ua
t
Antwort eines Inverters auf einen Rechteckimpuls
Folie 7-22
Digitale Grundschaltungen
Zeitverhalten logischer Gatter (2)
Die zeitliche Verzögerung bei der
Berechnung logischer Funktionen
durch digitale Gatterschaltungen
wird im allgemeinen durch eine
summarische Größe namens
Gatterlaufzeit modelliert.
Ue
50%
t
Ua
50%
t
tpdL
tpdH
tpdL : propagation delay (Lo)
Gatterlaufzeit
(propagation delay):
tpdH : propagation delay (Hi)
tpd = ½ (tpdL+tpdH)
Folie 7-23
Digitale Grundschaltungen
CMOS-Transistorschaltungen für logische Gatter
pull-up-Netzwerk
a
+5V
b
+5V
a
+5V
Inverter
b
ab
a
GND
a
a+b
GND
GND
NAND-Gatter
NOR-Gatter
pull-down-Netzwerk
Folie 7-24
Digitale Grundschaltungen
Funktionsweise eines CMOS-NAND-Gatters
"1"
"0"
"1"
+5V
"1"
+5V
"0"
a = 1, b = 1
Pull-up-Netzwerk sperrt
Pull-down-Netzwerk leitet
Ausgang mit Lo verbunden
"1"
a = 0, b = 1
Pull-up-Netzwerk öffnet Pfad zu Hi
Pull-down-Netzwerk hat keinen Pfad zu Lo
Ausgang mit Hi verbunden
Kann man das NAND-Gatter in ein AND-Gatter verwandeln, indem man im
Transistornetzwerk des NAND-Gatters +5V und Masse vertauscht? Nein!
Folie 7-25
Digitale Grundschaltungen
Kondensatoraufladung über nMOS-Transistor
MOS-Transistoren sind keine
idealen Schalter!
UB = +5 V
nMOS im
T1 pullup-Netzwerk?
Im nebenstehenden Beispiel sei die
UGS1
Gatekapazität von T3 (modelliert
T3
durch CG) zunächst ungeladen.
Schließt man das Gate von nMOSTransistor T1 an die BetriebsspanUa
CG
T2
nung UB an, so wird CG aufgeladen,
solange die Spannung Ua an der
0V
Gatekapazität kleiner ist als UB−Uth.
Sobald Ua= UB−Uth, fällt die Spannung UGS1 unter die Schwellspannung Uth und
T1 schaltet ab. Die Aufladung kommt zum Erliegen und die Spannung Ua bleibt
auf dem Wert Ua= UB−Uth.
"Ein nMOS-Transistor leitet den Hi-Pegel nur mit einem
Potentialverlust von Uth weiter."
Folie 7-26
Digitale Grundschaltungen
Kondensatorentladung über nMOS-Transistor
Die Entladung des Kondensators
auf den Lo-Pegel über einen
nMOS-Transistor ist hingegen
ohne Potentialunterschied möglich.
Legt man im nebenstehenden
Beispiel das Gate des Transistors
T1 auf Masse und das Gate von T2
auf die Betriebsspannung, so sperrt
T1 und T2 leitet. Die Gatekapazität
CG der nachfolgenden Stufe T3
wird vollständig auf den
Signalpegel Lo entladen.
UB = +5 V
T1
T3
T2
Ua
CG
0V
nMOS-Transistor im
pulldown-Netzwerk: OK
"Ein nMOS-Transistor leitet den Lo-Pegel ohne
Potentialunterschied weiter."
Folie 7-27
Digitale Grundschaltungen
CMOS-Technologie
Für den pMOS-Transistor gilt Entsprechendes, allerdings jeweils für den
komplementären Signalpegel. Zusammenfassend kann man sagen:
•
•
Ein nMOS-Transistor eignet sich dafür, die 0 weiterzuleiten (aber nicht
die 1), d.h. er eignet sich als pull-down-Transistor.
Ein pMOS-Transistor eignet sich dafür, die 1 weiterzuleiten (aber nicht
die 0), d.h. er eignet sich als pull-up-Transistor.
"Pull-up-Netzwerk":
besteht aus pMOS-Transistoren
"Pull-down-Netzwerk":
besteht aus nMOS-Transistoren
Ein AND-Gatter kann daher in CMOS-Technik nicht einfach durch
Vertauschung von Masse und Betriebsspannung aus einem NAND-Gatter
gewonnen werden.
Ein AND-Gatter muss durch NAND und Inverter realisiert werden.
Komplementärer Aufbau von Pull-up- und Pull-down-Netzwerk:
("complementary MOS", "CMOS")
• Einer Reihenschaltung im pull-up-Netzwerk entspricht eine Parallelschaltung im
pull-down-Netzwerk und umgekehrt.
• Für jede Signalbelegung existiert ein Pfad entweder nach Hi oder nach Lo.
Folie 7-28
Digitale Grundschaltungen
CMOS-Gatter – allgemeiner Aufbau
pMOS
pull-upNetzwerk
Ausgang
y
…
Eingänge
x1
x2
…
UB
…
xn
nMOS
pull-downNetzwerk
0V
Folie 7-29
Digitale Grundschaltungen
CMOS-Komplexgatter
Beispiel:
Implementierung der
Schaltfunktion
UB
a
pull-up-
b
c
Netzwerk
d
y = a ⋅b + c ⋅ d
Komplexgatter:
Schaltung realisiert eine
komplexe Schaltfunktion.
Hier: Funktion genannt
"AND-OR-INVERT-22"
oder
"AOI22"
y
a
pull-down-
c
b
Netzwerk
d
0V
Implementierungsaufwand: 8 Transistoren
Folie 7-30
Digitale Grundschaltungen
CMOS-Komplexgatter
(Beispiel)
Ineffiziente Implementierung derselben Schaltfunktion aus einzelnen
CMOS-Primitivgattern:
AND
a
b
c
d
2
OR
4
2
2
2
4
y
4
AND
Implementierungsaufwand: 20 Transistoren
Mit Komplexgattern (engl. compound gates) lassen sich bestimmte
Funktionen kompakt und effizient implementieren.
Folie 7-31
Digitale Grundschaltungen
Informationsverarbeitung mit digitalen Schaltungen
Beispiel: Schaltung zur Addition von zwei 1-Bit-Dualzahlen
a
„Halbaddierer“:
Eingangssignale: a, b
Ausgangssignale: s (sum), co (carry out)
b
s
Halbaddierer
a
b
co
s
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
co
Folie 7-32
Digitale Grundschaltungen
Beispiel
Beispiel: Schaltung zur Addition von drei 1-Bit-Dualzahlen
„Volladdierer“:
Eingangssignale: a, b, ci (carry in)
Ausgangssignale: s (sum), co (carry out)
a
b
ci
s
Volladdierer
co
a
b
ci
co
s
0
0
0
0
0
0
0
1
0
1
0
1
0
0
1
0
1
1
1
0
1
0
0
0
1
1
0
1
1
0
1
1
0
1
0
1
1
1
1
1
Folie 7-33
Digitale Grundschaltungen
Beispiel
Beispiel: 4-bit-Addierer aus Halb- und Volladdierern
a3
b3
Volladdierer
co,3
ci,3
a2
b2
a1
b1
a0
b0
Volladdierer
Volladdierer
Halbaddierer
co,2
co,1
co,0
ci,2
ci,1
0011
0101
1 1 1
1000
s3
s2
s1
s0
Kleine Funktionseinheiten (Halbaddierer, Volladdierer) werden aus Gattern
zusammengesetzt, größere Funktionseinheiten (4-bit-Addierer) werden aus
kleineren Funktionseinheiten zusammengesetzt.
Folie 7-34
Digitale Grundschaltungen
Aussagenlogische Formeln
Übersetzung der Spezifikation in ein System aussagenlogischer Formeln
Beispiel: Volladdierer
Einfacher Fall: Spezifikation durch Wahrheitstabelle
Aus der Wahrheitstabelle kann man unmittelbar die
kanonische Disjunktive Normalform (DNF) und die
kanonische Konjunktive Normalform (KNF) ablesen.
z.B. kanonische DNF für co:
co = a'bci + ab'ci + abci' + abci
Praxis: Spezifikation durch abstrakte Beschreibung,
sog. „Synthesewerkzeuge“ können aus einer abstrakten
Spezifikation eine Darstellung als System Boolescher
Gleichungen erzeugen.
a
b
ci
co
s
0
0
0
0
0
0
0
1
0
1
0
1
0
0
1
0
1
1
1
0
1
0
0
0
1
1
0
1
1
0
1
1
0
1
0
1
1
1
1
1
Folie 7-35
Digitale Grundschaltungen
Gatternetzliste
co = a'bci + ab'ci + abci' + abci
(kanonische DNF)
Implementierung der kanonischen DNF als Gatternetzliste
a
4 UND-Gatter (3 Eingänge)
1 ODER-Gatter (4 Eingänge)
3 Inverter
b
co
ci
Netz: Verbund elektrisch zusammengeschlossener Drähte
Netzliste: Auflistung aller Gatter-Eingänge und -Ausgänge und der
Netze, mit denen sie verbunden sind
Folie 7-36
Digitale Grundschaltungen
Optimierung
Es gelten die Rechenregeln der Aussagenlogik!
Beispiel: carry-out des Volladdierers
Idempotenz
co = a'bci + ab'ci + abci' + abci
= a'bci + ab'ci + abci' + abci + abci
= a'bci + abci + ab'ci + abci' + abci
= (a' + a)bci + ab'ci + abci' + abci
= (1)bci + ab'ci + abci' + abci
= bci + ab'ci + abci' + abci + abci
= bci + ab'ci + abci + abci' + abci
Für eine systematische Vorgehensweise
benötigen wir
weitere formale
Hilfsmittel !
= bci + a(b'+b)ci + abci' + abci
= bci + a(1)ci + abci' + abci
Assoziativität
= bci + aci + ab(ci' + ci)
= bci + aci + ab(1)
= bci + aci + ab
Folie 7-37
Digitale Grundschaltungen
Gatternetzliste
co = ab + aci + bci
(minimierte DNF)
Implementierung der minimierten DNF
3 UND-Gatter (2 Eingänge)
1 ODER-Gatter (3 Eingänge)
0 Inverter
a
b
co
ci
„zweistufige“ Schaltung
Ebene 1
Ebene 2
Implementierungen, die unmittelbar aus einer DNF oder KNF hervorgehen
heißen „zweistufig“ . Zweistufige Schaltungen besitzen nur zwei „Gatterebenen“,
d.h. Signale durchlaufen von den Eingängen zu den Ausgängen höchstens zwei
Gatter (Inverter werden nicht gezählt).
Folie 7-38
Digitale Grundschaltungen
Gatternetzliste
Liegt eine Formel nicht als DNF oder KNF
vor, spricht man in der Digitaltechnik oft
von einer „faktorisierten“ Form
co = a (b + ci) + bci
Implementierung der faktorisierten Form
2 UND-Gatter (2 Eingänge)
2 ODER-Gatter (2 Eingänge)
0 Inverter
a
b
co
ci
Ebene 1
Ebene 2
„mehrstufige“ Schaltung
Ebene 3
Wie bewerte ich das
zeitliche Verhalten der
Schaltung?
Folie 7-39
Digitale Grundschaltungen
Signallaufzeiten
Alle Schaltvorgänge sind mit einer Verzögerung behaftet!
a
b
i
k
j
ci
co
Annahme:
alle Gatter haben eine
Verzögerungszeit von 1ns
a
b
ci
i
j
k
co
Nach 3ns führt der
Signalwechsel am
Eingang zu dem
entsprechenden
Signalwechsel am
Ausgang
0 ns
1ns
2ns
3ns
Folie 7-40
Digitale Grundschaltungen
Signallaufzeiten
Alle Schaltvorgänge sind mit einer Verzögerung behaftet!
a
b
i
k
j
ci
co
Annahme:
alle Gatter haben eine
Verzögerungszeit von 1 ns
a
b
ci
i
j
k
co
"Glitch": Signale k und co
wechseln kurzeitig den
Wert. Erst nach 3 ns liegt
am Ausgang der korrekte
Wahrheitswert "stabil" an.
0 ns
1ns
2ns
3ns
Folie 7-41
Digitale Grundschaltungen
Glitches und Hazards
Kurze, temporäre Signalwechsel:
Glitch: tatsächlich auftretender temporäre Signalwechsel,
Hazard: Möglichkeit einer Schaltung, einen Glitch zu produzieren (bei
bestimmten Werten der Eingangssignale)
1
1
statischer
1-Hazard
0
1
0
0
1
0
statischer
0-Hazard
Eingangssignalwechsel verursacht
Ausgangssignalwechsel von 1 nach 0 nach 1
Eingangssignalwechsel verursacht
Ausgangssignalwechsel von 0 nach 1 nach 0
1
0
1
0
dynamische Eingangssignalwechsel verursacht doppelten
Wechsel:
1 Hazards
von 0 nach 1 nach 0 nach 1 oder
von 1 nach 0 nach 1 nach 0
0
Folie 7-42
Digitale Grundschaltungen
Hazards und Glitches
•
Hazards führen zu Komplikationen bei der Analyse des Zeitverhaltens einer
Schaltung.
•
Glitches führen zu Komplikationen bei "asynchronen" Schaltungen.
•
Glitches erhöhen die Leistungsaufnahme einer digitalen Schaltung (häufig
um ca. 30 – 50%)
Erinnerung: Aussagenlogik erfasst lediglich das Verhalten digitaler Systeme
im eingeschwungenen (stationären) Zustand.
Folie 7-43
Digitale Grundschaltungen
Analyse des Zeitverhaltens (engl. "timing analysis")
Signalverzögerung einer Schaltung:
Im allgemeinen gilt: Zur Abschätzung der Signalverzögerung einer Schaltung
untersucht man den längsten Pfad. Der längste Pfad ist derjenige Pfad, entlang
dessen die Summe aller Verzögerungen für die Verbindungsleitungen und
Gatterbausteine maximal ist. (Dies gilt auch, falls Glitches auftreten.)
Nimmt man an, dass die Verbindungsleitungen verzögerungsfrei sind und alle
Gatter die gleiche Verzögerungszeit haben, so ist der längste Pfad derjenige Pfad,
der die meisten Gatter durchläuft.
Diese Art der Analyse führt zwar oft zu einer Überschätzung der Signallaufzeiten,
eine genauere Analyse ist aber (auch wegen Hazards) sehr komplex.
Folie 7-44
Digitale Grundschaltungen
Design Trade-offs
Fanin: Anzahl der Eingänge eines Gatters
Fanout: Anzahl der Gatter, die von einem Gatterausgang angesteuert werden
Ziel der meisten Hardwarerealisierungen:
• möglichst geringer Flächenbedarf
(Anzahl der Gatter, Anzahl der Eingänge pro Gatter)
• möglichst schnelle Signallaufzeiten
für die meisten Technologien gilt:
•
•
•
•
•
•
•
Schaltungsfläche beeinflusst Herstellungskosten
Weniger Gatter, weniger Signale ⇒ weniger Fläche
Weniger Gattereingänge ⇒ schnellere Gatter
Maximale Anzahl der Gattereingänge (Fanin) ist beschränkt
Weniger Gatterebenen (Stufen) ⇒ mehr Gatter ⇒ größere Fläche
Weniger Gatterebenen (Stufen) ⇒ schnellere Schaltung
Minimale Signalverzögerung ⇒ mehr Fläche erforderlich
Folie 7-45
Digitale Grundschaltungen
Schaltnetz und Schaltwerk
Bisher haben wir nur Schalternetzwerke betrachtet, deren Ausgangswerte (nach
einer gewissen Verzögerungszeit) allein von den zuletzt angelegten Signalwerten
bestimmt werden.
Beispiel: Addierer
Kombinatorische Schaltung oder Schaltnetz:
Die Ausgangssignale hängen nur von den gegenwärtigen Eingangssignalen ab,
d.h. eine kombinatorische Schaltung bildet eine Signalbelegung an den Eingängen auf eine Signalbelegung an den Ausgängen ab.
Kombinatorische Schaltungen können wir mit den Mitteln der Aussagenlogik
und der Booleschen Algebra beschreiben.
Mit kombinatorischen Schaltungen allein können wir aber noch keinen
Computer bauen…
Folie 7-46
Digitale Grundschaltungen
Schaltnetz und Schaltwerk
Sequenzielle Schaltung oder Schaltwerk:
Die Ausgangssignale hängen von den gegenwärtigen und allen vorangegangenen Eingangssignalen ab (Schaltung hat Gedächtnis), d.h. eine
sequenzielle Schaltung bildet eine Folge von Signalbelegungen an den
Eingängen in eine Folge von Signalbelegungen an den Ausgängen ab.
Auch sequenzielle Schaltungen können durch Netzwerke von Schaltern
realisiert werden.
Beispiele: Steuerung für Ampel mit Kontaktschleife, Prozessor
Sequenzielle Schaltungen werden durch endliche Automaten modelliert. Dazu
später mehr.
Auch sequenzielle Schaltungen können durch Netzwerke von Schaltern
realisiert werden.
Folie 7-47
Technische Informatik I
Kapitel 8
Optimierung von Schaltnetzen
Folie 8-1
Boolesche Funktionen
Optimierung von
Schaltnetzen
Netzwerke logischer Gatter lassen sich durch Boolesche Funktionen beschreiben.
Eine Boolesche Funktion ist eine Abbildung
f : {0, 1}n → {0, 1}
Man kann schreiben: y = f (xn-1, xn-2, ..., x1, x0).
Dabei sind xn-1, xn-2, ..., x1, x0 die n Eingangsvariable der Funktion, und y ist der
Funktionswert bzw. der Ausgang bzw. die Ausgangsvariable der Funktion.
{0, 1}n wird oft als n-dimensionaler Boolescher Raum aufgefasst.
Folie 8-2
Optimierung von
Schaltnetzen
Boolesche Bündelfunktion
Das Verhalten eines digitalen Schaltnetzes kann durch Bündel Boolescher
Funktionen dargestellt werden. Jeder der m Ausgänge yi, 0 ≤ i ≤ m-1, wird durch
eine Boolesche Funktion fi : {0, 1}n → {0, 1} beschrieben.
Alternativ kann das Verhalten des Schaltnetzes auch durch eine (einzelne)
Boolesche Bündelfunktion f : {0, 1}n → {0, 1}m beschrieben werden.
xn-1
xn-2
x0
digitales
Schaltnetz
ym-1
ym-2
y0
Die n Eingangssignale der Schaltung entsprechen den n Eingangsvariablen der
Funktion. Die m Ausgangssignale der Schaltung entsprechen den m
Ausgangsvariablen der Funktion.
Die Signalbelegungen am Eingang der Schaltung entsprechen den Punkten des ndimensionalen Booleschen Raumes {0, 1}n .
Folie 8-3
Optimierung von
Schaltnetzen
Für Boolesche Funktionen können die Formalismen der Aussagenlogik angewendet
werden (siehe Vorlesung Logik, sowie Anhang A). Wir stellen Boolesche Funktionen
durch „Boolesche Ausdrücke“ dar, die entsprechend den Syntaxregeln der
Aussagenlogik aufgebaut sind und verwenden dafür die gleichen Begriffe.
Beispielsweise betrachten wir im folgenden die Disjunktive Normalform (DNF) und
die Konjunktive Normalform (KNF) zur Darstellung Boolescher Funktionen. Auf
eventuelle Begriffsunterschiede zwischen Digitaltechnik und Aussagenlogik weisen
wir gegegebenfalls hin.
Folie 8-4
Disjunktive Normalform
Optimierung von
Schaltnetzen
Definitionen (Monom, DNF, kanonische DNF)
Ein Produktterm oder Monom ist eine Formel von einer der folgenden Formen:
i) 1
ii) ein Literal
iii) eine Konjunktion von Literalen, wobei keine Variable mehr als einmal
auftritt
Eine disjunktive Normalform (DNF) oder
eine Summe von Produkten (engl. sum of products, SOP)
ist eine Formel von einer der folgenden Formen
i) 0
ii) ein Produktterm
iii) eine Disjunktion von Produkttermen
Ein Monom einer SOP für eine Formel f, das für jede in f auftretende Variable
von f ein Literal enthält, heißt Minterm von f. Eine DNF für eine Formel f, die
ausschließlich aus Mintermen besteht, heißt kanonische Mintermform oder
kanonische disjunktive Normalform.
Folie 8-5
Konjunktive Normalform
Optimierung von
Schaltnetzen
Definitionen (Klausel, KNF, kanonische KNF)
Ein Summenterm oder eine Klausel ist eine Formel von einer der folgenden
Formen:
i) 0
ii) ein Literal
iii) eine Disjunktion von Literalen, wobei keine Variable mehr als einmal
auftritt
Ein konjunktive Normalform (KNF) oder ein Produkt von Summen (engl.
product of sums, POS) ist eine Formel von einer der folgenden Formen:
i) 1
ii) ein Summenterm
iii) eine Konjunktion von Summentermen
Eine Klausel einer KNF für eine Formel f, die für jede in f auftretende Variable
ein Literal enthält, heißt Maxterm von f. Eine KNF für eine Formel f, die
ausschließlich aus Maxtermen besteht, heißt kanonische Maxtermform oder
kanonische konjunktive Normalform.
Folie 8-6
Hauptsatz der Schaltalgebra
Optimierung von
Schaltnetzen
Satz (Anhang A)
Für jede aussagenlogische Formel f gibt es eine äquivalente Formel in DNF und
eine äquivalente Formel in KNF.
Entsprechende Formulierung in der Digitaltechnik:
Hauptsatz der Schaltalgebra:
Jede boolesche Funktion f: {0, 1}n → {0, 1} läßt sich als Disjunktion von
Produkttermen (DNF) und Konjunktion von Summentermen (KNF) darstellen.
Also kann eine beliebige Funktion als Schaltnetz realisiert werden, wenn eine
Realisierung für Konjunktion (AND), Disjunktion (OR) und Negation (NOT)
bekannt ist.
Folie 8-7
Optimierung von
Schaltnetzen
Minterme und Maxterme
x1
x2
x3
f
Terme
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
0
1
0
M0 = x1 + x2 + x3
kanonische DNF: f = m1 + m3 + m6
m1 = x1’ ⋅ x2’ ⋅ x3
M2 = x1 + x2’ + x3
m3 = x1’ ⋅ x2 ⋅ x3
M4 = x1’ + x2 + x3
M5 = x1’ + x2 + x3’
m6 = x1 ⋅ x2 ⋅ x3’
M7 = x1’ + x2’ + x3’
kanonische KNF: f = M0·M2·M4·M5·M7
Kurzschreibweise: f(x1, x2, x3) = Σm(1,3,6) Kurzschreibweise: f(x1, x2, x3) = ΠM(0,2,4,5,7)
Kanonische DNF und KNF können auch als Mengen von Mintermen bzw.
Maxtermen aufgefasst werden. Die kanonische DNF enthält die Minterme, die zu
den Einsstellen der Funktion gehören, die sog. Einsstellenminterme, die
kanonische KNF enthält die Maxterme, die zu den Nullstellen der Funktion
gehören, die sog. Nullstellenmaxterme.
Folie 8-8
Optimierung von
Schaltnetzen
Zweistufige Boolesche Darstellungen
Summe von Produkten, Produkte von Summen und DeMorgan-Regel
Beispiel:
f' = a'b'c' + a'b'c + a'bc'
berechne f aus f' mit DeMorgan-Regel:
(f')' = (a'b'c' + a'b'c + a'bc')'
f = (a + b + c) (a + b + c') (a + b' + c)
f' = (a + b' + c' )(a' + b + c)(a' + b + c')(a' + b' + c)(a' + b' + c')
berechne f aus f' mit DeMorgan-Regel:
(f')' = {(a + b' + c')(a' + b + c)(a' + b + c')(a' + b' + c)(a' + b' + c')}'
f = a'bc + ab'c' + ab'c + abc' + abc
Folie 8-9
Zweistufige Boolesche Darstellungen
Optimierung von
Schaltnetzen
Vier alternative zweistufige
Implementierungen von f:
a
b
f1
c
kanonische DNF
(Minterme)
minimierte DNF
f2
kanonische KNF
(Maxterme)
f3
minimierte KNF
f4
Folie 8-10
Zweistufige Boolesche Darstellungen
Optimierung von
Schaltnetzen
Umwandlungen zwischen zweistufigen Darstellungsarten
1.
kanonische DNF in kanonische KNF:
übertrage Mintermkurzschreibweise in Maxtermkurzschreibweise,
ersetze die Mintermindizes durch die nicht aufgetretenen Indizes
z.B.: f(a,b,c) = Σm(3,4,5,6,7) = ΠM(0,1,2)
2.
kanonische KNF in kanonische DNF:
übertrage Maxtermkurzschreibweise in Mintermkurzschreibweise,
ersetze die Maxtermindizes durch die nicht aufgetretenen Indizes
z.B.: f(a,b,c) = ΠM(0,1,2) = Σm(3,4,5,6,7)
Folie 8-11
Zweistufige Boolesche Darstellungen
Optimierung von
Schaltnetzen
Umwandlungen zwischen zweistufigen Darstellungsarten
3.
kanonische DNF (KNF) von f in kanonische DNF (KNF) von f':
in Mintermkurzschreibweise: liste alle in f noch nicht benutzten Indizes auf
z.B.: f(a,b,c) = Σm(3,4,5,6,7)
= ΠM(0,1,2)
4.
f'(a,b,c) = Σm(0,1,2)
= ΠM(3,4,5,6,7)
kanonische DNF(KNF) von f in kanonische KNF(DNF) von f':
übertrage in Maxtermkurzschreibweise, nehme gleiche Indizes wie in f
z.B.: f(a,b,c) = Σm(3,4,5,6,7)
= ΠM(0,1,2)
f'(a,b,c) = ΠM(3,4,5,6,7)
= Σm(0,1,2)
Folie 8-12
Terminologie
Optimierung von
Schaltnetzen
In der Digitaltechnik ist die folgende Terminologie üblich:
• eine KNF heißt auch Produkt von Summen (POS)
• eine DNF heißt auch Summe von Produkten (SOP)
Definition: (Implikant)
Ein Monom (=Produktterm) p, d.h. eine Konjunktion von Literalen, heißt
Implikant für eine Funktion f, genau dann wenn gilt:
p=1⇒f=1
Man sagt, ein Monom p1 "überdeckt" ein Monom p2, wenn p2 = 1 ⇒ p1 = 1
gilt.
Beispiel: f = abc + a'bc + ad + be + cf
Offensichtlich sind abc, a'bc, ad, be, cf Implikanten für f. Die Funktion f
überdeckt ihre Implikanten. Es gibt aber noch weitere Implikanten, z.B. bc.
Der Implikant bc überdeckt den Implikanten abc.
Folie 8-13
Terminologie
Optimierung von
Schaltnetzen
Definition: (Primimplikant)
Ein Implikant heißt Primimplikant für eine Funktion f, wenn jeder Produktterm,
der durch Wegstreichen eines Literals des Implikanten entsteht, kein Implikant
für f ist.
Ein Primimplikant ist also ein Implikant, der von keinem anderen Implikanten
überdeckt wird.
Beispiel: f = abc + abc'
abc ist kein Primimplikant von f, denn durch Wegstreichen von c entsteht der
Produktterm ab, der ebenfalls Implikant ist. Der Implikant ab ist ein Primimplikant,
denn weder a noch b sind Implikanten.
Terminologie für den dualen Fall:
Man bezeichnet einen Summenterm q als Implikat für f, genau dann wenn gilt:
f = 1 ⇒ q = 1. Ein Implikat heißt Primimplikat für eine Funktion f, wenn jeder
Summenterm, der durch Wegstreichen eines Literals des Implikats entsteht, kein
Implikat für f ist.
Folie 8-14
Bestandsaufnahme
Optimierung von
Schaltnetzen
Schaltnetzentwurf
Bisher wurden die folgenden Schritte zum Entwurf eines digitalen
Schaltnetzes betrachtet
Spezifikation des Schaltnetzentwurfs durch Wahrheitstabelle
Ableiten der kanonischen DNF oder kanonischen KNF
Umformung durch Anwendung der Rechenregeln der Booleschen
Algebra (oder Aussagenlogik)
offene Fragen:
• systematische Vorgehensweise zur Optimierung von zweistufigen oder
mehrstufigen Schaltungen
• Anpassung der Schaltung an die vorhandenen Gattertypen
Folie 8-15
Zweistufige Schaltungen
Optimierung von
Schaltnetzen
Betrachte hier die Optimierung von zweistufigen Schaltungen:
• zweistufige Schaltungen haben in der Regel kurze Signallaufzeiten
• für zweistufige Schaltungen existiert eine systematische Vorgehensweise,
die auch bei mehrstufigen Schaltungen eine Rolle spielt
• für zweistufige Schaltungen existieren kostengünstige
Implementierungsstile
Ziel der zweistufigen Minimierung:
SOP oder POS mit minimaler Anzahl von Produkt- bzw. Summentermen. (Unter
den Darstellungen mit gleicher Anzahl von Produkt- bzw. Summentermen wähle
diejenige mit den wenigsten Literalen.)
Folie 8-16
Optimierung von
Schaltnetzen
Beispiel
Carry-out des Volladdierers (Wdh. aus Kap. 7)
Minterme können gemäß folgender
Regel zusammengefasst werden:
x'y + xy = y
co = a'bci + ab'ci + abci' + abci
= a'bci + ab'ci + abci' + abci + abci
= a'bci + abci + ab'ci + abci' + abci
= (a' + a)bci + ab'ci + abci' + abci
= (1)bci + ab'ci + abci' + abci
= bci + ab'ci + abci' + abci + abci
= bci + ab'ci + abci + abci' + abci
= bci + a(b'+b)ci + abci' + abci
= bci + a(1)ci + abci' + abci
= bci + aci + ab(ci' + ci)
Vermutung:
wiederholte Anwendung dieser
Regel kann offensichtlich
wichtiger Bestandteil eines
Optimierungsverfahrens für
zweistufige Schaltungen sein
= bci + aci + ab(1)
= bci + aci + ab
systematische Vorgehensweise?
Folie 8-17
Zusammenfassen von Monomen
Optimierung von
Schaltnetzen
naheliegende Idee für Optimierungsverfahren:
fasse Minterme zu möglichst wenigen Monomen (Produkttermen) zusammen.
Zwei Monome mi und mj können genau dann zu einem einzigen Monom m*
zusammengefasst werden, wenn
mi = mj (Spezialfall, Anwendung der Idempotenzregel)
oder
mi ≠ mj und Regel x'y + xy = y anwendbar ist.
Für das neue Monom m* gilt dann: m* = mi + mj
Folie 8-18
Zweistufige Minimierung
Optimierung von
Schaltnetzen
Gegeben sei eine Boolesche Funktion f in kanonischer DNF.
Betrachte die Menge aller Einsstellen-Minterme F = { m1, m2, …} von f
und die Relation
"kann zu einem Monom zusammengefasst werden",
d.h.
R = {(mi, mj) | mi, mj ∈ F und
mi + mj = y wobei y ein beliebiges Monom ist}.
Welchen Typs ist R?
reflexiv?
ja,
denn mi + mi = mi (Idempotenz) für alle Monome mi ∈ F
symmetrisch?
ja,
denn mi + mj = mj + mi für alle mi, mj ∈ F
transitiv?
nein,
Gegenbeispiel: mi = ab, mj = ab', mk = a'b'
⇒ Verträglichkeitsrelation
Folie 8-19
Zweistufige Minimierung
Optimierung von
Schaltnetzen
Minterme, die zu einem einzigen Monom zusammengefasst werden können, stehen
in einer Verträglichkeitsrelation zueinander.
⇒
zu einem Monom zusammenfassbare Minterme bilden eine
Verträglichkeitsklasse
⇒
jeder Minterm ist in einer Verträglichkeitsklasse enthalten
⇒
die Verträglichkeitsklassen können sich "überlappen"
⇒
gesucht sind Mengen von Verträglichkeitsklassen, die eine Überdeckung
der Menge aller Minterme darstellen
Folie 8-20
Zweistufige Minimierung
Optimierung von
Schaltnetzen
Die Rechenregel x'y + xy = y kann nicht nur auf Minterme, sondern iterativ auch
auf die durch diese Regel entstehenden Monome angewendet werden.
Definition
Sei F eine Menge von Monomen. Dann ist Conss(F) definiert als
Conss(F) = F ∪ {y | zwei Monome von der Form x'y und xy in F
existieren}
Außerdem schreiben wir:
Conss0(F) = F
Conssn+1(F) = Conss(Conssn(F)) für n ≥ 0.
Und schließlich sei
Conss*(F) =
U Conssn(F)
n≥0
Folie 8-21
Zweistufige Minimierung
Optimierung von
Schaltnetzen
Durch die iterative Anwendung der Regel x'y + xy = y können auch mehr als zwei
Minterme zu einem Monom zusammengefasst werden.
Gilt für Minterme m1, m2, …, mk, dass m1 + m2 + … + mk = y, wobei y ein Monom
ist, dann wird jedes mi, i = 1, 2, …, k, und keine weiteren Minterme durch y
überdeckt.
Beachte: k ist immer eine Zweierpotenz
Gegeben sei eine Boolesche Funktion f in kanonischer DNF.
Betrachte die Menge aller Minterme F = {m1 m2 …} von f und die
Verträglichkeitsrelation
R* = "werden von dem gleichen Monom y, y ∈Conss*(F) überdeckt",
d.h.
R* = {(mi, mj) | mi, mj ∈ F
und es existiert ein y ∈Conss*(F) mit mi ⇒ y und mj ⇒ y}
Folie 8-22
Zweistufige Minimierung
Optimierung von
Schaltnetzen
Die minimale DNF erhält man wie folgt:
1)
2)
3)
bestimme Conss*(F)
bestimme die Menge der maximalen Verträglichkeitsklassen τ = {C1, C2…}
bezüglich R*
bestimme eine Teilmenge τ' von τ, die F überdeckt und eine minimale
Anzahl von Elementen aus τ enthält.
Es gilt:
Die Verträglichkeitsklassen entsprechen den Implikanten,
die maximalen Verträglichkeitsklassen entsprechen den Primimplikanten der
Funktion.
Die minimale DNF besteht dann gerade aus den Primimplikanten, die zu einer
minimalen Überdeckung τ' gehören.
Folie 8-23
Zweistufige Minimierung
Satz von Quine:
Optimierung von
Schaltnetzen
Eine minimale Summe von Produkten für eine
boolesche Funktion besteht ausschließlich aus
Primimplikanten.
Es müssen also nur die maximalen Verträglichkeitsklassen betrachtet werden.
Zur Minimierung einer zweistufigen Schaltung sind also die folgenden Schritte
notwendig:
1) Bestimmung der Primimplikanten der Funktion
2) Bestimmung einer minimalen Überdeckung aller Einsstellen-Minterme
durch die Primimplikanten
Diese Vorgehensweise wurde erstmals durch C. Quine und E. McCluskey in den
50-er Jahren vorgeschlagen und ist als "Quine-McCluskey-Methode" bekannt.
Folie 8-24
Quine-McCluskey-Methode
Optimierung von
Schaltnetzen
Phase 1: Bestimmung der Primimplikanten:
gegeben: kanonische DNF für Funktion f
gesucht: alle Primimplikanten
Lösung:
- berechne Conss*(F) (enthält alle Verträglichkeitsklassen)
- bestimme die maximalen Verträglichkeitsklassen durch Streichung
alle Verträglichkeitsklassen, die in anderen enthalten sind
Eine tabellarische Darstellung erleichtert die systematische Durchführung dieser
Schritte.
Folie 8-25
Optimierung von
Schaltnetzen
Quine-McCluskey-Methode
Tabellarische Methode zur systematischen Bestimmung der Primimplikanten
ƒ(a, b, c ,d) = Σm(0, 4, 5, 6, 7, 8, 9, 10, 13, 15)
Schritt 1: trage in Spalte 1 die binär dargestellten
Indizes aller Einsstellen-Minterme von f,
sortiert nach Anzahl der Einsen, ein.
Implikantentabelle
Spalte 1
0000
0100
1000
0101
0110
1001
1010
0111
1101
1111
Folie 8-26
Optimierung von
Schaltnetzen
Quine-McCluskey-Methode
Tabellarische Methode zur systematischen Bestimmung der Primimplikanten
ƒ(a, b, c ,d) = Σm(0, 4, 5, 6, 7, 8, 9, 10, 13, 15)
Schritt 1: trage in Spalte 1 die binär dargestellten
Indizes aller Einsstellen-Minterme von f,
sortiert nach Anzahl der Einsen, ein.
Implikantentabelle
Spalte 1
0000 √
Schritt 2: fasse Terme zusammen:
Vergleiche Elemente von Gruppen mit n
und n+1 Einsen. Ist nur 1 Bit verschieden,
sind sie benachbart. Eliminiere Variable
und trage Term in nächste Spalte ein.
z.B.: 0000 und 0100 ergibt 0-00
0000 und 1000 ergibt -000
Markiere zusammengefasste Terme mit √,
nicht zusammengefasste mit *. Mit *
markierte Terme sind Primimplikanten,
0100 √
1000 √
0101
0110
1001
1010
√
√
√
√
0111 √
1101 √
1111 √
Spalte 2
0-00
-000
01001-0
10010-0
01-1
-101
0111-01
-111
11-1
Wiederhole, bis keine Terme mehr
zusammengefasst werden können.
Folie 8-27
Optimierung von
Schaltnetzen
Quine-McCluskey-Methode
Tabellarische Methode zur systematischen Bestimmung der Primimplikanten
ƒ(a, b, c ,d) = Σm(0, 4, 5, 6, 7, 8, 9, 10, 13, 15)
Schritt 1: trage in Spalte 1 die binär dargestellten
Indizes aller Einsstellen-Minterme von f,
sortiert nach Anzahl der Einsen, ein.
Implikantentabelle
Spalte 1
0000 √
Schritt 2: fasse Terme zusammen:
Vergleiche Elemente von Gruppen mit n
und n+1 Einsen. Ist nur 1 Bit verschieden,
sind sie benachbart. Eliminiere Variable
und trage Term in nächste Spalte ein.
z.B.: 0000 und 0100 ergibt 0-00
0000 und 1000 ergibt -000
Markiere zusammengefasste Terme mit √,
nicht zusammengefasste mit *. Mit *
markierte Terme sind Primimplikanten,
0100 √
1000 √
0101
0110
1001
1010
√
√
√
√
0111 √
1101 √
1111 √
Spalte 2
0-00 *
-000 *
Spalte 3
01-- *
-1-1 *
01001-0
10010-0
√
√
*
*
01-1
-101
0111-01
√
√
√
*
-111 √
11-1 √
Wiederhole, bis keine Terme mehr
zusammengefasst werden können.
Folie 8-28
Bestimmung der Primimplikanten
Optimierung von
Schaltnetzen
Nachteil dieser Methode:
Ausgangspunkt ist die kanonische DNF (oder kanonische KNF). Die Anzahl der
Minterme bzw. Maxterme einer Funktion wächst im allgemeinen exponentiell
mit der Anzahl der Variablen. Rechenzeit! Speicherbedarf!
Folie 8-29
Bestimmung der Primimplikanten
Optimierung von
Schaltnetzen
Wie bestimmt man alle Primimplikanten, wenn eine (nicht-kanonische) DNF
oder KNF gegeben ist?
Bei der Berechnung von Conss* wurde die Rechenregel
x'y + xy = x'y + xy + y
benutzt.
Beobachtung: dies ist ein Spezialfall der sog. "Konsensusregel"
x'y + xz = x'y + xz + yz
(Spezialfall: y = z.)
Dualer Fall: (x' + y)(x + z) = (x' + y)(x + z)(y + z)
(bekannt aus der Vorlesung Logik als Resolutionsregel der
Aussagenlogik, bzw. siehe Anhang A.)
Folie 8-30
Optimierung von
Schaltnetzen
Bestimmung der Primimplikanten
Erkenntnis: der aus der Aussagenlogik bekannte Resolutionskalkül hat in der
Digitaltechnik noch eine andere nützliche Interpretation:
Bestimmung aller Primimplikanten oder Primimplikate ausgehend von einer
beliebigen DNF bzw. KNF
In Aussagenlogik und Digitaltechnik sind unterschiedliche Begriffe
gebräuchlich, obwohl die zugrunde liegenden Formalismen oft identisch sind.
x'y + xz = x'y + xy + yz
(x' + y)(x + z) = (x' + y)(x + z)(y + z)
"Konsensusterm"
"Resolutionsregel" oder "Konsensusregel"
Folie 8-31
Aussagenlogik und Digitaltechnik
Aussagenlogik
Optimierung von
Schaltnetzen
Digitaltechnik
"Resolutionsregel"
"Konsensusregel"
Darstellung grundlegender
Konzepte in der Literatur
meist auf Basis von KNF
Darstellung grundlegender
Konzepte in der Literatur
meist auf Basis von DNF
"Resolutionskalkül"
"Verfahren des iterativen Konsensus"
"Resolvente"
"Konsensusterm"
ziehe alle Schlussfolgerungen
berechne Primimplikanten
(oder Primimplikate)
Folie 8-32
Verfahren des iterativen Konsensus
Optimierung von
Schaltnetzen
Schreibweise: wir betrachten eine Funktion f dargestellt als DNF. Die Menge der in
dieser DNF-Darstellung enthaltenen Monome bezeichnen wir im folgenden
ebenfalls mit "f".
Wdh.:
(s. Anhang A)
Res(f) = f ∪ {r | r ist Resolvente zweier Klauseln in f}
dualer Fall:
Cons(f) = f ∪ {r | r ist Konsensusterm zweier Monome in f}
also:
Cons(f) = f ∪ {yz | es existieren zwei Monome von der Form
x'y und xz in f}
Cons*(f) sei analog zu Conss*(f) definiert. Dann enthält Cons*(f) alle
Primimplikanten von f.
Folie 8-33
Verfahren des iterativen Konsensus
Optimierung von
Schaltnetzen
Berechnung der Primimplikanten einer Funktion f, die als DNF dargestellt ist:
1. berechne die Konsensusterme für alle bislang noch nicht untersuchten
Paare von Produkttermen und füge sie zur SOP hinzu
2. streiche alle Terme, die von anderen Termen überdeckt werden.
wiederhole 1. und 2., bis keine neuen Konsensusterme mehr entstehen.
Die Produktterme der DNF sind dann die Primimplikanten von f.
Entspricht Resolutionskalkül der Aussagenlogik!
Folie 8-34
Überdeckungsproblem
Optimierung von
Schaltnetzen
Quine-McCluskey-Methode
Phase 2: Lösung des Überdeckungsproblems:
gegeben: die Einsstellenminterme und die Primimplikanten der Funktion f
gesucht: eine Menge von Primimplikanten, die alle Einsstellen und keine
Nullstellen der Funktion bei optimalen Kosten überdeckt
Lösung:
mittels Überdeckungsmatrix:
Die Überdeckungsmatrix A = (aij) ist eine Matrix, die angibt, wie die
Einsstellenminterme mi der Funktion f von den Primimplikanten pj überdeckt
werden. Jede Spalte der Matrix entspricht einem Einsstellenminterm mi von f und
jede Zeile entspricht einem der Primimplikanten pj von f. Ein Element aij der
Matrix hat den Eintrag x, falls mi von pj überdeckt wird. Sonst hat A keine
Einträge.
Folie 8-35
Optimierung von
Schaltnetzen
Überdeckungsproblem
Beispiel:
zu überdeckende Minterme: m4, m5, m6, m8, m9, m10, m13
(wir wollen also in diesem Fall nicht alle Minterme aus dem
vorigen Beispiel überdecken, dazu später mehr)
Primimplikanten: wie im vorigem Beispiel
0-00
-000
10010-0
1-01
01--1-1
4
x
5
6
8
9
x
x
x
x
x
x
13
x
x
x
10
x
x
x
Überdeckungsmatrix
Folie 8-36
Optimierung von
Schaltnetzen
Überdeckungsproblem
Lösung des Überdeckungsproblems durch Überdeckungsmatrix
0-00
-000
10010-0
1-01
01--1-1
4
x
5
6
8
9
x
x
x
x
x
x
13
x
x
x
10
x
x
x
Beobachtung: m6 und m10 werden nur von den Primimplikanten 10-0 und 01-überdeckt. Sie müssen also notwendigerweise in jeder Überdeckung enthalten
sein.
Definition: (Kernimplikant)
Wird eine Einsstelle nur von einem einzigen Primimplikanten überdeckt,
heißt dieser Kernimplikant.
streiche Kernimplikanten
Folie 8-37
Optimierung von
Schaltnetzen
Überdeckungsproblem
Lösung des Überdeckungsproblems durch Überdeckungsmatrix
0-00
-000
10010-0
1-01
01--1-1
4
x
5
6
8
9
x
x
x
x
10
x
x
x
x
x
13
x
x
x
streiche von Kernimplikanten überdeckte Minterme
Dies ist die 1. Regel zur Reduktion der Überdeckungsmatrix
Folie 8-38
Optimierung von
Schaltnetzen
Überdeckungsproblem
Lösung des Überdeckungsproblems durch Überdeckungsmatrix
pj
pi
0-00
-000
10010-0
1-01
01--1-1
4
x
5
6
8
9
x
x
x
x
10
x
x
x
x
x
13
x
x
x
2. Regel zur Reduktion einer Überdeckungsmatrix
Zeilendominanz
Sei pi eine Zeile, die alle Einträge einer Zeile pj enthält. Außerdem seien die
Kosten für pi nicht größer als die Kosten für pj. Dann kann die Zeile pj
entfernt werden.
(Kosten eines Primimplikanten: Anzahl der Literale)
Folie 8-39
Optimierung von
Schaltnetzen
Überdeckungsproblem
3. Regel zur Reduktion einer Überdeckungsmatrix: Spaltendominanz
Hat eine Spalte si einer Überdeckungsmatrix in allen Zeilen einen Eintrag, für die
auch eine Spalte sj einen Eintrag besitzt, dann wird Spalte si von Spalte sj dominiert
und kann entfernt werden.
0-00
-000
10010-0
1-01
01--1-1
4
x
5
6
8
9
x
x
x
x
x
x
13
x
x
x
10
x
x
x
Beachte: In diesem Beispiel bestimmen die Reduktionsregeln allein bereits
eindeutig eine Menge von Primimplikanten, die alle Einsstellenminterme
überdecken. Im allgemeinen können jedoch nicht überdeckte Einsstellen
übrigbleiben. Es müssen dann alle möglichen Überdeckungen untersucht
und die günstigste identifiziert werden.
(⇒ Algorithmen zur Lösung von Überdeckungsproblemen)
Folie 8-40
Optimierung von
Schaltnetzen
Überdeckungsproblem
noch ein Beispiel:
1
2
3
4
5
6
1
X
X
2
X
X
3
4
X
X
X
X
X
X
5
6
X
X
X
X
X
Annahme:
Kosten für 1 und 3 kleiner als Kosten für 2
Kosten für 4 gleich Kosten für 5
Folie 8-41
Optimierung von
Schaltnetzen
Überdeckungsproblem
1
2
3
4
5
6
1
X
X
2
X
X
3
4
X
X
X
X
X
X
⇓
Annahme:
Kosten für 1 und 3
kleiner als Kosten für 2 1
2
Kosten für 4 gleich
3
Kosten für 5
4
5
2
X
X
3
5
X
X
X
X
5
6
X
X
X
X
X
Das Überdeckungsproblem ist ein
"Standardproblem" der Informatik,
für dessen Lösung eine Reihe von
Algorithmen existieren.
Zeilendominanz
nach iterativer Anwendung aller Reduktionsregeln
keine weitere Vereinfachung möglich!
Folie 8-42
Boolesche Würfel
Optimierung von
Schaltnetzen
Im folgenden werden wir Boolesche Funktionen durch Würfel beschreiben. Es wird
eine spezielle Darstellung Boolescher Würfel, sog. Karnaugh-Veitch (KV)Diagramme, eingeführt.
Beachte !!
KV-Diagramme dienen hauptsächlich der Veranschaulichung der vorstehend
beschriebenen Vorgehensweise. Industrielle Optimierungsverfahren beruhen nicht
auf KV-Diagrammen! Stattdessen verwenden sie abgewandelte Versionen der
Quine-McCluskey-Methode, die nicht immer das exakte Minimum finden, dafür
aber gegenüber der exakten Methode Rechenzeit einsparen.
KV-Diagramme eignen sich also nicht als Grundlage für CAD-Werkzeuge. Sie
erlauben uns allenfalls, manuell kleine Beispiel mit bis zu 6 Variablen zu
untersuchen.
Folie 8-43
Optimierung von
Schaltnetzen
Boolesche Würfel
0
1
XYZ
111
011
X
1-dimensionaler Würfel
010
XY
11
01
110
Y
Y
00
noch eine Möglichkeit
zur Darstellung einer
Booleschen Funktion
001
Z
101
000
10
100
X
X
n Eingangsvariable ⇒
n-dimensionaler „Würfel“
3-dimensionaler Würfel
2-dimensionaler Würfel
WXYZ
1011
1111
0111
0011
1010
1110
0010
0110
Y
1001
0101
0001
1101
Z
1100
W
0000
X
1000
0100
4-dimensionaler Würfel
Folie 8-44
Optimierung von
Schaltnetzen
Boolesche Würfel
Boolesche Funktion: Abbildung der Punkte des Booleschen Raums auf 1 oder 0
Einsstellenmenge : ausgefüllte Knoten
Nullstellenmenge: nicht ausgefüllte Knoten
Würfel der Dimension 1
f
01
11
a ist 1
b variiert
b
00
10
g = (a + a')b' = b'
a
f = a(b + b') = a
g
01
11
b
a variiert
b ist 0
00
10
a
Folie 8-45
Optimierung von
Schaltnetzen
Boolesche Würfel
Beispiel mit 3 Variablen: Carry-Out des Volladdierers
(a' + a)bcin
011
a b cin
cout
0
0
1
1
0
0
1
1
0
0
0
1
0
1
1
1
0
0
0
0
1
1
1
1
0
1
0
1
0
1
0
1
111
010
110
001
b
101
cin
000
a
ab(cin' + cin)
Die Einsstellenmenge
wird von Teilwürfeln
niedrigerer Dimension
überdeckt
100
a(b + b')cin
cout = bcin + ab + acin
Folie 8-46
Optimierung von
Schaltnetzen
Boolesche Würfel
Teilwürfel mit Dimension größer 1
f(a,b,c) = Σm(4,5,6,7)
011
111
Einsstellenmenge bildet eine rechteckige Fläche,
d.h. einen zweidimensionalen Würfel
010
110
b
stellt einen Ausdruck mit einer Variablen dar
(3 Dimensionen - 2 Dimensionen)
001
101
c
000
a
100
a ist 1
b und c variieren
Diesen Teilwürfel
repräsentiert der Implikant a
Folie 8-47
Boolesche Würfel
Optimierung von
Schaltnetzen
in einem 3-dimensionalen Booleschen Raum:
entspricht ein 0-dimensionaler Würfel einem Produktterm mit 3 Literalen
entspricht ein 1-dimensionaler Würfel einem Produktterm mit 2 Literalen
entspricht ein 2-dimensionaler Würfel einem einzelnen Literal
entspricht ein 3-dimensionaler Würfel dem konstanten Term 1
allgemein:
ein m-dimensionaler Teilwürfel in einem n-dimensionalen booleschen
Raum (n-dimensionaler Würfel) (m < n) entspricht einem Produktterm mit
n - m Literalen
Optimierungsstrategie:
fasse alle Einsstellen (und keine Nullstellen) in möglichst
wenig Teilräumen mit möglichst großer Dimension zusammen
Folie 8-48
Boolesche Würfel
Optimierung von
Schaltnetzen
Stellt man Boolesche Funktionen als Mengen von Würfeln im Booleschen Raum
dar, ergibt sich aus der Anschauung die folgende Optimierungsstrategie
Optimierungsstrategie:
1) fasse alle Einsstellen (und keine Nullstellen) in möglichst
wenig Teilräumen mit möglichst großer Dimension zusammen
→ diese entsprechen den Primimplikanten der Funktion
2) bestimme eine Menge von Würfeln, die alle Einsstellen kostenminimal
überdeckt
Anschaulich, aber schwierig: Würfel mit mehr als 3 Dimensionen kann man nicht
zeichnen!
Ein KV-Diagramm ist eine modifizierte Würfeldarstellung, die für bis zu 6
Dimensionen praktikabel ist.
Folie 8-49
Optimierung von
Schaltnetzen
Kanaugh-Veitch (KV)-Diagramme (K-map)
a
0
b
KV-Diagramm
mit 2 Variablen
1
1
00
cd
0
0
1
a
ab
2
00
01
11
10
0
4
12
8
1
5
13
9
3
7
15
11
2
6
14
10
3
01
a
ab
c
KV-Diagramm
mit 3 Variablen
00
01
11
11
10
10
0
1
c
0
2
6
4
1
3
7
5
b
d
KV-Diagramm
mit 4 Variablen
b
Zählschema: 00, 01, 11, 10
(Gray Code — nur ein Bit ändert sich von einem
Codewort zum nächsten)
KV-Diagramme können auf unterschiedliche Weise gezeichnet werden!
(siehe Übung)
Folie 8-50
Optimierung von
Schaltnetzen
KV-Diagramme
ab
00
c
01
11
111
011
a
10
010
0
000
010
110
100
1
001
011
111
101
110
b
001
101
c
b
000
a
100
"Abwickeln" eines Würfels
in KV-Diagramm
Folie 8-51
Optimierung von
Schaltnetzen
KV-Diagramme
a
0
1
0
0
1
1
0
1
b
a
0
1
0
1
1
1
0
0
b
a fest
b variiert
b fest
a variiert
f=a
g = b'
a
ab
00
cin
01
11
c
0
1
0
0
0
1
1
1
b
cout = ab + bcin + acin
a
ab
10
00
01
11
10
0
0
0
1
1
1
0
0
1
1
0
1
b
f(a, b, c) = a
Folie 8-52
Optimierung von
Schaltnetzen
KV-Diagramme
a
ab
01
00
c
0
1
0
0
1
11
0
0
2
4
1
3
f(a, b, c) = Σm(0,4,5,7)
1
6
0
1
10
1
7
5
b
ab
c
f = b'c' + ac
Im KV-Diagramm reichen Nachbarschaften
auch von links nach rechts und von oben
nach unten
a
00
01
11
10
0
0
1
1
0
1
1
0
1
1
2
0
3
6
7
0
f': ersetze Einsstellen durch Nullstellen
4
f'(a, b, c) = Σm(1,2,3,6)
5
f' = bc' + a'c
b
Folie 8-53
Optimierung von
Schaltnetzen
KV-Diagramme
a
ab
00
01
11
10
00
1
0
0
1
01
0
1
0
0
cd
f(a, b, c, d) = Σm(0, 2, 3, 5, 6, 7, 8, 10, 11, 14, 15)
f = c + a'bd + b'd'
überdecke die Einsstellen
mit möglichst wenigen und
möglichst großen Teilwürfeln
d
11
1
1
1
1
10
1
1
1
1
c
b
1011
1111
0111
0011
1010
1110
0010
0110
1001
c
d
0000
1100
a
b
1101
0101
0001
Illustration von Nachbarschaften
in 4-dimensionalem KV-Diagramm
1000
0100
Folie 8-54
Optimierung von
Schaltnetzen
KV-Diagramme
bc
bc
de
00
a =0
01
01
11
10
0
4
12
8
1
11
10
00
5
3
7
2
6
13
15
14
a=0
9
1
01
11
10
00
01
11
16
20
28
17
19
18
1
1
bc
de
00
10
1
1
10
10
11
1
11
11
01
1
01
bc
a =1
00
de
00
21
23
22
29
31
30
24
a=1
26
KV-Diagramm mit 5 Variablen
11
1
01
11
10
1
1
1
01
25
27
00
de
00
10
1
1
1
10
ƒ(a,b,c,d,e) = Σm(2,5,7,8,10,
13,15,17,19,21,23,24,29 31)
= ce + ab'e + bc'd'e'
+ a'c'de'
Folie 8-55
Optimierung von
Schaltnetzen
KV-Diagramm
cd
ef
cd
ef
00
ab =00
01
01
11
10
0
4
12
8
1
11
10
00
5
3
7
2
6
13
15
14
11
00
ab =01
01
11
10
01
11
16
20
28
19
18
21
23
22
11
10 1
cd
ef
00
00
ab =01
29
31
30
10
24
25
27
ƒ(a, b, c, d, e, f) =
Σm(2,8,10,18,24,26,34,
37,42,45,50,53,58,61)
ab =11
01
11
10
01
11
48
52
60
49
51
50
53
55
54
61
63
62
10
ab =10
00
01
10 1
11
10
35
34
1
32
36
44
37
39
38
45
47
46
10
40
43
42
1
01
10
41
01
11
10
1
11
58
11
00
00
ab =11
56
59
01
33
= d'ef' + ade'f+ a'cd'f'
57
00
10
1
cd
cd
ef
11
11
26
00
01
01
cd
00
1
ef
ef
10
1
10
00
17
11
01
cd
ef
01
00
ab =00
KV-Diagramm
mit 6 Variablen
9
00
Selbst für geübte
Designer wird es jetzt
unübersichtlich!
1
1
cd
ef
00
01
11
00
ab =10
01
1
1
11
10
1
1
Folie 8-56
10
Unvollständig spezifizierte Funktionen
Optimierung von
Schaltnetzen
Funktionen mit n Variablen haben 2n mögliche Eingangsbelegungen.
Für eine gegebene Funktion können möglicherweise nicht alle
Kombinationen auftreten oder nicht alle Kombinationen sind von
Interesse. Dies kann bei der Minimierung ausgenutzt werden!
z.B.: Inkrementieren einer binär kodierten Dezimalziffer (BCD)
BCD (binary coded decimal)-Ziffern kodieren
die Dezimalziffern 0 - 9 mit den Bitmustern
00002 - 10012
a
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
b
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
c
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
d
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
w
0
0
0
0
0
0
0
1
1
0
X
X
X
X
X
X
x
0
0
0
1
1
1
1
0
0
0
X
X
X
X
X
X
y
0
1
1
0
0
1
1
0
0
0
X
X
X
X
X
X
z
1
0
1
0
1
0
1
0
1
0
X
X
X
X
X
X
Nullstellenmenge von w
Einsstellenmenge von w
Don't care-Menge (DC) von w
Diese Eingangsbelegungen sollten in
der Praxis nicht auftreten, der
zugehörige Ausgangswert ist „don‘t care“.
Folie 8-57
Unvollständig spezifizierte Funktionen
Optimierung von
Schaltnetzen
Wie berücksichtigt man die DC-Menge bei der zweistufigen Minimierung?
DCs können wie 0 oder 1 behandelt werden, je nachdem was vorteilhafter ist
⇒ bei der Berechnung von Primimplikanten: behandle DCs wie Einsstellen,
dadurch entstehen mehr Möglichkeiten zur Überdeckung der "echten" Einsstellen
⇒ bei der Lösung des Überdeckungsproblems: behandle DCs wie Nullstellen
Beispiel:
Kurzschreibweise für DC-Minterme
ƒ(a, b, c, d) = Σm(4, 5, 6, 8, 9, 10, 13) + Σd(0, 7, 15)
wird bei der Berechnung der Primimplikanten behandelt wie
ƒ(a, b ,c ,d) = Σm(0, 4, 5, 6, 7, 8, 9, 10, 13, 15)
wird bei der Lösung des Überdeckungsproblems behandelt wie
ƒ(a, b, c, d) = Σm(4, 5, 6, 8, 9, 10, 13)
vgl. Beispiel zur QuineMcCluskey-Methode!
Folie 8-58
Optimierung von
Schaltnetzen
Zweistufige Minimierung mit DCs
Entwurfsbeispiel: BCD-Inkrementierer
a
ab
00
01
11
10
00
0
0
X
1
01
0
0
X
0
cd
w
a
ab
d
11
0
1
X
X
10
0
0
X
X
00
01
11
10
00
0
1
X
0
01
0
1
X
0
cd
x
c
d
11
1
0
X
X
10
0
1
X
X
c
b
b
a
ab
00
01
11
10
00
0
0
X
0
01
1
1
X
0
cd
y
a
ab
d
11
0
0
X
X
10
1
1
X
X
c
00
01
11
10
00
1
1
X
1
01
0
0
X
0
cd
z
d
11
0
0
X
X
10
1
1
X
X
c
b
b
Folie 8-59
Optimierung von
Schaltnetzen
Zweistufige Minimierung mit DCs
a
ab
00
01
11
10
00
0
0
X
1
01
0
0
X
0
cd
w
a
ab
d
11
0
1
X
X
10
0
0
X
X
00
01
11
10
00
0
1
X
0
01
0
1
X
0
cd
x
c
d
11
1
0
X
X
10
0
1
X
X
c
b
b
a
ab
00
01
11
10
00
0
0
X
0
01
1
1
X
0
cd
y
a
ab
d
11
0
0
X
X
10
1
1
X
X
c
00
01
11
10
00
1
1
X
1
01
0
0
X
0
cd
z
d
11
0
0
X
X
10
1
1
X
X
c
b
w = bcd + ad'
x = bc' + bd' + b'cd
b
y = a'c'd + cd'
z = d'
Folie 8-60
Heuristiken
Optimierung von
Schaltnetzen
Viele Minimierungsprobleme lassen sich in der Praxis aufgrund zu hohen
Rechenaufwands nicht exakt lösen.
Es werden deshalb Verfahren verwendet, die auf den Anspruch verzichten, stets die
optimale Lösung zu finden. Dafür können solche Verfahren aber wesentlich
schneller sein. Durch geschicktes Raten oder durch eine aus der Anschauung
begründbare Strategie werden Lösungen ermittelt, die dem Optimum möglichst
nahe sind. Solche Ratestrategien werden auch als "Heuristiken" bezeichnet.
Heuristiken können auch innerhalb eines exakten Verfahrens angewendet werden,
um die theoretische worst-case-Komplexität des Verfahrens so oft wie möglich zu
vermeiden.
Beispiel: Mengenüberdeckungsproblem
Zur Bestimmung der minimalen Überdeckung wähle immer die größte noch
verfügbare Teilmenge aus.
"Greedy-Heuristik" (engl. greedy: gierig, gefräßig, habgierig)
Folie 8-61
CAD-Werkzeuge für
die zweistufige Minimierung
Optimierung von
Schaltnetzen
ESPRESSO-Methode
Problem bei Quine-McCluskey: Komplexität
• Anzahl der Primimplikanten kann exponentiell mit Anzahl der
Eingangsvariablen wachsen.
• Rechenaufwand zur Lösung des Überdeckungsproblems kann exponentiell
mit der Größe der Überdeckungsmatrix wachsen.
ESPRESSO: höhere Rechengeschwindigkeit, aber nur heuristische
(näherungsweise) Lösung
• generiert nicht alle Primimplikanten
• wählt eine Hülle (Menge von Implikanten, die alle Einsstellen überdecken)
als Ausgangsbasis
• löst Überdeckungsproblem durch lokale Modifikationen der Hülle
Folie 8-62
CAD-Werkzeuge für
die zweistufige Minimierung
Optimierung von
Schaltnetzen
Public domain Werkzeug ESPRESSO: Eingabe und Ausgabe
ƒ(A,B,C,D) = ∑ m(4,5,6,8,9,10,13) + d(0,7,15)
Eingabe für ESPRESSO
.i 4
.o 1
.ilb a b c d
.ob f
.p 10
0100 1
0101 1
0110 1
1000 1
1001 1
1010 1
1101 1
0000 0111 1111 .e
-- # inputs
-- # outputs
-- input names
-- output name
-- number of product terms
-- a'bc'd'
-- a'bc'd
-- a'bcd'
-- ab'c'd'
-- ab'c'd
-- ab'cd'
-- abc'd
-- a'b'c'd' don't care
-- a'bcd don't care
-- abcd don't care
-- end of list
Ausgabe von ESPRESSO
.i 4
.o 1
.ilb a b c d
.ob f
.p 3
1-01 1
10-0 1
01-- 1
.e
ƒ = ac'd + ab'd' + a'b
Folie 8-63
Optimierung von
Schaltnetzen
ESPRESSO
Beispiel: lokale Modifikation der Hülle
a
ab
00
01
11
10
00
1
1
0
0
01
1
1
1
1
cd
a
ab
00
01
11
10
00
1
1
0
0
01
1
1
1
1
cd
d
11
0
0
1
d
1
c
11
0
0
1
1
10
1
1
1
1
c
10
1
1
1
1
b
Ausgangssituation
4 Primimplikanten, keine
redundanten Terme!
(Hülle ist „prim“ und „irredundant“)
b
„reduziere“
Implikanten
(aber so, dass immer noch
alle Einsstellen überdeckt sind)
Folie 8-64
Optimierung von
Schaltnetzen
ESPRESSO
Beispiel (Forts.): lokale Modifikation der Hülle
a
ab
00
01
11
10
00
1
1
0
0
01
1
1
1
1
cd
a
ab
00
01
11
10
00
1
1
0
0
01
1
1
1
1
cd
d
11
0
0
1
d
1
c
11
0
0
1
1
10
1
1
1
1
c
10
1
1
1
b
„Expandiere“ zu (anderen)
Primimplikanten
1
b
Ein Primimplikant wird redundant
und kann aus der Hülle entfernt
werden.
jetzt nur 3 Primimplikanten!
Folie 8-65
Optimierung von
Schaltnetzen
ESPRESSO
ESSPRESSO-Heuristik
Try-and-Error-Methode:
- reduziere Würfel (beseitige Überlappungen)
- expandiere Würfel (möglichst in eine andere Richtung
als die, aus der vorher reduziert wurde)
- entferne redundante Würfel
wiederhole diesen Vorgang viele Male,
behalte die beste erzeugte Lösung
Wie überprüft man, ob ein Würfel in eine bestimmte Richtung reduziert bzw.
expandiert werden kann? Abbildung auf Tautologieproblem! (Dualfall des SATProblems).
Innerhalb von ESPRESSO wird also viele Male das Tautologieproblem gelöst.
Folie 8-66
Mehrstufige Schaltungen
Optimierung von
Schaltnetzen
Zweistufige Schaltungen bestehen aus zwei Gatterebenen,
z.B.: AND-OR, OR-AND, NAND-NAND, NOR-NOR
In mehrstufigen Schaltungen bestehen keine (prinzipiellen)
Einschränkungen hinsichtlich
- Zahl der Gatterebenen
- Wahl der Gattertypen
⇒ die bisher betrachteten Entwurfs- und Optimierungsverfahren sind für
mehrstufige Schaltungen nicht ausreichend
Folie 8-67
Optimierung von
Schaltnetzen
Mehrstufige Schaltlogik
optimierter SOP-Ausdruck:
x = adf + aef + bdf + bef + cdf + cef + g
6 x 3-fach AND-Gatter, 1 x 7-fach OR-Gatter (zu hoher Fanin!)
25 Leitungen (19 Literale und 6 interne Verbindungen)
a
d
f
a
e
f
b
d
f
b
e
f
c
d
f
c
e
f
g
1
2
a
b
c
1
3
d
e
2
7
4
5
6
x
3
4
x
f
g
faktorisierter Ausdruck:
x = (a + b + c) (d + e)f + g
1 x 3-fach OR-Gatter, 2 x 2-fach OR Gatter,
1 x 3-fach AND-Gatter
10 Leitungen (7 Literale plus 3 interne Verbindungen)
Folie 8-68
Mehrstufige Schaltlogik
Optimierung von
Schaltnetzen
Optimierung mehrstufiger Schaltungen
Optimierungsziel: mehrstufige Gatternetzliste mit möglichst wenig Gattern und
möglichst kleinen Fanins.
Im Unterschied zum zweistufigen Fall existiert bei mehrstufigen Schaltungen keine
einheitliche Sichtweise auf das Optimierungsproblem. Es kommt eine Vielfalt von
Heuristiken zum Einsatz. Ziel ist es meist "geschickte" Faktorisierungen zu finden,
die zu kompakten Ausdrücken führen. Außerdem sollen möglichst große
Teilausdrücke für mehrere Schaltungsausgänge gleichzeitig verwendet werden.
Manche Algorithmen führen die Faktorisierung auf ein Minimierungsproblem für
zweistufige Schaltungen zurück.
Folie 8-69
Optimierung von
Schaltnetzen
Mehrstufige Schaltlogik
Optimierung:
Minimiere Anzahl der Literale (technologieunabhängig):
faktorisiere so aus, dass Gatter und Verbindungen eingespart werden und dass
Schaltlogik mehrfach benutzt werden kann, beachte zeitliche Anforderungen
(Faktorisierung reduziert meist Fanin, erhöht aber Anzahl der Schaltungsebenen)
Faktorisierte Form:
Summe von Produkten von Summen von Produkten . . .
a
•
b
b'
+
x = (ab + b'c) (c + d(e + ac')) + (d + e)(fg)
•
c
a
•
c'
y = (d + e)(fg) + h
+ f3
•
f1
f
+
g
d
e
h
•
c
d
e
faktorisierte Form:
f2
+
f4
•
x
f6 = (d + e)(fg)
• f6
+f
5
gemeinsam nutzbare Schaltlogik:
+
y
Folie 8-70
Verknüpfungsbasen
Optimierung von
Schaltnetzen
Wahl von Gattertypen zur Implementierung
Nach dem Hauptsatz der Schaltalgebra läßt sich jede beliebige Schaltfunktion
durch die drei Grundverknüpfungen {AND, OR, NOT} eindeutig darstellen.
{AND, OR, NOT} ist eine Verknüpfungsbasis oder ein Basissystem der
zweiwertigen Booleschen Algebra.
weitere wichtige Basissysteme (siehe Anhang A):
{NAND}, {NOR}, {AND, NOT}, {OR, NOT}, {AND, XOR, 1}
Eine Gatterbibliothek, die als Grundlage für die Schaltungsimplementierung
dienen soll, muss mindestens eines dieser Basissysteme enthalten.
Die Basissysteme {NAND} und {NOR} sind aus technischen Gründen (siehe
Kap. 7) besonders wichtig!
Folie 8-71
Optimierung von
Schaltnetzen
Wahl des Gattertypen
NAND- und NOR-Netzwerke
DeMorgan's Gesetz:
(a + b)' = a'·b'
(a·b)' = a' + b'
andere Schreibweise: a + b = (a' · b')'
(a·b) = (a' + b')'
"Bubble" bedeutet Negation
OR/NAND-Äquivalenz
a
0
0
1
1
a b b
1 0 1
1 1 0
0 0 1
0 1 0
a +b
0
1
1
1
a· b
0
1
1
1
a +b
1
1
1
0
a · b
1
1
1
0
a
b
= a
a
b
=
b
a
b
Folie 8-72
Optimierung von
Schaltnetzen
Wahl des Gattertypen
AND/NOR-Äquivalenz
a
0
0
1
1
a b b
1 0 1
1 1 0
0 0 1
0 1 0
a · b
0
0
0
1
a+b
0
0
0
1
a · b
1
0
0
0
a +b
1
0
0
0
a
b
=
a
b
a
b
=
a
b
Netzwerke
Netzwerkebestehend
bestehendaus
ausANDs
ANDsund
undORs
ORs
können
könnenalso
alsodurch
durchEinfügen
Einfügengeeigneter
geeigneterInverter
InverterininNetzwerke,
Netzwerke,
die
diejeweils
jeweilsnur
nuraus
ausNANDs
NANDsoder
oderNORs
NORsbestehen,
bestehen,umgewandelt
umgewandelt
werden.
(Manuelles
Verfahren:
"Bubble-Methode")
werden. (Manuelles Verfahren: "Bubble-Methode")
Folie 8-73
Optimierung von
Schaltnetzen
Wahl des Gattertypen
Beispiel: bilde AND/OR-Netzwerk auf NAND/NAND-Netzwerk ab
NAND
a
a
b
b
z
c
d
NAND
z
NAND
c
d
Eine DNF kann also durch NAND-Gatter implementiert werden, indem im
zugehörigen AND/OR-Netzwerk alle Gatter durch NAND-Gatter ersetzt werden.
dualer Fall:
KNF lässt sich unmittelbar durch NOR-Gatter implementieren, indem
alle Gatter durch NOR-Gatter ersetzt werden
Folie 8-74
Optimierung von
Schaltnetzen
Mehrstufige Schaltlogik
Beispiel
f = a(b + cd) + bc'
ursprüngliches
AND-OR-Netzwerk
Einfügen von 2 Invertern
vor OR-Gattern,
1 Inverter wird
zurückgeschoben
mit NAND-Gattern
neuzeichnen
Einfügen von 2 Invertern vor ORGattern → NAND-Netzwerk
Ebene 1
c
d
b
a
b
c'
c
d
b
a
b
c'
c
d
b'
a
b
c'
G1
Ebene 2
Ebene 3
Ebene 4
G3
G4
G5
f
G4
G5
f
G2
G1
G3
G2
G1
G3
G4
G5
G2
Folie 8-75
f
Mehrstufige Schaltlogik: mehr als zwei Ebenen
Optimierung von
Schaltnetzen
noch ein Beispiel: Umwandlung in NAND-Netzwerk
a
b
c
a
f
x
b
c
f
x
d
d
(a) ursprüngliche Schaltung
(b) einfügen von Doppelinvertern
a
x
a
b
c
f
x'
d'
(c)
b
c
f
x'
d'
verteile Inverter,
Konflikte möglich
(d) füge Inverter ein, um Konflikte
zu lösen
Folie 8-76
Wahl des Gattertypen
Optimierung von
Schaltnetzen
Die Wahl der Gattertypen in einer kombinatorischen Schaltung hat großen Einfluss
auf die Qualität der Implementierung. Es sind unterschiedliche Bausteine zur
Implementierung verschiedener Gatterfunktionen im Handel erhältlich.
Für den Entwurf integrierter mikroelektronischer Schaltungen stellen die Hersteller
unterschiedliche "Zellen" (= Gatter) zur Verfügung, deren Implementierungskosten
hinsichtlich Fläche und Signallaufzeiten bekannt sind. Die von einem Halbleiterhersteller unterstützten Zellen werden in einer Zellbibliothek zusammengefasst und
von den CAD-Werkzeugen berücksichtigt.
Für ein und denselben Gattertyp (z.B. Inverter) können mehrere Varianten zur
Verfügung stehen. Auf dem kritischen Pfad verwendet man Zellen, die möglichst
schnell sind, dafür aber mehr Fläche benötigen, abseits des längsten (kritischen)
Pfads können langsamere und kleinere Gatter zum Einsatz kommen.
Neben AND, OR, NOT, NAND, NOR, XOR, XNOR gibt es weitere Gatterbausteine, die komplexere Funktionen implementieren, sog. Komplexgatter.
Eine (möglichst) optimale Überdeckung der Schaltung durch die verfügbaren Zellen
einer Bibliothek zu bestimmen, ist Aufgabe des technology mappings.
Folie 8-77
Logiksynthese
Optimierung von
Schaltnetzen
"Logiksynthese":
Schritt 1: technologieunabhängige Optimierung (minimiere Anzahl der Literale)
Schritt 2: technology mapping (Wahl der Gattertypen)
Public Domain Synthesetool SIS (enthält auch ESPRESSO):
Die in SIS implementierten Algorithmen sind Kern weit verbreiteter kommerzieller
Synthesewerkzeuge (z.B. SYNOPSYS).
Datei beschreibt Volladdierer:
INORDER = a b ci;
OUTORDER = co sum;
co = a*b*ci + a*b!ci + a*!b*ci + !a*b*ci;
sum = a*b*ci + a*!b*!ci + !a*b*!ci + !a*!b*ci;
Folie 8-78
Logiksynthese
Optimierung von
Schaltnetzen
Beispiel: Optimierung eines Volladdierers mit SIS
% sis
UC Berkeley, SIS 1.3 (compiled Tue Apr 7 14:35:02 MET DST 1998)
sis> re full.adder
sis> p
"read equations"
{co} = a b ci + a b ci' + a b' ci + a' b ci
{sum} = a b ci + a b' ci' + a' b ci' + a' b' ci
sis> pf
{co} = a b' ci + b (ci (a' + a) + a ci')
{sum} = ci (a' b' + a b) + ci' (a b' + a' b)
zweistufige Minimierung
sis> sim1 *
("simplify")
sis> p
{co} = a b + a ci + b ci
{sum} = a b ci + a b' ci' + a' b ci' + a' b' ci
sis> pf
{co} = ci (b + a) + a b
{sum} = ci (a' b' + a b) + ci' (a b' + a' b)
sis> gd *
sis> pf
"good decomposition"
{co} = a [2] + b ci
{sum} = a' [3]' + a [3]
[2] = ci + b
[3] = b' ci' + b ci
bis jetzt technologieunabhängig!
Folie 8-79
Logiksynthese
sis> rlib msu.genlib
sis> map
sis> pf
[361] = b' ci' + a'
[328] = b'
[329] = ci'
{co} = [328]' [329]' + [361]'
[3] = b ci' + b' ci
{sum} = [3] a' + [3]' a
sis> pg
[361]
1890:physical 32.00
[328]
1310:physical 16.00
[329]
1310:physical 16.00
{co}
1890:physical 32.00
[3]
2310:physical 40.00
{sum} 2310:physical 40.00
sis> pat
... using library delay model
{sum} : arrival=( 2.2 2.2)
{co}
: arrival=( 2.2 2.2)
[328] : arrival=( 1.2 1.2)
[361] : arrival=( 1.2 1.2)
[329] : arrival=( 1.2 1.2)
[3]
: arrival=( 1.2 1.2)
ci
: arrival=( 0.0 0.0)
b
: arrival=( 0.0 0.0)
a
: arrival=( 0.0 0.0)
sis> quit
%
Optimierung von
Schaltnetzen
lese Gatterbibliothek ein und
führe Technologieabbildung durch
Gatter zur Implementierung
der verschiedenen Knoten
und ihr Flächenbedarf
Angabe des Zeitverhaltens
Einheitsverzögerung plus 0.2
Zeiteinheiten pro Nachfolgeknoten
("print arrival times")
Folie 8-80
Optimierung von
Schaltnetzen
Logiksynthese
Ergebnis der Optimierung mit SIS:
(VLSI Standardzellen-Entwurf)
[3]
b
ci
sum
2310
a
2310
a
b
ci
+
[361]
&
&
1890
[328]
+
co
1890
b
1310
[329]
ci
1310
Beachte: OR-AND-INVERT
äquivalent zu INVERT-AND-OR
Zellbibliothek ("msu.genlib")
Nummer Name
1310
inv
Funktion
A'
1120
1130
1140
nor2
nor3
nor4
(A+B)'
(A+B+C)'
(A+B+C+D)'
1220
1230
1240
nand2
nand3
nand4
(A• B)'
(A• B• C)'
(A• B• C• D)'
1660 and2/nand2 [A• B, (A• B)']
1670 and3/nand3 [A• B• C, (A• B• C)']
1680 and4/nand4 [A• B• C• D, (A• B• C• D)']
1760 or2/nor2
1770 or3/nor3
1780 or4
[A+B, (A+B)']
[A+B+C, (A+B+C)']
(A+B+C+D)
1870
1880
1860
1890
aoi22
aoi21
oai22
oai21
(A• B + C• D)'
(A + B• C)'
[(A + B)(C + D)]'
[A (B + C)]'
1970
1810
1910
1930
ao22
ao222
ao2222
ao33
A•
A•
A•
A•
2310 xor2
2350 xnor2
B + D• E
B + C• D + E• F
B + C• D + E• F + G• H
B• C + D• E• F
A• B' + A'• B
A• B + A'• B'
Folie 8-81
Technische Informatik I
Kapitel 9
Bausteine digitaler Entwürfe
Folie 9-1
Bausteine digitaler Entwürfe
Vorbemerkung
In diesem Kapitel betrachten wir Bausteine für den Entwurf digitaler
Schaltungen. Wir beschränken uns auf Bausteine, die kombinatorische
Schaltungen implementieren. Größere Funktionseinheiten mit
sequentiellem Verhalten sind Gegenstand von Kap. 12.
Bereits betrachtet wurden Gatter: AND, NAND, OR, NOT, NOR, XOR,
XNOR, AOI
Thema dieses Kapitels:
• programmable logic devices (PLD): PLA und PAL
• spezielle Logikbausteine:
Multiplexer und Dekoder,
tri-state-Gatter,
ROM (read only memory)
Folie 9-2
Bausteine digitaler Entwürfe
PALs und PLAs
Programmable Array Logic (PAL) und Programmable Logic Array (PLA)
Vorgefertigte Bausteine bestehend aus vielen AND/OR-Gattern (oder NOR, NAND),
"personalisierbar“ durch das Herstellen oder Löschen von Verbindungen
Eingänge
Feld von AND-Gattern
Produktterme
Feld von OR-Gattern
Ausgänge
Blockdiagramm: programmierbare Felder für SOP-Ausdrücke
Folie 9-3
Bausteine digitaler Entwürfe
PALs und PLAs
Unterschied zwischen Programmable Array Logic (PAL) und
Programmable Logic Array (PLA)
PAL-Konzept:
eingeschränkte Topologie des OR-Feldes,
AND-Feld programmierbar, OR-Feld fest verdrahtet
Jede Spalte im OR-Feld hat nur
zu einer eingeschränkten Menge
von Produkttermen Zugang
PLA-Konzept: AND- und OR-Ebene sind programmierbar
aber: programmierbare Verbindungen ( ) sind langsamer als fest
verdrahtete ( )
Folie 9-4
Bausteine digitaler Entwürfe
PALs und PLAs
Personalisierungsmatrix
Beispiel
Gleichungen
f0 = a + b'c'
f1 = ac' + ab
f2 = b'c' + ab
f3 = b'c + a
mehrfach
genutzte
Terme
Eingänge
ab
1
1 -
Ausgänge
f 1 f2
0
1
1
bc
-
0 1
0
0
0
1
ac
1
- 0
0
1
0
0
bc
-
0 0
1
0
1
0
a
1
-
-
1
0
0
1
Produktterme
a b c
f0
f3
0
Eingangsseite:
1 = tritt im Term unkomplementiert auf
0 = tritt im Term komplementiert auf
- = tritt im Term nicht auf
Ausgangsseite:
1 = Term tritt in Summe auf
0 = Term tritt in Summe nicht auf
Folie 9-5
Bausteine digitaler Entwürfe
PALs und PLAs
Beispiel (Forts.)
a b
c
Vor der Programmierung sind alle
denkbaren Verbindungen hergestellt
f0
f1
f2
f3
Folie 9-6
Bausteine digitaler Entwürfe
PALs und PLAs
Beispiel (Forts.)
a
b
c
Unerwünschte Verbindungen werden gelöscht
(mittels eines Programmiergerätes werden Sicherungen
durchgebrannt)
ab
b'c
ac'
b'c'
a
Beachte:
es gibt auch programmierbare Felder,
bei denen Verbindungen nicht gelöscht,
sondern hergestellt werden.
f0
f1
f2
f3
Folie 9-7
Bausteine digitaler Entwürfe
PALs und PLAs
Alternative Darstellung für Strukturen mit hohem Fanin
nicht alle Verbindungsdrähte
müssen gezeichnet werden
a
b
c
d
ab
a'b'
cd'
Implementierung von:
f0 = ab + a'b'
f1 = cd' + c'd
c'd
ab + a'b' cd' + c'd
Folie 9-8
Bausteine digitaler Entwürfe
PALs und PLAs
Entwurfsbeispiel
a
b
c
abc
Funktionsgenerator für AND, OR,
NAND, NOR, XOR, XNOR
mit 3 Eingängen
a
b
c
a
b
Schaltung mit mehreren Ausgängen
c
f1 = abc
abc
f2 = a + b + c
abc
abc
f3 = abc
abc
f4 = a + b + c
abc
abc
f5 = a xor b xor c
abc
f6 = a xnor b xnor c
f1
f2
f3
f4
f5
Folie 9-9
f6
Bausteine digitaler Entwürfe
PALs und PLAs
Entwurfsbeispiel
BCD → Gray-Code Konvertierung einer Dezimalziffer
a
ab
a
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
b
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
c
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
d
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
w
0
0
0
0
0
1
1
1
1
1
X
X
X
X
X
X
x
0
0
0
0
1
1
0
0
0
0
X
X
X
X
X
X
y
0
0
1
1
1
1
1
1
0
0
X
X
X
X
X
X
z
0
1
1
0
0
0
0
1
1
0
X
X
X
X
X
X
minimierte Funktionen:
w = a + bd + bc
x = bc'
y=b+c
z = a'b'c'd + bcd + ad' + b'cd'
00
01
11
10
00
0
0
X
1
01
0
1
X
1
11
0
1
X
X
cd
a
ab
00
01
11
10
00
0
1
X
0
01
0
1
X
0
11
0
0
X
X
10
0
0
X
X
cd
d
d
c
c
10
0
1
X
X
b
b
KV-Diagramm für w
a
ab
a
ab
00
01
11
10
00
0
1
X
0
01
0
1
X
0
11
1
1
X
X
cd
KV-Diagramm für x
00
01
11
10
00
0
0
X
1
01
1
0
X
0
11
0
1
X
X
10
1
0
X
X
cd
d
c
d
c
10
1
1
X
X
b
KV-Diagramm für y
b
KV-Diagramm für z
Folie 9-10
Bausteine digitaler Entwürfe
PALs und PLAs
a
b c
d
Realisierung durch PAL
4 Produktterme pro OR-Gatter
w
x
y
z
Folie 9-11
Bausteine digitaler Entwürfe
PALs und PLAs
Implementierung des Codewandlers aus einzelnen Gattern
a'
b
d
2
b
c
2
3
1
b
c'
2
x
b'
2
y
5 Standardbausteine statt 1
PLA/PAL Baustein!
w
a'
b'
c'
d
4
b
c
d
3
a
d'
5
b'
c
d'
3
4
Beispiel für kommerziell verfügbare
TTL-Standardbausteine:
1: TTL7404: 16 Inverter
2, 5: TTL7400: 4 2-fach NAND-Gatter
3: TTL7410: 3 3-fach NAND-Gatter
4: TTL7420: 2 4-fach NAND-Gatter
Folie 9-12
z
Bausteine digitaler Entwürfe
PALs und PLAs
Komparator für zwei 2-Bit-Zahlen
a
ab
01
11
10
00
1
0
0
0
01
0
1
0
0
00
01
11
10
00
0
1
1
1
01
1
0
1
1
cd
d
11
0
0
1
0
10
0
0
0
1
c
b
c
d
a
ab
00
cd
a
abcd
abcd
abcd
d
11
1
1
0
1
abcd
10
1
1
1
0
ac
c
b
KV-Diagramm für EQ
(ab = cd)
01
11
10
00
0
0
0
0
01
1
0
0
0
bd
00
01
11
10
00
0
1
1
1
01
0
0
1
1
cd
bd
a
ab
00
cd
KV-Diagramm für NE
(ab ≠ cd)
a
ab
ac
b
abd
bcd
d
11
1
1
0
1
c
abd
d
11
0
0
0
0
10
0
0
1
0
bcd
c
10
1
1
0
0
b
KV-Diagramm für LT
(ab < cd)
b
KV-Diagramm für GT
(ab > cd)
EQ NE LT
Folie 9-13
GT
Bausteine digitaler Entwürfe
FPGAs
Field programmable gate arrays
FPGAs sind programmierbare Bausteine, die auch die Implementierung
mehrstufiger Schaltungen erlauben.
I/O-Block
I/O-Block
I/O-Block
I/O-Block
I/O-Block
a
x
c
y
clock
I/O-Block
a
b
CLB
I/O-Block
a
b
c
I/O-Block
b
CLB
y
clock
d
x
c
CLB
y
clock
d
x
CLB (computational logic block):
implementiert "Teilschaltung" von
4-5 Variablen
d
Verdrahtungskanäle
a
b
c
CLB
I/O-Block
x
y
clock
Verdrahtungskanäle
I/O-Block
a
b
c
b
CLB
I/O-Block
x
y
d
c
x
y
d
Programmierung:
- CLBs mit Funktionen belegen
- Verbindungsstrukturen
personalisieren
a
b
CLB
CLB
a
b
clock
c
clock
d
a
I/O-Block
x
y
clock
d
c
a
b
CLB
x
y
clock
c
CLB
d
x
y
clock
d
(Beispiel: Xilinx XC2000 Serie)
Folie 9-14
Bausteine digitaler Entwürfe
Multiplexer/Demultiplexer
Multiplexer und Demultiplexer in digitalen Systemen
A
Demultiplexer
Y
Multiplexer
B
Z
A
Y
Demultiplexer
B
Multiplexer
Z
Mux/Demux können Verbindungen zwischen mehreren Punkten herstellen
Folie 9-15
Bausteine digitaler Entwürfe
Multiplexer/Demultiplexer
Verbindungen zwischen mehreren Punkten
a0
sa
a1
b0
b1
MUX
MUX
A
B
DEMUX
s0
sb
einer von mehreren Eingängen wird auf
einen Ausgang durchgeschaltet
Demultiplexer:
Sum
ss
Multiplexer:
ein Eingang wird auf einen von mehreren
Ausgängen durchgeschaltet
s1
Teilsystem für Addition:
z.B.: sa = 1, sb = 0, ss = 1
addiere a1 und b0 und gebe Ergebnis an s1
Folie 9-16
Bausteine digitaler Entwürfe
Multiplexer
allgemeines Konzept:
2n Dateneingänge, n Steuereingänge, 1 Ausgang
verbindet 2n Punkte mit einem einzigen Punkt,
Belegung des Steuersignals ist binärer Index des mit dem Ausgang
verbundenen Eingangs.
n = 1:
z = a'i0 + ai1
Zwei Darstellungen für eine 2:1 Mux
Wahrheitstabelle sind gebräuchlich.
a
0
1
z
i0
i1
i1
0
0
0
0
1
1
1
1
i0
0
0
1
1
0
0
1
1
a
0
1
0
1
0
1
0
1
Folie 9-17
z
0
0
1
0
0
1
1
1
Bausteine digitaler Entwürfe
Multiplexer
i0
i1
2:1
mux
z = a'i0 + ai1
z
a
i0
i1
i2
i3
4:1
mux
8:1
mux
i4
i5
i6
i7
z = a'b'i0 + a'bi1 + ab'i2 + abi3
b
a
i0
i1
i2
i3
z
z
z = a'b'c'i0 + a'b'ci1 + a'bc'i2 + a'bci3 +
ab'c'i4 + ab'ci5 + abc'i6 + abci7
2n -1
allgemein: z = Σ mkik
k=0
a
b
c
Mintermkurzschreibweise für 2n :1 Mux
Folie 9-18
Bausteine digitaler Entwürfe
Multiplexer
Kaskadierung von Multiplexern
i0
i1
i2
i3
0 4:1
1 mux
2
3s s
i4
i5
i6
i7
0 4:1
1 mux
2
3s s
1
1
b
Steuersignale b und c selektieren
gleichzeitig ein Signal aus i0-i3 und i4-i7
8:1
mux
0 2:1
mux
1 s
0
Steuersignal a entscheidet, welcher
Mux mit z verbunden wird
z
i0
0
i1
1 s
c
0
c
i2
0
i3
1 s
1
a
alternative Implementierung
eines 8:1 Mux
0
c
i4
0
i5
1 s
z
2
3 s0
a
c
i6
0
i7
1 s
c
Folie 9-19
s1
b
Bausteine digitaler Entwürfe
Multiplexer
Multiplexer als allgemeiner Logikbaustein
2n-1 : 1 Multiplexer kann jede Funktion aus n Variablen implementieren
n-1 Steuervariable, verbleibende Variable ist Dateneingang des Mux
Beispiel:
f(a, b, c) = m0 + m2 + m6 + m7
= a'b'c' + a'bc' + abc' + abc
= a'b'(c') + a'b(c') + ab'(0) + ab(1)
1
0
1
0
0
0
1
1
0
1
2
3
4
5
6
7
f
8:1
MUX
s2 s1 s0
a
b
c
a
0
0
0
0
1
1
1
1
b
0
0
1
1
0
0
1
1
c
0
1
0
1
0
1
0
1
f
1
0
1
0
0
0
1
1
c
c
0
1
c
c
0
1
0
1
2
3
4:1
MUX
s1
s0
a
"Lookup Table (LUT)"
(LUTs sind oft Bestandteil der CLBs eines FPGAs)
Folie 9-20
b
f
Bausteine digitaler Entwürfe
Dekoder/Demultiplexer
Dekoder (Demultiplexer): 1 Dateneingang, n Steuereingänge, 2n Ausgänge
Steuereingänge (bezeichnet mit „select“ oder „s“)
binärer Index des Ausgangs, auf den der Eingang durchgeschaltet wird
Dateneingang wird mit „enable“ oder „g“ bezeichnet
1:2 Dekoder:
o0 = g s'; o1 = g s
2:4 Dekoder:
o0 = g s0' s1'
3:8 Dekoder:
o0 = g s0' s1' s2'
o1 = g s0' s1' s2
o2 = g s0' s1 s2'
o1 = g s0' s1
o3 = g s0' s1 s2
o2 = g s0 s1'
o4 = g s0 s1' s2'
o3 = g s0 s1
o5 = g s0 s1' s2
o6 = g s0 s1 s2'
o7 = g s0 s1 s2
Folie 9-21
Bausteine digitaler Entwürfe
Dekoder/Demultiplexer
Dekoder als logisches Bauelement
g=d
3:8
dec
s2
a
s1
b
s0
0
1
2
3
4
5
6
7
abc
abc
abc
abc
abc
abc
abc
abc
Dekoder erzeugt geeignete
Minterme je nach Wahl der
Steuersignale
c
Beispiel:
f1 = a'bc'd + a'b'cd + abcd
f2 = abc'd' + abc
f3 = (abcd)'
Folie 9-22
Bausteine digitaler Entwürfe
Dekoder/Demultiplexer
Dekoder als logisches Bauelement (Beispiel)
4:16
dec
g
s 3 s 2 s 1 s0
a
b
c
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
a bcd
abcd
abcd
abcd
abcd
abcd
abcd
abcd
abcd
abcd
abcd
abcd
abcd
abcd
abcd
abcd
f1
f2
f3
d
Folie 9-23
Bausteine digitaler Entwürfe
Tri-State-Gatter
dritter Wert: "Z" — unendlicher Widerstand, keine Verbindung
Tri-State-Gatter: Ausgangssignale sind "0", "1", und "Z",
Eingangssignal a, zusätzlicher Eingang: output enable (oe)
f
a
oe
a
X
0
1
oe
0
1
1
f
Z
0
1
falls oe = 1, arbeitet Gatter wie ein Buffer (Signal wird elektrisch
verstärkt, bleibt logisch unverändert)
falls oe = 0, ist das Gatter vom Ausgang abgetrennt!
Es können also mehrere Gatter an die gleiche Leitung angeschlossen
werden, solange sichergestellt ist, dass nur für ein Gatter oe = 1 gilt
100
Signalverlauf
a
oe
f
"Z"
"Z"
Folie 9-24
Bausteine digitaler Entwürfe
Read-Only Memory (ROM)
ROM: zweidimensionales Feld von Nullen und Einsen
Zeile entspricht "Wort"; Index heißt "Adresse"
Zeilenbreite entspricht Bitbreite oder Wortbreite
Adresse ist Eingabe, ausgewähltes Wort ist Ausgabe
+5V +5V +5V +5V
n
2 -1
Dec
i
Wort 0011
j
Wort 1010
0
Bits
0
n-1
Adresse
Interner Aufbau
Folie 9-25
Bausteine digitaler Entwürfe
Read-Only Memory
Beispiel
f0 = a'b'c + ab'c' + ab'c
f1 = a'b'c + a'bc' + abc
f2 = a'b'c' + a'b'c + ab'c'
f3 = a'bc + ab'c' + abc'
Adresse
ROM
8 Worte mit je
4 Bits
a b c
Adresse
f0
f1
f2
a
b
c
f0
f
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
0
1
1
0
0
0
1
1
0
0
0
0
1
1
f2
f
1
1
0
0
1
0
0
0
0
0
0
1
1
0
1
0
3
Wortinhalte
f3
Ausgänge
Folie 9-26
Bausteine digitaler Entwürfe
Read-Only Memory
Ähnlich
Ähnlichwie
wiePLAPLAStruktur,
aber
Struktur, abermit
mit
Dekoder
als
Dekoder als
AND-Feld!
AND-Feld!
Speicherfeld
Dekoder
2n Wortzeilen
n Adressleitungen
2n Worte mit
m Bits
m Ausgänge
ROM vorteilhaft bei
(1) kurzen Entwurfszeiten (keine Minimierung der Funktionen nötig)
(2) Benutzung der meisten möglichen Eingangskombinationen (z.B. Codewandler)
Problem bei ROM: Größe verdoppelt sich für jeden zusätzlichen Eingang,
keine don‘t cares
PLA vorteilhaft wenn
(1) Optimierungswerkzeug wie ESPRESSO verfügbar ist
(2) relativ wenig unterschiedliche Minterme
(3) viele Minterme von Ausgängen gemeinsam genutzt werden
Folie 9-27
Bausteine digitaler Entwürfe
Kombinatorische Entwurfsaufgabe
Darstellung von BCD-Zahlen auf LCD-Anzeige mit 7 Segmenten
analysiere Problemstellung:
Eingabe: BCD-Zahl (4 Bit)
Ausgabe: Steuersignale für die Anzeige
4 Eingangssignale: a, b, c, d
LCD-Anzeige
(7 Segmente)
7 Ausgangssignale: c0 — c6
C0 C1 C2 C3 C4 C5 C6
C0
C5
C6
C4
C1
C2
Steuersignaldekoder
C3
C C C C C C C
0 1 2 3 4 5 6
Blockdiagramm
a
b
c
d
Folie 9-28
Bausteine digitaler Entwürfe
Kombinatorische Entwurfsaufgabe
LCD-Steuerung
a
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
b
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
c
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
d
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
c0
1
0
1
1
0
1
1
1
1
1
x
x
x
x
x
x
c1
1
1
1
1
1
0
0
1
1
1
x
x
x
x
x
x
c2
1
1
0
1
1
1
1
1
1
1
x
x
x
x
x
x
c3
1
0
1
1
0
1
1
0
1
0
x
x
x
x
x
x
c4
1
0
1
0
0
0
1
0
1
0
x
x
x
x
x
x
c5
1
0
0
0
1
1
1
0
1
1
x
x
x
x
x
x
c6
0
0
1
1
1
1
1
0
1
1
x
x
x
x
x
x
Formuliere Problem durch Wahrheitstabelle
Wähle Implementierungsstil:
falls ROM: fertig!
wegen don‘t cares ist aber PLA/PAL
attraktiv
Optimiere Entwurf:
Zweistufig:
manuell mit KV-Diagramm
oder
ESPRESSO
Mehrstufig:
SIS
Folie 9-29
Bausteine digitaler Entwürfe
Kombinatorische Entwurfsaufgabe
a
ab
00
01
11
10
00
1
0
X
1
01
0
1
X
1
11
1
1
X
X
ac
a
ab
00
01
11
10
00
1
1
X
1
01
1
0
X
1
11
1
1
X
X
cd
d
c
1
1
X
10
X
1
0
X
11
10
00
1
0
X
1
01
0
1
X
0
X
1
01
1
1
X
1
11
1
1
X
X
10
0
1
X
X
X
X
a
ab
01
11
10
00
1
0
X
1
01
0
0
X
0
00
01
11
10
00
1
1
X
1
01
0
1
X
1
cd
11
0
0
X
b
KV-Diagramm für C3
c0 = a + bd + c + b'd'
c1 = a + c'd' + cd + b'
c2 = a + b + c' + d
1
1
X
X
X
b
00
01
11
10
00
0
1
X
1
01
0
1
X
1
cd
d
d
11
0
0
X
X
11
1
0
X
X
10
1
1
X
X
c
c
10
a
ab
d
c
1
X
KV-Diagramm für C2
a
00
cd
X
c
1
1
d
X
d
10
1
b
ab
01
0
00
KV-Diagramm für C1
a
1
10
b
00
11
11
c
b
cd
01
d
KV-Diagramm für C0
ab
LCD-Steuerung
00
cd
c
10
a
ab
10
0
1
X
X
b
b
KV-Diagramm für C4
KV-Diagramm für C5
c3 = b'd' + cd' + bc'd + b'c
c4 = b'd' + cd'
c5 = a + c'd' + bd' + bc'
c6 = a + cd' + bc' + b'c
KV-Diagramm für C6
14 verschiedene
Produktterme!
Folie 9-30
Bausteine digitaler Entwürfe
Kombinatorische Entwurfsaufgabe
LCD-Steuerung
Increment
1
0
First
fuse
numbers
4
8
12
16
20
24
28
0
32
64
96
128
160
192
224
19
256
288
320
352
384
416
448
480
18
512
544
576
608
640
672
704
736
17
768
800
832
864
896
928
960
992
16
1024
1056
1088
1120
1152
1184
1216
1248
15
1280
1312
1344
1376
1408
1440
1472
1504
14
1536
1568
1600
1632
1664
1696
1728
1760
13
1792
1824
1856
1888
1920
1952
1984
2016
12
2
16H8PAL-Baustein
kann die Funktion
implementieren
3
4
5
6
7
8
9
11
Note: Fuse number = first fuse number + increment
Folie 9-31
Bausteine digitaler Entwürfe
Kombinatorische Entwurfsaufgabe
Increment
LCD-Steuerung
012 3
4
8
10
12
14
16
18
20
24
27
1
2
First
fuse
numbers
14H8PAL
kann die Funktion
nicht implementieren
23
0
28
56
84
22
1
112
140
21
168
196
20
224
252
19
280
308
18
336
364
17
392
420
16
448
476
504
532
15
3
4
5
6
7
8
9
10
14
11
13
Note: Fuse number = first fuse number + increment
Folie 9-32
Bausteine digitaler Entwürfe
Kombinatorische Entwurfsaufgabe
LCD-Steuerung
.i 4
.o 7
.ilb a b c d
.ob c0 c1 c2 c3 c4 c5 c6
.p 16
0000 1111110
0001 0110000
0010 1101101
0011 1111001
0100 0110011
0101 1011011
0110 1011111
0111 1110000
1000 1111111
1001 1110011
1010 ------1011 ------1100 ------1101 ------1110 ------1111 ------.e
Eingabe für
ESPRESSO
c0 = bc'd + cd + b'd' + bcd' + a
c1 = b'd + c'd' + cd + b'd'
c2 = b'd + bc'd + c'd' + cd + bcd'
c3 = bc'd + b'd + b'd' + bcd'
c4 = b'd' + bcd'
c5 = bc'd + c'd' + a + bcd'
c6 = b'c + bc' + bcd' + a
.i 4
.o 7
.ilb a b c d
.ob c0 c1 c2 c3 c4 c5 c6
.p 9
-10- 0000001
-01- 0001001
-0-1 0110000
-101 1011010
9 unterschiedliche Produktterme!
--00 0110010
--11 1110000
63 Literale, 20 Gatter
-0-0 1101100
1--- 1000011
Achtung:
-110 1011111
.e
In Kap. 8 wurde lediglich die exakte Optimierung für
Ausgabe von einstellige Funktionen (1 Ausgang!) betrachtet. Bei
mehrstelligen Funktionen müssen die Einsstellen aller
ESPRESSO
Ausgänge mit möglichst wenig Implikanten überdeckt
werden. Dies wird durch die Heuristiken in
ESPRESSO berücksichtigt. Deswegen liefert
ESPRESSO eine bessere Lösung als die exakte
Minimierung der einzelnen einstelligen
Funktionen.
Folie 9-33
Bausteine digitaler Entwürfe
Kombinatorische Entwurfsaufgabe
LCD-Steuerung
a
b c
d
bc'
b'c
b'd
bc'd
c'd'
cd
b'd'
a
bcd'
Implementierung mit PLA
C0 C1 C2
C3
C4 C5 C6
Folie 9-34
Bausteine digitaler Entwürfe
Kombinatorische Entwurfsaufgabe
LCD-Steuerung
x = c' + d'
y = b'c'
c0 = c3 + a'bx' + ady
52 Literale
33 Gatter
c1 = y + a'c5' + c'd'c6
c2 = c5 + a'b'd + a'cd
c3 = c4 + bdc5 + a'b'x'
mehrstufige Implementierung,
Optimierung mit SIS
c4 = d'y + a'cd'
c5 = c'c4 + ay + a'bx
c6 = ac4 + cc5 + c4'c5 + a'b'c
Folie 9-35
Technische Informatik I
Kapitel 10
Automaten als Verhaltensmodelle
sequenzieller Schaltungen
Folie 10-1
Automaten
Sequenzielle Schaltungen
Viele Schaltungen zeichnen sich dadurch aus, dass die Ausgabe der Schaltung nicht
nur von der aktuellen Eingabe, sondern auch von früheren Eingaben abhängt.
Solche Schaltungen lassen sich mathematisch nicht einfach durch eine Relation
oder Funktion modellieren; denn es werden nicht Elemente einer Menge auf
Elemente einer anderen oder der gleichen Menge abgebildet.
Häufig lässt sich dann jedoch das Schaltungsverhalten dadurch modellieren, dass
eine Folge (Sequenz) bestehend aus Elementen einer Menge auf eine Folge
(Sequenz) bestehend aus Elementen einer anderen oder der gleichen Menge
abgebildet wird. In diesem Fall spricht man von einer sequenziellen Schaltung.
Die Implementierung einer sequenziellen Schaltung erfordert die Möglichkeit,
frühere Eingaben (oder einen Zustand, der Informationen über frühere Eingaben
enthält) abzuspeichern.
Im Gegensatz dazu werden Schaltungen ohne Speicherfähigkeit, deren Ausgabe nur
von der aktuellen Eingabe abhängt, als kombinatorisch bezeichnet. Schaltnetze sind
kombinatorisch, und ihr mathematisches Modell sind (boolesche) Schaltfunktionen.
Folie 10-2
Automaten
Beispiel
Betrachtet wird ein Akkumulator. Der Akkumulator speichert intern ein Zahl. Zu
Beginn ist diese Zahl Null. Als Eingaben erhält er Zahlen aus N0 (Menge der
natürlichen Zahlen mit Null), die er zu der gespeicherten Zahl hinzuaddiert. Als
Ergebnis gibt er jeweils die gespeicherte Zahl aus.
x
akku= akku + x
y = akku
y
(x0, x1, x2, …) → (y0, y1, y2, …)
z.B.: (x0 = 3, x1 = 2, x2 = 4, x3 = 1, …) → (y0 = 0, y1 = 3, y2 = 5, y3 = 9, y4 = 10, …)
Folie 10-3
Automaten
Sequenzielle Schaltungen
Woraus resultiert das „Gedächtnis“ einer sequenziellen Schaltung?
y
x
z
b
a
„a hängt ab von b“
z+
Rückkopplung
Aus den Eingaben und dem aktuellen "Zustand" z wird ein nachfolgender Zustand z+
der Schaltung bestimmt. Die Ausgabe berechnet sich aus dem aktuellen Zustand
oder "Momentanzustand" und der Eingabe.
Beispiel (Forts.): der Zustand z ist durch den Inhalt des Akkus gegeben.
Folie 10-4
Automaten
Automaten
Sequenzielle Schaltungen können mathematisch durch Automaten modelliert werden.
Definition (Halbautomat, Medvedev-Automat)
Das Quadrupel M = (I, S, S0, δ) heißt deterministischer Halbautomat. Dabei
bezeichnet:
I eine Menge von erlaubten Eingabewerten
S eine Menge von Zuständen
S0 ⊆ S eine Menge von erlaubten Anfangszuständen
δ : S × I → S eine Übergangsfunktion.
Ist die Übergangsfunktion definiert als eine Abbildung δ : S × I → 2S , so heißt H
nicht-deterministischer Halbautomat. Ein Zustand kann also für ein und dieselbe
Eingabe mal in den einen, mal in den anderen Zustand aus einer Menge von
Zuständen übergehen.
Sind die Mengen S und S0 endlich, heißt H endlicher Halbautomat.
Folie 10-5
Automaten
Automaten
Erweitert man den Halbautomaten um eine Ausgabe, erhält man einen
(Voll)automaten. Dazu gibt es zwei Möglichkeiten:
Definition (Mealy-Automat)
Ein Mealy-Automat A = (I, O, S, S0, δ, λ) ist ein Halbautomat H erweitert um:
eine Menge O von Ausgabewerten
eine Ausgabefunktion λ : S × I → O.
Definition (Moore-Automat)
Ein Moore-Automat A = (I, O, S, S0, δ, λ) ist ein Halbautomat H erweitert um:
eine Menge O von Ausgabewerten
eine Ausgabefunktion λ : S → O.
Statt Mealy-Automat und Moore-Automat sagt man auch Mealy-„Maschine“
bzw. Moore-„Maschine“.
Folie 10-6
Automaten
Beispiel (Forts.)
x
y=z
z
z+ = z + x
y
y = λ(z) = z
z+ = δ (x , z) = x + z
z+
Die Ausgabe hängt nur vom Momentanzustand ab ⇒ Moore-Maschine
Wir wandeln den Akkumulator ab, so dass er als Ausgabe das Produkt aus der
aktuellen Eingabe und dem Akkuinhalt ausgibt.
x
y=z·x
z
z+ = z + x
y
z+
y = λ(z) = z · x
z+ = δ (x , z) = x + z
Die Ausgabe hängt vom Momentanzustand und der Eingabe ab ⇒ Mealy-Maschine
Folie 10-7
Automaten
Zustandsdiagramme
Endliche Automaten lassen sich durch „Zustandsgraphen“ oder
„Zustandsdiagramme“ darstellen:
• jeder Zustand entspricht einem Knoten des Graphen
• jede gerichtete Kante entspricht einem möglichen Zustandsübergang
Es ist üblich jeden Knoten mit dem zugehörigen Zustand zu beschriften. Bei
Moore-Automaten wird jede Kante mit der logischen Bedingung für den
Übergang und jeder Knoten mit der zugehörigen Ausgabe beschriftet. Bei
Mealy-Automaten wird jede Kante mit der zugehörigen logischen Bedingung
und der Ausgabe beschriftet.
Beispiel (Forts.)
S1= 5
[5]
S1= 5
3
3 / 15
S2= 8
[8]
S2= 8
zwei Zustände des Akkumulators (Moore)
zwei Zustände des abgewandelten
Akkumulators (Mealy)
Folie 10-8
Automaten
Beispiel
Getränkeautomat
Funktionsweise des Getränkeautomaten:
- Ausgabe einer Getränkedose nach Einwurf von 1,50 Euro
- Annahme von 50 Cent und 1 Euro Münzen
- kein Wechselgeld (Überzahlung wird aber akzeptiert)
- nur eine Getränkesorte
Folie 10-9
Automaten
Beispiel
Getränkeautomat
Münzerkenner
M
Steuerung
(Automat)
Reset
A
Mechanismus
zur Ausgabe einer
Getränkedose
Blockdiagramm
Mögliche Werte von Signal M: (Münzsorte)
0 (keine Münze eingeworfen)
C (50 Cent eingeworfen)
E (1 Euro eingeworfen)
Mögliche Werte von Signal A: (Ausgabe)
j (Ausgabe soll erfolgen)
n (Ausgabe soll nicht erfolgen)
Außerdem kann das Reset-Signal gesetzt werden, um den Automaten in
einen wohldefinierten Anfangszustand zu setzen.
Folie 10-10
Automaten
Beispiel
Getränkeautomat
Liste mögliche Eingabesequenzen auf:
3 × 50 Cent
1 Euro, 50 Cent
50 Cent, 1 Euro
1 Euro, 1 Euro
2 × 50 Cent, 1 Euro
Zeichne Zustandsdiagramm:
Eingangsignal M: 0, C, E
Ausgangssignal A: j, n
Konvention:
Reset-Zustand wird durch
Pfeil markiert
„0+C+E“: Signal ist 0
oder C oder E
Folie 10-11
Automaten
Beispiel
Getränkeautomat
Reset
Eigentlich müsste man
noch von jedem Knoten
eine Kante zum Anfangszustand zeichnen mit der
Übergangsbedingung, dass
das Reset-Signal gesetzt
ist. Dies lässt man aber zur
besseren Übersichtlichkeit
weg.
0
0+C+E C
0
S0
[n]
0
C
C
0
E
S1
S2
[n]
[n]
E 0+C+E 0+C+E C
E
0+C+E
S3
S4
S5
S6
[n]
[j]
[j]
[j]
E
0+C+E
S7
S8
[j]
[j]
Zustandsdiagramm (Moore)
für Getränkeautomat
(Annahme: der Ausgabemechanismus gibt eine weitere Dose erst aus, nachdem
A zwischenzeitig wieder den Wert n angenommen hat. Das Geld geht also
verloren. Der Automat ist erst nach einem Reset wieder funktionsfähig.)
Folie 10-12
Automaten
Beispiel
Getränkeautomat
Reset
Lasse zur besseren
Übersichtlichkeit die
Schlingen im
Zustandsdiagramm weg.
S0
[n]
C
C
C
E
S1
S2
[n]
[n]
E
C
E
S3
S4
S5
S6
[n]
[j]
[j]
[j]
E
S7
S8
[j]
[j]
Zustandsdiagramm (Moore) für
Getränkeautomat
Folie 10-13
Automaten
Beispiel
Getränkeautomat
Reset
Momentanzustand
0 Cent
[n]
Eingabe
M
Folgezustand
Ausgabe
A
0 Cent
0
C
E
0 Cent
50 Cent
1 Euro
n
n
n
50 Cent
0
C
E
50 Cent
1 Euro
1,5 Euro
n
n
n
1 Euro
0
C
E
1 Euro
1,5 Euro
1,5 Euro
n
n
n
1,5 Euro
0
C
E
1,5 Euro
1,5 Euro
1,5 Euro
j
j
j
C
50 Cent
[n]
E
C
1Euro
E
[n]
C+E
1,5 Euro
[j]
benutze Zustände
mehrfach
Zustandsdiagramm nach
Zustandsreduktion
("Schlingen" sind nicht gezeichnet)
Zustandstafel
Folie 10-14
Automaten
Äquivalente Automaten
Definition (Äquivalenz zweier Automaten)
Gegeben seien zwei deterministische Moore- oder zwei deterministische MealyAutomaten MA= (IA, OA, SA, S0,A, δA, λA) und MB = (IB, OB, SB, S0,B, δB, λB).
MA und MB befänden sich jeweils in einem ihrer Anfangszustände aus S0,A bzw.
S0,B.
MA und MB heißen äquivalent genau dann, wenn MA und MB für eine beliebige
Eingabefolge (x0, x1, x2, …), mit x0, x1, x2 … ∈ I und I = IA = IB, dieselbe
Ausgabefolge (y0, y1, y2, …), mit y0, y1, y2 … ∈ O und O = OA = OB erzeugen.
Beispiel:
Der Getränkeautomat nach der Zustandsreduktion ist zum ursprünglichen
Automaten äquivalent.
Folie 10-15
Automaten
Äquivalenz von Moore- und Mealy-Automat
Kann man einen Mealy-Automaten in einen Moore-Automaten umwandeln
und umgekehrt?
Ein/Ausgabeverhalten eines Moore-Automaten M:
x0, x1, x2,…
S0, S1, S2, S3,…
y0, y1, y2, y3,…
Ein-/Ausgabeverhalten eines Mealy-Automaten M´:
x0, x1, x2…
S0´, S1´, S2´, S3´,…
y1´, y2´, y3´,…
Das Ein-/Ausgabeverhalten kann nicht exakt das gleiche sein, da die Ausgabefolge
des Moore-Automaten ein Element mehr enthält, nämlich y0, die Ausgabe im
Anfangszustand. Ein Moore-Automat M und ein Mealy-Automat M´ werden als
äquivalent bezeichnet, wenn ausgehend von einem jeweiligen Anfangszustand S0
und S0´ für die gleiche Eingabefolge x0, x1, … gilt: yn = yn´ für alle n ≥ 1.
Folie 10-16
Automaten
Äquivalenz von Moore- und Mealy-Automat
Kann man einen Moore-Automaten in einen Mealy-Automaten umwandeln und
umgekehrt?
Moore nach Mealy:
Zu jedem Moore-Automaten M = (I, O, S, S0, δ, λ) gibt es einen äquivalenten
Mealy-Automaten, M´ = (I, O, S, S0, δ, λ´) mit
λ´ = λ (δ (x, z)), x ∈ I und z ∈S
A
x
B
A
x / yB
B
[yB]
[yA]
Moore
Mealy
Folie 10-17
Automaten
Beispiel
Getränkeautomat
Reset
Reset / n
0
0 Cent
MealyAutomat
0/n
MooreAutomat
0 Cent
[n]
0/n
C
0
50 Cent
C/n
50 Cent
E
E/n
[n]
C
C/n
1 Euro
E
[n]
1 Euro
0
C+E
E/j
0/n
C+E / j
1,5 Euro
1,5 Euro
[j]
0+C+E
Werte der Ausgangssignale sind mit
Zuständen assoziiert
0+C+E / j
Werte der Ausgangssignale sind mit
Übergängen assoziiert
Folie 10-18
Automaten
Äquivalenz von Moore- und Mealy-Automat
Mealy nach Moore:
Idee: jede Kombination aus momentaner Ausgabe und Nachfolgezustand der
Mealy-Maschine wird zu einem Nachfolgezustand der Moore-Maschine. Die
Ausgabe der Moore-Maschine gibt dann den Teil des Zustands aus, der der
Ausgabe der ursprünglichen Mealy-Maschine entspricht.
Also:
Zu jedem Mealy-Automaten M = (I, O, S, S0, δ, λ) gibt es einen äquivalenten
Moore-Automaten, M´ = (I, O, S´ = S × O, S0´ = S0 × O, δ´, λ´) und es gilt:
S´ ist die Menge aller Paare z´ = (z, y) mit z ∈ S und y = λ(x, z), x ∈ I.
δ´ setzt sich aus der Übergangsfunktion δ und der Ausgabefunktion λ des MealyAutomaten zusammen, δ´ = (δz´, δy´) = (δ (x, z), λ(x, z)).
λ´(z´) des Moore-Automaten gibt den „Teil“ des Zustands z´= (z, y) aus, der der
Ausgabe der Mealy-Maschine entspricht, d.h. λ´(z´) = y.
Folie 10-19
Automaten
Äquivalenz von Moore- und Mealy-Automat
Mealy nach Moore
A
xA / yC
C
xB / yC´
Mealy
B
A
xA
(C, yC)
[yC]
[yA]
Moore
B
[yB]
xB
(C, yC´)
[yC´]
Folie 10-20
Automaten
Zustandsreduktion
Die Kosten für die Implementierung eines Automaten (z.B. Schaltwerk) hängen
stark von der Anzahl der Zustände des Automaten ab.
Problem ("Zustandsreduktion" oder "Zustandsminimierung")
Gegeben: Zustandsdiagramm oder Zustandstafel eines endlichen
deterministischen Automaten M
Gesucht: Zustandsdiagramm oder Zustandstafel eines zu M äquivalenten
Automaten mit einer minimalen Anzahl von Zuständen
•
•
entwerfe Automaten zunächst, ohne auf Anzahl der Zustände Rücksicht zu
nehmen
führe anschließend Zustandsreduktion durch
Folie 10-21
Automaten
Beispiel
Automat zur Paritätsprüfung
0
[0]
1
S1
[1]
S0
S0, S2 sind äquivalente
Zustände:
S0
1
0
[0]
beide erzeugen Ausgangssignal 0
beide gehen bei Eingabe 1
nach S1 und bei Eingabe 0
zu sich selbst
0
1
0
S1
[1]
1
1
S2
[0]
unterschiedliche Zustandsdiagramme möglich:
0
• identisches Ausgangsverhalten für alle Eingangssequenzen
• Automaten sind äquivalent, erfordernaber unterschiedliche Implementierung
Folie 10-22
Automaten
Äquivalente Zustände
Definition (Äquivalente Zustände)
Zwei Zustände eines deterministischen Automaten heißen äquivalent genau dann,
wenn der mit diesen Zuständen initialisierte Automat in beiden Fällen für jede
mögliche Eingabesequenz die gleiche Ausgabesequenz erzeugt.
Satz
Zwei Zustände eines deterministischen Automaten sind äquivalent genau dann,
wenn für jede mögliche Eingabe die gleiche Ausgabe erzeugt wird und die
jeweiligen Nachfolgezustände äquivalent sind.
naheliegende Idee für Zustandsminimierung:
fasse äquivalente Zustände zu einem Zustand zusammen
Folie 10-23
Automaten
Zustandsreduktion
wie bestimmt man die Äquivalenzklassen?
(Vorläufiger) Algorithmus:
• stelle Zustandstafel auf
• identifiziere Zustände mit gleichen Ausgangssignalen
• gehen solche Zustände in die gleichenFolgezustände über, sind sie äquivalent
• fasse als äquivalent identifizierte Zustände zu einem einzigen Zustand (mit neuem
Namen) zusammen
• wiederhole diese Schritte, bis keine weiteren Zustände mehr zusammengefasst
werden können
Folie 10-24
Automaten
Beispiel
Zustandsreduktion durch Zeilenzusammenfassung in Zustandstafel
(vorläufiges Verfahren)
Automat zur Erkennung einer Zeichenkette:
Der Automat besitzt ein Eingangssignal x und ein Ausgangssignal y.
Er beobachtet die Eingabesequenz und betrachtet jeweils Gruppen von 4 Bits. Es
ist y = 1, falls die aktuelle Gruppe aus den Signalen 1010 oder 0110 besteht.
Beispiel für eine Eingangs-/Ausgangsfolge:
x = 0010
y = 0000
0110 1100 1010 0011
0001 0000 0001 0000
. . .
. . .
Anmerkung:
Automat identifiziert Zeichenkette ⇒ Automatentheorie spielt wichtige Rolle in
der Theorie formaler Sprachen!
Folie 10-25
Automaten
Beispiel
Zustandsreduktion durch Zeilenzusammenfassung in Zustandstafel
(vorläufiges Verfahren)
Reset
1/0
0/0
0/0
0/0
0/0
1/0
1/0 0/0
1/0
0/0
0/0
1/0
0/0
1/0
1/0
0/1
0/0
1/0
0/0 1/0
1/0
0/1
1/0
0/0
1/0
0/0 1/0
0/0
1/0
1/0
Folie 10-26
Automaten
Beispiel
Zustandsreduktion durch Zeilenzusammenfassung
(vorläufiges Verfahren)
Eingabefolge
Ausgabe
x =0 x =1
S0
S1
S1
S3
S2
S4
0
0
0
0
S2
S3
S5
S7
S6
S8
0
0
0
0
01
10
S4
S5
S9
S 11
S10
S12
0
0
0
0
11
000
S6
S7
S13
S0
S14
S0
0
0
0
0
001
010
011
S8
S9
S 10
S0
S0
S0
S0
S0
S0
0
0
1
0
0
0
100
101
S 11
S 12
S0
S0
S0
S0
0
1
0
0
110
111
S 13
S 14
S0
S0
S0
S0
0
0
0
0
Reset
0
1
00
Konfiguriere Zustandstafel
so, dass jede Eingabe für
Folgezustand und Ausgabe
jeweils einer Spalte
entspricht. Dadurch steht in
jeder Zeile für jeden
Momentanzustand, welche
Folgezustände und
Ausgaben möglich sind.
Momentanzustand
Folgezustand
x =0 x =1
Folie 10-27
Automaten
Beispiel
Zustandsreduktion durch Zeilenzusammenfassung
(vorläufiges Verfahren)
Eingabefolge
Momentanzustand
Folgezustand
x =0 x =1
Ausgabe
x =0 x =1
S0
S1
S1
S3
S2
S4
0
0
0
0
S2
S3
S5
S7
S6
S8
0
0
0
0
01
10
S4
S5
S9
S 11
S´10
S´10
0
0
0
0
11
000
S6
S7
S13
S0
S14
S0
0
0
0
0
001
010
S8
S9
S´10
S0
S0
S0
S0
S0
S0
0
0
1
0
0
0
S 11
S 13
S 14
S0
S0
S0
S0
S0
S0
0
0
0
0
0
0
Reset
0
1
00
011 oder 101
100
110
111
Folie 10-28
Automaten
Beispiel
Zustandsreduktion durch Zeilenzusammenfassung
(vorläufiges Verfahren)
Eingabefolge
Momentanzustand
Folgezustand
x =0 x =1
Ausgabe
x =0 x =1
S0
S1
S1
S3
S2
S4
0
0
0
0
S2
S3
S5
S´7
S6
S´7
0
0
0
0
01
10
S4
S5
S´7
S´7
S´10
0
0
11
S6
S´7
S´7
S0
S´10
S´7
S0
0
0
0
0
0
0
S´10
S0
S0
1
0
Reset
0
1
00
nicht 011 oder 101
011 oder 101
Folie 10-29
Automaten
Beispiel
Eingangsfolge
endgültige
endgültigereduzierte
reduzierte
Zustandstafel
Zustandstafel
Momentanzustand
S0
S1
S2
S3'
S4'
S7'
S10'
Reset
0
1
00 oder 11
01 oder 10
nicht (011 oder 101)
011 oder 101
Folgezustand
x=0 x=1
S1
S3'
S4'
S7'
S7'
S0
S0
S2
S4'
S3'
S7'
S10'
S0
S0
Ausgang
x=0 x=1
0
0
0
0
0
0
1
Reset
S0
0/0
S1
entsprechendes
entsprechendes
Zustandsdiagramm
Zustandsdiagramm
S2
1/0
0/0
1/0
0/0
1/0
S7'
0,1/0
0/0
S4'
S3'
0,1/0
1/0
S10'
0/1
1/0
Folie 10-30
0
0
0
0
0
0
0
Automaten
Zustandsreduktion
Zustandsreduktion durch Zeilenzusammenfassung
einfache Methode, aber:
liefert nicht immer die minimale Zustandstafel!
0
S0
[0]
Beispiel: Paritätsprüfer mit 3 Zuständen
Folgezustand
Momentanzustand x = 0 x = 1 Ausgabe
S
0
S0
S1
0
S1
S
1
S2
1
0
S
S2
S1
2
kann
kannSS00und
undSS22nicht
nichtzusammenfassen!
zusammenfassen!
1
0
S1
[1]
1
1
S2
[0]
0
Folie 10-31
Automaten
Zustandsreduktion
Zustandsreduktion durch Implikationstafel
neues Beispiel: Spezifikation eines Automaten
Eingangssignal x und Ausgangssignal y
Ausgangssignal ist 1, immer wenn eine Eingangsfolge 010 oder 110
an den Eingängen beobachtet wurde
Momentanzustand
Eingabefolge
Reset
0
1
00
01
10
11
S0
S1
S2
S3
S4
S5
S6
Folgezustand
x =0 x =1
S1
S3
S5
S0
S0
S0
S0
S2
S4
S6
S0
S0
S0
S0
Ausgabe
x =0 x =1
0
0
0
0
1
0
1
0
0
0
0
0
0
0
Folie 10-32
Automaten
Zustandsreduktion
Zustandsreduktion durch Implikationstafel
Enumeriere alle möglichen Zustandspaare und stelle die Bedingungen auf,
unter denen die Zustände eines Paares äquivalent sind
S0
In jedes Feld:
Trage für jede Eingabe
die Folgezustände für
das Zustandspaar ein.
Die Folgezustandspaare müssen äquivalent sein, damit das
Zustandspaar selbst
auch äquivalent ist.
S1
S1
S2
S2
S3
S3
S4
S4
S5
S5
S6
S6
S0
S1
S2
S3
S4
S5
S6
Äquivalenzrelation ist reflexiv und
symmetrisch:
kann Halbmatrix und Diagonale
weglassen
S0
S1
S2
S3
S4
Implikationstafel
Folie 10-33
S5
Automaten
Zustandsreduktion
Zustandsreduktion durch Implikationstafel
S1
S1-S3
S2-S4
S2
S1-S5 S3-S5
S2-S6 S4-S6
S3
S1-S0 S3-S0 S5-S0
S2-S0 S4-S0 S6-S0
S2 und S4 haben unterschiedliches Ein-/Ausgabeverhalten
Also können
S1 und S0 nicht
zusammengefaßt
werden
S4
S5
S6
S1-S0 S3-S0 S5-S0 S0-S0
S2-S0 S4-S0 S6-S0 S0-S0
S0-S0
S0-S0
S0 S1 S2 S3 S4 S5
anfängliche Implikationstafel
Folie 10-34
Automaten
Zustandsreduktion
Zustandsreduktion durch Implikationstafel
S1
Untersuche jedes Feld: streiche Zustandspaare, deren Äquivalenzbedingungen offensichtlich verletzt sind.
S2
Implikationstafel nach erstem Durchlauf
S4
zweiter Durchlauf bringt keine neue Information:
S5
S3
S3 und S5 sind äquivalent
S4 und S6 sind äquivalent
Also sind S1 und S2 auch äquivalent!
Eingangsfolge
reduzierte
reduzierte
Zustandstafel
Zustandstafel
Reset
0 oder 1
00 oder 10
01 oder 11
S3-S5
S4-S6
S0-S0
S0-S0
S0-S0
S0-S0
S6
S0
Momentanzustand
S0
S'1
S'3
S'4
S1
S2
Folgezustand
x =1
x =0
S'1
S'3
S0
S0
S3
S4
S5
Ausgabe
x =0 x =1
S'1
S'4
S0
S0
Folie 10-35
0
0
0
1
0
0
0
0
Automaten
Zustandsreduktion
Zustandsreduktion durch Implikationstafel
betrachte noch einmal Paritätsprüfer:
S1
S2
S0 – S2
S1 – S1
S0
S0 ist äquivalent zu S2,
da kein markiertes Zustandspaar
erreicht werden kann!
S1
Implikationstafel
Folie 10-36
Automaten
Zustandsreduktion
Zustandsreduktion durch Implikationstafel
Algorithmus
1. Stelle Implikationstafel auf.
2. Betrachte Feld für Si, Sj: falls Ausgänge unterschiedlich sind, markiere Feld
mit "X", sonst liste für alle Eingangskombinationen die implizierten
Folgezustandspaare auf.
3. Gehe von oben nach unten und links nach rechts durch die Implikationstafel:
falls ein Feld für Si, Sj das Folgezustandspaar Sm, Sn enthält und das Feld für
das Folgezustandspaar mit "X" markiert ist, dann markiere auch das Feld für
Si, Sj mit "X".
4. Wiederhole Schritt 3, bis keine neuen Felder mehr mit "X" markiert werden.
5. Jedes unmarkierte Feld gibt ein äquivalentes Zustandspaar an.
Folie 10-37
Automaten
Zustandsreduktion
Zustandsreduktion durch Implikationstafel
Ausfüllen der Implikationstafel:
•
Eintragxij — Zeile entspricht Si, Spalte entspricht Sj
•
Si ist äquivalent mit Sj, falls Ausgänge identisch und Folgezustände
äquivalent sind
•
xij enthält die Folgezustände von Si, Sj, die äquivalent sein müssen, damit Si
und Sj äquivalent sind
•
wennSi und Sj unterschiedliches Ausgangsverhalten haben, wird xij gestrichen
Beispiel:
S0 geht für 0 in S1 über, für 1 in S2
S1 geht für 0 in S3 über, für 1 in S4
also: Feld für S0 und S1 enthält Einträge:
S0
S1-S3
S2-S4
S1
S1-S3 (Übergang für 0)
S2-S4 (Übergang für 1)
Folie 10-38
Automaten
Zustandsreduktion
Gegeben sei ein endlicher deterministischer Automat M mit einer
Zustandsmenge S. Betrachte für die Zustände in S die Relation R "sind
äquivalent", d.h. R = {(Si, Sj) | Si und Sj sind äquivalent mit Si, Sj ∈ S}.
Welchen Typs ist R?
offensichtlich reflexiv, symmetrisch und transitiv
⇒ Äquivalenzrelation
Zustandsreduktion:
bestimme die Zerlegung (Partition) der Zustandsmenge in ihre
Äquivalenzklassen, jede Äquivalenzklasse ergibt einen Zustand im
reduzierten Automaten
Eine Zerlegung in Äquivalenzklassen ist eindeutig, das Zustandsdiagramm
des reduzierten Automaten ist daher eine eindeutige (kanonische)
Darstellung des Automaten. (Zustandsdiagramme sind isomorph.)
Folie 10-39
Technische Informatik I
Kapitel 11
Schaltwerke
Folie 11-1
Schaltwerke
Schaltwerke
Endliche Automaten dienen zur Modellierung von digitalen „sequenziellen
Schaltungen“ oder „Schaltwerken“.
Eine sequenzielle Schaltung mit n Eingangssignalen, m Ausgangssignalen und
k Zustandssignalen wird als endlicher Automat modelliert mit:
I ⊆ {0, 1}n als Menge der möglichen Eingaben
O ⊆ {0, 1}m als Menge der möglichen Ausgaben
S ⊆ {0, 1}k , S0 ⊆ S, als Zustands- und Anfangszustandsmenge
δ: S × I → S als Übergangsfunktion
λ : S → O (Moore) bzw. λ : S × I → O (Mealy) als Ausgabefunktion
Die Übergangs- und Ausgabefunktion sind offensichtlich Boolesche
Funktionen und können als kombinatorische Schaltung implementiert
werden.
Folie 11-2
Schaltwerke
Schaltung mit Rückkopplung
Wie implementiert man das Gedächtnis des Automaten in einem Schaltwerk?
x1
n („primäre“)
x2
Eingangssignale
xn
z1
z2
y1
y2
kombinatorische
Schaltung
implementiert δ und λ
zk
m („primäre“)
Ausgangssignale
ym
z1+
z2+
z k+
k Zustandssignale
Durch die Rückkopplung des Nachfolgezustandes auf den Momentanzustand wird
ein Gedächtnis implementiert. Die zeitlichen Abläufe in einem System mit
Rückkopplung sind jedoch schwer analysierbar und das Verhalten hängt stark von
den detaillierten Signallaufzeiten zur Berechnung der Nachfolgezustände ab.
Folie 11-3
Schaltwerke
Getaktete Schaltwerke
Wie implementiert man das Gedächtnis des Automaten in einem Schaltwerk?
x1
n („primäre“)
x2
Eingangssignale
xn
z1
z2
y1
y2
kombinatorische
Schaltung
implementiert δ und λ
zk
m („primäre“)
Ausgangssignale
ym
z1+
z2+
z k+
k Zustandssignale
Takt
getaktete "Binärspeicher", speichern
für jede Zustandsvariable den Wert 0
oder 1
Folie 11-4
Schaltwerke
Getaktete Schaltwerke
Getaktetes Schaltwerk: Übergangs- und Ausgabefunktion werten nur Eingaben
aus, die zu einem bestimmten Zeitpunkt, dem "Taktzeitpunkt" in einem
Binärspeicher abgespeichert wurden. Liegt der Taktzeitpunkt an jedem
Binärspeicher gleichzeitig an, dann heißt das Schaltwerk synchron.
In der Praxis entwirft man meist getaktete und synchrone Schaltwerke. Nichtsynchrone Signale werden durch Einfügen von getakteten Binärspeichern
synchronisiert.
Das Taktsignal (engl.: Clock) ist ein periodisches (oszillierendes) Signal. Das
„Taktereignis“ bestimmt, wann der Inhalt des Speichers durch den
Nachfolgezustand aktualisiert wird. Das Taktereignis kann in einer steigenden
oder fallenden Signalflanke oder in einem hohen oder niedrigen Signalpegel
bestehen.
Für die Realisierung der Binärspeicher gibt es verschiedene technische
Möglichkeiten: (flankengesteuerte) „Flipflops“ und (pegelgesteuerte) „Latches“
Folie 11-5
Schaltwerke
Flankengesteuertes D-Flipflop
Beispiel: flankengesteuertes D-Flipflop
Der Inhalt des Speichers wird bei steigender
Taktflanke mit dem Wert des Eingangs d
(Folgezustand) aktualisiert. Der Ausgang q gibt
den jeweils gespeicherten Wert
(Momentanzustand) aus.
D
Clk
(Takt)
Q
Schaltsymbol
Timing-Diagramm:
d
Clk
q
Folie 11-6
Schaltwerke
Beispiel
Ein endlicher Automat kann durch ein Schaltwerk implementiert werden, wenn man
den Elementen von I, O, S und S0 binäre Zahlen zuordnet. Diesen Vorgang nennt
man Kodierung.
Beispiel: Getränkeautomat
Kodierung der Eingabe: Die drei Werte 0, C, E des Signals m können durch eine
zweistellige binäre Zahl kodiert werden. Wir wählen:
0: 00
C: 01
E: 10
(11 wird nicht „gebraucht“!)
Kodierung der Ausgabe: Es genügt eine einstellige binäre Zahl. Wir wählen:
n: 0
j: 1
Kodierung der Zustände: Für die vier Zustände des reduzierten Automaten
benötigen wir zwei Zustandsbits.
0 Cent: 00
50 Cent: 01
1 Euro: 10
1,5 Euro: 11
Folie 11-7
Schaltwerke
Beispiel
Getränkeautomat
Schaltwerk
Münzerkenner
m
a
q
d
Mechanismus
zur Ausgabe einer
Getränkedose
Blockdiagramm
Folie 11-8
Schaltwerke
Beispiel
Unvollständig spezifiziertes Schaltwerk
Momentanzustand Eingänge
Folgezustand Ausgang
q1 q0
m1
m0
d 1 d0
a
0
0
0
1
1
0
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
0
1
X
0
1
1
X
1
1
1
X
1
1
1
X
0
0
0
X
0
0
0
X
0
0
0
X
1
1
1
X
1
1
0
1
0
X
1
0
1
X
0
1
1
X
1
1
1
X
Der Münzerkenner kann / darf
niemals das Signal 11 erzeugen
(siehe Kodierung). Also kann
die Eingabe 11 nicht auftreten.
Die Maschine kann für 11 einen
beliebigen (´X´) Nachfolgezustand annehmen.
⇒ die Übergangs- und
Ausgabefunktion haben eine
Don't Care-Menge,
"unvollständig spezifizierter"
Automat
kodierte Zustandstafel (unvollständig spezifiziert)
Folie 11-9
Schaltwerke
Unvollständig spezifiziertes Schaltwerk
Die Tatsache, dass uns für bestimmte Zustände das Verhalten des Automaten „egal“
ist, führt dazu, dass Übergangs- und Ausgabefunktion unvollständig spezifiziert
werden. Für bestimmte Zustände und bestimmte Eingaben existieren keine
Anforderungen hinsichtlich des Nachfolgezustands.
Während des Entwurfs können die durch die unvollständige Spezifikation
gegebenen Freiheitsgrade zur Optimierung ausgenutzt werden. Für die reale
Implementierung wird die Möglichkeit ausgesucht, die unter Kostengesichtspunkten
am günstigsten ist.
Wir legen im vorliegenden Fall (willkürlich) fest, dass der Automat bei Eingabe 11
in den Nachfolgezustand 00 übergeht.
Vergleiche dazu den Begriff des nicht-deterministischen Automaten: dort gilt, dass
ein Zustand für eine Eingabe in einen Zustand aus einer Menge von Zuständen
übergeht.
Folie 11-10
Schaltwerke
Beispiel
Momentanzustand Eingänge
Folgezustand Ausgang
q1 q0
m1
m0
d1
d0
a
0
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
0
1
0
0
1
1
0
1
1
1
0
1
1
1
0
0
1
0
0
1
0
1
0
0
1
1
0
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
0
0
1
1
0
1
1
Die Übergangsfunktion
und Ausgabefunktion
sind durch eine kombinatorische Schaltung
implementierbar. Die
kodierte Zustandstafel
ist die Wahrheitstabelle
für δ und λ.
kodierte Zustandstafel (vollständig spezifiziert)
Folie 11-11
Schaltwerke
Beispiel
Implementierung der Steuerung des Getränkeautomaten durch sequenzielle
Schaltung
m0
m1
a
d0
d1
q0
q1
D
längste Signallaufzeit durch
den kombinatorischen
Schaltungsteil bestimmt die
Taktperiode!
D
Takt
Folie 11-12
Schaltwerke
Moore- und Mealy-Version bei Schaltwerken
Moore-Schaltwerk
x1
x2
xn
z1
z2
kombinatorische
Schaltung
z1+
z2+
implementiert δ
zk
D
z k+
komb.
Schaltung
y1
y2
impl. λ
ym
Takt
Moore-Schaltwerk: Zustandssignale synchronisiert
Ausgangssignale synchronisiert
Folie 11-13
Schaltwerke
Moore- und Mealy-Version bei Schaltwerken
Mealy-Schaltwerk
x1
x2
xn
z1
z2
y1
y2
kombinatorische
Schaltung
ym
z1+
z2+
implementiert δ und λ
zk
D
z k+
Takt
Mealy-Schaltwerk: Zustandssignale synchronisiert
Ausgangssignale nicht synchronisiert ("asynchron")
Folie 11-14
Schaltwerke
Moore- und Mealy-Version bei Schaltwerken
Synchronisation der Ausgänge verwandelt Mealy-Maschine M in Moore-Maschine M´
z´ = (z, y)
x1
x2
xn
z1
z2
zk
D
λ´(z´) = y
y1
y2
kombinatorische
Schaltung
ym
implementiert δ´
z1+
z2+
δ´ = (δz´, δy´)
= (δ(x, z), λ(x, z)).
D
z k+
Takt
Äquivalente Moore-Maschine zur Mealy-Maschine der vorigen Folie
Folie 11-15
Schaltwerke
Binärspeicher
Im folgenden betrachten wir Möglichkeiten zur Realisierung von Binärspeichern, die
dazu dienen, den Momentanzustand eines Schaltwerks zu speichern. Diese Speicher
müssen zwischen vom Zustand 0 auf 1 umschalten (engl. flip) und von 1 auf 0
zurückfallen (engl. flop) können.
Es werden drei Typen von Flipflops (dt.: bistabile Kippschaltungen) unterschieden:
• ungetaktete Flipflops
• taktpegelgesteuerte Flipflops (Latches)
speichern neuen Wert, während das Taktsignal einen bestimmten Wert hat
• takflankengesteuerte Flipflops (oft nur als „Flipflops“ oder als „Register“ bezeichnet)
speichern einen neuen Wert, während das Taktsignal seinen Wert ändert
Folie 11-16
Schaltwerke
Binärspeicher
Einfache Schaltung mit Rückkopplung
Speicherelement erzeugt durch Zusammenschaltung von Gattern:
einfachster Gatterbaustein: Inverter
andere Möglichkeit: über Kreuz geschaltete NOR- und NAND-Gatter
"1"
"0"
kaskadierte Inverter:
statische Speicherzelle (allerdings ohne
Schreibzugriff…)
Folie 11-17
Schaltwerke
R-S-Flipflop (ungetaktet)
wie kaskadierte Inverter,
allerdings mit der Fähigkeit
den Ausgang auf 0 (reset)
oder 1 (set) zu stellen
r
s
über Kreuz
geschaltete NORGatter
r
q
r = 1, s = 0: q = 0 und q' = 1
r = 0, s = 1: q = 1 und q' = 0
r = 0, s = 0: speichern (hold)
r = 1, s = 1: ??
s
\q
Timing-Diagramm
Reset
Hold
Set
Reset
Set
100
r
s
q
\q
verbotener
Zustand
verbotener
Zustand
Folie 11-18
Wettlauf
Schaltwerke
R-S-Latch
taktpegelgesteuert ("level-sensitive")
\s
Schaltungsdiagramm:
\q
Schreibweise:
\r bedeutet: r ist "active low",
d.h. Rücksetzen bei "0"
\r
q
\en
Timing-Diagramm:
Reset
Set
100
\s
\r
\en
q
\q
Folie 11-19
Schaltwerke
D-Latch (Data, Delay)
taktpegelgesteuert ("level-sensitive")
Schaltungsdiagramm:
\q
d
\en
Funktionstabelle:
\en
d
0
0
1
0
1
X
q
q
Schaltsymbol:
\q
0 1
1 0
hold
D
Q
EN
Q
optional
Folie 11-20
Schaltwerke
Taktung und zeitliches Verhalten von Flipflops
Terminologie
Tsu
Th
Eingangssignal
Takt
Um
Umdas
dasTaktereignis
Taktereignisherum
herum
gibt
es
ein
"Zeitfenster",
gibt es ein "Zeitfenster",innerinnerhalb
dessen
sich
das
Eingangshalb dessen sich das Eingangssignal
signalnicht
nichtverändern
veränderndarf,
darf,um
um
korrekt
verarbeitet
zu
werden
korrekt verarbeitet zu werden
Takt:
Periodisches Ereignis, verursacht Zustandsänderung
des Speicherelementes
"steigende Flanke", "fallende Flanke",
"Pegel high", "Pegel low"
Setup-Zeit (Tsu)
minimale Zeitdauer, die das Eingangssignal stabil
sein muss, bevor das Taktereignis eintrifft
Hold-Zeit (Th)
minimale Zeitdauer, die das Eingangssignal stabil
bleiben muss, nachdem das Taktereignis eingetroffen
ist
Folie 11-21
Schaltwerke
Taktflankengesteuertes D-Flipflop
implementiert als Master-Slave-Flipflop
vorderflankengesteuert (positive/rising edge triggered)
Slave
Master
Q
D
Q
Q
D
D
CLK
EN
EN
D
Q
Clk
EN
hinterflankengesteuert (negative/falling edge triggered)
Slave
Master
Q
D
Q
Q
D
D
CLK
Schaltsymbol
Schaltsymbol
D
EN
Q
Clk
Folie 11-22
Schaltwerke
Zeitliches Verhalten bei Taktflankensteuerung
Typische Timing-Spezifikationen
74LS74: Flipflop
mit positiver
Flankensteuerung
•
•
•
•
Setup-Zeit
Hold-Zeit
Minimale Taktbreite
Verzögerungszeiten
(low nach high, high
nach low, maximal
und durchschnittlich)
D
Clk
Q
Tsu
20
ns
Th
5
ns
Tw
25
ns
Tplh
25 ns
13 ns
T su
20
ns
Th
5
ns
T phl
40 ns
25 ns
Alle Messungen beziehen sich auf das Taktereignis,
d.h. die steigende Flanke des Taktes
Folie 11-23
Schaltwerke
Vergleich von pegel- und flankengesteuerten D-Flipflops
zwei Arten von Binärspeichern:
7474
D
Q
Clk
flankengesteuertes
Flipflop (positive Flanke)
Flipflops (FFs): übernehmen Eingangswert bei Eintreffen
der Ereignisflanke als gespeicherten Wert.
Latches: übernehmen Eingangswert als gespeicherten Wert,
solange das Taktsignal einen bestimmten Pegel
besitzt. (Latch ist "transparent".)
Timing-Diagramm
7476
D
D
Q
EN
Clk
pegelgesteuertes
Latch
Clk
Q
7474
Q 7476
Verhalten ist gleich, außer wenn Eingang
sich ändert, während Takt high ist
Folie 11-24
Schaltwerke
Vergleich von vorder- und hinterflankengest. D-Flipflops
auch: „positive“ bzw. „negative“ Flankensteuerung
100
d
Clk
qpos
\qpos
qneg
\qneg
FF mit positiver
Flankensteuerung
FF mit negativer
Flankensteuerung
Positive Flankensteuerung
Negative Flankensteuerung
liest Eingänge bei steigender Flanke
Ausgänge wechseln nach steigender Flanke
liest Eingänge bei abfallender Flanke
Ausgänge wechseln nach fallender Flanke
Folie 11-25
Schaltwerke
Darstellung der Funktionalität eines RS-Flipflops
s
r
Übergangsfunktion
q
RS-Latch
KV - Diagramm für q+:
q+
s
sr
00
01
11
10
0
0
0
X
1
1
1
0
X
1
q
Die Übergangsfunktion ist von
Vorhandensein und Art der
Taktsteuerung unabhängig.
r
Zustandstafel
s
r
q
charakteristische Gleichung:
q+
q+ = s + r'q
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
0
1
1
X
X
HOLD
RESET
SET
VERBOTEN
Bei Speicherelementen wird
die Übergangsfunktion auch
als "charakteristische
Gleichung" bezeichnet.
Folie 11-26
Schaltwerke
JK-Flipflop (hier: ohne Takt; auch getaktet verfügbar)
Wie beseitigt man den verbotenen Zustand?
kopple Ausgangssignal zurück,
um sicherzustellen, dass r und s
niemals gleichzeitig 1 sind
Idee:
R
k
\Q
RSLatch
j
S
Q
j = k = 1: Toggle
Zustandstafel
charakteristische Gleichung:
j
k
q
q+
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
0
1
1
1
0
q+ = q k' + q' j
HOLD
RESET
SET
Toggle
\q
Schaltsymbol
J
Q
K
Q
Folie 11-27
q
Schaltwerke
Übersicht über die Flipflop-Typen
RS-Latch (Reset-Set):
Als Speicherelement nicht empfehlenswert wegen verbotenem Zustand!
jedoch fundamentaler Baustein für andere Flipfloptypen
JK-Flipflop (Jump-Kill):
breit einsetzbares Bauelement, getrennte Steuersignale für Setzen und Rücksetzen
oft nützlich
D-Flipflop (Data, Delay):
minimiert Verdrahtungsaufwand, in VLSI-Technologien bevorzugt,
einfachste Entwurfstechnik, am besten für Speicherregister geeignet
T-Flipflop (Toggle):
existieren nicht als eigenständige Bauelemente, werden aus einem der anderen
Flipfloptypen zusammengesetzt.
Eingang T=1: Ausgang wechselt. Eingang T=0: Ausgang bleibt konstant.
Gut für Zähler geeignet
Die verschiedenen Flipflop-Typen lassen sich mit Hilfe von kombinatorischer
Logik ineinander umformen. Die Art der Taktauswertung (pegelgesteuert oder
flankengesteuert) wird davon nicht beeinträchtigt.
Folie 11-28
Schaltwerke
Gegenseitige Implementierung von FF-Typen
"charakteristische Gleichungen":
RS:
q+ = s + r'q
D:
q+ = d
JK:
q+ = jq' + k'q
T:
q+ = tq' + t'q
Bestimme Ansteuerfunktion zur Implementierung von FF-Typ X mittels FF-Typ Y
durch Gleichsetzen der charakteristischen
Gleichungen von X und Y sowie
ggf. Fallunterscheidung zwischen
q = 0 und q = 1.
Implementierungen
d
J Q
Clk
K Q
q
k
D
j
D-FF implementiert mit JK-FF
(beide flankengesteuert)
Q
Clk Q
JK-FF implementiert mit D-FF
(beide flankengesteuert)
Folie 11-29
Schaltwerke
Schaltungwerksrealisierungen mit verschiedenen FF-Typen
Ansteuerungstabelle (hier für die 4 bekannten FF-Typen)
q
0
0
1
1
q+
0
1
0
1
r
X
0
1
0
s
0
1
0
X
j
0
1
X
X
k
X
X
1
0
t
0
1
1
0
d
0
1
0
1
"Ansteuerungstabelle":
Welche Eingaben sind notwendig, um
bestimmte Zustandsänderungen zu erzielen?
Vorgehensweise zur Implementierung eines Schaltwerks mit einem
vorgegebenen Flipflop-Typ
Falls D-Flipflop: Ansteuerfunktion ergibt sich aus den Folgezustandsspalten der
kodierten Zustandstafel.
Ansonsten:
• erweitere die Zustandstafel um Spalten für die Ansteuerung jedes Zustandsflipflops
• lies für jede Zeile und jedes Zustandsbit qi den Folgezustand qi+ ab
• entnimm der Ansteuertabelle die zum Paar (qi, qi+) gehörenden Werte der FF-Eingänge
(für den vorgegebenen FF-Typ)
• trage diese Werte in die zugehörigen neuen Spalten ein
Aus den neuen Spalten kann die Ansteuerfunktionen der Flipflops als Bündel
von Schaltfunktionen abgelesen und unter Nutzung der Don‘t Care‘s minimiert werden.
Folie 11-30
Schaltwerke
Beispiel: Getränkeautomat mit JK-FF
q
0
0
1
1
Momentanzustand Eingänge
j
0
1
X
X
q+
0
1
0
1
k
X
X
1
0
neue Spalten:
Folgezustand Ausgang
Flipflop-Ansteuerung
q1 q0
m1
m0
d1
d0
a
j1
k1
0
0
0
1
1
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
0
1
0
0
1
1
0
1
1
1
0
1
1
1
0
0
1
0
0
1
0
1
0
0
1
1
0
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
0
0
1
0
0
1
1
0
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
0
0
0
1
0
0
0
1
j0
k0
0
1
0
0
X
X
X
X
0
1
1
0
X
X
X
X
X
X
X
X
0
1
0
1
X
X
X
X
0
0
0
1
Folie 11-31
Technische Informatik I
Kapitel 12
Funktionseinheiten sequenzieller Systeme
Folie 12-1
Funktionseinheiten sequenzieller Systeme
Kapitelübersicht
Latches und Flipflops
bereits in Kap. 11 betrachtet
Register
• Speicherregister
• Schieberegister
Zähler
Random Access Memory (RAM)
• statisches RAM
• dynamisches RAM
Folie 12-2
Funktionseinheiten sequenzieller Systeme
Register
Speicherregister (lineare Speicher)
+
Fasse mehrere Flipflops gemäß der gegebenen
Darstellungsbreite zusammen
/Clr
D3
D
S
Q3
Q
R Q
D2
D
S
D
S
Q
Q1
Q
R Q
D0
D
S
TTL-Baustein
Q2
R Q
D1
Beispiel:
4-Bit Register aus 4 D-FFs
gemeinsames Takt- und Clear-Signal
Q0
asynchroner Reset:
Q wird 0 für Clr = 1,
unabhängig vom
Taktsignal
171
12
13
11
5
4
14
CLK
CLR
D3
D2
D1
D0
Q3
Q3
Q2
Q2
Q1
Q1
Q0
Q0
9
10
7
6
2
3
1
15
Q
Clk
R Q
"TTL 74171 Quadruple D-type FF with Clear"
(mit Angabe der Pinbelegung)
Folie 12-3
Funktionseinheiten sequenzieller Systeme
Register
Varianten von
Speicherregistern
Enable für Eingangssignale (Load)
Enable für Tri-State-Ausgänge
377
11
1
18
17
14
13
8
7
4
3
CLK
EN
D7
D6
D5
D4
D3
D2
D1
D0
Q7
Q6
Q5
Q4
Q3
Q2
Q1
Q0
19
16
15
12
9
6
5
2
"74377 Octal D-type FFs
with Enable"
11
18
17
14
13
8
7
4
3
374
CLK
H
QH
G
QG
F
QF
E
QE
D
QD
C
QC
B
QB
A
QA
OE
1
19
16
15
12
9
6
5
2
"74374 Octal D-type FFs
with Tri-state Outputs"
D-FFs mit postiver Flankensteuerung,
active low input enable (EN),
D-FFs mit positiver Flankensteuerung,
active low output enable (OE)
bei EN auf low und Taktübergang von
low nach high werden die Daten in
das Register geladen
wenn OE auf low ist, kann Registerinhalt
ausgelesen werden, sonst hohe Impedanz
Folie 12-4
Funktionseinheiten sequenzieller Systeme
Schieberegister
Oft sind Datentransfers zwischen benachbarten Zellen nötig
⇒ Speicher + Fähigkeit, Daten zwischen den Speicherelementen zu zirkulieren
+
Q2
Q3
Q4
Q1
\Reset
Schieberichtung
Schiebe
J SQ
CLK
K RQ
Q1
J SQ
CLK
K RQ
Q2
J SQ
CLK
K RQ
Q3
J SQ
CLK
K RQ
Q4
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
Schiebe
Schiebe
Shift
\Reset
+
hier: Realisierung mit Master Slave FF
Schiebe Flipflopinhalt bei jedem
Übergang des shift-Signals von
low auf high zum rechten Nachbarn
(gehe vom äußerst rechten Element
zum äußerst linken Element)
Master Slave FFs: lese Eingänge während
Takt high ist; ändere Ausgänge bei
Dieses Schieberegister ist nicht initialisierbar!
fallender Flanke
(externe Ein- und Ausgänge?)
Folie 12-5
Funktionseinheiten sequenzieller Systeme
Ein-/Ausgänge eines Schieberegisters
unterschiedliche Varianten und Ansteuerungsmöglichkeiten:
serielle oder parallele Eingänge
serielle oder parallele Ausgänge
Schieberichtung: links oder rechts
S1
S0
194
LSI
D
C
B
A
QD
QC
QB
QA
RSI
CLK
CLR
74194 4-bit bidirektionales
universelles Schieberegister
Implementierung:
serielle Ein-/Ausgänge:
parallele Ein-/Ausgänge:
Beispiel für einen universellen Schieberegisterbaustein:
- serielle Eingänge: LSI, RSI
- parallele Eingänge: A, B, C, D
- parallele Ausgänge: QA, QB, QC, QD
- clear-Signal
- positive Flankensteuerung
S1,S0 bestimmen den Schiebemodus
S1 = 1, S0 = 1: paralleles Laden von A, B, C, D in QA, QB, QC, QD
bei steigender Taktflanke (synchonous load)
S1 = 1, S0 = 0: schiebe bei steigender Taktflanke nach links
LSI ersetzt D
S1 = 0, S0 = 1: schiebe bei steigender Taktflanke nach rechts
RSI ersetzt A
S1 = 0, S0 = 0: speichere Zustand (hold)
keine Rückkopplung der ersten und letzten Stufe,
sondern externe Anschlüsse
Multiplexlogik am Eingang jedes internen FFs
Folie 12-6
Funktionseinheiten sequenzieller Systeme
Register
Beispiel: Parallel/Serien-Wandlung
Sender
D7
D6
D5
D4
Clock
parallele
Eingänge
(8 bit)
D3
D2
D1
D0
Empfänger
S1
S0 194
LSI
D
QD
C
QC
B
QB
A
QA
RSI
CLK
CLR
S1
S0 194
LSI
D
QD
C
QC
B
QB
A
QA
RSI
CLK
CLR
D7
D6
D5
D4
S1
S0 194
LSI
D
QD
C
QC
B
QB
A
QA
RSI
CLK
CLR
S1
S0 194
LSI
D
QD
C
QC
B
QB
A
QA
RSI
CLK
CLR
D3
D2
D1
D0
parallele
Ausgänge
(8 bit)
serielle
Übertragung
parallel einlesen:
Sender: S0 = S1 = 1
(1 Takt lang)
seriell übertragen:
Sender und Empfänger:
S0 = 1, S1 = 0
(8 Takte lang)
parallel auslesen:
Empfänger: S0 = 0, S1 = 0
(1 Takt lang)
z.B. Terminal → Telefonleitung → Rechner
Folie 12-7
Funktionseinheiten sequenzieller Systeme
Zähler
durchlaufe eine wohldefinierte Folge von Zuständen in Abhängigkeit
von einem Zählsignal
Merkmale von Zählern:
•
Steuersignal für Zählrichtung:
3 Bit Aufwärtszähler: 000, 001, 010, 011, 100, 101, 110, 111, 000, ...
3 Bit Abwärtszähler: 111, 110, 101, 100, 011, 010, 001, 000, 111, ...
•
Art des Zählcodes ist beliebig. (z.B.: binär, BCD, Gray-Code)
•
Steuersignale für Zählen/Laden/Anhalten
•
Synchrone/Asynchrone Nullstellmöglichkeit
Ein Schieberegister kann auch als Zähler aufgefasst werden.
Nachteil: pro Zählschritt ein Register (1000, 0100, 0010, 0001)
Folie 12-8
Funktionseinheiten sequenzieller Systeme
RAM-Speicherbausteine
Flipflops sind Schaltungen, mit denen sich 1 Bit Information speichern lässt.
Durch reguläre Anordnung von n Flipflops (Speicherzellen) und geeignete
Ansteuerung der Flipflopeingänge lassen sich Speicherbausteine für n Bit
Information realisieren. Die einzelnen Speicherzellen lassen sich beliebig
lesen und schreiben (engl. random access memory, RAM).
Flipflop-basierte Speicher halten die Information prinzipiell beliebig lange.
Man nennt sie SRAMs (engl. static RAMs).
Zur Speicherung von Information bietet sich auch die Ladung eines
Kondensators an. Über einen MOS-Transistor wird der Kondensator
aufgeladen oder entladen. Das Auslesen zerstört also die Information – sie
muss im Anschluss wieder neu eingeschrieben werden.
Ohne weitere Maßnahmen geht die Ladung des Kondensators durch
Leckströme verloren. Der Speicherinhalt muss daher regelmäßig aufgefrischt
(ausgelesen und neu eingeschrieben) werden. Man spricht deshalb von
DRAMs (engl., dynamic RAMs).
Folie 12-9
Funktionseinheiten sequenzieller Systeme
Static Random Access Memory (SRAM)
Reguläre Anordnung und Ansteuerung einzelner Flipflops erlaubt Realisierung mittelgroßer
Speicherbausteine. Beispiel: 256 Worte × 4 Bit, 4 Millionen Worte × 1 Bit.
Kein Refresh nötig, dafür aber relativ hoher Platzverbrauch (mehrere Transistoren pro Bit).
Dataj
Dataj
Data/Data: "Bitleitung"
Word Enable: "Wortleitung"
Word Enablei
Worte = Zeilen
Statische RAM-Zelle
Fasse mehrere Bits
zu Worten
zusammen.
Statische RAM-Zelle
1 Byte = 8 Bit
Statische RAM-Zelle
hier: jede Speicherzelle
besteht aus 6 Transistoren
Spalten = Bits
Betrachte im folgenden eine 1024 × 4 Architektur
Folie 12-10
Funktionseinheiten sequenzieller Systeme
Static Random Access Memory (SRAM)
Beispiel eines SRAM-Speicherbausteins
Chipauswahlleitung (active low):
bestimmt, ob Speicherinhalt geändert
werden kann
Write-Enable (active low)
bestimmt, ob gelesen oder geschrieben wird
10 Adressleitungen
4 bidirektionale Datenleitungen
1024 x 4 SRAM
CS
WE
A9
A8
A7
IO3
A6
IO2
A5
IO1
A4
IO0
A3
A2
A1
A0
Folie 12-11
Funktionseinheiten sequenzieller Systeme
SRAM - Speicherorganisation
A9
Speichermatrix
A8
Wähle
Zeile aus
64 x 64
quadratisches
Feld
A7
A6
Zeilendekoder
64 x 16
A5
64 x 16
64 x 16
64 x 16
⇒ besser
implementierbar
A4
A3
Wähle innerhalb einer
Zeile aus
A2
A1
Spaltendekoder
Leseverstärker u.
MUXs/DEMUXs
Leseverstärker
A0
CS
Datenpuffer
WE
I/O0
I/O1
I/O2
I/O3
Folie 12-12
Funktionseinheiten sequenzieller Systeme
Dynamic Random Access Memory (DRAM)
Speicherelement: 1 Transistor + 1 Kondensator
Lesen: aktiviere Wortleitung, stelle fest, ob Bitleitung
sich ändert
Wortleitung
Schreiben: aktiviere Wortleitung, setze Bitleitung auf 0
oder 1
Beachte:
Bitleitung
DRAM erlaubt höhere
Speicherkapazität auf einem
Chip als SRAM,
Lese- und Schreiboperationen
sind dafür aber langsamer!
Lesen zerstört Speicherinhalt
Speicherinhalt geht mit der Zeit (Millisekunden)
verloren: Auffrischen der Speicherzellen notwendig
Interne Schaltungen lesen Wort und schreiben es
gleich zurück
Beispiel: Speicher in einem PC
Hauptspeicher: DRAM
Cache: SRAM
Folie 12-13
Technische Informatik I
Kapitel 13
Aufbau eines Rechners
Folie 13-1
Struktur eines Computers
Aufbau eines
Rechners
Von Neumann - Rechner
• Rechner (Computer): Prozessoreinheit + Speicher (+ Ein-/Ausgabeeinheiten)
• Prozessoreinheit: Steuerwerk + Datenpfad (Operationswerk)
• Steuerwerk: endlicher Zustandsautomat
Eingabe: Maschinenbefehle, Datenpfadbedingungen
Ausgabe: Steuersignale für Registertransfers
Befehlsinterpretation: Befehl holen (Instruction Fetch), dekodieren, ausführen
• Datenpfad: funktionale Einheiten + Register
Funktionale Einheiten: ALU, Multiplizierer, Addierer, etc.
Register: Schieberegister, Speicherregister
Rechnerentwurf ist Beispiel für den Entwurf eines komplexen digitalen Systems.
Folie 13-2
Aufbau eines
Rechners
Struktur eines Computers
Darstellung als Blockdiagramm (ohne Ein-/Ausgabeeinheit)
Addresse
Central
Processing
Unit
(CPU)
Prozessor
Lesen/Schreiben
Speicher
Befehle, Daten
Operationstyp
Steuerwerk
Steuerungsbedingungen
Organisation der einzelnen
Verarbeitungsschritte und
ihrer zeitlichen Abfolge
Datenpfad
(Operationswerk)
Verarbeitung der
Daten
Folie 13-3
Struktur eines Computers
Aufbau eines
Rechners
Beispiel für Durchführung eines Befehls
Befehl: Addiere Rx zu Ry und lege Ergebnis in Rz ab
Schritt 1: hole den Befehl ADD aus dem Speicher und lade ihn ins Befehlsregister
Schritt 2: dekodiere den Befehl
Befehl im Befehlsregister ist ADD
Quelloperanden sind Rx, Ry
Zieloperand ist Rz
Schritt 3: führe Befehl aus
schicke Rx, Ry zur ALU
bereite ALU vor, ADD-Funktion auszuführen
addiere Rx zu Ry
schicke ALU-Ergebnis zu Rz
Folie 13-4
Struktur eines Computers
Aufbau eines
Rechners
unterschiedliche Arten von Befehlen
• Datenmanipulation (Registertransfer)
Addieren, Subtrahieren, etc.
Übertragung von Register zu Register
• Daten speichern
Lade/Speichere Daten aus/im Speicher
• Steuern
bedingte und unbedingte Verzweigungen
Aufrufen und Zurückkehren aus einer Unterroutine
Folie 13-5
Aufbau eines
Rechners
Struktur eines Computers
Steuerwerk
Elemente des Steuerwerks (Control Unit, Instruction Unit) sind die
üblichen Bestandteile von Schaltwerken:
•
•
•
•
Zustandsregister
Schaltlogik zur Berechnung der Nachfolgezustände
Schaltlogik zur Berechnung der Ausgangssignale
(Steuersignale für den Datenpfad)
plus zusätzliche Steuerregister:
•
Befehlsregister (Instruction Register (IR)):
speichert Befehl,
während er dekodiert wird
•
Programmzähler (Program Counter (PC)):
enthält Adresse des nächsten
auszuführenden Befehls
Folie 13-6
Aufbau eines
Rechners
Struktur eines Computers
Steuerwerk
0
Reset
Initialisiere
Maschine
Zustandsdiagramm
• Rücksetzen
holen
• Befehl holen
unterschiedlicher
Ablauf für jeden
Befehlstyp
• dekodieren
• ausführen
3 Arten von Befehlen:
Verzweigung
ausführen
• verzweigen
• laden/speichern
Zweig
genommen
lade/
ausspeichere führen
Registertransfer
ausführen
Zweig
nicht genominkremenmen
tiere PC
• Registertransfers
Folie 13-7
Aufbau eines
Rechners
Struktur eines Computers
Datenpfad
Cin
Arithmetische Schaltungen
entworfen auf
hierarchische und
iterative Weise
Ain
Bin
VA
Jedes Bit im Datenpfad
ist funktional gleich
4-bit
8-bit
16-bit
32-bit
64-bit
Datenpfade
Die arithmetischen Operationen
eines Prozessors werden in der
ALU (arithmetic logic unit)
zusammengefasst.
Sum
Cout
Ain
Bin
Sum
HA
Cout
HA
Cin
Hierarchischer Aufbau
eines Volladdierers
Folie 13-8
Aufbau eines
Rechners
Struktur eines Computers
Datenpfad
Blockdiagramm einer ALU
32
32
- Addition
- Subtraktion
- shift links
- shift rechts
- Komplement
-…
B
A
ALU
Operation
32
Cout S
32
Leitungsbündel
aus 32 Leitungen
Folie 13-9
Aufbau eines
Rechners
Struktur eines Computers
Blockdiagramm / Register-Transfer-Ebene
Speicherpfad
Ladepfad
Akkumulator (AC)
AC := AC <op> Mem
AC
Kontrollfluss
Datenfluss
n Bit breit
"single address
instructions"
AC impliziter Operand
A
FSM
B
ALU
MAR
Opcode
S
IR
FSM (finite state
machine):
Steuerwerk
SpeicherAdresse
Speicher
n Bit breit,
m Wörter
PC
Befehlspfad
Memory Address Register
hält die Adresse während des
Speicherzugriffs
Folie 13-10
Struktur eines Computers
Aufbau eines
Rechners
Blockdiagramm / Register-Transfer-Ebene
betrachte den Befehl: AC := AC + Mem<address>
1. Befehl holen (instruction fetch):
kopiere PC nach MAR
initiiere Lesesequenz für Speicher
schiebe Daten vom Speicher zum IR
2. Befehl dekodieren (instruction decode):
Op-code Bits von IR sind Eingangssignale des Steuerwerks
restliche IR Bits kodieren die Adresse des Operanden
Befehl: Einadressformat (n bit)
Operationscode
(Art des Befehls)
Angabe des (der) Operanden
Folie 13-11
Struktur eines Computers
Aufbau eines
Rechners
Blockdiagramm / Register-Transfer-Ebene
betrachte den Befehl: AC := AC + Mem<address>
3. Operand holen (Operand Fetch):
schiebe Operandenadresse von IR nach MAR
initiiere Lesesequenz für Speicher
4. Befehl ausführen (Instruction Execute):
Daten auf dem Ladepfad verfügbar
schiebe Daten zu ALU-Eingängen
konfiguriere ALU für ADD-Operation
schiebe Ergebnis von S nach AC
5. Programmverwaltung (Housekeeping):
inkrementiere PC, so dass PC auf nächsten Befehl zeigt
Folie 13-12
Aufbau eines
Rechners
Struktur eines Computers
Steuereinheit: übertrage Daten von einem Register zum anderen
setze geeignete Steuersignale
Notation für den Registertransfer
Befehl holen:
Befehl decodieren:
Befehl ausführen:
Setze Steuersignal
PC → MAR;
Memory Read;
Memory → IR;
Registertransfers
-- kopiere PC nach MAR
-- setze READ-Signal des Speichers
-- lade IR aus dem Speicher
IF IR<op code> = ADD_FROM_MEMORY
THEN
IR<addr> → MAR;
Memory Read;
-- kopiere Operandenadresse nach MAR
-- setze READ-Signal des Speichers
Memory → ALU B;
AC → ALU A;
ALU ADD;
-- leite Speicherinhalt an ALU B
-- leite AC an ALU A
-- befehle ALU, ADD auszuführen
ALU S → AC;
-- leite ALU-Ergebnis an AC
PC+1;
-- inkrementiere PC
Folie 13-13
Register-Transfer (RT) - Ebene
Aufbau eines
Rechners
Die hier verwendete Beschreibung des Aufbau eines Rechners ist im Vergleich
zur Beschreibung eines digitalen Systems auf Gatterebene abstrakter.
Digitale Systeme werden häufig auf der Register-Transfer-Ebene (RT-Ebene)
spezifiziert. Die RT-Beschreibung fasst das System als ein komplexes
Schaltwerk auf und gibt an, welche Übergänge in einem einzelnen Zeitschritt
stattfinden. Gegenüber der bisher verwendeten Beschreibung auf Gatterebene
("Bitebene") sind Abstraktionen möglich:
•
Mehrere Flipflops werden zu Register zusammengefasst und das Verhalten
des Systems durch Transfers von der Quell- zur Zielseite beschrieben.
⇒ "Register-Transfer-Ebene"
Beispiel: Abarbeitung eines Befehls im Prozessorkern
•
Bitvektoren zur Darstellung von Registerinhalten und Bitvektor-Operationen
zur Verknüpfung dieser Inhalte werden ebenfalls als primitive, vordefinierte
Datentypen angesehen ("Wortebene").
Folie 13-14
Aufbau eines
Rechners
Steuerwerk und Datenpfad
Aufteilung der CPU des Von Neumann-Rechners
Umgebung
Daten
Befehle
Operationswerk
(Datenpfad)
Steuerungsbedingungen
Ergebnis
Operationstyp
Steuerwerk
Die Aufteilung großer digitaler Systeme in Operationswerk (data path) und
Steuerwerk (control) ist ein wichtiges Grundprinzip zur Beherrschung der
Komplexität beim Entwurf.
Folie 13-15
Technische Informatik I
Kapitel 14
Entwurfsautomatisierung
Folie 14-1
Entwurfsautomatisierung
Entwurfsstile
Dieses Kapitel gibt einen ersten Einblick in den rechnergestützten Entwurf eines
mikroelektronischen Systems.
Layoutebene
Transistorebene
Gatterebene
1
x
y
Abstraktion
x
verschiedene
Siliziumschichten
implementieren
Transistoren
y
Abstraktion
x
y
x y
0 1
1 0
0
Implementierung logischer Funktionen durch MOS-Transistoren
Je nach geplanter Stückzahl und Anwendungsbereich der zu entwerfenden
Schaltung wählt man zwischen unterschiedlichen Entwurfsstilen aus.
Folie 14-2
Entwurfsautomatisierung
ASICs
Viele Entwurfsaufgaben können durch Standard-ICs (z.B. Standardbausteine wie in
Kap. 9, 11, 12, Mikrocontroller, Mikroprozessoren), die von zahlreichen Herstellern
angeboten werden, gelöst werden.
Oft ist es aber vorteilhaft, für die gegebene Anwendung einen speziellen Chip zu
entwickeln. Solche ASICs (application specific integrated circuits) werden mit
CAD-Werkzeugen entworfen, die eine Vielzahl von Entwurfsschritten
vollautomatisch durchführen.
Ein klassischer Entwurfsstil für ASICs ist der Standardzellenentwurf. Der gesamte
Entwurf wird in relativ kleine Einheiten (z.B. Gatter, Flipflops), so genannte
"Standardzellen", aufgeteilt, die getrennt entworfen werden können. Der
Abstraktionsgrad für die Zellaufteilung ist die logische Ebene (Gatterebene). Die
Zellen haben alle die gleiche Höhe, lediglich ihre Breite kann variieren. Die Zellen
werden meistens manuell entworfen und in einer Zellbibliothek zusammengefasst.
Für den Standardzellenentwurf stehen ausgereifte CAD-Werkzeuge zur Verfügung.
Folie 14-3
Entwurfsautomatisierung
Standardzellen-Layout
VDD
vertikales
Verdrahtungsraster
GND
horizontaler
Verdrahtungskanal
I/O Pads
horizontaler
Verdrahtungskanal
horizontaler
Verdrahtungskanal
Zellen
(AND, OR, NAND,
NOR, XOR, NOT,
AOI, Flipflop)
horizontaler
Verdrahtungskanal
GND
VDD
Struktur eines Standardzellenentwurfs
Folie 14-4
Entwurfsautomatisierung
CAD-basierter Entwurf
Hardwarebeschreibungssprachen (VHDL, Verilog) gestatten die Spezifikation
des Entwurfs auf höherer Ebene. Synthesewerkzeuge setzen die Spezifikation
automatisch in eine detaillierte Beschreibung des physikalischen Entwurfs um.
Beispiel: Addierer
1. Schritt:
Abstrakte Spezifikation durch spezielle Beschreibungssprachen
für Hardware (VHDL, Verilog)
entity VHDL is
port(
A, B : in INTEGER range 0 to 7;
C : out INTEGER range 0 to 7;
);
end VHDL;
architecture VHDL_1 of VHDL is
begin
C <= A + B;
end VHDL_1;
Folie 14-5
Entwurfsautomatisierung
Logiksynthese
2. Schritt: Logiksynthese
- Übersetzung der Spezifikation in unoptimierte Netzliste aus elementaren
logischen Grundfunktionen (UND, ODER, NICHT)
Je nachdem, welcher Abstraktionsgrad für die Spezifikation gewählt wurde, ist
dieser Schritt mehr oder weniger aufwändig. In der heutigen industriellen
Praxis ist der Abstraktionsgrad noch relativ nahe an der Struktur der
entstehenden Netzliste, so dass dieser Abbildungsschritt relativ einfach ist.
Andernfalls, wenn die Spezifikation das Verhalten des Systems auf hoher
Abstraktionsebene beschreibt, sind Techniken der "High-Level"-Synthese
erforderlich.
- "Technologieunabhängige" Optimierung der Netzliste
Information über den konkreten Implementierungsstil, wie beispielsweise die
Eigenschaften der Standardzellen einer gegebenen Bibliothek, wird noch nicht
benutzt. In der Regel wird nur die Anzahl der Literale in den zugrunde
liegenden Booleschen Gleichungen minimiert.
Folie 14-6
Entwurfsautomatisierung
Logiksynthese
(Forts.)
- Anpassung der optimierten technologieunabhängigen Darstellung an
Implementierungsstil (technology mapping)
Im Falle des Standardzellenentwurfs: Darstellung der Netzliste durch Elemente
der Zellbibliothek, Optimierungen (Fläche, Laufzeit) unter Ausnutzung der
physikalischen Eigenschaften der gegebenen Standardzellen
(technologieabhängige Optimierung)
1-bit Addierer auf Gatterebene
Folie 14-7
Entwurfsautomatisierung
Layoutgenerierung
3. Schritt: physikalischer Entwurf (Layoutgenerierung)
- Platzierung der Zellen auf dem Chip
- Verdrahtung der platzierten Zellen
- Dimensionierung der Transistoren zur Optimierung von Fläche und Signallaufzeit,
(große Gatter sind schnell, kleine Gatter sind langsam).
Polysiliziumbahn
VDD
Transistor
Diffusionsgebiete
VSS
Ai Bi
Carry_ini
Carry_outi Si
1-bit Addierer auf physikalischer Ebene
Folie 14-8
Entwurfsautomatisierung
Verifikation
Simulation
Aus einzelnen kombinatorischen und sequenziellen Schaltungskomponenten werden
hochkomplexe Systeme zusammengesetzt. Das Zusammenwirken zwischen den
Komponenten ist oft schwer zu durchschauen, so dass „Entwurfsfehler“ (design bugs)
niemals auszuschließen sind.
Daher ist die „Verifikation“ der spezifizierten Komponenten und des Gesamtsystems
sehr wichtig.
Verifikation durch Simulation:
Erstelle ein Modell des Systems. Lege Stimuli an die Eingänge des
System(modell)s an und untersuche das Verhalten des Modells für diese
Eingaben.
Simulation auf allen Entwurfsebenen zur Validierung der Korrektheit
des Entwurfs
Folie 14-9
Entwurfsautomatisierung
Verifikation
Formale Verifikation
Simulation macht nur Stichproben ⇒ unvollständig!
"Formale" Verifikation: mathematisch exakt, vollständiger Beweis der Korrektheit,
gewinnt industriell stark an Bedeutung
Verifikation durch formale Verifikation:
Erstelle ein Modell des Systems. Formuliere eine wünschenswerte Eigenschaft des
Systems in einer Sprache wie Prädikatenlogik. Untersuche, ob das System(modell)
die Eigenschaft (ausgedrückt als prädikatenlogische Formel) erfüllt.
Praxis: die Verifikation großer Systeme durch Prädikatenlogik ist meist nicht
handhabbar. (Man bedenke die grundsätzliche Nicht-Entscheidbarkeit!)
Deswegen beschränkt man sich in der Praxis auf "einfachere" Logiken wie bestimmte
temporale Logiken oder Aussagenlogik.
Diese Techniken sind Gegenstand der Vorlesung
„Hardware Verification and Quality Assessment“.
Folie 14-10
Entwurfsautomatisierung
Verifikation
Beispiel: Äquivalenzvergleich
Formaler Äquivalenzvergleich zur Verifikation der Optimierungsschritte: Bugs
in Synthesesoftware und manuelle Eingriffe des Designers können zu Fehlern in
der Implementierung führen.
Schaltung vor
Optimierung
a
b
1?
...
Schaltung nach
Optimierung
Schaltungen sind äquivalent und Implementierung korrekt, wenn Ausgangssignal nicht erfüllbar ist. Werkzeuge zum Äquivalenzvergleich beruhen auf
Verfahren zur Überprüfung der Erfüllbarkeit einer Booleschen Funktion
(„SAT-solving“).
Folie 14-11
Technische Informatik I
Prof. Dr. Martin Radetzki
Universität Stuttgart
Anhang N
Analyse umfangreicher elektrischer Netzwerke
Folie 4-1
Elektrischer Strom und elektrische Netzwerke
Netzwerkanalyse
Ziel der Netzwerkanalyse ist die Berechnung aller Ströme und Spannungen
an den einzelnen Bauelementen.
Bsp.: Wie groß sind die Spannungen an den Widerständen R1 bis R5 und wie
groß sind die Ströme durch die Widerstände? Wie groß ist der Strom, den die
Gleichspannungsquelle liefert?
Wir benötigen zur Beantwortung dieser Fragen das Ohm'sche Gesetz sowie
die Kirchhoffschen Gesetze (Maschenregel und Knotenregel).
Folie 4-2
Elektrischer Strom und elektrische Netzwerke
Kirchhoff'sche Gleichungen
Maschenregel
r r
∫ E ⋅ ds = 0
⇒ U R1 + U R 3 − U R 4 = 0
∑U = 0
Masche
Die Summe aller Spannungen beim Umlauf in einer
geschlossenen Masche ist Null.
Spannungen, deren Zählpfeil dabei entgegen der
Umlaufrichtung verläuft, werden negativ gezählt.
Folie 4-3
Elektrischer Strom und elektrische Netzwerke
Kirchhoff'sche Gleichungen: Knotenregel
Knotenregel
Ein Schaltungsknoten
hat keine Kapazität.
Alle Ladung, die in ihn
hineinfließt, muss auch
wieder aus ihm
herausfließen.
⇒
I R1 − I R 3 − I R 5 = 0
∑I = 0
Knoten
Die Summe aller in einen Knoten hineinfließenden
Ströme ist Null.
Ströme, deren Zählrichtung vom Knoten wegzeigt,
werden dabei negativ gezählt.
Folie 4-4
Elektrischer Strom und elektrische Netzwerke
Analyse umfangreicher Netzwerke
Beobachtung:
Mit Hilfe des Ohm'schen Gesetzes allein können in den Zweigen eines
Netzwerkes von den Größen (Ströme und Spannungen) alle bis auf eine
bestimmt werden.
Beispiele:
Folie 4-5
Elektrischer Strom und elektrische Netzwerke
Analyse umfangreicher Netzwerke
•
•
•
In jedem Zweig eines Netzwerks verbleibt eine Unbekannte.
Hat das Netzwerk z Zweige, so benötigt man z linear unabhängige *
Gleichungen zur Berechnung der z Unbekannten.
Zur Aufstellung der z Gleichungen stehen uns die Maschenregel und die
Knotenregel (Kirchhoff'sche Sätze) zur Verfügung.
Systematische Vorgehensweise beim Aufstellen der Gleichungen:
1. Schritt: Darstellen des Netzwerkgraphen
2. Schritt: Festlegen der Zählrichtungen für Strom und Spannung
3. Schritt: Aufstellen der Knotengleichungen
4. Schritt: Aufstellen der Maschengleichungen
* Eine Gleichung ist linear unabhängig von anderen Gleichungen, wenn sie
sich nicht durch lineare Überlagerung wie Addition oder Subtraktion aus
anderen Gleichungen herleiten lässt.
Folie 4-6
Elektrischer Strom und elektrische Netzwerke
1. Darstellen des Netzwerkgraphen
Das Netzwerk wird ohne die
Komponenten nochmals als
Netzwerkgraph dargestellt.
Die Knoten und Zweige des
Netzwerkgraphen stellen die
Struktur der Schaltung dar.
Folie 4-7
Elektrischer Strom und elektrische Netzwerke
2. Festlegen der Zählrichtungen
1.
2.
3.
Für jeden Zweig wird vereinbart, in welcher Richtung der Strom positiv
gezählt werden soll. (Diese Festlegung ist willkürlich und hat keinen
Einfluss auf das Ergebnis.)
An Verbraucher-Zweipolen wird die Zählrichtung für die Spannung in
Richtung des Stromes festgelegt.
An Erzeuger-Zweipolen wird die Zählrichtung entgegen der
Stromrichtung festgelegt.
U1
U0
U5
U4
U3
U2
Folie 4-8
Elektrischer Strom und elektrische Netzwerke
3. Aufstellen der Knotengleichungen
Besitzt ein Netzwerk k Knoten, so können k–1 linear unabhängige
Knotengleichungen aufgestellt werden. Von den k Knoten bleibt also einer
unberücksichtigt. (Die Auswahl des unberücksichtigten Knotens hat keinen
Einfluss auf das Ergebnis).
Beispiel:
–I4
=0
K1: +I0 –I1
K2:
+I1
–I3
–I5 = 0
K3:
–I2 +I3 +I4
=0
K4:
–I0
+I2
+I5 = 0
Die Gleichung für Knoten 4
ergibt sich als negative Summe
der anderen Gleichungen – ist also
linear abhängig von den anderen –
und wird nicht weiter betrachtet.
Folie 4-9
Elektrischer Strom und elektrische Netzwerke
4. Aufstellen der Maschengleichungen
Besitzt ein Netzwerk z Zweige und k Knoten, so müssen zusätzlich zu den k–1
Knotengleichungen noch m = z – (k–1) Maschengleichungen aufgestellt
werden. Diese Maschengleichungen müssen so ausgewählt werden, dass die
resultierenden Gleichungen linear unabhängig sind.
Es gibt verschiedene systematische Ansätze, sicherzustellen, dass die
Maschengleichungen linear unabhängig sind. Man sorgt dafür, dass in jeder
Masche ein Zweig enthalten ist, der in keiner anderen Masche vorkommt.
Wir betrachten im Folgenden zwei Methoden:
1. Methode des vollständigen Baumes
2. Methode der Auftrennung der Maschen
Folie 4-10
Elektrischer Strom und elektrische Netzwerke
4.1 – Maschengleichungen anhand des vollständigen Baumes
Zunächst verbindet man alle k Netzwerkknoten entlang der Zweige so
miteinander, dass keine geschlossene Masche entsteht. Die erzeugte Struktur
ist ein vollständiger Baum des Graphen und enthält k–1 Zweige.
Vollständiger Baum
(Beispiel 1)
Vollständiger Baum
(Beispiel 2)
Die im vollständigen Baum fehlenden z – (k–1) = m Zweige des
ursprünglichen Netzwerkes heißen Verbindungszweige.
Folie 4-11
Elektrischer Strom und elektrische Netzwerke
(4.1 – Maschengleichungen anhand des vollständigen Baumes)
Für das Aufstellen der Maschengleichungen wählt man die Maschen so, dass
jeder Verbindungszweig in genau einer Masche enthalten ist.
Maschen für die drei Verbindungszweige (Beispiel 2 der vorherigen Folie)
Maschengleichungen:
M1: –U0 +U1
+U5 = 0
M2:
+U2 +U3
–U5 = 0
M3: –U0
–U3 +U4 +U5 = 0
Folie 4-12
Elektrischer Strom und elektrische Netzwerke
(4.1 – Maschengleichungen anhand des vollständigen Baumes)
Nach Anwendung des Ohm'schen Gesetzes stehen nun z Bestimmungsgleichungen für die z unbekannten Größen des Netzwerkes zur Verfügung.
Im Beispiel:
Knotengleichungen:
Maschengleichungen
nach Anwendung des
Ohm'schen Gesetzes:
K1:
K2:
K3:
M1:
M2:
M3:
+I0
–I1
+I1
–I4
–I2
+R1 I1
–I3
+I3
–I5
+I4
=0
=0
=0
+R5 I5 = U0
+R2 I2 +R3 I3
–R5 I5 = 0
–R3 I3 +R4 I4 +R5 I5 = U0
Mit Hilfe dieser Gleichungen können die z = 6 Zweigströme I0 ... I5
berechnet werden und daraus dann die Zweigspannungen.
Folie 4-13
Elektrischer Strom und elektrische Netzwerke
4.2 Maschengleichungen durch Auftrennen der Maschen
Die Methode "Auftrennen der Maschen" ist eine weitere Möglichkeit, auf
systematische Weise linear unabhängige Maschengleichungen zu erhalten.
Man wählt zunächst einen beliebigen Maschenumlauf und stellt die
zugehörige Gleichung auf. Diese Masche wird jetzt an einem beliebigen
Zweig aufgetrennt, der in folgenden Maschen nicht mehr verwendet werden
darf. Mit dem verbleibenden Netzwerk verfährt man genauso, d.h., man wählt
den nächsten Maschenumlauf, stellt die Gleichung auf, und trennt die Masche
wieder auf.
Die fortgesetzte Anwendung dieser Methode liefert ebenfalls die benötigten
m = z – (k–1) Gleichungen.
Folie 4-14