alte Klausur - Bernd Baumgarten

Logik-Klausur, Beispiel, Seite 1
Alte Logik-Klausur
Name: ............................................................ Vorname: .......................................................
Matrikelnummer: .......................................................
1 (6)
2 (8)
3 (8)
4 (8)
5 (10) 6 (9)
7 (12) 8 (10) 9 (11)
Σ (82)
Note
14
WICHTIG
•
Die Klausur ist umfangreich. Dafür sind die geforderten
Punktzahlen für die Noten aber entsprechend niedriger.
•
Es gibt keine Minuspunkte; also bei Unsicherheit am Ende
bitte mindestens auf Verdacht markieren bzw. eintragen!
•
Hinten ist Platz für Notizen bzw. Neuberechnungen.
Bitte ggf. ungültig Gewordenes streichen.
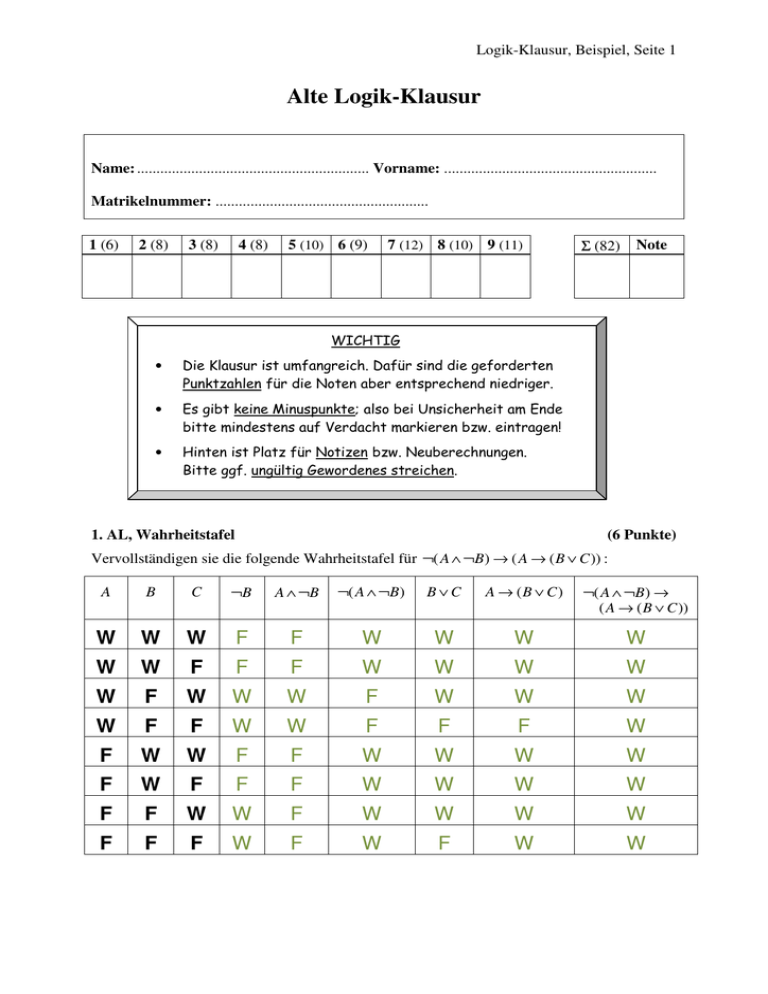
1. AL, Wahrheitstafel
(6 Punkte)
Vervollständigen sie die folgende Wahrheitstafel für ¬( A ∧ ¬B ) → ( A → ( B ∨ C )) :
A
B
C
¬B
A ∧ ¬B
¬( A ∧ ¬B )
B∨C
A → (B ∨ C)
¬( A ∧ ¬B ) →
( A → ( B ∨ C ))
W
W
W
F
F
W
W
W
W
W
W
F
F
F
W
W
W
W
W
F
W
W
W
F
W
W
W
W
F
F
W
W
F
F
F
W
F
W
W
F
F
W
W
W
W
F
W
F
F
F
W
W
W
W
F
F
W
W
F
W
W
W
W
F
F
F
W
F
W
F
W
W
Logik-Klausur, Beispiel, Seite 2
2. AL, Semantische Begriffe
(8 Punkte)
Wenn ϕ die Eigenschaft in Spalte 1 hat und ψ hat die Eigenschaft in Spalte 2, hat dann die
Formel in Spalte 3 die angegebene Eigenschaft?
Bitte antworten Sie jeweils in Spalte 4 entweder
• IMM, wenn dies immer der Fall ist,
• NIE, wenn dies nie der Fall ist,
• ABH sonst (wenn das also von ϕ und ψ abhängt, d.h. die Formel in Spalte 3 die
Eigenschaft in manchen Fällen hat, in manchen Fällen nicht.)
Tipps:
Denken Sie an einfache Beispiele für ϕ und ψ : A, B, ¬A, ¬B, A∧¬A, A∨¬A.
Widerlegbares kann unerfüllbar sein, Erfüllbares kann allgemeingültig sein.
1
Wenn ϕ … ist
2
und ψ ist … ,
3
ist dann …
4
Antwort
a)
allgemeingültig
unerfüllbar
ϕ ∧ψ
erfüllbar?
b)
allgemeingültig
erfüllbar
ϕ ∧ψ
kontingent?
c)
allgemeingültig
widerlegbar
ϕ ∧ψ
widerlegbar?
d)
kontingent
erfüllbar
ϕ →ψ
erfüllbar?
e)
allgemeingültig
kontingent
ϕ ∨ψ
kontingent?
f)
kontingent
erfüllbar
¬ϕ → ψ
g)
widerlegbar
erfüllbar
ϕ ↔ψ
h)
unerfüllbar
allgemeingültig
¬ϕ → ψ
erfüllbar?
kontingent?
allgemeingültig?
Erläuterungen:
a)
b)
c)
d)
e)
f)
g)
h)
T∧⊥ ≡ T, ist allgg., also erfb.
T∧T ≡ T, ist allgg., also nicht kont., T∧ A ≡ A, ist kont.
Wo ψ F ist, ist ϕ ∧ ψ auch F.
Wo ϕ F ist, ist ϕ → ψ W.
T∨ψ ≡ T, also nicht kont.
Wo ϕ T ist, ist ϕ → ψ W.
A ↔ A ist allgg., also nicht kont., A ↔ B ist kont.
… → ψ ist immer W, wo ψ W ist.
NIE
ABH
IMM
IMM
NIE
IMM
ABH
IMM
Logik-Klausur, Beispiel, Seite 3
3. AL, KNF-Umformung, Allgemeingültigkeit von KNF
(5+3 Punkte)
a) Formen Sie ¬( A ∧ ¬B ) → ( A → ( B ∨ C )) per syntaktischer Umformung gemäß
Vorlesung Schritt für Schritt in eine äquivalente KNF-Formel um.
Tipp: Das Distributivgesetz funktioniert auch so: (ϕ ∧ ψ ) ∨ ρ = (ϕ ∨ ρ ) ∧ (ψ ∨ ρ ) .
¬( A ∧ ¬B ) → ( A → ( B ∨ C ))
¬¬( A ∧ ¬B) ∨ ( A → ( B ∨ C ))
( A ∧ ¬B) ∨ ( A → ( B ∨ C ))
( A ∧ ¬B) ∨ (¬A ∨ ( B ∨ C ))
( A ∨ (¬A ∨ ( B ∨ C )) ∧ (¬B ∨ (¬A ∨ ( B ∨ C )))
( A ∨ ¬A ∨ B ∨ C ) ∧ ( ¬ B ∨ ¬A ∨ B ∨ C )
b) Erklären Sie überzeugend*, warum die Formel ( A ∨ ¬A ∨ B ∨ C ) ∧ (¬B ∨ ¬A ∨ B ∨ C )
allgemeingültig ist.
*) Also mehr als nur „weil sie immer wahr ist“, sondern warum das der Fall ist.
Tipp: Dafür hatten wir einen besonderen Satz kennengelernt.
Die KNF-Formel ist allgemeingültig, weil in jeder ihrer Klauseln zwei
gegensätzliche Literale stehen.
(Immer muss eines von diesen, und dadurch die ganze Klausel*, wahr sein.
*) Faustregel: Mit ODER kann’s nur wahrer werden (mit UND nur falscher).
Logik-Klausur, Beispiel, Seite 4
4. AL, Resolution
(4+4 Punkte)
Beweisen Sie die Allgemeingültigkeit von (¬A ∧ C ) ∨ ( A ∧ ¬B ) ∨ ¬C ∨ (C ∧ B) , indem Sie
die Negation dieser Formel nach den Gesetzen von de Morgan
(1. Negation der ∨-Kette,
2. Negation der ∧-Ketten,
3. Mehrfachnegationen beseitigen)
in eine äquivalente KNF umformen und auf die so erhaltene Formel (in KNF-Mengenform)
Resolution anwenden.
a) KNF-Umformung
¬((¬A ∧ C ) ∨ ( A ∧ ¬B) ∨ ¬C ∨ (C ∧ B) )
≡ ¬(¬A ∧ C ) ∧ ¬( A ∧ ¬B) ∧ ¬¬C ∧ ¬(C ∧ B)
≡ (¬¬A ∨ ¬C ) ∧ (¬A ∨ ¬¬B) ∧ C ∧ (¬C ∨ ¬B)
≡ {{ A, ¬C}, {¬A, B}, {C}, {¬C , ¬B}}KNF
pro Schritt 1 Punkt
b) Resolution
pro neuem Knoten (abgeleitete Klausel) 1 Punkt, zusammen höchstens 4 – und die auch
nur, wenn erfolgreich. Es gibt viele korrekte Lösungen, darunter auch welche mit Erfolg
bereits nach 3 neuen Knoten (auch 4 P.).
A, ¬C
¬A, B
¬C , ¬B}
C
A
B
¬C
∅
Logik-Klausur, Beispiel, Seite 5
5. AL, Tableauverfahren
(10 Punkte)
Beweisen Sie die Allgemeingültigkeit von ¬( A ∧ ¬B ) → ( A → ( B ∨ C )) , indem Sie mit der
Tableaubaum-Methode zeigen, dass die Negation ¬[¬( A ∧ ¬B ) → ( A → ( B ∨ C ))]
unerfüllbar ist.
• Schreiben Sie immer links vom Knoten eine laufende Nummer und rechts davon, von
welchem Knoten er mit einer Tableauregel herkommt.
• Kennzeichnen Sie abgeschlossene (widersprüchliche) Zweige durch X.
(1) ¬[¬( A ∧ ¬B ) → ( A → ( B ∨ C ))]
( 2)
¬( A ∧ ¬B )
(1)
¬( A → ( B ∨ C ))
A
¬( B ∨ C )
¬B
¬C
(3)
(4)
(5)
(6)
(7)
(8)
¬A
X
(2)
(9) ¬¬B
(10) B
X
(1)
(3)
(3)
(5)
(5)
(2)
(9)
Alternative (Beispiel):
(3)
¬( A → ( B ∨ C ))
(4)
¬A
(6)
A
(8) ¬( B ∨ C )
X
(2)
(3)
(3)
(5)
¬¬B
(7)
B
(9)
A
(10) ¬( B ∨ C )
(11)
¬B
(12)
¬C
X
1 pro Formel und 1 pro X, max. 10
Es gibt noch weitere korrekte Lösungen.
(1)
(2)
(5)
(3)
(3)
(10)
(10)
Logik-Klausur, Beispiel, Seite 6
6. ML, modale Formeln, PLTL, ω-reguläre Ausdrücke, Büchi-Automaten
(9 Punkte)
Wir betrachten jetzt ausschließlich Folgen von Situationen, in denen genau eines von a, b
oder c gilt, d.h. G ((a ∧ ¬b ∧ ¬c) ∨ (¬a ∧ b ∧ ¬c) ∨ (a ∧ ¬b ∧ c)) und für alle anderen
Aussagevariablen P gilt: G ¬P .
Nun seien wie folgt elf ω-Sprachen (Folgenmengen) über dem Alphabet {a, b, c} definiert –
sei es
• natürlichsprachlich,
• als ω-regulärer Ausdruck,
• mittels einer PLTL-Formel oder
• durch einen Büchi-Automat:
L1 :
L2 :
Unmittelbar auf c folgt nie b.
L3 :
(aa | b | c)ω
L4 :
(b | c * a)ω | (b | c * a) * cω
a’s kommen jeweils nur genau zu zweit hintereinander vor, d.h. wenn vor
einem a kein a steht, dann folgt unmittelbar noch ein a und unmittelbar darauf
kein a.
ω
L6 :
¬F( c ∧X b )
L7 :
G c →¬X b
L5 :
(aab | aac | b | c)
L8 :
[(a ∧ Xa ∧ XX¬a ) ∨ ¬a ] ∧ G( (¬a ∧ Xa ) → XX (a ∧ X¬a ) )]
c
L9 :
a
c
a,b
a,b,c
a
L10 :
a
L11 :
a
a,b,c
b,c
b,c
Tragen Sie die Sprachen („ Ln “) in die folgenden Kästen so ein, dass gleiche Sprachen im
gleichen Kasten stehen und unterschiedliche Sprachen in verschiedenen Kästen. Es kann sein,
dass nicht alle Kästen benutzt werden müssen.
L1 L4 L6
L9
kein cb
L2 L5 L8
aa* nur als
aa
L3 L10
L7 L11
a* nur als
a2n
alles, d.h.
(a|b|c)*
Achtung L7: Es heißt ja nicht G( c →¬X b ) – das wäre L1 !
Kommentare
Logik-Klausur, Beispiel, Seite 7
7. ML, Multimodallogik
(9+3 Punkte)
H
2
2
A
I, G2
1
1
C
B
2
2
2
D
E, U
1
F, G1
Das Diagramm zeigt Teile eines Spiels, bei dem 1 und 2 abwechselnd ziehen, d.h. generell
gilt iT→¬ i iT (i = 1 oder 2). Die Situationen sind durch Aussagensymbole A, B, C, D,
E, F, Gi, H, I und U dargestellt. In der derzeitigen Anfangssituation gilt A, und 1 ist am Zug.
• U bedeutet: Das Spiel endet unentschieden.
• G1 (bzw. G2) bedeutet: 1 (bzw. 2) hat gewonnen.
a)
i.
Schreiben Sie multimodale Formeln (mit i, i, i = 1 oder 2) für …
Es gibt keinen jetzt möglichen Zug von Spieler 1, nach dem dann sofort D gilt:
¬
ii.
1 ist dran und kann sicher erreichen, dass er/sie in genau drei Zügen gewinnt:
1
iii.
1D
2
1G1 *)
D gilt am Anfang nicht:
¬D
iv.
1 ist dran, und D könnte möglicherweise nach dem übernächsten Zug gelten:
1
v.
Nach dem nächsten Zug (von 1) kann 2 mit seinem Zug ein Unentschieden erreichen:
1
vi.
2U
1 kann nicht in genau drei Zügen verlieren:
¬
b)
2D
1
2
1G2,
1
2
1(G1∨U)
Bitte kreisen Sie die Nummern derjenigen der obigen Aussagen ein, die in der
abgebildeten Interpretation wahr sind:
i
ii
iii
iv
v
vi
*) weil im Diagramm alle 1-Nachfolger 2-Nachfolger haben. Ganz allgemein könnte man dies
mit … ∧ 1 2T explizit fordern.
Logik-Klausur, Beispiel, Seite 8
8. PL1, Werkzeugkasten
(10 Punkte)
Zeigen Sie mithilfe des AL&PL1-Werkzeugkastens, dass folgende Folgerung gilt:
∀x(∃yR( x, y ) → P ( x)) |= P (a ) ∨ ¬R (a, b)
indem Sie unten die fehlenden Begründungen eintragen (Ann. oder Regelkürzel, Nummer(n)
der Prämissen).
(1)
∀x(∃yR ( x, y ) → P ( x))
.................. geg.
Zeige P (a ) ∨ ¬R (a, b)
(2)
¬( P (a ) ∨ ¬R (a, b))
..................... Ann.
(3) |
¬P (a ) ................................ 2, NOB
(4) |
¬¬R (a, b) ............................ 2, NOB
(5) |
R ( a , b)
(6) |
∃yR (a, y ) ............................. 5, EE
(7) |
∃yR (a, y ) → P (a )
(8) |
P (a ) .................................. 6,7 MP
............................... 4, DNB
.................... 1, Sp
(9) | ⊥ ..................................... 3,8 WE
(10)
P ( a ) ∨ ¬R ( a , b )
......................... IB
1 P. pro Begründung, außer
2 P. für je 6 und 7
Logik-Klausur, Beispiel, Seite 9
9. PL1, Resolution
(11 Punkte)
Zeigen Sie per Resolution mit Unifikation, dass die Formel
∀x∀x∀x[ P ( f ( g (a ), x)) ∧ ¬Q (c) ∧ (¬P ( f ( y, b) ∨ R ( y, z )) ∧ (¬R ( g (a ), c) ∨ Q ( z ))]
unerfüllbar ist.
• Tragen Sie die abgeleiteten Klauseln (in PL1: Mengen (evtl. verneinter) atomarer
Formeln) in die -Kästen ein.
• Tragen Sie die verwendeten allgemeinsten Unifikatoren (Substitutionen im Stile von
[u,w/h(a,v)),b ] ) in die -Kästen ein,
P ( f ( g ( a ), x ))
¬Q(c )
¬P ( f ( y, b)) , R ( y , z )
¬R ( g (a ), c ) , Q ( z )
[ z / c]
[ y , x / g (a ), b ]
¬R ( g ( a ), c )
R ( g ( a ), z )
[ z / c]
∅
2 P. pro Unifikation (gestrichelt berandet). 1 P. wenn darin eine Richtug vertauscht ist
1,5 pro Resolutionsschritt (bei „leicht falschen“ 0,75, bei richtiger Resolvente aus
falscher Unifikation 1P.)
10,5 wird aufgewertet
11