Affindrehung - AMG Bensberg

ABITURWISSEN IM LEISTUNGSKURS MATHEMATIK
1
Definition der Proportionalität: Zwei Größen x und y heißen genau dann proportional zueinander, wenn das Verhältnis y:x
konstant ist, d.h. wenn es eine Konstante k gibt, für die gilt: y : x  k . k heißt Proportionalitätsfaktor.
Für proportionale Größen gilt z.B.: Verdoppelt sich die eine Größe, so verdoppelt sich auch die andere Größe.
Definition der Antiproportionalität: Zwei Größen heißen genau dann antiproportional (oder „umgekehrt proportional“), wenn
ihr Produkt konstant ist, d.h. wenn es eine Konstante c gibt, für die gilt: x  y  c .
Für antiproportionale Größen gilt z.B.: Verdoppelt sich die eine Größe, so halbiert sich die andere Größe.
1.
Der Betrag: Unter dem Betrag ( auch Absolutbetrag genannt) einer Zahl versteht man den Abstand, den diese Zahl auf der
Zahlengeraden von der Zahl 0 besitzt. Der Betrag jeder Zahl ist  0 . Formal wird der Betrag folgendermaßen definiert:
 a für a  0
Für den Betrag einer Summe gilt der folgende Satz (Dreiecksungleichung): | a  b || a |  | b |
| a | 
 a für a  0
2.
Das Pascaldreieck ist ein Zahlendreieck, Formel zur Berechnung der Zahlen des Pascaldreiecks:
Das Pascalsche Dreieck das in der obersten Zeile (=Zeile Nr.0)
Die Zahl aus Zeile Nr.n und Spalte Nr.k
nur eine 1 stehen hat und dann von Zeile (Die Spalten verlaufen parallel zu der linken Dreieckssei1
zu Zeile eine Zahl mehr erhält. Vorne
te. Die ganz linke Spalte mit lauter Einsen hat die Nr. 0)
11
und hinten in jeder Zeile steht eine 1.
n!
121
berechnet sich nach folgender Formel:
.
Die restlichen Zahlen entstehen durch
k!(n  k )!
13 31
Addition
der
beiden
schräg
darüber
14 6 41
stehenden Zahlen.
Man nennt diese Zahl  n  .
.......... .
k
3.
Binomische Formeln: 1.) (a  b)2  a 2  2ab  b2
2.) (a  b) 2  a 2  2ab  b 2
3.) (a  b)  (a  b)  a 2  b2
Höhere Potenzen der Binome: (a  b)3  a 3  3a 2b  3ab2  b3 ; (a  b) 4  a 4  4a 3b  6a 2b2  4ab3  b4
Die Koeffizienten der Potenz (a  b) n sind die Zahlen  n ,  n ,  n ,...,  n  aus der Zeile Nr.n des Pascalschen Dreiecks.
 0 1  2 n
4.
Das Lösen von quadratischen Gleichungen: Zuerst wird die Gleichung in Normalform gebracht: x 2  px  q  0
2
p
p
Dann wird die p-q-Formel angewandt: x1 / 2       q . Der Radikand entscheidet über die Anzahl der Lösungen. Er
2
2
wird deshalb auch Diskriminante genannt. Falls die Diskriminante = 0 ist, gibt es eine Lösung, falls sie > 0 ist, gibt es zwei
Lösungen, falls sie < 0 ist, gibt es keine Lösungen.
Für den Fall, dass die Lösungen ganze Zahlen sind, lässt sich die Gleichung mit folgendem Satz lösen:
Vi ëtascher Wurzelsatz: x1  x 2  p und x1  x 2  q
5.
Potenzen: Ein Ausdruck der Form a x heißt Potenz. a heißt Grundzahl oder Basis, x heißt Hochzahl oder Exponent.
Es wird definiert: a 0  1 und a n  a  a  ...  a (n mal), wobei der Exponent n eine natürliche Zahl ist.
Für negative ganze Zahlen –n wird definiert: a  n 
1
n
p
. Für rationale Exponenten
p
q
q
wird definiert: a q  a p
a
x
y
xy
x
y
6.
Potenzgesetze: 1.) a  a  a
und a : a  a x  y
2.) a x  b x  (a  b) x und a x : b x  (a : b) x 3.) (a x ) y  a x  y
7.
Gegenkathe te
Gegenkathete
Ankathete
tan  
cos  
Sinus, Kosinus, Tangens: Im rechtwinkligen Dreieck gilt: sin  
Ankathete
Hypotenuse
Hypotenuse
8.
y
x
y
cos  
sin  
Trigonometrische Funktionen: Für beliebige Winkel wird im Einheitskreis (r=1) definiert: sin  
r
r
x
Dabei ist P(x|y) der Punkt, in dem der Strahl, der mit der x-Achse den Winkel  bildet, den Einheitskreis schneidet.
9.
sin 
Beziehungen zwischen den trigonometrischen Funktionen: sin 2  cos2  1 , tan  
cos 
10.
Additionstheoreme: sin(  )  sin  cos   cos  sin  , cos(  )  cos  cos   sin  sin 
11.
Logarithmen: Der Logarithmus einer Zahl z zur Basis a ist diejenige Hochzahl x, für die gilt: a x  z . Man schreibt:
x  log a z . Die Bestimmung des Logarithmus von einer Zahl nennt man Logarithmieren. Logarithmieren ist die Umkehrung des
Exponierens, so wie das Wurzelziehen (=Radizieren) die Umkehrung des Potenzierens ist.
Beispiel 1: Ich potenziere die Basis 2 mit der Hochzahl 3 und erhalte das Ergebnis 8.. Dieser Vorgang wird rückgängig gemacht
durch das Ziehen der dritten Wurzel. Ich erhalte die Basis 2 zurück.
Beispiel 2: Ich exponiere die 3 zur Basis 2 (d.h. ich „stelle die 3 heraus“ als Hochzahl oben an die 2) und erhalte als Ergebnis 8.
Dieser Vorgang wird rückgängig gemacht durch Logarithmieren zur Basis 2. Ich erhalte die Hochzahl 3 zurück.
12.
Logarithmusgesetze: 1.) log a (x  y)  log a x  log a y 2.) log a  xy   log a x  log a y 3.) log a ( x r )  r  log a x
 
Sat
ABITURWISSEN IM LEISTUNGSKURS MATHEMATIK
2
lg 1024
log a z
Umrechnungsformel: log b z 
Anwendung: log 2 1024 
 10 (Kann mit dem TR berechnet werden.)
log a b
lg 2
13.
Funktionen: Eine Zuordnung x  y , die jeder Zahl x aus einer Menge D (genannt: Definitionsmenge) genau eine Zahl y aus
einer Menge W (genannt: Wertemenge) zuordnet, heißt Funktion.
Bemerkung über Funktionen: Funktionen sind eindeutige Zuordnungen, insofern nämlich, als jedem x genau ein y zugeordnet wird. Es gibt immer genau einen Funktionswert für jedes x aus der Definitionsmenge der Funktion.
Für manche Funktionen gilt auch das Umgekehrte, dass nämlich zu jedem Funktionswert y auch nur genau ein x-Wert existiert.
Solche Funktionen heißen ein-ein-deutig oder umkehrbar eindeutig. Für solche Funktionen ist auch die umgekehrte Zuordnung y  x eine Funktion. Die ursprüngliche Funktion heißt deshalb auch umkehrbar.
14.
Umkehrfunktionen: f sei eine umkehrbare Funktion. Dann heißt die umgekehrte Zuordnung, die jedem y-Wert wieder seinen
x-Wert zuordnet, „Umkehrfunktion von f“. Man verwendet für die Umkehrfunktion von f das Symbol f 1 (Vorsicht: Das darf
nicht verwechselt werden mit der Funktion 1f .
15.
Satz über Umkehrbarkeit: Wenn eine Funktion über einem Intervall streng monoton ist, dann ist sie über diesem Intervall
auch umkehrbar.
16.
Bestimmung der Umkehrfunktion: Man erhält die Funktionsgleichung der Umkehrfunktion, indem man in der Gleichung der
Ausgangsfunktion x und y vertauscht und dann nach y auflöst.
Man erhält den Graphen der Umkehrfunktion, indem man den Graphen der Ausgangsfunktion an der ersten Winkelhalbierenden
spiegelt.
Beispiele für Umkehrfunktionen:
- Die Potenzfunktion y  x 2 ist umkehrbar über dem Intervall [0; [ . Die Gleichung der Umkehrfunktion lautet: y  x .
- Die Exponentialfunktion y  2 x ist über ganz IR umkehrbar. Die Gleichung der Umkehrfunktion lautet: y  log 2 x .
17.
Zahlenfolgen: Eine Funktion f mit dem Definitionsbereich IN und dem Wertebereich IR heißt Zahlenfolge. Die Funktionswerte
f(1), f(2), f(3), ... werden mit a1, a 2 , a 3 ,... bezeichnet und heißen Folgenglieder. Die ganze Folge wird mit dem Symbol
 a n  bezeichnet.
18.
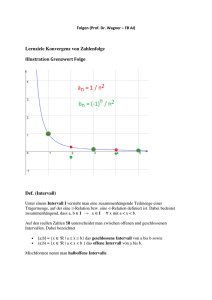
Grenzwert einer Zahlenfolge: Eine Zahl g heißt Grenzwert der Zahlenfolge  a n  genau dann, wenn gilt:
  0 N  IN n  N : | a n  g | 
Eine Zahlenfolge heißt konvergent gegen g genau dann, wenn sie den Grenzwert g besitzt.
Man schreibt:
lim a n  g
n 
19.
Unendliche Summern: Unendliche Summen (Bsp.: 1 
1
2

1
4
 ... ) sind spezielle Zahlenfolgen. Ihnen liegt eine andere Zahlen-
folge  a n  zugrunde, deren Teilsummen a1 , a1  a 2 , a1  a 2  a 3 , ... gebildet werden. Die Folge der Teilsummen einer
Folge heißt Reihe. Die unendliche Summe a1  a 2  a 3 +... ist ein Symbol für die Reihe und auch für den Grenzwert der Reihe,
falls ein Grenzwert existiert.
2
2
20.
n ( n 1)
n ( n 1)(2 n 1)
3
3
3
3 n ( n 1)
1

2

3

...

n

Potenzsummen: 1  2  3  ...  n 
; 12  22  32  ...  n 2 
;
6
2
4
21.
Grenzwert einer Funktion:
a) Grenzwert im Unendlichen: Eine Zahl g heißt Grenzwert der Funktion f für x   (bzw. x   ) genau dann, wenn gilt:
  0 N  IR x  N : | f (x)  g |  (bzw.   0 N  IR x  N : | f (x)  g |  )
Man schreibt: lim f (x)  g (bzw. lim f (x)  g )
x 
x  
b) Grenzwert an einer Stelle (lokaler Grenzwert): f sei eine Funktion und x 0 besitze eine Umgebung U, für die gilt:
U \ {x 0}  Df . Eine Zahl g heißt Grenzwert der Funktion an der Stelle x 0 genau dann, wenn jede gegen x 0 konvergierende
Zahlenfolge, deren Werte in U liegen, den Grenzwert g besitzt.
22.
Grenzwertsätze: f und g seinen zwei Funktionen.


Sowohl für den lokalen Grenzwert an einer Stelle x o  lim  als auch für den Grenzwert im Unendlichen  lim  gelten fol x  
 xx o 
gende Grenzwertsätze unter der Bedingung, dass die Grenzwerte lim f(x) und lim g(x) existieren:
1.) lim (f(x)+g(x))=lim f(x) + lim g(x)
2.) lim (f(x) - g(x))=lim f(x) - lim g(x)
3.) lim((f (x)  g(x))  lim f (x)  lim g(x)
4.) lim ((f(x):g(x)) = lim f(x) : lim g(x) falls lim g(x)  0.
23.
Stetigkeit: Eine Funktion f heißt stetig an der Stelle x o  Df genau dann, wenn der Grenzwert lim f(x) existiert und wenn
x  
gilt:
lim f(x) = f( x o ).
x  
24.
Differenzierbarkeit: Eine Funktion f heißt differenzierbar an der Stelle x o , wenn der Grenzwert
Sat
ABITURWISSEN IM LEISTUNGSKURS MATHEMATIK
3
f (x)  f (x o )
existiert. Man nennt diesen Grenzwert Ableitung von f an der Stelle x o und schreibt f ' ( x o ) .
lim
x  xo
x x o
Die Menge aller Stellen des Definitionsbereiches von f, an denen f differenzierbar ist, heißt Differenzierbarkeitsbereich von f.
Die Funktion, die jedem x aus dem Differenzierbarkeitsbereich von f den Wert f’(x) zuordnet, heißt Ableitungsfunktion von f.
25.
Ableitungsregeln: Es seien u und v zwei Funktionen. Überall, wo u und v differenzierbar sind, sind auch die Funktionen,
c  u (c konstant), u + v, u  v , u  v und u : v differenzierbar (letztere nur, wo v nicht Null ist) und es gilt:
Faktorregel: [c  u]'  c  u' Summenregel: [u  v)' u'v' Produktregel: [u  v]'  u'v  u  v'
'
u 'v  u  v'
u 
Quotientenregel:   
Für Potenzfunktionen gilt die Potenzregel: [ x n ]'  n  x n 1, n  IR
v
v2
26.
Das Integral: f sei eine Funktion und das Intervall [a;b] gehöre zum Definitionsbereich von f.
Über dem Intervall [a;b] wird zunächst eine „Linkssumme“ und eine „Rechtssumme“ definiert:
n 1
Für jede natürliche Zahl n wird definiert: L n :
Genau dann, wenn lim
n 
ba
ba
 f (i 
) und R n :
n
n
i 0

n
ba
ba
 f (i 
)
n
n
i 1

L n und lim R n existieren und übereinstimmen,
n 
b
nennt man diese Zahl das Integral von f über dem Intervall [a;b]. Man bezeichnet es mit dem Symbol:
 f (x )dx .
a
Falls über dem Intervall [a;b] gilt f (x)  0 , gibt das Integral genau die Flächenmaßzahl der Fläche an, die von der Kurve, der xAchse und den Geraden mit der Gleichung x=a und x=b begrenzt wird.
27.
Stammfunktion: Eine Funktion F heißt Stammfunktion einer Funktion f, wenn F differenzierbar ist und ihre Ableitungsfunktion f ist: F' (x)  f (x).
b
28.
Hauptsatz der Differential- und Integralrechnung: f ( x )dx = F(b)  F(a) , wobei F eine beliebige Stammfunktion von f ist.

a
29.
Flächeninhalt und Integral:
b
Falls f über dem Intervall [a;b] oberhalb der x-Achse verläuft, ist das Integral
 f (x )dx positiv und gibt genau den Flächeninhalt
a
zwischen Kurve und x-Achse über dem Intervall [a;b] an.
b
Falls f über dem Intervall [a;b] unterhalb der x-Achse verläuft, ist das Integral
 f (x )dx negativ und man muss den Betrag bila
den, um die Fläche zwischen Kurve und x-Achse über dem Intervall [a;b] zu erhalten.
Falls f teilweise oberhalb und teilweise unterhalb der x-Achse verläuft, heben sich die negativen und die positiven Flächenstücke gegenseitig auf, so dass das Integral über [a;b] nicht mehr die Fläche zwischen Kurve und x-Achse angibt.
30.
Berechnung von Flächeninhalten:
Aufgabentyp 1: Fläche zwischen Graph von f und x-Achse
Berechne die Nullstellen von f. Berechne dann lauter Einzelintegrale von Nullstelle zu Nullstelle. Bilde von diesen Einzelintegralen den Betrag und addiere die Beträge.
Aufgabentyp 2: Fläche, die von Graph f, x-Achse und den Geraden x=a und x=b eingeschlossen wird.
Berechne die Nullstellen von f, die im Intervall [a;b] liegen. Bilde dann die Teilintegrale von a bis zur 1. Nullstelle, von dieser
bis zur nächsten u.s.w.. Zuletzt das Integral von der letzten Nullstelle bis b. Rest wie oben.
Aufgabentyp 3: Fläche, die von Graph f und Graph g eingeschlossen wird.
Berechne die Schnittstellen x1, x 2 , x 3 ,... von f und g. Bilde dann die Differenzfunktion f(x) – g(x) und bilde Teilintegrale
x i 1
 f (x)  g(x) dx . Bilde von diesen den Betrag und addiere die Beträge.
xi
Aufgabentyp 4: Fläche, die begrenzt wird von Graph f, Graph g und den Geraden x=a und x=b.
Berechne die Schnittstellen von f und g, die im Intervall [a;b] liegen. Bilde dann die Differenzfunktion f(x) – g(x) und bilde
Teilintegrale von a bis zur ersten Schnittstelle u.s.w. Bilde von diesen den Betrag und addiere die Beträge.
b
Falls f und g keine Schnittpunkte in dem Intervall [a;b] besitzen, berechne direkt
 f (x)  g(x) dx .
a
31.
Rotationsvolumen: V    [f ( x )]2 dx
b

a
Sat
ABITURWISSEN IM LEISTUNGSKURS MATHEMATIK
4
32.
Integrationsregeln:

 c  f (x)  c  F(x)  C
Substitution 1: f (g(x)dx  f (u)du , wobei u=g(x).


Summenregel: f (x)  g(x)  F(x)  G(x)  C Faktorregel:
 u'v  u  v   u  v'
Substitution 2 : f (x)dx  f (g(t )  g' (t ) , wobei x=g(t).


Partielle Integration:
33.
Funktion
sin
Stammfunktion -cos+C
cos
sin+C
lnx
xlnx-x+C
ex
ex
ax
1
ln a
1
 ax  C
1  x2
arcsin x  C
1
1
1 x
arctan x  C
2
cos2 x
tan x  C
ANALYTISCHE GEOMETRIE
 



 
Geradengleichung in Parameterform : x  a  r  u
Ebenengleichung in Parameterform: x  a  r  u  s  v







Mittelpunkt der Strecke AB: m  12  (a  b)
Schwerpunkt des Dreiecks ABC: s  1  (a  b  c)
3


 a  rb
Teilpunktsatz: Wenn T die Strecke AB im Verhältnis r teilt (d.h. AT  r  TB ), dann gilt: t 
1 r


   
Skalarprodukt: a  b | a |  | b |  cos , wobei  der von a und b eingeschlossene Winkel ist.
 a1   b1 
a  b 
Koordinatendarstellung des Skalarproduktes:  1    1   a1b1  a 2b 2 und  a 2    b 2   a1b1  a 2b 2  a 3b3 .
a  b 
 a 2   b2 
 3  3
Bemerkung: Im folgenden wird das Symbol  für die skalare Multiplikation durch den einfachen Punkt ersetzt.


Geometrische Deutung des Skalarproduktes: Das Skalarprodukt zweier Vektoren a und b ist eine Zahl, deren Betrag dem



Flächeninhalt des Rechteckes entspricht, dessen Seiten so lang sind wie die Vektoren a b und b . Dabei ist a b die senkrechte


Projektion von a auf b .


Das Skalarprodukt ist positiv, falls der Winkel zwischen den Vektoren a und b spitz ist.


Das Skalarprodukt ist negativ, falls der Winkel zwischen den Vektoren a und b stumpf ist.
Orthogonalitätskriterium: Zwei Vektoren stehen genau dann orthogonal aufeinander, wenn ihr Skalarprodukt 0 ist.
Normalenformen der Ebenengleichung (bzw. der Geradengleichung im zweidimensionalen Raum):


  
a) Punktnormalenform: (x  p)  n  0 Dabei ist p ein Stützvektor und n ein Normalenvektor der Ebene (bzw. Gerade).
 
b) allgemeine Normalenform: x  n  d  0
 

Dabei ist d das Skalarprodukt x  n , das für jeden Ortsvektor x der Ebene die selbe Zahl ist.


Falls d positiv ist, zeigt n vom Ursprung aus zu der Ebene hin, falls d negativ ist, zeigt n von der Ebene weg,
falls d=0 ist, liegt der Ursprung in der Ebene.

 
c) Hessesche Normalenform: x  n o  d  0 Dabei ist n o ein Normalenvektor der Länge 1. Für d gilt:
d gibt des Abstand der Ebene (bzw. Gerade) vom Ursprung an.
Koordinatenform der Ebenengleichung: ax  by  cz  d bzw. ax  by  cz  d  0 Diese Form ist eine direkte Umformung der
a 
 
allgemeinen Normalenform: x  n  d  0   b   x  d  0  ax  by  cz  d  0
c
 
x y z
d) Achsenabschnittform der Ebenengleichung:    1 Diese Form entsteht aus der Koordinatenform, indem man
a b c
zuerst d auf die rechte Seite bringt, dann die ganze Gleichung durch d dividiert und auf der linken Seite so umformt, dass nur
noch x, y und z im Zähler stehen. Die Nenner a, b, c haben die Bedeutung, dass sie die Achsenabschnitte der Ebene auf den drei
Achsen angeben.
Abstand zweier paralleler Ebenen: Beide Ebenen müssen in der Hesseschen Normalenform mit demselben Normalenvektor
 
 
angegeben werden: E1 : x  n o  d1  0 und E 2 : x  n o  d 2  0 .
Dann gilt für den Abstand e der beiden Ebenen: e  d 2  d1 .
Abstand e eines Punktes R von einer Ebene E bzw. von einer Geraden g im zweidimensionalen Raum:
 
Wenn E bzw. g wie oben in der Hesseschen Normalenform gegeben ist, gilt für den Abstand: e | r  n  d |


 
a b  a 3b 2 
(1) a  b steht orthogonal zu a und zu b .
   2 3



Vektorprodukt: a  b   a 3b1  a1b3 
Es gilt: (2) a , b und a  b bilden ein Rechtssystem.
a b a b 
 
 
2 1
 1 2
(3) | a  b |= | a |  | b |  sin  .


 
(3) bedeutet geometrisch: | a  b | ist gleich dem Flächeninhalt des von a und b aufgespannten Parallelogramms.
Sat
ABITURWISSEN IM LEISTUNGSKURS MATHEMATIK
Flächeninhalt des Dreiecks ABC: F 
5
| AB |  | AC |  sin  oder mit dem Vektorprodukt: F  | AB  AC |
 

Spatprodukt: Unter dem Spatprodukt dreier Vektoren a, b und c versteht man den Term:
1
2
1
2
a1 b1 c1
  
  
(a  b)  c . Sein Wert entspricht dem Betrag einer Determinante: (a  b)  c  a 2 b 2 c 2 .
a 3 b 3 c3

  


Volumen des Spats: Der von den Vektoren a, b und c aufgespannte Spat hat das Volumen V  (a  b)  c
Volumen einer Pyramide mit den Eckpunkten A,B,C und D: V 
1
6
(AB  AC)  AD
 


v v
Schnittwinkel zweier Geraden: cos    1 2
Dabei sind v1 und v 2 die Richtungsvektoren der beiden Geraden.
| v1 |  | v 2 |
 


n n
Schnittwinkel zweier Ebenen: cos    1 2
Dabei sind n1 und n 2 die Normalenvektoren der beiden Ebenen.
| n1 |  | n 2 |
 


vn
Schnittwinkel von Gerade und Ebene: sin     Dabei ist v der Richtungsvektor der Geraden und n der Normalen| v || n |
vektor der Ebene.
Abstand eines Punktes P von einer Geraden g (im dreidimensionalen Raum):
Bestimme in Normalenform die Gleichung einer Ebene E, die P enthält und orthogonal zu g verläuft, d.h. verwende den Richtungsvektor von g als Normalenvektor von E. Berechne dann den Schnittpunkt S von g und E und berechne schließlich die Länge des Vektors PS .
Abstand paralleler Geraden: Man berechnet den Abstand eines Punktes der ersten Geraden von der zweiten Gerade.
 

 

Abstand zweier windschiefer Geraden: g1 : x  a  r  u und g 2 : x  b  s  v seien windschief. Man bestimmt mit den Rich

tungsvektoren u und v zwei Ebenen jeweils durch die Stützpunkte A bzw. B der beiden Geraden. Dann berechnet man den
Abstand dieser beiden Ebenen.
Kreis und Kugel: Der Kreis K im zweidimensionalen Raum bzw. die Kugel K im dreidimensionalen Raum hat die Gleichung:
 
K: [ x  m]2  r 2 Dabei ist M der Mittelpunkt und r der Radius des Kreises bzw. der Kugel.
Tangente bzw. Tangentialebene: Die Tangente an den Kreis K bzw. die Tangentialebene an die Kugel K im Berührpunkt B hat
 
 
die Gleichung: (b  m)  ( x  m)  r 2
Polare bzw. Polarebene: Die Polare zum Punkt P bzgl. des Kreises K bzw. die Polarebene zum Punkt P bzgl. der Kugel K hat
 
 
die Gleichung: (p  m)  ( x  m)  r 2
Definition der affinen Abbildung: Eine Abbildung der affinen Ebene (=zweidimensionaler affiner Raum) auf sich selbst heißt
genau dann affine Abbildung, wenn sie umkehrbar ist und eine Matrixdarstellung der folgenden Form besitzt:

 
 a
b1    c1 
x '  A  x  c bzw. x '   1
  x  c 
 a 2 b2 
 2
Matrixdarstellung spezieller affiner Abbildungen:

Zentrische Streckung mit Zentrum = und Spiegelung an der x-Achse:
Verschiebung um den Vektor v :
(Die Matrix ist die „Einheitsmatrix“) Streckfaktor k:





 
x '   k 0   x
x '   1 0   x
x '   1 0   x  v
0
k
0

1




0 1
Drehung um 90° um 0:
Spiegelung an der 1. WinkelhalbierenSpiegelung an der y-Achse:
den:
  0  1 




x'  
x '   0 1   x
x '    1 0   x
x
1
0
1
0
0
1






Spiegelung an einer Ursprungsgeraden, die Scherung mit der x-Achse als Achse und
Drehung um den Winkel  um 0:
mit der x-Achse den Winkel  einschließt: dem Scherungswinkel  :




cos   sin   
cos 2 sin 2  
x '   1 tan    x
x'  
x
x'  
x


0
1


 sin  cos  
 sin 2  cos 2 

 
Satz 1: Eine geometrische Abbildung der Form x '  A  x  c ist genau dann umkehrbar, wenn det(A)  0 .
Satz 2: Affine Abbildungen sind geradentreu und deshalb auch parallelentreu sowie teilverhältnistreu.
Satz 3: Die Bildpunkte dreier Punkte, die nicht auf einer Geraden liegen, legen eine affine Abbildung eindeutig fest.

 
Satz 4: (Bedeutung der Abbildungsmatrix) Ist eine affine Abbildung gegeben durch x '  A  x  c bzw.

 a
b1    c1 
a 
b 
x'   1
  x   c  , dann ist c  OO' und die Spalten  a 1  und  b 1  sind die Vektoren O ' E1 ' und O' E 2 '
a
b
2
 2
 2
 2
 2
Sat
ABITURWISSEN IM LEISTUNGSKURS MATHEMATIK
6
Dabei ist O der Ursprung, O’ sein Bild. E1 ist der Punkt (1|0) und E 2 ist der Punkt (0|1).
Erstellen der Matrixdarstellung aus drei gegebenen Bildpunkten: Gegeben sind A, B, C und ihre Bildpunkte A’, B’, C’.


 
Gesucht sind die Abbildungsmatrix A und der konstante Vektor c für die zugehörige affine Abbildung  : x '  A  x  c .
x ' a x  b x  c
1. Schritt: Schreibe die Abbildungsgleichung in Koordinatenform: x1 '  a1 x1  b1 x2  1c
2
2 1
2 2
2
2. Schritt: Setze in die erste Gleichung die Koordinaten der gegebenen Punkte und Bildpunkte ein. Es entsteht ein LGS
mit drei Gleichungen und drei Variablen. Löse es mit dem Gaußverfahren oder dem Determinantenverfahren.
3. Schritt: Verfahre genauso mit der zweiten Gleichung.
b1   c1 d1   a1c1  b1c 2 a1d1  b1d 2 
a
Definition der Matrizenmultiplikation:  1

 : 

a
b
2   c 2 d 2   a 2c1  b 2c 2 a 2d1  b 2d 2 
 2
Verkettung von affinen Abbildungen: Die Verkettung    zweier Abbildungen  und  ist definiert durch die Gleichung


x'  (( x) . Es gilt: Die Verkettung zweier affiner Abbildungen ist wieder eine affine Abbildung.
Die Abbildungsmatrix der Verkettung    ist die Matrix A  B . Achtung: Die Multiplikation von Matrizen ist nicht kommutativ. Genauso ist auch die Verkettung von Abbildungen nicht kommutativ.
 

 

 


Die Matrixdarstellung der Verkettung: Für  : x '  Ax  c und  : x'  Bx  d gilt:    : x '  ABx  Ad  c


Satz 5: Für die Matrizenmultiplikation und die Multiplikation mit einem Vektor gilt: A  (B  x)  (A  B)  x


Achtung! Aus A  x  B  x folgt nicht, dass A = B. (Gegenbeispiel:  3 2   1   5 0   1 )
  2 7  1  0 5  1
Umkehrabbildungen: Die Umkehrabbildung  1 einer Abbildung  ist definiert durch die Gleichungen  1    id und
   1  id . id ist die identische Abbildung (Identität), die jeden Punkt auf sich selbst abbildet. Die Umkehrabbildung bildet



jeden Bildpunkt auf sein Urbild zurück ab. D.h. ( 1 ( x))   1 ((x)) für alle Ortsvektoren x von Punkten der Ebene.
Satz 6: a ) Jede affine Abbildung besitzt eine Umkehrabbildung und diese ist wieder eine affine Abbildung.
b) Für die Matrix A 1 der Umkehrabbildung gilt: A  A 1  E und A 1  A  E (E ist die Einheitsmatrix.)
Inverse Matrix: Falls zu einer Matrix A eine Matrix A 1 existiert, für die gilt A  A 1  E und A 1  A  E , so ist diese eindeutig bestimmt. Man nennt sie die zu A inverse Matrix. A nennt man invertierbar.
1  b 2  b1 
b1 
a
1
Satz 6: Falls A =  1
nach folgender Formel: A 1 

.
 invertierbar ist, berechnet sich A
a
b
det(
A)   a 2 a1 
2
 2
Satz 7: Eine Matrix A besitzt genau dann eine inverse Matrix, wenn det(A)  0.




 
Matrixdarstellung der Umkehrabbildung:  : x '  Ax  c hat die Umkehrabbildung  1 : x '  A 1x  A 1c
Satz 8: Die affinen Abbildungen bilden bzgl. der Verkettung eine Gruppe und die 2  2 -Matrizen bilden bzgl. der Matrizenmultiplikation eine Gruppe.
Flächeninhalt eines Parallelogramms: Ist A eine 2  2 -Matrix, dann ist der Betrag der Determinante von A gleich dem Flächeninhalt des von den Spaltenvektoren aufgespannten Parallelogramms.
Bedeutung der Determinante der Abbildungsmatrix: A sei die zu einer affinen Abbildung gehörige Matrix. Dann ist det(A)
ein Maß für den Verzerrungsgrad der Abbildung. Genauer: |det(A)| ist der Faktor, mit dem sich der Flächeninhalt einer Figur
beim Abbilden vervielfacht. Ist det(A)>0 bleibt der Umlaufsinn der Figuren erhalten, ist det(A)<0 kehrt er sich um.
Die zu einer affinen Abbildung gehörende Vektorabbildung: Zu jeder affinen Abbildung (die ja Punkte der Ebene auf Punkte
der Ebene abbildet) gehört eine Vektorabbildung, die den Verbindungsvektoren AB beliebiger Punkte A und B den Verbin
 


dungsvektor A' B' der beiden Bildpunkte zuordnet. Zu  : x '  Ax  c gehört die Vektorabbildung  * : v'  Av


b1 
a
Definition: Ist  * : v'  Av mit A =  1
 eine Vektorabbildung, dann nennt man die quadratische Gleichung
 a 2 b2 
a1  
b1
 0 bzw. 2  (a1  b 2 )  (a1b 2  a 2 b1 )  0 charakteristische Gleichung von  * (bzw. von A). Die Löa2
b2  


 
sungen heißen Eigenwerte von  * (bzw. von A). Vektoren v  0 , für die gilt Av  v heißen Eigenvektor von  * .
Affine Abbildungen mit dem Fixpunkt 0
Euler-Affinität
Streckscherung
Affindrehung
(zwei Eigenwerte)
(ein Eigenwert)
(kein Eigenwert)
Sonderfälle:
Sonderfälle:
Sonderfälle:
Parallelstreckung (ein Eigenwert ist 1) Scherung (   1 , 1-dim. Eigenraum)
Drehung
Schrägspiegelung (Eigenwerte 1; -1)
Zentrische Streckung (2-dim Eigenr.) Drehstreckung

 
Fixpunkte affiner Abbildungen: Ein Punkt F heißt Fixpunkt der affinen Abbildung  : x '  Ax  c , wenn F auf sich selbst
  

abgebildet wird. Es gilt dann für seinen Ortsvektor f gilt:  : Af  c  f . Eine Gerade g heißt Fixgerade der Abb., wenn das
Bild von g wieder g ist. (Jeder Punkt von g wird dann wieder auf g abgebildet.) Eine Gerade g heißt Fixpunktgerade der Abb.,
wenn jeder Punkt von g Fixpunkt ist.
Es gilt: Wenn   id, besitzt  entweder genau einen Fixpunkt, eine Fixpunktgerade oder keinen Fixpunkt.
Sat
ABITURWISSEN IM LEISTUNGSKURS MATHEMATIK
7
Sat