P ( w 1 )

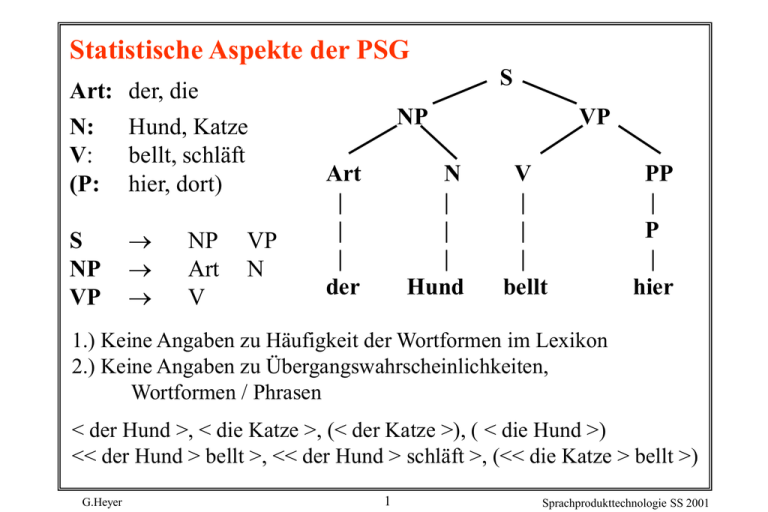
Statistische Aspekte der PSG
S
Art: der, die
N:
V:
(P:
Hund, Katze
bellt, schläft
hier, dort)
S
NP
VP



NP
Art
V
VP
N
NP
Art
|
|
|
der
N
|
|
|
Hund
VP
V
|
|
|
bellt
PP
|
P
|
hier
1.) Keine Angaben zu Häufigkeit der Wortformen im Lexikon
2.) Keine Angaben zu Übergangswahrscheinlichkeiten,
Wortformen / Phrasen
< der Hund >, < die Katze >, (< der Katze >), ( < die Hund >)
<< der Hund > bellt >, << der Hund > schläft >, (<< die Katze > bellt >)
G.Heyer
1
Sprachprodukttechnologie SS 2001
Alternatives Modell: endlicher Automat mit
Übergangswahrscheinlichkeiten
0,5 hier
0,5 der
0,5 Hund
0,5 die
0,5 Katze
0,5 bellt
O
0,5 schläft
0,5 dort
Problem: Weder die Übergangswahrscheinlichkeiten noch
das zugrunde liegende Netzwerk (Automat) sind bekannt.
Black Box
" der" "Hund" " ? "
Modell ?
G.Heyer
2
Sprachprodukttechnologie SS 2001
Aufgaben: 1. Berechnung der Übergangswahrscheinlichkeiten
2. Präzisierung der probabilistischen Automaten
Statistische Grundlagen
Notation
Sei X eine Zufallsvariable mit einer endlichen Menge V(X)
von m Ereignissen.
| X = x | sei die Anzahl von Ereignissen bei denen
X den Wert x hat ( d. h. x  V(X)).
Die Wahrscheinlichkeit des Auftretens von xi ( Abkürzung
P(xi) ist:
| xi |
P (X = xi ) =
m

j=1
G.Heyer
| xj |
3
Sprachprodukttechnologie SS 2001
Beispiel:
Sei W das Auftreten einer bestimmten Wortform wi aus der
Menge der m Wortformen eines Textes.
Die Wahrscheinlichkeit des Auftretens der i-ten Wortform wi
ist dann:
| wi |
P (W = wi ) =
m
 | wj |
j=1
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten eines Ereignisses X unter
der Voraussetzung , dass das Ereignis y schon eingetreten ist,
heißt bedingte Wahrscheinlichkeit P ( x | y ).
P(x|y)=
G.Heyer
P(x,y)
P(y)
4
Sprachprodukttechnologie SS 2001
Sind x und y voneinander unabhängig, so gilt:
P ( x, y ) = P ( x ) * P ( y )
Die bedingte Wahrscheinlichkeit unabhängiger Ereignisse ist:
P(x|y)=P(x)
Beispiel:
Die bedingte Wahrscheinlichkeit des Aufeinanderfolgens
zweier Wortformen ist:
P (W2 = wj | W1 = wi ) =
G.Heyer
| W1 = wi , W2 = wj |
| W1 = wi |
5
Sprachprodukttechnologie SS 2001
Bayessches Gesetz
Wenn die Ereignisse x  V (x) einander paarweise ausschließen
und die Menge der m Elementarereignisse ausschöpfen, so gilt
für die bedingte Wahrscheinlichkeit:
P(x)*P(y|x)
P(x|y)=
P(y)
Verallgemeinerungen
P ( w, x | y, z )=
P ( w, x) * P ( y, z | w, x )
P ( y, z )
P ( w1, w2, w3, ... , wn ) = P ( w1 ) * P ( w2 | w1 ) *
P (w3 | w1, w2 ) . . . *
P (wn | w1, . . . , w n-1)
G.Heyer
6
Sprachprodukttechnologie SS 2001
Anwendung: Statistisches Modell der Deutschen Sprache
Weise allen Folgen von Wortformen der Länge n eine
Wahrscheinlichkeit zu, d. h.
P ( W1,n = wi,n )
für alle Folgen w1,n .
W1,n ist eine Folge von n Zufallsvariablen w1, w2, ... , wn ,
die jeweils irgendeine Wortform des Deutschen als Wert
nehmen können, und w1,n ist eine konkrete Folge von
deutschen Wortformen.
Diese Folge kann auf der Grundlage der verallgemeinerten
Bayesschen Regel berechnet werden.
P ( w1,n ) = P ( w1 ) * P ( w2 | w1 ) * P ( w3 | w1,2 ) * . . .
* P ( wn | w1,n-1 )
G.Heyer
7
Sprachprodukttechnologie SS 2001
Als Berechnungsgrundlage dient ein n-gram Modell,
d. h. die Annahme, dass nur die vorangehenden n-1
Wortformen von Einfluss auf die Wahrscheinlichkeit der
nächsten Wortform sind, wobei n = 3 ( daher tri-gram )
P ( wn | w1, ... , wn-1) = P (wn | wn-2, wn-1 )
P ( w1,n )
= P (w1 ) * P (w2 | w1 ) * P ( w3 | w 1,2 ) *
... * P (wn | wn-2,wn-1 )
n
= P (w1 ) * P ( w2 | w1 ) *  P ( wi | wi-2,i-1 )
i=3
n
=
 P (wi | wi-2,wi-1)
i=1
G.Heyer
8
Sprachprodukttechnologie SS 2001
Beispiel:
Um ein Trigram-Modell zu erzeugen, wird in einem
Trainingstext gezählt, welche Paare und Tripel von Wörtern
wie oft auftreten.
" Der Hund bellt und die Katze schläft. "
< Der Hund >
< Der Hund bellt >
< Hund bellt >
< Hund bellt und >
< bellt und >
< bellt und die >
C (wi-2, i )
(Tripel)
Pe (wi | wi-2, i-1 ) =
C ( wi-2, i-1 )
G.Heyer
9
Sprachprodukttechnologie SS 2001
Anwendung
Das Problem der Spracherkennung lässt sich beschreiben als
das Finden derjenigen Wortfolge w1,n, durch die
P ( W1,n = w1,n | Lautfolge)
maximiert wird.
Unter Anwendung der Bayesschen Regel lässt sich das
Problem in zwei Teile zerlegen, in die
Wahrscheinlichkeitsverteilung einzelner Lautfolgen (z.B. im
Deutschen) und in die Wahrscheinlichkeitsverteilung
einzelner Wortformen (sog. Sprachmodell ) :
P (w1,n ) * P ( Lautfolge | w1,n )
P ( w1,n | Lautfolge ) =
P ( Lautfolge )
Da der Nenner für alle w1,n gleich bleibt, muss nur der Zähler
maximiert werden.
G.Heyer
10
Sprachprodukttechnologie SS 2001
Markov Modelle
Es sei X = ( X1, ... , XT ) eine Folge von Zufallsvariablen mit
Werten in einer endlichen Menge S = { S1, ... , SN } , dem
Zustandsraum.
X ist eine Markov-Kette oder ein Markov-Modell, wenn die
folgenden Markov-Eigenschaften erfüllt sind:
Abhängigkeit vom vorherigen Zustand
P ( Xt+1 = Sk | X1, ... , Xt ) = P ( Xt+1 = Sk | Xt )
Zeitinvarianz
P ( Xt+1 = Sk | X1 , ... , Xt ) = P ( X2 = Sk | X1 )
G.Heyer
11
Sprachprodukttechnologie SS 2001
Als Darstellung wird gewöhnlich ein (nichtdeterministischer )
endlicher Automat gewählt,
bei dem die Kanten mit Übergangswahrscheinlichkeiten
gekennzeichnet sind.
(Alle ausgehenden Kanten eines Knotens summieren sich
zu 1).
Wird bei einem Markov-Modell nicht nur der vorangehende
Zustand, sondern m Zustände zur Vorhersage des nächsten
Zustands verwendet, spricht man von einem
Markov-Modell m-ter Ordnung.
Jedes n-gram Modell ist äquivalent zu einem
Markov-Modell (n-1)-ter Ordnung.
G.Heyer
12
Sprachprodukttechnologie SS 2001
Versteckte Markov-Modelle (Hidden Markov Models )
Im Unterschied zu sichtbaren Markov-Modellen gelten für
versteckte Markov-Modelle folgende Bedingungen:
1.) Die Übergänge von einem Knoten zum nächsten sind
nicht sichtbar, lediglich die Wahrscheinlichkeit des
Endzustandes ist bekannt.
2.) Einem Zustand können mehrere Übergänge mit
demselben Symbol zugeordnet sein.
G.Heyer
13
Sprachprodukttechnologie SS 2001
Ein HMM ist ein Quadrupel
< s1, S, W, E >
mit S einer Menge von Zuständen.
s1  S dem Anfangszustand des Modells
W
der Menge der Ausgangszeichen und
E
der Menge der Übergänge (edges), wobei jede Menge
geordnet ist:
S = < s1, s2, . . . , s >
W = < w1, w2, . . . , w >
E = < e1 , e 2 , . . . , e >
G.Heyer
14
Sprachprodukttechnologie SS 2001
Ein Übergang ist eine Quadrupel
< si, sj, wk, p >
mit
si  S
sj  S
wk  W
und p
dem Ausgangszustand,
dem Endzustand
dem Ausgangszeichen ( das von dem
Modell akzeptiert oder generiert wird
der Wahrscheinlichkeit des Übergangs .
Wir schreiben einen Übergang:
si
wk
sj
(Ein Zustand a kann der Ausgangszustand für mehrere
Übergänge sein, die dasselbe Ausgangssymbol haben, aber in
verschiedene Endzustände übergehen.)
G.Heyer
15
Sprachprodukttechnologie SS 2001
Die Wahrscheinlichkeit p eines Übergangs
wk
si
sj
,
wk
p si
sj
ist definiert als die Wahrscheinlichkeit, dass zu einem
Zeitpunkt t das HMM das t-te Symbol wk ausgibt und in
den ( t+1)-ten Zustand, sj , übergeht, wenn der t-te
Zustand si war.
wk
p si
sj
=: p ( st+1 = sj , wt = wk | st = si )
= p ( sj, wk | si )
G.Heyer
16
Sprachprodukttechnologie SS 2001
Die Wahrscheinlichkeit einer Folge w1,n
lässt sich nunmehr berechnen als die Wahrscheinlichkeit aller
möglichen Pfade durch das HMM, das diese Folge generieren
könnte:
p (w1,n) =  p ( w1,n , s1,n+1 )
s1,n+1
G.Heyer
17
Sprachprodukttechnologie SS 2001
Ergänzende Literatur
E.Charniak, Statistical Language Learning, MIT Press:
Cambridge (Mass.) 1993
C. Manning und H.Schütze, Foundations of Statistical
Natural Language Processing, MIT Press: Cambridge (Mass.)
1999 (32000)
D.Juravsky, J.Martin, Speech and Language Processing: An
Introduction to Natural Language Processing, Computational
Linguistics and Speech Recognition, Prentice Hall: San
Francisco 2000
G.Heyer
18
Sprachprodukttechnologie SS 2001