§10 Winkel

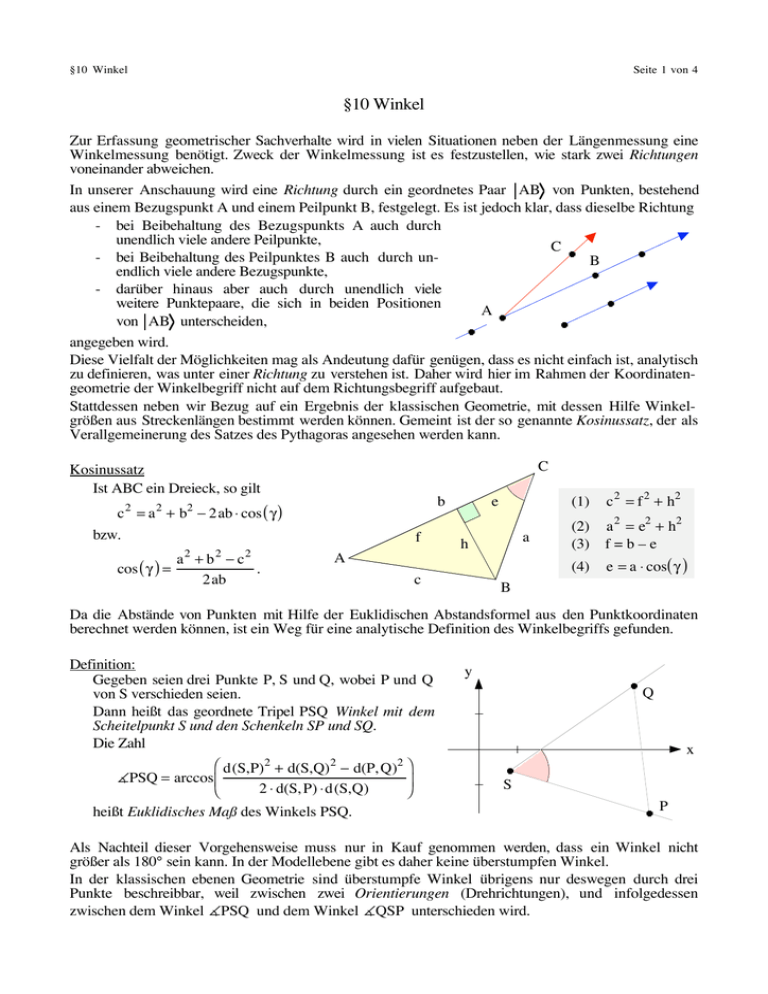
§10 Winkel
Seite 1 von 4
§10 Winkel
Zur Erfassung geometrischer Sachverhalte wird in vielen Situationen neben der Längenmessung eine
Winkelmessung benötigt. Zweck der Winkelmessung ist es festzustellen, wie stark zwei Richtungen
voneinander abweichen.
In unserer Anschauung wird eine Richtung durch ein geordnetes Paar AB von Punkten, bestehend
aus einem Bezugspunkt A und einem Peilpunkt B, festgelegt. Es ist jedoch klar, dass dieselbe Richtung
- bei Beibehaltung des Bezugspunkts A auch durch
unendlich viele andere Peilpunkte,
C
- bei Beibehaltung des Peilpunktes B auch durch unB
endlich viele andere Bezugspunkte,
- darüber hinaus aber auch durch unendlich viele
weitere Punktepaare, die sich in beiden Positionen
A
von AB unterscheiden,
angegeben wird.
Diese Vielfalt der Möglichkeiten mag als Andeutung dafür genügen, dass es nicht einfach ist, analytisch
zu definieren, was unter einer Richtung zu verstehen ist. Daher wird hier im Rahmen der Koordinatengeometrie der Winkelbegriff nicht auf dem Richtungsbegriff aufgebaut.
Stattdessen neben wir Bezug auf ein Ergebnis der klassischen Geometrie, mit dessen Hilfe Winkelgrößen aus Streckenlängen bestimmt werden können. Gemeint ist der so genannte Kosinussatz, der als
Verallgemeinerung des Satzes des Pythagoras angesehen werden kann.
C
Kosinussatz
Ist ABC ein Dreieck, so gilt
b
c = a + b − 2ab ⋅ cos ( γ )
bzw.
2
2
2
2
2
2
a +b −c
cos ( γ ) =
.
2ab
f
A
e
a
h
(1)
c 2 = f 2 + h2
(2)
(3)
a 2 = e2 + h2
f=b–e
(4)
c
e = a ⋅ cos( γ )
B
Da die Abstände von Punkten mit Hilfe der Euklidischen Abstandsformel aus den Punktkoordinaten
berechnet werden können, ist ein Weg für eine analytische Definition des Winkelbegriffs gefunden.
Definition:
Gegeben seien drei Punkte P, S und Q, wobei P und Q
von S verschieden seien.
Dann heißt das geordnete Tripel PSQ Winkel mit dem
Scheitelpunkt S und den Schenkeln SP und SQ.
Die Zahl
⎛ d(S,P) + d(S,Q) − d(P, Q)
PSQ = arccos ⎜
⎟
2 ⋅ d(S, P) ⋅d(S,Q)
⎝
⎠
heißt Euklidisches Maß des Winkels PSQ.
2
2
y
Q
x
2⎞
S
P
Als Nachteil dieser Vorgehensweise muss nur in Kauf genommen werden, dass ein Winkel nicht
größer als 180° sein kann. In der Modellebene gibt es daher keine überstumpfen Winkel.
In der klassischen ebenen Geometrie sind überstumpfe Winkel übrigens nur deswegen durch drei
Punkte beschreibbar, weil zwischen zwei Orientierungen (Drehrichtungen), und infolgedessen
zwischen dem Winkel PSQ und dem Winkel QSP unterschieden wird.
§10 Winkel
Seite 2 von 4
Anmerkungen:
Gegeben sei ein Punkt S sowie drei weitere
Punkte P, Q und R, die von S verschieden sind.
Dann gilt:
(a) PSQ = QSP
S
(b) Q ∈SP ⇔
[PSQ = 0°] ∨ [PSQ = 180°]
R
* (c) Von den drei Winkeln
PSQ , QSR , PSR
ist der größte die Summe der beiden
kleineren.
S
* (d) PSQ + QPS + SQP = 180°
Q
Q
P
S
P
Q
Q
P
S
P
Im Gegensatz zur Anmerkung (a) sind die Anmerkungen (b), (c) und (d), die ebenfalls anschaulich
offensichtliche Sachverhalte beschreiben, nur mit viel Aufwand zu beweisen!
Die Anmerkungen (2) und (3) sind von großer Bedeutung für die Definition des Schnittwinkels zweier
sich schneidender Geraden. Da eine Geradenkreuzung durch den Schittpunkt S und zwei weitere von S
verschiedene Punkte P1 und P2 , die auf den beiden Geraden liegen, geometrisch festgelegt ist, sollte
der Schnittwinkel der beiden Geraden mit Hilfe eines solchen Punktetripels bestimmt werden können.
Dieser Gedanke ist aber nur dann sinnvoll, wenn die
Größe des von den drei Punkten gebildete Winkels
g2
P1SP2 nicht von der Lage der Punkte auf den beiden
S
Geraden abhängt. Genau das drücken aber die AnmerP1
β
kungen (2) und (3) aus, auch wenn diese noch zulassen, g
1
dass sich bei einer Veränderung der Lage eines
α
P2
Geradenpunkts die Größe des Winkel P1SP2 in die
Größe des Supplementärwinkels (Ergänzungswinkel zu
180°) ändert.
Das wiederum stimmt aber mit den Erkenntnissen der klassischen Geometrie überein, in der ja auch
festgestellt wird, dass zwei sich schneidende Geraden insgesamt vier Winkel bilden, wobei Scheitelwinkel gleich groß und Nebenwinkel supplementär sind, d.h. sich zu 180° ergänzen. Deswegen wird in
der klassischen Geometrie verabredet, als Maß des Schnittwinkels die kleinere der beiden vorkommenden Winkelgrößen anzusehen.
Würde also in der analytischen Geometrie einfach (g1 ;g2 ) = P1SP2 definiert werden, wäre der
Schnittwinkel nicht eindeutig bestimmt; denn P1SP2 kann je nach Lage der Punkte der stumpfe
Winkel α oder der spitze Winkel β sein.
Andererseits folgt aus
β = 180° − α
sofort
cos (β ) = cos(180° − α ) = − cos (α )
und damit
cos (β ) = cos (α ) .
Das bedeutet aber, dass
cos ( (g1; g2 )) = cos(P1SP2 )
in jedem Fall richtig ist, und weil cos ( (g1;g 2 )) wegen 0° ≤ (g1 ;g2 ) ≤ 90° garantiert positiv ist,
können die Betragsstriche auf der linken Seite der Gleichung weggelassen werden:
cos ( (g1;g 2 )) = cos ( P1SP2 )
Diese Beziehung ist die Grundlage für die folgende Definition:
§10 Winkel
Seite 3 von 4
Definition
Gegeben seien zwei Geraden g1 und g 2 , die sich in einem Punkt S schneiden. Weiterhin seien P1
und P2 zwei von S verschiedene Punkte auf g1 bzw. g 2 . Dann heißt
⎛ d (S, P )2 + d (S,P )2 − d ( P ; P )2
1
2
1 2
(g1 ;g2 ) := arccos( cos(∠P1SP2 ) ) = arccos⎜
⎜⎝
2 ⋅d ( S,P1 ) ⋅ d ( S,P2 )
⎞
⎟
⎟⎠
Maß des Schnittwinkels der Geraden g1 und g 2 .
Wir zeigen nun im Folgenden, dass die Größe des Winkels zweier Geraden auch direkt mit Hilfe der
Koeffizienten ihrer Gleichungen bestimmt werden kann.
„Formel für den Schnittwinkel zweier Geraden“
Gegeben seien zwei Geraden g1 : a1 x + b1y = c1
Punkt S = S = (x S;y S ) schneiden. Dann gilt
und g 2 : a 2 x + b 2 y = c2 , die sich in einem
⎛
⎞
a1a 2 + b1 b2
 ( g1 ;g 2 ) = arccos ⎜
⎟.
⎜⎝ a 2 + b 2 a 2 + b 2 ⎟⎠
1
1
2
2
Beweis:
Wir betrachten die Punkte P1 = (x S + b1; yS − a1 ) und P2 = ( xS + b2 ; yS − a 2 ) .
Da nicht a 1 und b1 sowie a 2 und b 2 gleichzeitig verschwinden können, sind die beiden Punkte
garantiert von S verschieden. Es gilt:
P1 ∈g 1 ⇔ a 1 (xS + b1 ) + b1 (yS − a1 ) = c1
⇔ a 1xS + a1b1 + b1 yS − a 1b1 = c1 ⇔ a1xS + b1yS = c1
P2 ∈g2 ⇔ a 2 (x S + b 2 ) + b2 (y S − a 2 ) = c 2 ⇔ a 2 xS + b2 yS = c 2
Beide Aussagen sind wahr, weil S auf beiden Geraden liegt, und daher die Koordinaten von S beide
Geradengleichungen erfüllen müssen.
Die behauptete Formel ergibt sich nun dadurch, dass mit den so gewählten Punkten P1 , P2 und S
der Schnittwinkel gemäß der oben festgelegten Definitionsgleichung „ausgerechnet“ wird. Diese
Rechnung wird dem Leser als Übung 9.2 überlassen.
Für viele geometrische Aufgaben ist es, wie wir bereits gesehen haben, günstiger mit den Funktionsgleichungen der beteiligten Geraden zu arbeiten; deshalb notieren wir folgende Variante der Schnittwinkelformel, die sich direkt aus der allgemeinen Formel durch Einsetzen ergibt.
Satz
Gegeben seien zwei Geraden g1 : y = m1x + n1 und g 2 : y = m 2 x + n 2 . Dann gilt:
⎛
⎞
m 1m 2 + 1
∠ ( g1 ;g 2 ) = arccos ⎜
⎟
⎜⎝ m 2 + 1 m 2 + 1 ⎟⎠
1
2
§10 Winkel
Seite 4 von 4
Übungen zu §10
Übung 10.1 (vgl. Übung 3.1)
Gegeben ist das Viereck ABCD mit A = (–5; –4), B = (7; –2), C = (5; 6) und D = (–2; 5).
(a) Bestimme die Innenwinkel des Vierecks
(b) Bestimme mit Hilfe der Koeffizienten der zugehörigen Geradengleichungen die Winkel unter
denen sich die
- Diagonalen,
- benachbarten Seiten (vergleiche die Ergebnisse mit denen aus Teilaufgabe (a)) und
- gegenüberliegenden Seiten
schneiden.
Übung 10.2
Vervollständige den Beweis der Schnittwinkelformel für zwei Geraden; berechne dazu P1SP2 für
S = (x S;y S ) , P1 = (x S + b1; yS − a1 ) und P2 = ( xS + b2 ; yS − a 2 ) .
Übung 10.3
Untersuche allgemein, welche Werte die Schnittwinkelformel für parallele bzw. identische Geraden
liefert.
Übung 10.4
Gegeben seien zwei Punkte A = ( x A ;y A ) und B = (x B; yB ) . Bestimme den Winkel zwischen der
Geraden AB und der Symmetrieachse m AB .