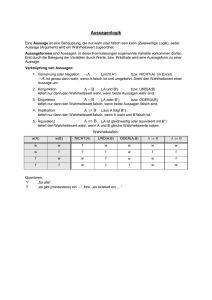
1.Logik und Mengen Aussagen als Bausteine der Logik beziehen

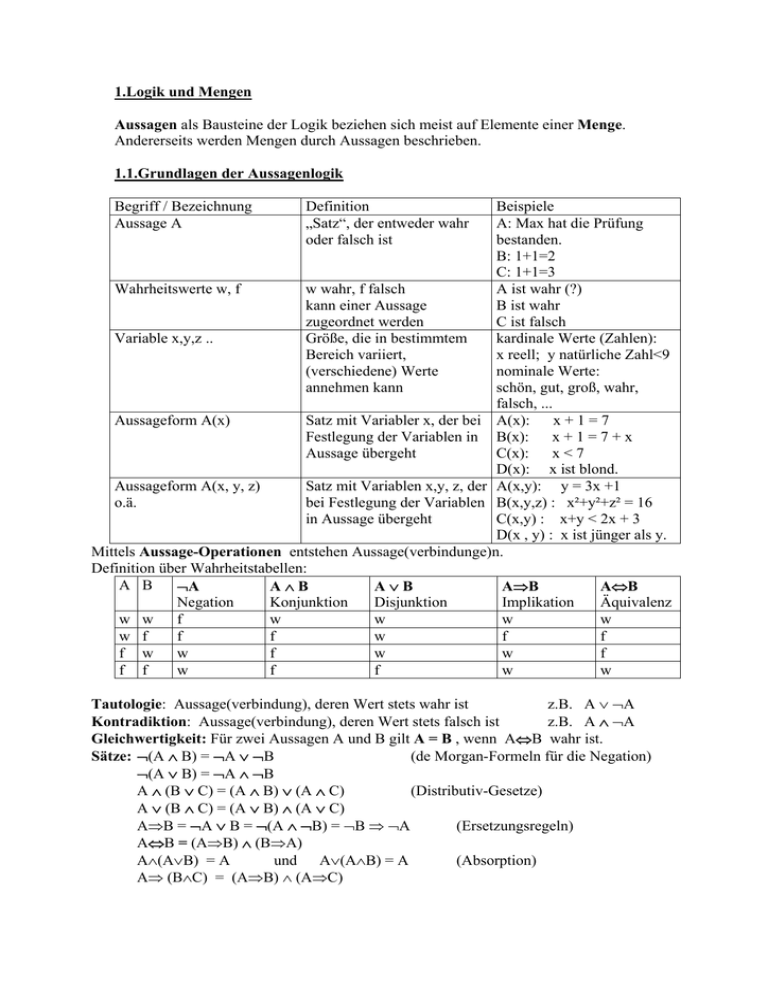
1.Logik und Mengen
Aussagen als Bausteine der Logik beziehen sich meist auf Elemente einer Menge.
Andererseits werden Mengen durch Aussagen beschrieben.
1.1.Grundlagen der Aussagenlogik
Begriff / Bezeichnung
Aussage A
Definition
„Satz“, der entweder wahr
oder falsch ist
Beispiele
A: Max hat die Prüfung
bestanden.
B: 1+1=2
C: 1+1=3
Wahrheitswerte w, f
w wahr, f falsch
A ist wahr (?)
kann einer Aussage
B ist wahr
zugeordnet werden
C ist falsch
Variable x,y,z ..
Größe, die in bestimmtem
kardinale Werte (Zahlen):
Bereich variiert,
x reell; y natürliche Zahl<9
(verschiedene) Werte
nominale Werte:
annehmen kann
schön, gut, groß, wahr,
falsch, ...
Aussageform A(x)
Satz mit Variabler x, der bei A(x):
x+1=7
Festlegung der Variablen in B(x):
x+1=7+x
Aussage übergeht
C(x): x < 7
D(x): x ist blond.
Aussageform A(x, y, z)
Satz mit Variablen x,y, z, der A(x,y): y = 3x +1
o.ä.
bei Festlegung der Variablen B(x,y,z) : x²+y²+z² = 16
in Aussage übergeht
C(x,y) : x+y < 2x + 3
D(x , y) : x ist jünger als y.
Mittels Aussage-Operationen entstehen Aussage(verbindunge)n.
Definition über Wahrheitstabellen:
A B
¬A
A∧B
A∨B
A⇒B
A⇔B
Negation
Konjunktion
Disjunktion
Implikation
Äquivalenz
w w
f
w
w
w
w
w f
f
f
w
f
f
f w
w
f
w
w
f
f f
w
f
f
w
w
Tautologie: Aussage(verbindung), deren Wert stets wahr ist
z.B. A ∨ ¬A
Kontradiktion: Aussage(verbindung), deren Wert stets falsch ist
z.B. A ∧ ¬A
Gleichwertigkeit: Für zwei Aussagen A und B gilt A = B , wenn A⇔B wahr ist.
Sätze: ¬(A ∧ B) = ¬A ∨ ¬B
(de Morgan-Formeln für die Negation)
¬(A ∨ B) = ¬A ∧ ¬B
A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C)
(Distributiv-Gesetze)
A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C)
A⇒B = ¬A ∨ B = ¬(A ∧ ¬B) = ¬B ⇒ ¬A
(Ersetzungsregeln)
A⇔B = (A⇒B) ∧ (B⇒A)
A∧(A∨B) = A
und A∨(A∧B) = A
(Absorption)
A⇒ (B∧C) = (A⇒B) ∧ (A⇒C)
1.2.Grundlagen der Mengenlehre
Menge: Zusammenfassung von bestimmten Objekten der Anschauung oder des Denkens zu
einem Ganzen
Element der Menge: eines dieser Objekte
x∈A „x ist Element der Menge A” , Negation: x∉A
Beschreibung:
• Angabe der Elemente: A= {a1 , a2 , .... , an} oder B = {b1 , b2 , .... }
• Angabe einer Grundmenge G und einer Eigenschaft (Aussageform H)
A = {a∈G: H(a)} oder A = {a∈G⏐ H(a)} oder A = {a ⏐ a∈G, H(a)}
oder kurz A = {a ⏐ H(a)} wenn G als bekannt vorausgesetzt
• zeichnerisch (Venn-Diagramm, eventuell im Koordinatensystem )
leere Menge: ∅ oder { } z. B. ∅ = {x∈G: x ≠ x}
⏐A⏐ Mächtigkeit der Menge A : Anzahl der Elemente von A
Vergleich von Mengen:
A ⊆ B „A ist Teilmenge von B“ : „x∈A ⇒ x∈B“ ist wahr
A = B „A und B sind identisch“: A ⊆ B ∧ B ⊆ A bzw. „x∈A ⇔ x∈B“ ist wahr
manchmal zusätzlich A ⊂ B „A ist echte Teilmenge von B“: A ⊆ B ∧ A≠B
Satz: Die leere Menge ist Teilmenge jeder Menge.
P(A) Potenzmenge von A : Menge aller Teilmengen von A
Mengenoperationen:
A ∪ B = {x∈G: (x∈A) ∨ (x∈B)} (Vereinigungsmenge)
A ∩ B = {x∈G: (x∈A) ∧ (x∈B)} (Durchschnittsmenge)
A und B heißen disjunkt, wenn A ∩ B = ∅
A \ B = {x∈G: (x∈A) ∧ (x∉B)} (Differenzmenge)
speziell für A = G (als bekannt vorausgesetzt) mit B ⊆ G :
¬B = G \ B = {x∈G: x∉B} (Komplementmenge von B in G)
auch Bezeichnung B statt ¬B
Regeln analog Aussagenlogik, z.B. ¬ (A ∪ B) = ¬A ∩ ¬B
¬ (A ∩ B) = ¬A ∪ ¬B
Produktmenge A1 × A2 × .... × An = { (a1, a2,...,an) : ai ∈Ai , i = 1,..,n }
(a1, a2,...,an) n-Tupel , für n =2 Paar
Rn speziell für A1=..=An = R
Paarmenge: A × B = {(a,b) : (a∈A) ∧ (b∈B)}
Gleichheit von Paaren: (a,b) = (c,d) ⇔ (a = c) ∧ (b = d)
Quantoren ∀ und ∃
∀x{x∈G:H(x)} " H(x) ist für alle Ersetzungen von x durch Elemente von G wahr“
∃x{x∈G:H(x)} " H(x) ist für mindestens ein x aus G wahr“
Für G = {x1, x2,..,xn} ist ∀x{x∈G:H(x)} = H(x1) ∧ H(x2) ∧ ..... ∧ H(xn)
und ∃x{x∈G:H(x)} = H(x1) ∨ H(x2) ∨ ..... ∨ H(xn).
Negation:
¬∀x{x∈G:H(x)} = ∃x{x∈G: ¬H(x)}
¬∃x{x∈G:H(x)} = ∀x{x∈G: ¬H(x)}
1.3 Menge der reellen Zahlen
Zahlenbereiche: Ν ⊆ Ζ ⊆ Q ⊆ R ⊆ C
Menge der natürlichen Zahlen N :
Zahlen dienen zum „Nummerieren“ und zum „(Ab)zählen“
„ Nachfolgerprinzip“ , n+ sei der Nachfolger von n (also n+ = n+1)
Peanosche Axiome:
(1) 0 ∈ N
(2) wenn n ∈ N, so ist n+ ∈ N
(3) n+ ≠ 0 für alle n ∈ N
(4) wenn n+ = m+ für n, m ∈ N, so ist n = m
(5) sei S ⊆ N . Wenn 0 ∈ S und aus n ∈ S folgt n+ ∈ S , so ist S = N
Prinzip der vollständigen Induktion :
Es sei A(n) eine Aussageform mit der Variablen n ∈ N, n ≥ k.
Wenn
1.) A(k) wahr (Induktionsbasis, Induktionsvoraussetzung) und
2.) „A(n) ⇒ A(n+1)“ wahr für n ∈ N, n ≥ k (Induktionsschritt)
so ist A(n) wahr für alle n ∈ N, n ≥ k
z.B. Beweis von 1 + 2 + ...+ n = 0,5 n (n+1) o. ä Formeln
Die Elemente einer n-elementigen Menge seien nummeriert.
Unter einer Permutation p versteht man die Anordnung der Elemente in einer bestimmten
Reihenfolge, dargestellt durch
⎛ 1 2 3 ... n ⎞
⎟⎟
p = ⎜⎜
⎝ p1 p 2 p3 ... pn ⎠
Anzahl der möglichen Permutationen von n Elementen = n!
wobei (n + 1)!= (n + 1) ⋅ n! mit 0!=1
ÆAnzahl der Möglichkeiten, k Elemente aus n Elementen auszuwählen
⎛ n⎞
n!
ohne Beachtung der Reihenfolge: ⎜⎜ ⎟⎟ =
für n ≥ k
⎝ k ⎠ k!⋅(n − k )!
Sprechweise „n über k“ oder „k aus n“
Æ binomischer Lehrsatz:
(a + b )n = ∑ ⎛⎜⎜ ⎞⎟⎟a k b n−k
k
n
n
k =0
⎝ ⎠
⎛ n + 1⎞ ⎛ n ⎞ ⎛ n ⎞
⎟⎟
⎟⎟ = ⎜⎜ ⎟⎟ + ⎜⎜
Pascalsches Dreieck: ⎜⎜
⎝ k + 1⎠ ⎝ k ⎠ ⎝ k + 1⎠
Menge der ganzen Zahlen Z
Division mit Rest:
∀t , z ∈ Ζ, t > 0 : ∃!n, r ∈ Ζ, z = n ⋅ t + r ,
mit t – Divisor, r – Rest
speziell für r=0:
tz
„t teilt z“,
0≤r <t
d.h. z = n ⋅ t mit passendem n
z ≡ z´mod t heißt t ( z − z´)
„z ist kongruent modulo t zu z´“
Das bedeutet, dass die Zahlen z und z´ bei der Division durch t den gleichen Rest r lassen.
Man bezeichnet [i ]t = {z ∈ Ζ / z ≡ i mod t} als Restklasse.
Diese Menge enthält alle Zahlen, die bei Division durch t den gleichen Rest wie i lassen.
Man gibt folglich Restklassen an, indem man sie durch ein Mengenelement, am besten durch
den Rest r, charakterisiert.
Die Menge aller zu einer festen ganzen Zahl t gehörenden Restklassen stellt eine Partition
t −1
Ζ = U[i]t
von Z dar:
t −1
wobei
i =0
I[i] = { }
t
i =0
In dieser Menge lassen sich mit Hilfe der gewöhnlichen Operationen * zwischen ganzen
Zahlen (Addition und Multiplikation) zwei Operationen mit Restklassen definieren.
[a]t * [b]t = [a * b]t
Man kann dann ganz analog mit diesen Restklassen rechnen (Restklassenarithmetik).
Hierbei ist es egal, ob man erst die Reste bildet (passende Zahlen zwischen 0 und t-1 sucht)
oder erst die Rechenoperationen durchführt.
Die Menge der Restklassen stellt einen Ring dar, da die Multiplikation nicht immer
umkehrbar ist, die Gruppeneigenschaften sind bzgl. der Addition erfüllt.
Zahlensystem: Ziff = { 0; 1; …; b-1} mit b ≥ 2 natürliche Zahl
Basis b und Menge der Ziffern
Æ ∀z ∈ Ν∃!k ∈ Ν, ak −1 ,..., a1 , a0 ∈ Ziff , ak −1 ≠ 0 mit
z = ak −1b k −1 + ... + a1b + a0
kurz: z = ak −1ak −2 ..a0
b
„ b – adische Zahlendarstellung“
b = 10 Dezimalsystem, b=2 Dualsystem, b=16 Hexadezimalsystem mit Verwendung von
Buchstaben A,B,.. anstelle der Ziffern 10, 11, 12, 13, 14
z.B. 7041⏐10 = 1101110000001⏐2 = 1B81⏐16
Addition, Multiplikation wie bekannt (incl. Vorzeichenregeln)
Division Æ Menge der rationalen Zahlen Q:
Es werden auch negative Exponenten von b zugelassen, mittels Komma getrennt.
n=
k −1
∑a b
i = −∞
i
i
(b – adische Darstellung von n)
kurz: ak-1 ak-2...a1 a0 , a-1 a-2 …⏐b
Menge der reellen Zahlen R
(a, b, c ∈ R)
Mit den Verknüpfungen Addition ( + ) und Multiplikation ( · ) stellt die Menge der reellen
Zahlen einen Körper dar:
• Abgeschlossenheit bzgl + und ·
• a+b=b+a
(Kommutativität)
a·b=b·a
• ( a + b ) + c = a + ( b + c ) (Assoziativität)
(a·b)·c=a·(b·c)
• a·(b+c)=a·b+a·c
(Distributivität)
• Existenz neutrales Element 0 für Addition, 1 für Multiplikation:
0 + a = a + 0 = a und 1 · a = a · 1 = a
• Existenz inverser Elemente:
Für jedes a ∈ R existiert ein bzgl. der Addition inverses Element (-a) ∈ R
a + (-a) = (-a) + a = 0
Für jedes a ∈ R mit a ≠ 0 existiert ein bzgl. der Multiplikation inverses Element
1 1
⎛1⎞
a⋅ = ⋅a =1
⎜ ⎟∈ R
a a
⎝a⎠
•
•
•
•
•
Eigenschaften der Anordnungsbeziehung ≤ bzw. ≥ in R:
a≤a
(Reflexivität)
Aus a ≤ b und b ≤ a folgt a = b
(Identität)
Aus a ≤ b und b ≤ c folgt a ≤ c
(Transitivität)
Aus a ≤ b folgt a + c ≤ b + c
(Monotonie der Addition)
Aus a ≤ b und c > 0 folgt a · c ≤ b · c
(Monotonie der Multiplikation)
Aus a ≤ b und c < 0 folgt a · c ≥ b · c
Aus a ≥ b und c < 0 folgt a · c ≤ b · c
spezielle Teilmengen reeller Zahlen sind die Intervalle:
offene Intervalle
(a;b) = {x / x ∈ R, a < x, x< b}
abgeschlossene Intervalle
[a;b] = {x / x ∈ R, a ≤ x, x≤ b} bzw. halboffene Intervalle
Betrag einer Zahl x:
⎧ x
⎪
x =⎨ 0
⎪− x
⎩
für
x>0
für
für
x=0
x<0
Angabe einer Lösungsmenge L ⊆ Gü = Gültigkeitsbereich (Definitionsbereich) ⊆ R
--> Rechnen mit (Un)gleichungen und Beträgen
1.4 Menge der komplexen Zahlen C
Lösung einer quadratischen Gleichung:
x ² − 6 x + 5 = 0 besitzt die reellen Lösungen x1=1 und x2 = 5
x ² − 6 x + 13 = 0 besitzt keine reellen Lösungen, aber die komplexen Zahlen
x1 = 3 + 2 j
und
x2 = 3 − 2 j
sind Lösungen der Gleichung
mit j =
− 1 (imaginäre Einheit)
C = {z / z = x + jy, x, y ∈ R} oder C = {z / z = x + iy, x, y ∈ R} mit i ² = j ² = −1
Rechenregeln analog denen in R unter Berücksichtigung von i ² = j ² = −1
Komplexe Zahlen z werden als Punkte in der Koordinatenebene (Gauß´sche Ebene)
veranschaulicht.
Normalform von z:
z = x + iy wird durch ein Paar (x,y)∈R×R definiert.
kurz: z = (x , y)
Interpretation von x,y als kartesische Koordinaten eines Punktes
Bezeichnungen dabei:
x = Re(z) „Realteil von z“
y = Im(z) „Imaginärteil von z“
|z| = x 2 + y 2 „Norm oder Betrag von z“
z* = x − i⋅y „konjugiert komplex zu z“
--> z⋅z* = |z|² =|z*|² .
Übergang zu Polarkoordinaten (r, α) liefert die trigonometrische bzw. exponentielle
Darstellung:
z = r⋅{cos(α) + i⋅sin(α)}= r ⋅eiα (Eulersche Formel)
kurz: z = r / α
Zusammenhang/Umrechnung:
x = Re(z) = r⋅cos(α)
⎧
r = |z|
⎪
⎛ Im z ⎞
arctan⎜
⎟
⎝ Re z ⎠
⎪
π
⎪
α = ⎨ sign(Im z ) ⋅
2
⎪
⎪arctan⎛⎜ Im z ⎞⎟ + π
⎪⎩
⎝ Re z ⎠
y = Im(z) = r⋅sin(α) .
für
Re z > 0
für
Re z = 0
für
Re z < 0
Jede komplexe Zahl z besitzt genau n verschiedene n-te Wurzeln n z . Man erhält diese,
indem man eine beliebige mit den n-ten Einheitswurzeln cos(360°/n) + i⋅sin(360°/n)
multipliziert.
Æ Polynome n-ten Grades ; Addition, Multiplikation, Division (mit Rest);
Polynome bilden einen Ring (Def. s.u.).
Hauptsatz der Algebra:
In der Menge C der komplexen Zahlen ist jedes Polynom n-ten Grades in ein Produkt von n
Linearfaktoren zerlegbar:
p(z) = an zn + an−1 zn−1 + ...... + a2 z² + a1 z + a0 = an ⋅ (z − z1 ) ⋅ (z − z2 ) ⋅ ....... ⋅ (z − zn ) .
Die zk sind die (möglicherweise komplexen) Nullstellen des Polynoms.
Sind die Koeffizienten ak des Polynoms reelle Zahlen, so treten die komplexen Nullstellen
paarweise auf, da mit jeder Nullstelle auch der konjugiert komplexe Wert eine Nullstelle ist.
z.B. x ² − 6 x + 13 = ( x − 3 + 2 j )( x − 3 − 2 j )
Die entsprechenden Linearfaktoren werden i.A. zu quadratischen Ausdrücken
zusammengefasst.
ÆAnwendung/Notwendigkeit der Faktorisierung z.B. bei der Partialbruchzerlegung (PBZ)
Definitionen von Gruppe und Ring
Menge M mit einer inneren Verknüpfung
(E) Existenz und Eindeutigkeit :
(A) Assoziatvität:
(N) neutrales Element :
(I) inverses Element:
(K) Kommutativität:
(Ip) Idempotenz :
Î Gruppe: Axiome EANI gelten, z.B. Zahlbereiche:
,
Î Abelsche Gruppe: Axiome EANIK , z.B. Restklassen
Menge mit zwei inneren Verknüpfungen:
Es existieren zwei innere Verknüpfungen, die gewöhnlich als Addition und Multiplikation
geschrieben werden, und folgende Axiome zur Verträglichkeit:
(I*) Existenz des inversen Elements bezüglich der multiplikativen Verknüpfung, mit
Ausnahme des neutralen Elements der additiven Verknüpfung.
.
(Dl)
.
(Dr)
.
(D) Distributivität: Dl und Dr.
(T) Wenn 0 das neutrale Element bzgl. + bezeichnet,
dann folgt aus a·b = 0 für alle a, b aus M , dass a = 0 oder b = 0.
(U) Die neutralen Elemente bezüglich der Verknüpfungen, 0 und 1, sind nicht gleich.
Î
Ring: Axiome EANIK bzgl. + , EA bzgl. · und D, z.B. Polynome
Î
Körper: Axiome EANIK bzgl. + , EANI*K bzgl. · und DTU, z.B. R oder C