Parallelschaltung von E12

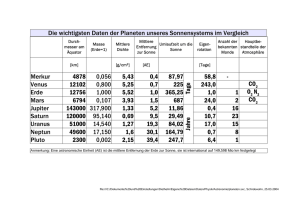
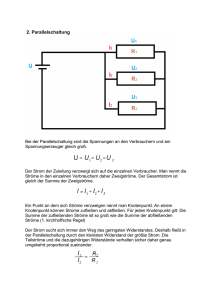
Parallelschaltung von Widerständen der Reihe E12
Parallelschaltung von Widerständen der Reihe E12
Problemstellung:
Es wird Ihnen in der Praxis öfters der Fall begegnen, dass Sie für eine Schaltung einen Widerstand
mit einem unüblichen Wert benötigen, aber nur E12 – Widerstände zur Verfügung haben. Dieses
Problem wird meist mit Parallelschaltung von Widerständen gelöst, eine Serienschaltung wird in der
Regel nur dann verwendet, wenn der zu bildende Widerstand sehr hochohmig ist.
R
R1
R2
Wie finde ich R1?
Wir wollen uns nun an einem Beispiel ansehen, wie wir zu den Widerstandswerten kommen.
Zuerst wollen wir für unsere Überlegungen den Widerstand R auftrennen in den Widerstand
Rsoll, den Widerstand, den wir uns wünschen, und Rist, den Widerstand, den wir durch die
Parallelschaltung wirklich erreichen konnten.
Rsoll
R1
R2
Rist
R1
R2
Natürlich ist es unser Ziel, die Parallelschaltung so zu dimensionieren, dass Rist dem Wert
von Rsoll möglichst nahe kommt.
Wenn wir z.B. einen Widerstand von 320 Ω benötigen, dann werden wir für R1 den
nächstgrößeren Wert der Reihe E12 verwenden, also 330Ω. Mit R2 müssen wir dann diesen
Wert soweit reduzieren, dass der Gesamtwiderstand Rist möglichst genau 320 Ω wird.
Wie finde ich R2?
Dazu müssen Sie
• R2 berechnen oder abschätzen
• mit den in der Nähe liegenden E12 – Werten probieren, welcher Wert für Ihre
Anwendung am besten passt
Berechnung von R2:
Aus der bekannten Formel
e12parallel.doc
1
1
1
=
+
R R1 R2
(1)
Seite 1/4
Vanek 2003.04.14
Parallelschaltung von Widerständen der Reihe E12
erhalten wir:
R2 =
1
1
1
−
Rsoll R1
1
=
1
1
−
320Ω 330Ω
= 10560Ω
Abschätzung von R2:
Wirkliche Profis berechnen R2 nicht sonder schätzen ihn nach der folgenden Methode ab
(das geht nach einiger Übung im Kopf):
Wenn wir bei gegebener Spannung einen Widerstand um 1% verkleinern, dann wird der
Strom um ca. 1% ansteigen. Das gleiche könnten wir erreichen, indem wir dem Widerstand
das hundertfache seines Wertes parallel schalten. Wollen wir den Widerstand um 2%
reduzieren, benötigen wir das 50 – fache, bei 3% das 33- fache, usw.
Reduktion von R1 in %
1
2
3
4
5
6
8
10
15
Ungefähre Größe von R2
100 · R1
50 · R1
33 · R1
25 · R1
20 · R1
17 · R1
13 · R1
10 · R1
7 · R1
Wollen wir 330 Ω auf 320 Ω reduzieren, dann ist das eine Reduktion von ungefähr 3%.
Daher müssen wir dem Widerstand ca. das 33 – fache seines Wertes parallel schalten, das
sind etwas mehr als 10 kΩ.
Benachbarte E12 - Werte ausprobieren:
Berechnung und Abschätzung haben sehr ähnliche Werte ergeben, beide etwas größer als
10 kΩ. Nun berechnen wir Rist mit den benachbarten E12 – Werten von R2:
Rist = R1 || R2 = 330Ω || 10kΩ = 319,46 Ω, Abweichung: -0,17%
Rist = R1 || R2 = 330Ω || 12kΩ = 321,17 Ω, Abweichung: +0,37%
R

rel. Abw. / % =  ist − 1 ⋅ 100
 Rsoll

Im Regelfall werden wir uns für jenen R2 entscheiden, der ein Rist liefert, das am nächsten an
Rsoll herankommt. In speziellen Fällen kann es auch unser Ziel sein, nur den nächst größeren
oder nur den nächst kleineren R2 zuzulassen, siehe Spannungsstabilisierung mit IC mit
einstellbarer Spannung.
In jedem Fall ist es sinnvoll, beide R2 zu bestimmen, jenen der das nächstgrößere Rist liefert
und jenen, der das nächstkleinere Rist liefert, und erst danach seine Wahl zu treffen.
e12parallel.doc
Seite 2/4
Vanek 2003.04.14
Parallelschaltung von Widerständen der Reihe E12
Geht es manchmal auch leichter?
Ja, manchmal gibt es eine Joker, und zwar immer dann, wenn R die Hälfte eines E12 –
Wertes beträgt.
Beispiele: 500 Ω = 1000 Ω || 1000 Ω
600 Ω = 1200 Ω || 1200 Ω
750 Ω = 1500 Ω || 1500 Ω, usw.
In so einem Fall ersparen Sie sich die ganze Rechnung.
Nur Übung macht den Meister!
In der Spalte R sind die Widerstandswerte eingetragen, die Sie erreichen sollen (Rsoll). In die
Spalten R1 und R2 tragen Sie die von ihnen gewählten E12 – Werte dieser Widerstände ein
und in die Spalte (R1||R2) den Wert von Rist. In die letzte Spalte tragen Sie die relative
Abweichung in % (einschließlich Vorzeichen) ein.
Wählen Sie R2 so, dass der Betrag der relativen Abweichung so klein wie möglich wird.
In den ersten beiden Zeilen finden Sie Beispiele.
R/Ω
R1 / Ω
R2 / Ω
(R1||R2) / Ω
Abweichung / %
320
730
45
1300
110
4900
21
330
820
10000
6800
319,46
731,76
-0,17
+0,24
Hinweis: Irgendwo ist ein Joker versteckt!
Zur Erinnerung: Reihe E12: 10, 12, 15, 18, 22, 27, 33, 39, 47, 56, 68, 82, 100, ...
Viel Erfolg!
e12parallel.doc
Seite 3/4
Vanek 2003.04.14
Parallelschaltung von Widerständen der Reihe E12
Lösung:
R/Ω
R1 / Ω
R2 / Ω
(R1||R2) / Ω
Abweichung / %
320
730
45
1300
110
4900
21
330
820
47
1500
220
5600
22
10000
6800
1000
10000
220
39000
470
319,46
731,76
44,89
1304,35
110,00
4896,86
21,02
-0,17
+0,24
-0,24
+0,33
+0,00
-0,06
+0,08
e12parallel.doc
Seite 4/4
Vanek 2003.04.14